Solución

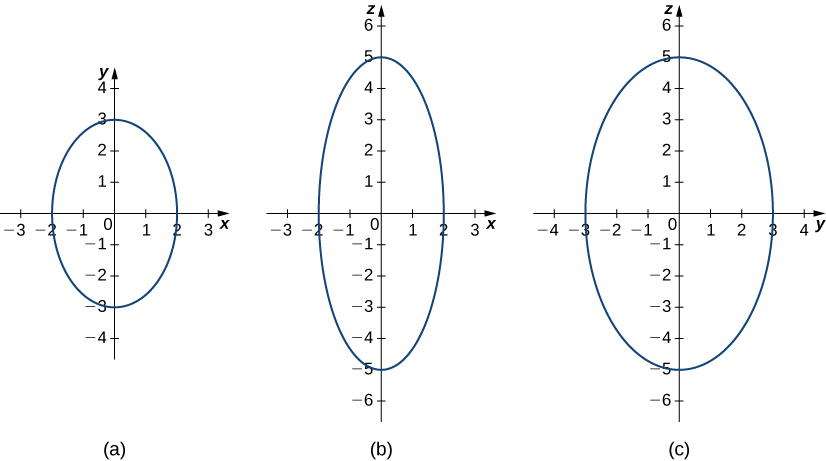
Comienza por dibujar las trazas. Para encontrar la traza en el plano $xy$, establece $z = 0: \frac{x^2}{2^2} + \frac{y^2}{3^2} = 1$ (consulta la Figura 2.81). Para encontrar los otros rastros, primero establece $y = 0$ y luego establece $x = 0$.

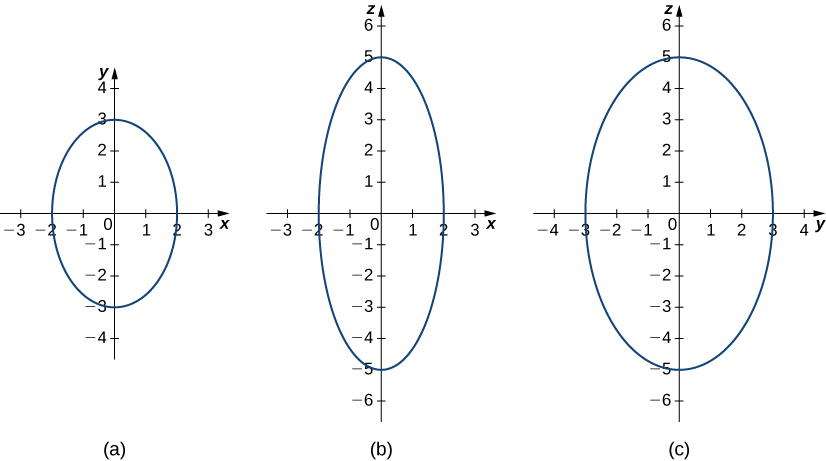
Figura 2.81. (a) Este gráfico representa la traza de la ecuación $\frac{x^2}{2^2} + \frac{y^2}{3^2} + \frac{z^2}{5^2} = 1$ en el plano $xy$, cuando establecemos $z = 0$. (b) Cuando establecemos $y = 0$, obtenemos la traza del elipsoide en el plano $xz$, que es una elipse. (c) Cuando establecemos $x = 0$, obtenemos la traza del elipsoide en el plano $yz$, que también es una elipse.

Ahora que sabemos cómo son las huellas de este sólido, podemos dibujar la superficie en tres dimensiones (Figura 2.82).

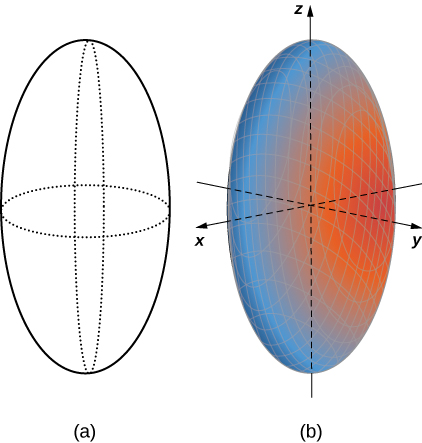
Figura 2.82. (a) Las trazas proporcionan un marco para la superficie. (b) El centro de este elipsoide es el origen.