Solución

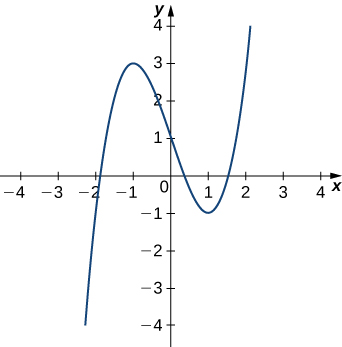
La figura 3.9 muestra la gráfica de $y = x^3−3x + 1$.

Figura 3.9. Queremos encontrar el círculo osculador de este gráfico en el punto donde $t = 1$.

Primero, calculemos la curvatura en $x = 1$:

Esto da $\kappa = 6$. Por lo tanto, el radio del círculo osculador está dado por $R = \frac{1}{\kappa} = \frac{1}{6}$. Luego, calculamos las coordenadas del centro del círculo. Cuando $x = 1$, la pendiente de la línea tangente es cero. Por lo tanto, el centro del círculo osculador está directamente encima del punto en el gráfico con coordenadas $(1, −1)$. El centro está ubicado en $(1, −\frac{5}{6})$. La fórmula para un círculo con radio $r$ y centro $(h, k)$ viene dada por $(x − h)^2+ (y − k)^2 = r^2$. Por lo tanto, la ecuación del círculo osculador es $(x − 1)^2+ (y + \frac{5}{6})^2 = \frac{1}{36}$. El gráfico y su círculo osculador aparecen en la siguiente figura.

Figura 3.10. El círculo osculador tiene radio $R = 1/6$.