Solución

Esta función es una función polinómica en dos variables. El dominio de ff consiste en pares de coordenadas (x,y)(x, y) que producen un beneficio no negativo:

16−(x−3)2−(y−2)2≥0(x−3)2+(y−2)2≤1616− (x − 3)^2− (y − 2)^2 \ge 0\\ (x − 3)^2+ (y − 2)^2 \le 16

Este es un disco de radio 44 centrado en (3,2)(3,2). Otra restricción es que ambos xx e yy no deben ser negativos. Cuando x=3x = 3 e y=2,f(x,y)=16y = 2, f (x, y) = 16. Ten en cuenta que es posible que cualquiera de los valores sea no entero. Por ejemplo, es posible vender 2.52.5 mil tuercas en un mes. El dominio, por lo tanto, contiene miles de puntos, por lo que podemos considerar todos los puntos dentro del disco. Para cualquier z<16z \lt 16, podemos resolver la ecuación f(x,y)=16f (x, y) = 16:

16−(x−3)2−(y−2)2=z(x−3)2+(y−2)2=16−z\begin{aligned} 16− (x − 3)^2− (y − 2)^2 &= z\\ (x − 3)^2+ (y − 2)^2 &= 16-z \end{aligned}

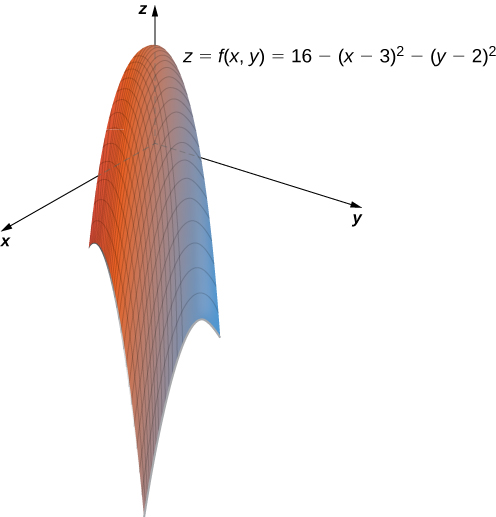
Como z<16z \lt 16, sabemos que 16−z>016 − z\gt 0, por lo que la ecuación anterior describe un círculo con radio 16−z\sqrt{16 − z} centrado en el punto (3,2)(3,2). Por lo tanto. el rango de f(x,y)f (x, y) es {z∈R∣z≤16}\{z\isin \Reals | z\le 16\}. La gráfica de f(x,y)f (x, y) también es un paraboloide, y este paraboloide apunta hacia abajo como se muestra a continuación.

Figura 4.6 El gráfico de la función dada de dos variables también es un paraboloide.