Solución

Apartado a

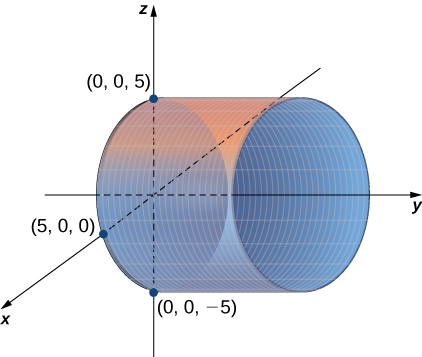
La variable $y$ puede tomar cualquier valor sin límite. Por lo tanto, las rectas que gobiernan esta superficie son paralelas al eje $y$. La intersección de esta superficie con el plano $xz$ forma un círculo centrado en el origen con radio $5$ (ver la siguiente figura).

Figura 2.77. La gráfica de la ecuación $x^2 + z^2 = 25$ es un cilindro con radio $5$ centrado en el eje $y$.

Apartado b

En este caso, la ecuación contiene las tres variables, $x, y$ y $z$, por lo que ninguna de las variables puede variar arbitrariamente. La forma más fácil de visualizar esta superficie es usar una utilidad de gráficos por computadora (consulta la siguiente figura).

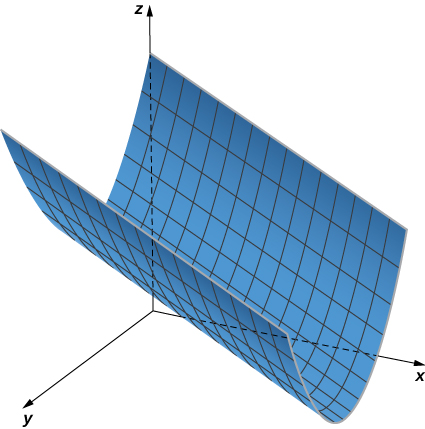
Figura 2.78. La gráfica de la ecuación $z = 2x^2 − y$.

Apartado c

En esta ecuación, la variable $z$ puede tomar cualquier valor sin límite. Por lo tanto, las rectas que componen esta superficie son paralelas al eje $z$. La intersección de esta superficie con los contornos del plano $xy$ es la curva $y = senx$ (ver la siguiente figura).

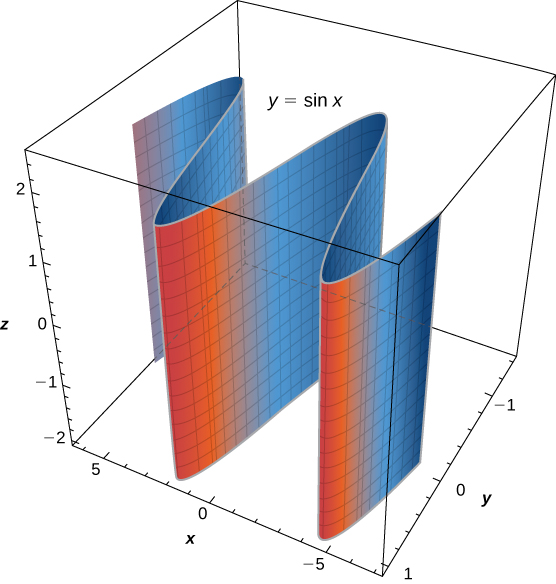
Figura 2.79. La gráfica de la ecuación $y = senx$ está formada por un conjunto de rectas paralelas al eje $z$ que pasan a través de la curva $y = senx$ en el plano $xy$.