Encontrando la derivada de una curva paramétrica

Apartado a

Para aplicar la ecuación, primero calcula x′(t)x'(t) e y′(t)y'(t):

x′(t)=2t,        y′(t)=2x'(t) = 2t, \;\;\;\;y'(t) = 2 dydx=dy/dtdx/dt=y′(t)x′(t)⇒dydx=22t⇒dydx=1t{{dy} \over {dx}} = {{dy/dt} \over {dx/dt}} = {{y'\left( t \right)} \over {x'\left( t \right)}}{\rm{ }} \Rightarrow {{dy} \over {dx}} = {2 \over {2t}} \Rightarrow {{dy} \over {dx}} = {1 \over t}

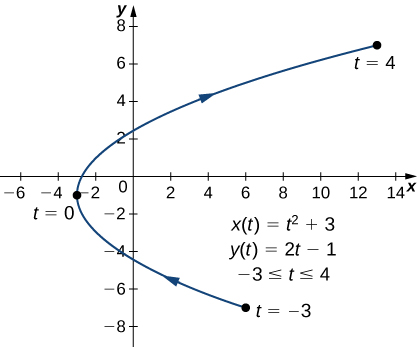
Figura. Gráfico de la curva descrita por ecuaciones paramétricas en la parte a.

Apartado b

Para aplicar la ecuación, primero calcula x′(t)x'(t) e y′(t)y'(t):

x′(t)=2        y′(t)=3t2−3x'(t) = 2 \;\;\;\;y'\left( t \right) = 3{t^2} - 3

Luego sustituye en la ecuación:

dydx=dy/dtdx/dt=y′(t)x′(t) ⇒dydx=3t2−32\frac{{dy}}{{dx}} = \frac{{dy/dt}}{{dx/dt}} = \frac{{y'\left( t \right)}}{{x'\left( t \right)}}{\text{ }} \Rightarrow \frac{{dy}}{{dx}} = \frac{{3{t^2} - 3}}{2}

Esta derivada es cero cuando t=±1t = ± 1.

Cuando t=−1t = −1 tenemos x(−1)=2⋅(−1)+1=−1x(−1) = 2\cdot(−1) + 1 = −1 y(−1)=(−1)3−3⋅(−1)+4=−1+3+4=6y\left( { - 1} \right) = {\left( { - 1} \right)^3} - 3 \cdot \left( { - 1} \right) + 4 = - 1 + 3 + 4 = 6,

que corresponde al punto (−1,6)(−1, 6) en la gráfica.

Cuando t=1t = 1 tenemos

x(1)=2⋅1+1=3x( 1) = 2 \cdot 1 + 1 = 3 y(1)=13−3⋅1+4=1−3+4=2y\left( 1 \right) = {1^3} - 3 \cdot 1 + 4 = 1 - 3 + 4 = 2

que corresponde al punto (3,2)(3, 2) en la gráfica. El punto (3,2)(3, 2) es un mínimo relativo y el punto (−1,6)(−1, 6) es un máximo relativo, como se ve en el siguiente gráfico.

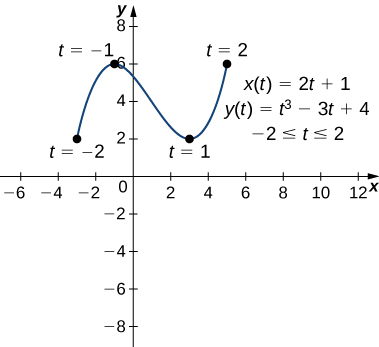
Figura. Gráfico de la curva descrita por ecuaciones paramétricas en la parte b.

Apartado c

Para aplicar la ecuación, primero calcula x′(t)x'(t) e y′(t)y'(t):

x′(t)=−5sent        y′(t)=5costx'(t) = - 5sent \;\;\;\;y'(t) = 5cost

Luego sustituye en la ecuación:

dydx=dy/dtdx/dt=y′(t)x′(t) ⇒dydx=5cos⁡t−5sent=−cot⁡ t\frac{{dy}}{{dx}} = \frac{{dy/dt}}{{dx/dt}} = \frac{{y'\left( t \right)}}{{x'\left( t \right)}}{\text{ }} \Rightarrow \frac{{dy}}{{dx}} = \frac{{5\cos t}}{{ - 5sent}} = - \cot \,t

Esta derivada es cero cuando cost=0cost = 0 y no está definida cuando sent=0sent = 0. Esto da t=0t = 0, π/2\pi/2, π\pi, 3π/23\pi/2 y 2π2\pi como puntos críticos para tt. Sustituyendo cada uno de ellos en x(t)x(t) e y(t)y(t), obtenemos

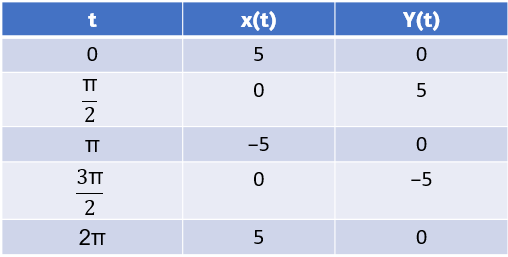
Estos puntos corresponden a los lados, arriba y abajo del círculo que se representa mediante las ecuaciones paramétricas (ver la siguiente figura). En los bordes izquierdo y derecho del círculo, la derivada no está definida, y en la parte superior e inferior, la derivada es igual a cero.

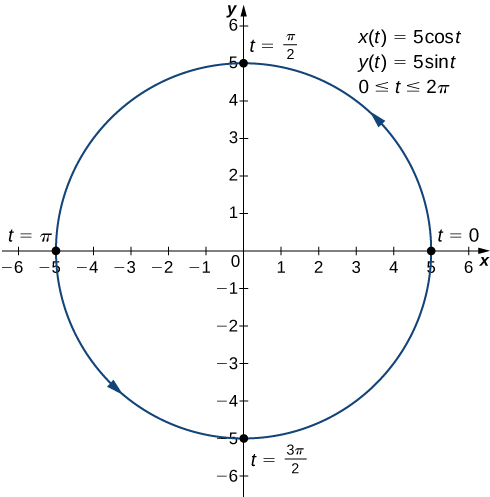
Figura. Gráfico de la curva descrita por ecuaciones paramétricas en la parte c.