Solución

La conversión de coordenadas cilíndricas a rectangulares requiere una aplicación simple de las ecuaciones enumeradas en el Teorema 2.15:

x=rcosθ=4cos2π3=−2y=rsenθ=4sin2π3=23z=z\begin{aligned} x &= rcos\theta=4cos\frac{2\pi}{3}=−2\\ y &= rsen\theta=4sin\frac{2\pi}{3}=2\sqrt{3}\\ z &= z \end{aligned}

El punto con coordenadas cilíndricas (4,2π3,−2)(4,\frac{2\pi}{3}, −2) tiene coordenadas rectangulares (−2,23,−2)(−2,2\sqrt{3}, −2) (ver la siguiente figura).

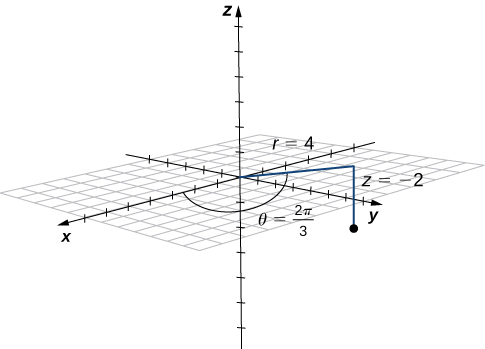
Figura 2.93. La proyección del punto en el plano xyxy es de 44 unidades desde el origen. La línea desde el origen hasta la proyección del punto forma un ángulo de 2π3\frac{2\pi}{3} con el eje xx positivo. El punto se encuentra 22 unidades debajo del plano xyxy.