Solución

Primero dibuje un gráfico que contenga ambas curvas como se muestra.

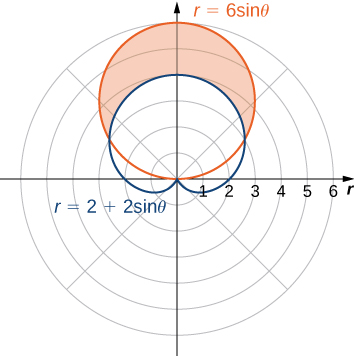
Figura 1.32 La región entre las curvas $r = 2 + 2sen\theta$ y $r = 6sen\theta$ .

Para determinar los límites de integración, primero encuentra los puntos de intersección estableciendo las dos funciones iguales entre sí y resolviendo para $\theta$ :

\begin{aligned} 6sen\theta &= 2 + 2sen\theta\\ 4sen\theta &= 2\\ sen\theta &= \frac12 \end{aligned}

Esto da las soluciones $\theta = \frac{\pi}{6}$ y $\theta = \frac{5\pi}{6}$ , que son los límites de la integración. El círculo $r = 3sen\theta$ es el gráfico rojo, que es la función externa, y el cardioide $r = 2 + 2sen\theta$ es el gráfico azul, que es la función interna. Para calcular el área entre las curvas, comienza con el área dentro del círculo entre $\theta = \frac{\pi}{6}$ y $\theta = \frac{5\pi}{6}$ , luego resta el área dentro del cardioide entre $\theta = \frac{\pi}{6}$ y $\theta = \frac{5\pi}{6}$ :

\begin{aligned} A &= \text{círculo - cardioide}\\ &= \frac12\int_{\pi/6}^{5\pi/6} (6sen\theta)^2d\theta - \frac12\int_{\pi/6}^{5\pi/6} (2 + 2sen\theta)^2d\theta\\ &= \frac12\int_{\pi/6}^{5\pi/6} 36sen^2\theta d\theta - \frac12\int_{\pi/6}^{5\pi/6} (4 + 8sen\theta + 4sen^2\theta)d\theta\\ &= 18\int_{\pi/6}^{5\pi/6}\frac{1-cos(2\theta)}{2}d\theta - 2\int_{\pi/6}^{5\pi/6} 1 + 2sen\theta + \frac{1-cos(2\theta)}{2}d\theta\\ &= 9\left[\theta - \frac{sen(2\theta)}{2}\right]_{\pi/6}^{5\pi/6} -2\left[\frac{3\theta}{2} -2cos\theta - \frac{sen(2\theta)}{4}\right]_{\pi/6}^{5\pi/6}\\ &= 9\left(\frac{5\pi}{6} - \frac{sen 2(5\pi/6)}{2}\right) - 9\left(\frac{\pi}{6} - \frac{sen 2(\pi/6)}{2}\right)\\ &= \left(3(\frac{5\pi}{6}) - 4cos\frac{5\pi}{6} - \frac{sen 2(5\pi/6)}{2}\right) + \left(3(\frac{\pi}{6}) - 4cos\frac{\pi}{6} - \frac{sen 2(\pi/6)}{2}\right)\\ &= 4\pi \approx 12.57 \end{aligned}