Solución

Tenemos

u×v=⟨(0+1),−(0−3),(0−6)⟩=⟨1,3,−6⟩\bold{u}\times\bold{v} = \lang (0+1),−(0−3),(0−6)\rang =\lang 1,3,−6\rang v×u=⟨(−1−0),−(3−0),(6−0)⟩=⟨−1,−3,6⟩\bold{v}\times\bold{u} = \lang (−1−0),−(3−0),(6−0)\rang =\lang −1,−3,6\rang

Vemos que, en este caso, u×v=−(v×u)\bold{u}\times\bold{v} = - (\bold{v}\times\bold{u}) (Figura 2.56). Probamos esto en general más adelante en esta sección.

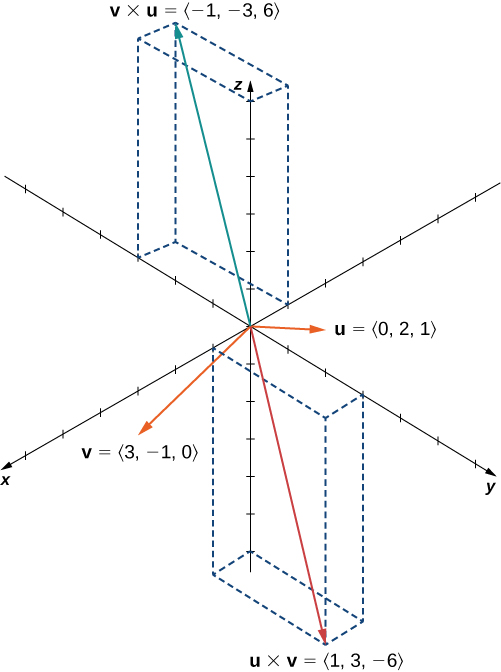
Figura 2.56. Los productos cruz u×v\bold{u}\times\bold{v} y v×u\bold{v}\times\bold{u} son ortogonales a u\bold{u} y v\bold{v}, pero en direcciones opuestas.