Solución

Apartado a

Utilizamos las ecuaciones 3.20, 3.21 y 3.22:

v(t)=r′(t)=2ti−t5−t2ja(t)=v′(t)=2i−5(5−t2)3/2jv(t)=∥r′(t)∥=(2t)2+(−t5−t2)2=4t2+t25−t2=21t2−4t45−t2\begin{aligned} \bold{v}(t) &= \bold{r^{\prime}}(t) = 2t\bold{i}-\frac{t}{\sqrt{5-t^2}}\bold{j}\\ \bold{a}(t) &= \bold{v^{\prime}}(t) = 2\bold{i}-5(5-t^2)^{3/2}\bold{j}\\ v(t) &= \|\bold{r^{\prime}}(t)\|\\ &= \sqrt{(2t)^2+\bigg(-\frac{t}{\sqrt{5-t^2}}\bigg)^2} \\ &= \sqrt{4t^2+\frac{t^2}{5-t^2}}\\ &= \sqrt{\frac{21t^2-4t^4}{5-t^2}} \end{aligned}

Apartado b

La gráfica de r(t)=t2i+5−t2j\bold{r}(t) = t^2\bold{i} + \sqrt{5 − t^2}\bold{j} es una porción de una parábola (Figura 3.11). El vector de velocidad en t=1est = 1 es

v(1)=r′(1)=2(1)i−15−12j=2i−12j\bold{v}(1)=\bold{r^{\prime}}(1)= 2(1)\bold{i}−\frac{1}{\sqrt{5-1^2}}\bold{j} = 2\bold{i}-\frac{1}{2}\bold{j}

y el vector de aceleración en t=1t = 1 es a(1)=v′(1)=2i−5(5−12)3/2j=2i−58j\bold{a}(1) = \bold{v^{\prime}}(1) = 2\bold{i}−5(5-1^2)^{3/2}\bold{j} = 2\bold{i}-\frac{5}{8}\bold{j}

Observa que el vector de velocidad es tangente a la ruta, como siempre es el caso.

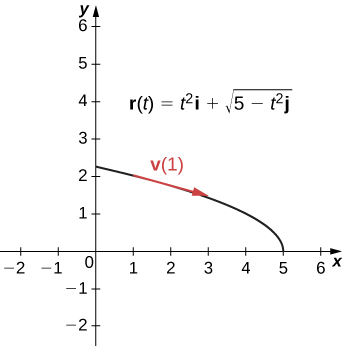
Figura 3.11. Este gráfico representa el vector de velocidad en el tiempo t=1t = 1 para una partícula que se mueve en una trayectoria parabólica.