Apartado a
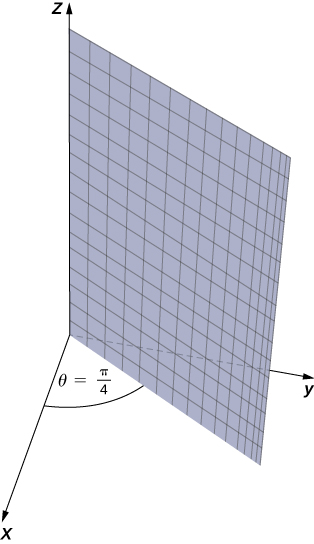
Cuando el ángulo se mantiene constante mientras y pueden variar, el resultado es un semiplano (ver la siguiente figura).

Figura 2.94. En coordenadas polares, la ecuación describe el rayo que se extiende diagonalmente a través del primer cuadrante. En tres dimensiones, esta misma ecuación describe un semiplano.
Apartado b
Sustituye en la ecuación para expresar la forma rectangular de la ecuación: . Esta ecuación describe una esfera centrada en el origen con radio (ver la siguiente figura).
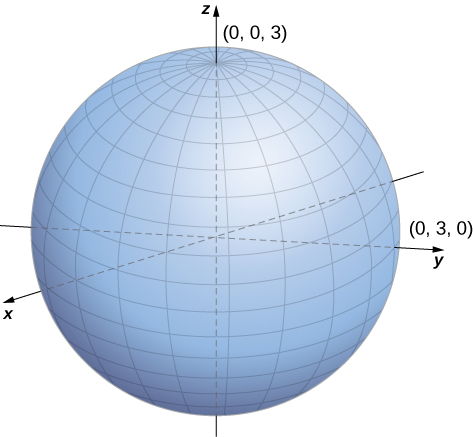
Figura 2.95. La esfera centrada en el origen con radio puede describirse mediante la ecuación cilíndrica .
Apartado c
Para describir la superficie definida por la ecuación , ¿es útil examinar trazas paralelas al plano ? Por ejemplo, la traza en el plano es el círculo , la traza en el plano es el círculo , y así sucesivamente. Cada traza es un círculo. A medida que aumenta el valor de , el radio del círculo también aumenta. La superficie resultante es un cono (ver la siguiente figura).
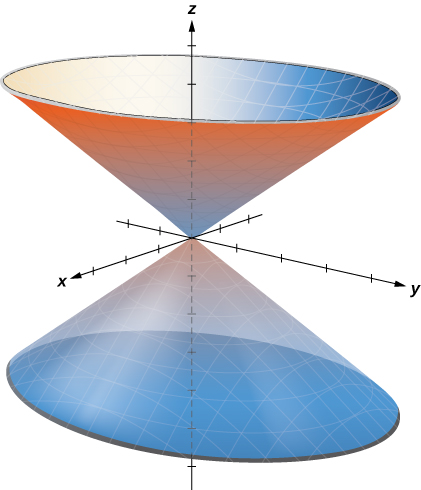
Figura 2.96. Las trazas en planos paralelos al plano son círculos. El radio de los círculos aumenta a medida que aumenta .