Solución

Apartado a

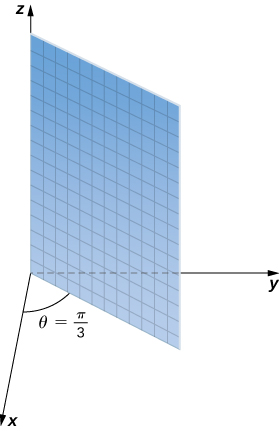
La variable θ\theta representa la medida del mismo ángulo en los sistemas de coordenadas cilíndricos y esféricos. Los puntos con coordenadas (ρ,π3,ϕ)(\rho, \frac{\pi}{3}, \phi) se encuentran en el plano que forma el ángulo θ=π3\theta=\frac{\pi}{3} con el eje xx positivo. Como ρ>0\rho\gt0, la superficie descrita por la ecuación θ=π3\theta=\frac{\pi}{3} es el semiplano que se muestra en la figura 2.101.

Figura 2.101. La superficie descrita por la ecuación θ=π3\theta=\frac{\pi}{3} es un semiplano.

Apartado b

La ecuación ϕ=5π6\phi = \frac{5\pi}{6} describe todos los puntos en el sistema de coordenadas esféricas que se encuentran en una línea desde el origen formando un ángulo que mide 5π6\frac{5\pi}{6} rad con el eje zz positivo. Estos puntos forman un medio cono (Figura 2.102). Debido a que solo hay un valor para ϕ\phi que se mide desde el eje zz positivo, no obtenemos el cono completo (con dos piezas)

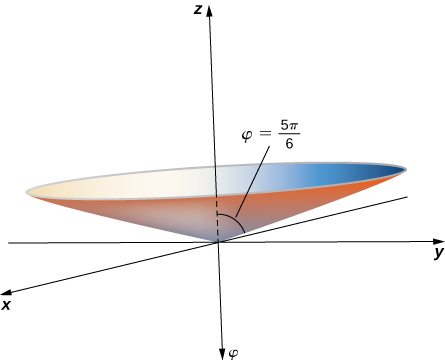
Figura 2.102. La ecuación ϕ=5π6\phi = \frac{5\pi}{6} describe un cono.

Para encontrar la ecuación en coordenadas rectangulares, use la ecuación ϕ=arccos(zx2+y2+z2)\phi = arccos (\frac{z}{\sqrt{x^2 + y^2 + z^2}})

5π6=arccos(zx2+y2+z2)cos5π6=zx2+y2+z2−32=zx2+y2+z234=z2x2+y2+z23x24+3y24+3z24=z23x24+3y24−z24=0\begin{aligned} \frac{5\pi}{6} &= arccos (\frac{z}{\sqrt{x^2 + y^2 + z^2}})\\ cos \frac{5\pi}{6} &= \frac{z}{\sqrt{x^2 + y^2 + z^2}}\\ -\frac{\sqrt{3}}{2} &= \frac{z}{\sqrt{x^2 + y^2 + z^2}}\\ \frac{3}{4} &= \frac{z^2}{x^2 + y^2 + z^2}\\ \frac{3x^2}{4} + \frac{3y^2}{4} + \frac{3z^2}{4} &= z^2\\ \frac{3x^2}{4} + \frac{3y^2}{4} - \frac{z^2}{4} &= 0 \end{aligned}

Esta es la ecuación de un cono centrado en el eje zz.

Apartado c

La ecuación ρ=6\rho = 6 describe el conjunto de todos los puntos a 66 unidades del origen: una esfera con radio 66 (Figura 2.103).

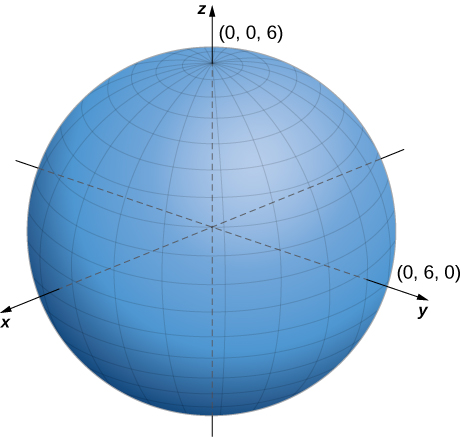
Figura 2.103. La ecuación ρ=6\rho = 6 describe una esfera con radio 66.

Apartado d

Para identificar esta superficie, convierta la ecuación de coordenadas esféricas a rectangulares, utilizando las ecuaciones y=ρsenϕsenθy = \rho sen \phi sen\theta y ρ2=x2+y2+z2\rho ^2 = x^2 + y^2 + z^2:

ρ=senθsenϕρ2=ρsenθsenϕx2+y2+z2=yx2+y2−y+14+z2=14x2+(y−12)2+z2=14\begin{aligned} \rho &= sen \theta sen\phi\\ \rho^2 &= \rho sen \theta sen\phi\\ x^2+y^2+z^2 &= y\\ x^2+y^2−y+\frac{1}{4}+z^2 &= \frac{1}{4}\\ x^2 + (y-\frac{1}{2})^2+z^2 &= \frac{1}{4} \end{aligned} Multiplica ambos lados de la ecuación por ρ\rho.
Sustituye las variables rectangulares usando las ecuaciones anteriores.
Sustracción de yy en ambos lados de la ecuación.
Completa el cuadrado.
Escribe los términos medios como un cuadrado perfecto.

La ecuación describe una esfera centrada en el punto (0,12,0)(0,\frac{1}{2},0) con radio 12\frac{1}{2}.