Solución

Primero, debemos calcular fx(x,y)f_x(x, y) y fy(x,y)f_y(x, y) , luego usa la ecuación 4.24 con x0=2x_0 = 2 y y0=−1y_0 = −1 :

fx(x,y)=4x−3y+2fy(x,y)=−3x+16y−4f(2,−1)=2(2)2−3(2)(−1)+8(−1)2+2(2)−4(−1)+4=34fx(2,−1)=4(2)−3(−1)+2=13fy(2,−1)=−3(2)+16(−1)−4=−26\begin{aligned} f_x(x, y) &= 4x − 3y + 2\\ f_y(x, y) &= −3x + 16y − 4\\ f(2, −1) &= 2(2)^2 − 3(2)(−1) + 8(−1)^2 + 2(2) − 4(−1) + 4 = 34\\ f_x(2, −1) &= 4(2) − 3(−1) + 2 = 13\\ f_y(2, −1) &= −3(2) + 16(−1) − 4 = −26 \end{aligned}

Entonces la ecuación 4.24 se convierte en

z=f(x0,y0)+fx(x0,y0)(x−x0)+fy(x0,y0)(y−y0)z=34+13(x−2)−26(y−(−1))z=34+13x−26−26y−26z=13x−26y−18.\begin{aligned} z &= f(x_0, y_0) + f_x(x_0, y_0)(x − x_0) + f_y(x_0, y_0)(y − y_0)\\ z &= 34 + 13(x − 2) − 26\big(y − (−1)\big)\\ z &= 34 + 13x − 26 − 26y − 26\\ z &= 13x − 26y − 18. \end{aligned}

(Ver la siguiente figura).

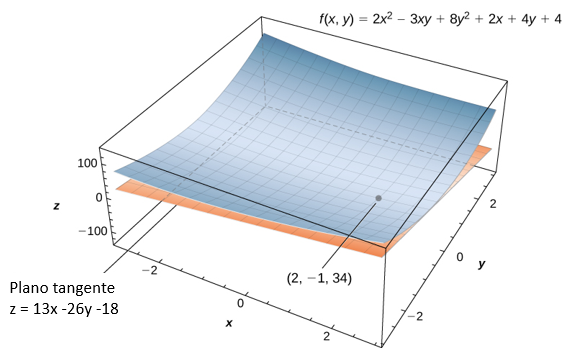
Figura 4.28 Cálculo de la ecuación de un plano tangente a una superficie dada en un punto dado.