Solución

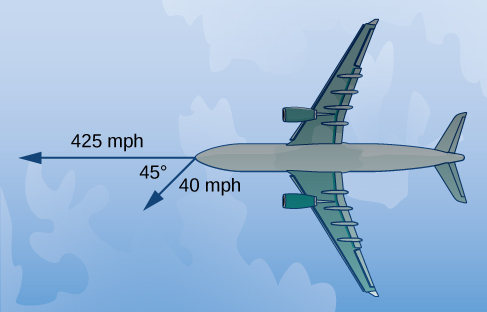
Comencemos dibujando la situación descrita (Figura 2.22).

Figura 2.22. Inicialmente, el avión viaja hacia el oeste. El viento es del noreste, por lo que sopla hacia el suroeste. El ángulo entre el rumbo del avión y el viento es de 45°. (Figura no dibujada a escala).

Configura un boceto para que los puntos iniciales de los vectores se encuentren en el origen. Entonces, el vector de velocidad del avión es p = −425i. El vector que describe el viento forma un ángulo de 225° con el eje x positivo:

w=⟨40cos(225o),40sen(225o)⟩=⟨−402,−402⟩=−402i−402j\bold{w} = \lang 40cos(225^o), 40sen(225^o)\rang = \bigg\lang -\frac{40}{\sqrt{2}}, -\frac{40}{\sqrt{2}}\bigg\rang = -\frac{40}{\sqrt{2}}\bold{i} -\frac{40}{\sqrt{2}}\bold{j}

Cuando la velocidad del aire y el viento actúan juntos en el avión, podemos sumar sus vectores para encontrar la fuerza resultante:

p+w=−425i+(−402i−402j)=(−425−402)i−402j\bold{p} + \bold{w} = −425\bold{i} + \bigg(-\frac{40}{\sqrt{2}}\bold{i} -\frac{40}{\sqrt{2}}\bold{j}\bigg) = \bigg(-425 - \frac{40}{\sqrt{2}}\bigg)\bold{i} - \frac{40}{\sqrt{2}}\bold{j}

La magnitud del vector resultante muestra el efecto del viento sobre la velocidad de avance del avión:

∥p+w∥=(−425−402)2+(−402)2≈454.17mph\| \bold{p} + \bold{w}\| = \sqrt{\bigg(-425 - \frac{40}{\sqrt{2}}\bigg)^2 + \bigg(- \frac{40}{\sqrt{2}}\bigg)^2} \approx 454.17 mph

Como resultado del viento, el avión viaja a aproximadamente 454 mph en relación con el suelo.

Para determinar el rumbo del avión, queremos encontrar la dirección del vector p + w:

tanθ=−402−425−402≈0.06tanθ = \frac{- \frac{40}{\sqrt{2}}}{-425 - \frac{40}{\sqrt{2}}} \approx 0.06 θ≈3.57o θ \approx 3.57^o

La dirección general del avión es 3.57° al suroeste.