Solución
Apartado a
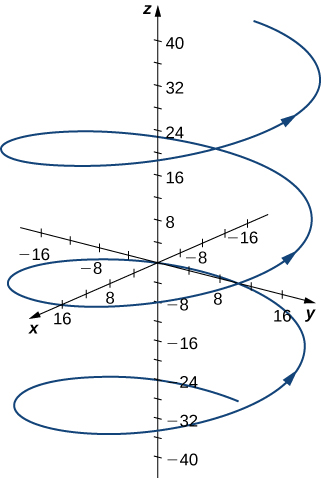
Esta función describe una hélice.
La curvatura de la hélice en t = ( 4 π ) / 3 t = (4\pi)/3 t = ( 4 π ) /3 T ( t ) \bold{T}(t) T ( t )
T ( t ) = r ′ ( t ) ∥ r ′ ( t ) ∥ = ⟨ − 4 s e n t , 4 c o s t , 3 ⟩ ( − 4 s e n t ) 2 + ( 4 c o s t ) 2 + 3 2 = ⟨ − 4 5 s e n t , 4 5 c o s t , 3 5 ⟩ \begin{aligned}
\bold{T}(t) &= \frac{\bold{r'}(t)}{\|\bold{r'}(t)\|}\\
&= \frac{\lang −4sent,4cost,3\rang}{\sqrt{(−4sent)^2+(4cost)^2+3^2}}\\
&= \bigg \lang −\frac{4}{5}sent,\frac{4}{5}cost,\frac{3}{5}\bigg\rang
\end{aligned} T ( t ) = ∥ r ′ ( t ) ∥ r ′ ( t ) = ( − 4 se n t ) 2 + ( 4 cos t ) 2 + 3 2 ⟨ − 4 se n t , 4 cos t , 3 ⟩ = ⟨ − 5 4 se n t , 5 4 cos t , 5 3 ⟩ A continuación, calcula T ′ ( t ) \bold{T'}(t) T ′ ( t )
T ′ ( t ) = ⟨ − 4 5 c o s t , − 4 5 s e n t , 0 ⟩ \bold{T'}(t) = \bigg \lang −\frac{4}{5}cost,−\frac{4}{5}sent,0\bigg\rang T ′ ( t ) = ⟨ − 5 4 cos t , − 5 4 se n t , 0 ⟩ Por último, aplica la ecuación 3.15:
κ = ∣ T ′ ( t ) ∥ ∣ r ′ ( t ) ∥ = ∥ ⟨ − 4 5 c o s t , − 4 5 s e n t , 0 ⟩ ∥ ∥ ⟨ − 4 s e n t , 4 c o s t , 3 ⟩ ∥ = ( − 4 5 c o s t ) 2 + ( − 4 5 s e n t ) 2 + 0 2 − 4 s e n t ) 2 + ( 4 c o s t ) 2 + 3 2 = 4 / 5 5 = 4 25 \begin{aligned}
\kappa &= \frac{|\bold{T'}(t)\|}{|\bold{r'}(t)\|} = \frac{\big\|\big \lang −\frac{4}{5}cost, −\frac{4}{5}sent,0\big\rang \big\|}{\|\lang −4sent,4cost,3\rang \|}\\
&= \frac{\sqrt{\big(−\frac{4}{5}cost\big)^2 + \big(−\frac{4}{5}sent\big)^2+0^2}}{\sqrt{−4sent)^2+(4cost)^2+3^2}}\\
&= \frac{4/5}{5} = \frac{4}{25}
\end{aligned} κ = ∣ r ′ ( t ) ∥ ∣ T ′ ( t ) ∥ = ∥ ⟨ − 4 se n t , 4 cos t , 3 ⟩ ∥ ∥ ∥ ⟨ − 5 4 cos t , − 5 4 se n t , 0 ⟩ ∥ ∥ = − 4 se n t ) 2 + ( 4 cos t ) 2 + 3 2 ( − 5 4 cos t ) 2 + ( − 5 4 se n t ) 2 + 0 2 = 5 4/5 = 25 4 La curvatura de esta hélice es constante en todos los puntos de la hélice.
Apartado b
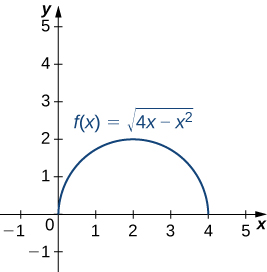
Esta función describe un semicírculo.
Para encontrar la curvatura de este gráfico, debemos usar la ecuación 3.16. Primero, calculamos y ′ y' y ′ y ′ ′ y'' y ′′
y = 4 x − x 2 = ( 4 x − x 2 ) 1 / 2 y ′ = 1 2 ( 4 x − x 2 ) − 1 / 2 ( 4 − 2 x ) = ( 2 − x ) ( 4 x − x 2 ) − 1 / 2 y ′ ′ = − ( 4 x − x 2 ) − 1 / 2 + ( 2 − x ) ( − 1 2 ) ( 4 x − x 2 ) − 3 / 2 ( 4 − 2 x ) = − 4 x − x 2 ( 4 x − x 2 ) 3 / 2 − ( 2 − x ) 2 ( 4 x − x 2 ) 3 / 2 = x 2 − 4 x − ( 4 − 4 x + x 2 ) ( 4 x − x 2 ) 3 / 2 = − 4 ( 4 x − x 2 ) 3 / 2 \begin{aligned}
y &= \sqrt{4x-x^2}=(4x−x^2)^{1/2}\\
y' &= \frac{1}{2}(4x−x^2)^{−1/2}(4−2x)=(2−x)(4x−x^2)^{−1/2}\\
y'' &= −(4x−x^2)^{−1/2}+(2−x)\big(−\frac{1}{2}\big)(4x−x^2)^{−3/2}(4−2x)\\
&= -\frac{4x-x^2}{(4x-x^2)^{3/2}}-\frac{(2-x)^2}{(4x-x^2)^{3/2}}\\
&= \frac{x^2-4x-(4-4x+x^2)}{(4x-x^2)^{3/2}}\\
&= -\frac{4}{(4x-x^2)^{3/2}}
\end{aligned} y y ′ y ′′ = 4 x − x 2 = ( 4 x − x 2 ) 1/2 = 2 1 ( 4 x − x 2 ) − 1/2 ( 4 − 2 x ) = ( 2 − x ) ( 4 x − x 2 ) − 1/2 = − ( 4 x − x 2 ) − 1/2 + ( 2 − x ) ( − 2 1 ) ( 4 x − x 2 ) − 3/2 ( 4 − 2 x ) = − ( 4 x − x 2 ) 3/2 4 x − x 2 − ( 4 x − x 2 ) 3/2 ( 2 − x ) 2 = ( 4 x − x 2 ) 3/2 x 2 − 4 x − ( 4 − 4 x + x 2 ) = − ( 4 x − x 2 ) 3/2 4 Luego, aplicamos la Ecuación 3.17:
κ = ∣ y ′ ′ ∣ [ 1 + ( y ′ ) 2 ] 3 / 2 = ∣ − 4 ( 4 x − x 2 ) 3 / 2 ∣ [ 1 + ( ( 2 − x ) ( 4 x − x 2 ) − 1 / 2 ) 2 ] 3 / 2 = ∣ 4 ( 4 x − x 2 ) 3 / 2 ∣ [ 1 + ( 2 − x ) 2 4 x − x 2 ] 3 / 2 = ∣ 4 ( 4 x − x 2 ) 3 / 2 ∣ [ 4 x − x 2 + x 2 − 4 x + 4 4 x − x 2 ] 3 / 2 = ∣ 4 ( 4 x − x 2 ) 3 / 2 ∣ ⋅ ( 4 x − x 2 ) 3 / 2 8 = 1 2 \begin{aligned}
\kappa &= \frac{|y''|}{[1+(y')^2]^{3/2}}\\
&= \frac{\bigg| -\frac{4}{(4x-x^2)^{3/2}}\bigg|}{\big[1+\big((2-x)\big(4x-x^2\big)^{-1/2}\big)^2\big]^{3/2}} = \frac{\bigg|\frac{4}{(4x-x^2)^{3/2}}\bigg|}{\bigg[1+\frac{(2-x)^2}{4x-x^2} \bigg]^{3/2}}\\
&= \frac{\bigg| \frac{4}{(4x-x^2)^{3/2}}\bigg|}{{\bigg[\frac{4x-x^2+x^2-4x+4}{4x-x^2}\bigg]^{3/2}}} = \bigg|\frac{4}{(4x-x^2)^{3/2}}\bigg| \cdot \frac{(4x-x^2)^{3/2}}{8}\\
&= \frac{1}{2}
\end{aligned} κ = [ 1 + ( y ′ ) 2 ] 3/2 ∣ y ′′ ∣ = [ 1 + ( ( 2 − x ) ( 4 x − x 2 ) − 1/2 ) 2 ] 3/2 ∣ ∣ − ( 4 x − x 2 ) 3/2 4 ∣ ∣ = [ 1 + 4 x − x 2 ( 2 − x ) 2 ] 3/2 ∣ ∣ ( 4 x − x 2 ) 3/2 4 ∣ ∣ = [ 4 x − x 2 4 x − x 2 + x 2 − 4 x + 4 ] 3/2 ∣ ∣ ( 4 x − x 2 ) 3/2 4 ∣ ∣ = ∣ ∣ ( 4 x − x 2 ) 3/2 4 ∣ ∣ ⋅ 8 ( 4 x − x 2 ) 3/2 = 2 1 La curvatura de este círculo es igual al recíproco de su radio. Hay un problema menor con el valor absoluto en la ecuación 3.16; sin embargo, una mirada más cercana al cálculo revela que el denominador es positivo para cualquier valor de x x x