Solución

Apartado a

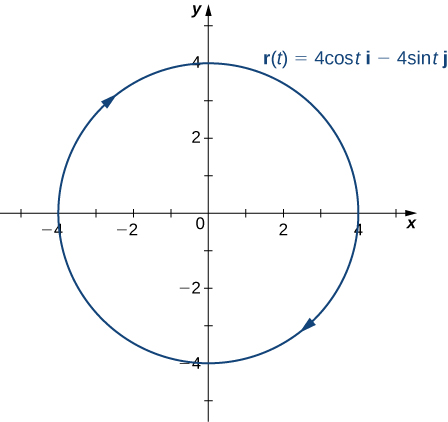
Esta función describe una circunferencia.

Para encontrar el vector normal principal unitario, primero debemos encontrarel vector tangente unitario T(t)\bold{T}(t):

T(t)=r′(t)∥r′(t)∥=−4senti−4costj(−4sent)2+(−4cost)2=−4senti−4costj16sen2t+16cos2t=−4senti−4costj16(sen2t+cos2t)=−4senti−4costj4=−senti−costj\begin{aligned} \bold{T}(t) &= \frac{\bold{r'}(t)}{\|\bold{r'}(t)\|}\\ &= \frac{-4sent\bold{i}-4cost\bold{j}}{\sqrt{(-4sent)^2+(-4cost)^2}}\\ &= \frac{-4sent\bold{i}-4cost\bold{j}}{\sqrt{16sen^2t+16cos^2t}}\\ &= \frac{-4sent\bold{i}-4cost\bold{j}}{\sqrt{16(sen^2t+cos^2t)}}\\ &= \frac{-4sent\bold{i}-4cost\bold{j}}{4}\\ &= -sent\bold{i}-cost\bold{j} \end{aligned}

A continuación, usamos la ecuación 3.18:

N(t)=T′(t)∥T′(t)∥=−costi+sentj(−cost)2+(sent)2=−costi+sentjsen2t+cos2t=−costi+sentj\begin{aligned} \bold{N}(t) &= \frac{\bold{T'}(t)}{\|\bold{T'}(t)\|}\\ &= \frac{-cost\bold{i}+sent\bold{j}}{\sqrt{(-cost)^2+(sent)^2}}\\ &= \frac{-cost\bold{i}+sent\bold{j}}{\sqrt{sen^2t+cos^2t}}\\ &= -cost\bold{i}+sent\bold{j} \end{aligned}

Observa que el vector tangente unitario y el vector normal principal unitario son ortogonales entre sí para todos los valores de tt:

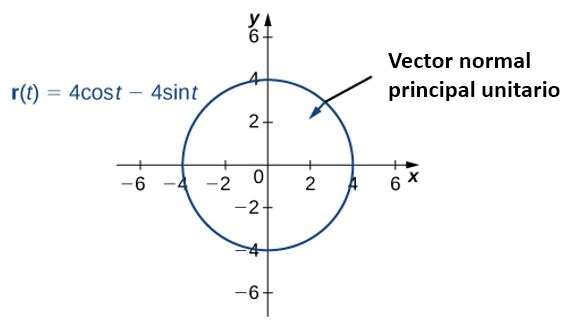
T(t)⋅N(t)=⟨−sent,−cost⟩⋅⟨−cost,sent⟩=sentcost−costsent=0\begin{aligned} \bold{T}(t)\cdot\bold{N}(t) &= \lang −sent,−cost\rang\cdot\lang −cost,sent\rang\\ &= sentcost−costsent\\ &= 0 \end{aligned}

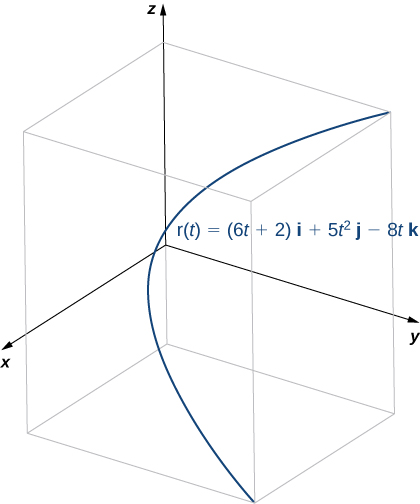
Además, el vector normal principal unitario apunta hacia el centro del círculo desde cada punto del círculo. Dado que r(t)\bold{r}(t) define una curva en dos dimensiones, no podemos calcular el vector binormal.

Apartado b

Esta función se ve así:

Para encontrar el vector normal principal unitario, primero debemos encontrarel vector tangente unitario T(t)\bold{T}(t):

T(t)=r′(t)∥r′(t)∥=6i+10tj−8k62+(10t)2+(−8)2=6i+10tj−8k36+100t2+64=6i+10tj−8k100(t2+1)=3i+5tj−4k5t2+1=35(t2+1)−1/2i−t(t2+1)−1/2j−45(t2+1)−1/2k\begin{aligned} \bold{T}(t) &= \frac{\bold{r'}(t)}{\|\bold{r'}(t)\|}\\ &= \frac{6\bold{i}+10t\bold{j}−8\bold{k}}{\sqrt{6^2+(10t)^2+(-8)^2}}\\ &= \frac{6\bold{i}+10t\bold{j}−8\bold{k}}{\sqrt{36+100t^2+64}}\\ &= \frac{6\bold{i}+10t\bold{j}−8\bold{k}}{\sqrt{100(t^2+1)}}\\ &= \frac{3\bold{i}+5t\bold{j}−4\bold{k}}{5\sqrt{t^2+1}}\\ &= \frac{3}{5}(t^2+1)^{-1/2}\bold{i} - t(t^2+1)^{-1/2}\bold{j} - \frac{4}{5}(t^2+1)^{-1/2}\bold{k} \end{aligned}

A continuación, calculamos T′(t)\bold{T}'(t) y ∥T′(t)∥\|\bold{T}'(t)\|:

T′(t)=35(−12)(t2+1)−3/2(2t)i+((t2+1)−1/2−t(12)(t2+1)−3/2(2t)j−45(−12)(t2+1)−3/2(2t)k=−3t5(t2+1)3/2i−1(t2+1)3/2j+4t5(t2+1)3/2k∥T′(t)∥=(−3t5(t2+1)3/2)2+(−1(t2+1)3/2)2+(4t5(t2+1)3/2)2=9t225(t2+1)3+1(t2+1)3+16t225(t2+1)3=25t2+2525(t2+1)3=1(t2+1)2=1t2+1\begin{aligned} \bold{T}'(t) &= \frac{3}{5}\big(-\frac{1}{2}\big)(t^2+1)^{-3/2}(2t)\bold{i} &+\bigg((t^2+1)^{-1/2} -t\big(\frac{1}{2}\big)(t^2+1)^{-3/2}(2t)\bold{j}\\ & -\frac{4}{5}\big(-\frac{1}{2}\big)(t^2+1)^{-3/2}(2t)\bold{k}\\ &= -\frac{3t}{5(t^2+1)^{3/2}}\bold{i} - \frac{1}{(t^2+1)^{3/2}}\bold{j} + \frac{4t}{5(t^2+1)^{3/2}}\bold{k}\\ \|\bold{T′}(t)\| &= \sqrt{\Bigg(-\frac{3t}{5(t^2+1)^{3/2}} \Bigg)^2 + \Bigg(- \frac{1}{(t^2+1)^{3/2}} \Bigg)^2 + \Bigg(\frac{4t}{5(t^2+1)^{3/2}} \Bigg)^2}\\ &= \sqrt{\frac{9t^2}{25(t^2+1)^3} + \frac{1}{(t^2+1)^3} + \frac{16t^2}{25(t^2+1)^3}}\\ &= \sqrt{\frac{25t^2+25}{25(t^2+1)^3}}\\ &= \sqrt{\frac{1}{(t^2+1)^2}}\\ &= \frac{1}{t^2+1} \end{aligned}

Por lo tanto, de acuerdo con la Ecuación 3.18:

N(t)=T′(t)∥T′(t)∥=(−3t5(t2+1)3/2i−1(t2+1)3/2j+4t5(t2+1)3/2k)(t2+1)=−3t5(t2+1)1/2i−55(t2+1)1/2j+4t5(t2+1)1/2k=−3ti+5j−4tk5t2+1\begin{aligned} \bold{N}(t) &= \frac{\bold{T'}(t)}{\|\bold{T'}(t)\|}\\ &= \Bigg(-\frac{3t}{5(t^2+1)^{3/2}}\bold{i} - \frac{1}{(t^2+1)^{3/2}}\bold{j} + \frac{4t}{5(t^2+1)^{3/2}}\bold{k}\Bigg)(t^2+1)\\ &= -\frac{3t}{5(t^2+1)^{1/2}}\bold{i} - \frac{5}{5(t^2+1)^{1/2}}\bold{j} +\frac{4t}{5(t^2+1)^{1/2}}\bold{k}\\ &= -\frac{3t\bold{i}+5\bold{j}−4t\bold{k}}{5\sqrt{t^2+1}} \end{aligned}

Una vez más, el vector tangente unitario y el vector normal principal unitario son ortogonales entre sí para todos los valores de tt:

T(t)⋅N(t)=(3i−5tj−4k5t2+1)⋅(−3ti+5j−4tk5t2+1)=3(−3t)−5t(−5)−4(4t)25(t2+1)=−9t+25t−16t25(t2+1)=0\begin{aligned} \bold{T}(t)\cdot\bold{N}(t) &= \bigg(\frac{3\bold{i}−5t\bold{j}−4\bold{k}}{5\sqrt{t^2+1}}\bigg)\cdot\bigg(-\frac{3t\bold{i}+5\bold{j}−4t\bold{k}}{5\sqrt{t^2+1}}\bigg)\\ &= \frac{3(−3t)−5t(−5)−4(4t)}{25\big(t^2+1\big)}\\ &= \frac{−9t+25t−16t}{25\big(t^2+1\big)}\\ &= 0 \end{aligned}

Por último, dado que r(t)\bold{r}(t) representa una curva tridimensional, podemos calcular el vector binormal utilizando la Ecuación 3.17:

B(t)=T(t)×N(t)=∣ijk35t2+1−5t5t2+1−45t2+1−3t5t2+1−55t2+14t5t2+1∣=((−5t5t2+1)(4t5t2+1)−(−45t2+1)(−55t2+1))i        −((35t2+1)(4t5t2+1)−(−45t2+1)(−3t5t2+1))j        +((35t2+1)(−55t2+1)−(−5t5t2+1)(−3t5t2+1))k=(−20t2−2025(t2+1))i+(−15−15t225(t2+1))k=−20(t2+125(t2+1))i−15(t2+125(t2+1))k=−45i−35k\begin{aligned} \bold{B}(t) &= \bold{T}(t)\times\bold{N}(t)\\ &= \begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\ \\ \frac{3}{5\sqrt{t^2+1}} & -\frac{5t}{5\sqrt{t^2+1}} & -\frac{4}{5\sqrt{t^2+1}}\\ \\ -\frac{3t}{5\sqrt{t^2+1}} & -\frac{5}{5\sqrt{t^2+1}} & \frac{4t}{5\sqrt{t^2+1}} \end{vmatrix}\\ &= \Bigg(\bigg(-\frac{5t}{5\sqrt{t^2+1}}\bigg)\bigg(\frac{4t}{5\sqrt{t^2+1}}\bigg) - \bigg(-\frac{4}{5\sqrt{t^2+1}}\bigg)\bigg(-\frac{5}{5\sqrt{t^2+1}}\bigg)\Bigg)\bold{i}\\ & \;\;\;\;-\Bigg(\bigg(\frac{3}{5\sqrt{t^2+1}}\bigg)\bigg(\frac{4t}{5\sqrt{t^2+1}}\bigg) - \bigg(-\frac{4}{5\sqrt{t^2+1}}\bigg)\bigg(-\frac{3t}{5\sqrt{t^2+1}}\bigg)\Bigg)\bold{j}\\ & \;\;\;\; +\Bigg(\bigg(\frac{3}{5\sqrt{t^2+1}}\bigg)\bigg(-\frac{5}{5\sqrt{t^2+1}}\bigg) - \bigg(-\frac{5t}{5\sqrt{t^2+1}}\bigg)\bigg(-\frac{3t}{5\sqrt{t^2+1}}\bigg)\Bigg)\bold{k}\\ &= \bigg(\frac{-20t^2-20}{25(t^2+1)}\bigg)\bold{i} +\bigg(\frac{-15-15t^2}{25(t^2+1)}\bigg)\bold{k}\\ &= -20\bigg(\frac{t^2+1}{25(t^2+1)}\bigg)\bold{i} -15\bigg(\frac{t^2+1}{25(t^2+1)}\bigg)\bold{k}\\ &= -\frac{4}{5}\bold{i} - \frac{3}{5}\bold{k} \end{aligned}