Solución

Apartado a

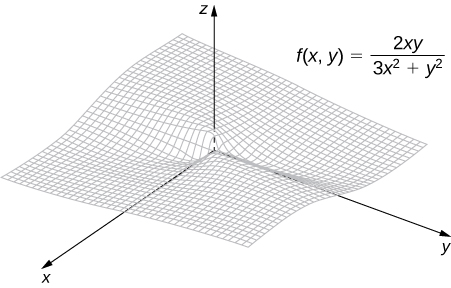
El dominio de la función $f (x, y) = \frac{2xy}{3x^2+y^2}$ consta de todos los puntos en el plano $xy$ , excepto el punto $(0,0)$ (Figura 4.16). Para mostrar que el límite no existe cuando $(x, y)$ se acerca $(0,0)$ , observamos que es imposible satisfacer la definición de un límite de una función de dos variables debido al hecho de que la función toma valores diferentes a lo largo de diferentes líneas que pasan por el punto $(0,0)$ . Primero, considera la línea $y = 0$ en el plano $xy$ . Sustituyendo $y = 0$ en $f (x, y)$ da

f(x,0) = \frac{2x(0)}{3x^2+0^2} = 0

para cualquier valor de $x$ . Por lo tanto, el valor de $f$ permanece constante para cualquier punto en el eje $x$ , y cuando $y$ se acerca a cero, la función permanece fija en cero.

Luego, considera la línea $y = x$ . Sustituyendo $y = x$ en $f (x, y)$ , obtenemos:

f(x,x) = \frac{2x(x)}{3x^2+x^2} = \frac{2x^2}{4x^2}=\frac{1}{2}

Esto es cierto para cualquier punto en la línea $y = x$ . Si dejamos que $x$ se acerque a cero mientras permanecemos en esta línea, el valor de la función permanece fijo en $1/2$ , independientemente de cuán pequeño sea $x$ .

Elige un valor para $\epsilon$ que sea menor que $1/2$ , digamos $1/4$ . Entonces, no importa cuán pequeño sea el disco $\delta$ que dibujemos alrededor de $(0,0)$ , los valores de $f (x, y)$ para los puntos dentro de ese disco $\delta$ incluirán tanto $0$ como $\frac{1}{2}$ . Por lo tanto, la definición de límite en un punto es nunca satisfecho y el límite no existe.

Figura 4.16 Gráfico de la función $f (x, y) = (2xy) / (3x^2 + y^2)$ . A lo largo de la línea $y = 0$ , la función es igual a cero; a lo largo de la línea $y = x$ , la función es igual a $\frac{1}{2}$ .

Apartado b

De manera similar al apartado anterior, Podemos acercarnos al origen a lo largo de cualquier línea recta que pase por el origen. Si probamos el eje $x$ (es decir, $y = 0$ ), la función permanece fija en cero. Lo mismo es cierto para el eje $y$ . Supongamos que nos acercamos al origen a lo largo de una línea recta de pendiente $k$ . La ecuación de esta línea es $y = kx$ . Entonces el límite se convierte

\begin{aligned} \lim\limits_{(x, y) \to (0, 0)}\frac{4xy^2}{x^2+3y^4} &= \lim\limits_{(x, y) \to (0, 0)}\frac{4x(kx)^2}{x^2+3(kx)^4}\\ &= \lim\limits_{(x, y) \to (0, 0)}\frac{4k^2x^3}{x^2+3k^4x^4}\\ &= \lim\limits_{(x, y) \to (0, 0)}\frac{4k^2x}{1+3k^4x^2}\\ &= \frac{\lim\limits_{(x, y) \to (0, 0)}4k^2x}{\lim\limits_{(x, y) \to (0, 0)}1+3k^4x^2}\\ &=0 \end{aligned}

independientemente del valor de $k$ . Parece que el límite es igual a cero. ¿Qué pasa si elegimos una curva que pasa por el origen? Por ejemplo, podemos considerar la parábola dada por la ecuación $x = y^2$ . Sustituyendo $y^2$ en lugar de $x$ en $f (x, y)$ da

\begin{aligned} \lim\limits_{(x, y) \to (0, 0)}\frac{4xy^2}{x^2+3y^4} &= \lim\limits_{(x, y) \to (0, 0)}\frac{4(y^2)y^2}{(y^2)^2+3y^4}\\ &= \lim\limits_{(x, y) \to (0, 0)}\frac{4y^4}{y^4+3y^4}\\ &= \lim\limits_{(x, y) \to (0, 0)} 1\\ &= 1 \end{aligned}

Por la misma lógica utilizadda en el apartado a, es imposible encontrar un disco $\delta$ alrededor del origen que satisfaga la definición del límite para cualquier valor de $\epsilon \lt 1$ . Por lo tanto, $\lim\limits_{(x, y) \to (0, 0)}\frac{4xy^2}{x^2+3y^4}$ no existe.