Cálculo de la recta tangente
Primero encuentra la pendiente de la línea tangente usando la ecuación, lo que significa calcular x′(t) e y′(t):
x′(t)=2ty′(t)=2
Luego sustituye en la ecuación:
dxdy=dx/dtdy/dt=x′(t)y′(t)⇒dxdy=2t2=t1
Cuando t=2, dxdy=21, entonces esta es la pendiente de la línea tangente.
Calculando x(2) y y(2), obtenemos:
x(2)=22−3=1y(2)=2⋅2−1=3
que corresponde al punto (1,3) en el gráfico (ver Figura abajo). Ahora usa la forma punto-pendiente de la ecuación de una línea para encontrar la ecuación de la línea tangente:
y−yo=m(x−xo)
y−3=21(x−1)
y=21x+25
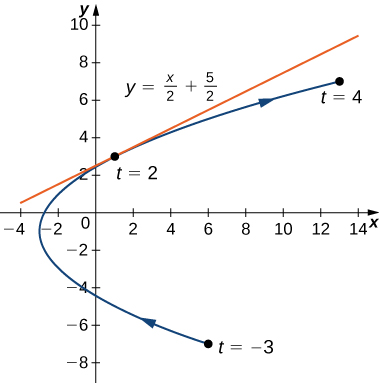
Figura. Línea tangente a la parábola descrita por las ecuaciones paramétricas dadas cuando t=2.

