Solución

Apartado a

Este es un ejemplo de una función lineal en dos variables. No hay valores o combinaciones de $x$ e $y$ que causen que $f (x, y)$ no esté definida, por lo que el dominio de $f$ es $\Reals^2$. Para determinar el rango, primero elige un valor para $z$. Necesitamos encontrar una solución a la ecuación $f (x, y) = z$, o $3x − 5y + 2 = z$. Una de esas soluciones se puede obtener estableciendo primero $y = 0$, que produce la ecuación $3x + 2 = z$. La solución a esta ecuación es $x = \frac{z − 2}{3}$, que da el par ordenado $(\frac{z − 2}{3},0)$ como una solución a la ecuación $f (x, y) = z$ para cualquier valor de $z$. Por lo tanto, el rango de la función es todos los números reales, o $\Reals$.

Apartado b

Para que la función $g (x, y)$ tenga un valor real, la cantidad debajo de la raíz cuadrada no debe ser negativa:

Esta desigualdad se puede escribir en la forma

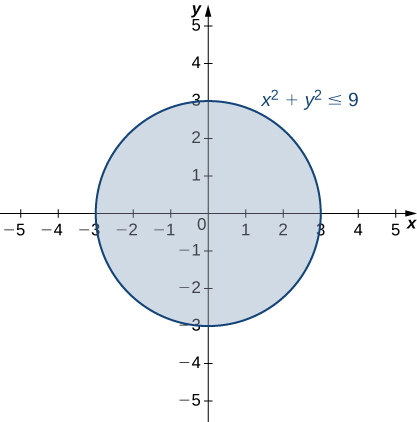
Por lo tanto, el dominio de $g (x, y)$ es $\{(x, y) \isin \Reals^2|x^2 + y^2\le 9\}$. El gráfico de este conjunto de puntos puede describirse como un disco de radio $3$ centrado en el origen. El dominio incluye el círculo límite como se muestra en el siguiente gráfico.

Figura 4.3 El dominio de la función $g (x, y) = \sqrt{9 − x^2 − y^2}$ es un disco cerrado de radio $3$.

Para determinar el rango de $g (x, y) = \sqrt{9 − x^2 − y^2}$ comenzamos con un punto $(x_0, y_0)$ en el límite del dominio, que se define por la relación $x^2 + y^2 = 9$. Se deduce que $x_0^2 + y_0^2 = 9$ y

Si $x_0^2 + y_0^2 = 0$ (en otras palabras, $x_0 = y_0 = 0$), entonces

Este es el valor máximo de la función. Dado cualquier valor $c$ entre $0$ y $3$, podemos encontrar un conjunto completo de puntos dentro del dominio de $g$ tal que $g (x, y) = c$:

Como $9 − c^2\gt 0$, esto describe un círculo de radio $\sqrt{9 − c^2}$ centrado en el origen. Cualquier punto en este círculo satisface la ecuación $g (x, y) = c$. Por lo tanto, el rango de esta función se puede escribir en notación de intervalo como $[0,3]$.