Solución

Apartado a.

Desarrolla el vector w en un vector con un componente yy en cero, y un vector con un componente x cero:

w=⟨3,−4⟩=3i−4j.\bold{w} = \lang 3, −4\rang = 3\bold{i} − 4\bold{j}.

Apartado b.

Como u es un vector unitario, el punto final se encuentra en el círculo unitario cuando el vector se coloca en la posición estándar (Figura 2.20).

u=⟨cos60o,sen60o⟩=⟨12,32⟩=12i+32j\begin{aligned} \bold{u} &= \lang cos60^o, sen60^o\rang\\ &=\bigg \lang \frac{1}{2}, \frac{\sqrt{3}}{2}\bigg\rang\\ &=\frac{1}{2}\bold{i} + \frac{\sqrt{3}}{2}\bold{j} \end{aligned}

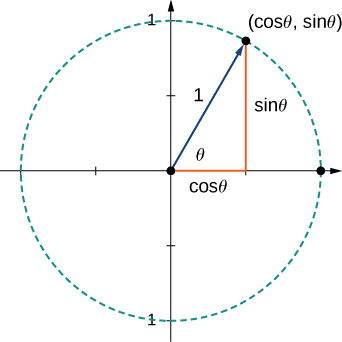
Figura 2.20. El punto terminal de u se encuentra en el círculo unitario (cosθ,senθ)(cos\theta, sen\theta).