Solución
La gráfica de r=3sen(2θ) es la siguiente.
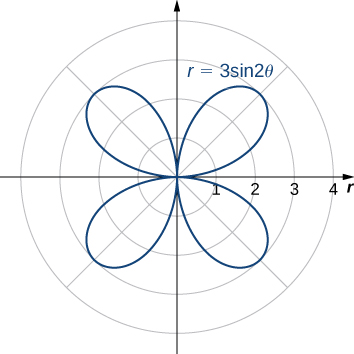
Figura 1.31 Gráfica de r=3sen(2θ).
A=21∫αβ(f(θ))2dθ=21∫0π/2(3sen(2θ))2dθ=21∫0π/29sen2(2θ)dθ
Para evaluar esta integral, usa la fórmula sen2α=(1−cos(2α))/2 con α=2θ:
A=21∫0π/29sen2(2θ)dθ=29∫0π/221−cos(4θ)dθ=49(∫0π/21−cos(4θ)dθ)dθ=49(θ−4sen(4θ))0π/2=49(2π−4sen(2π))−49(0−4sen4(0))=89π

