Solución

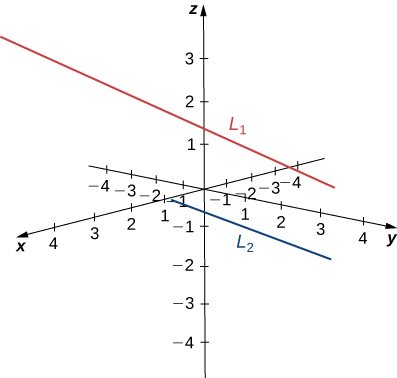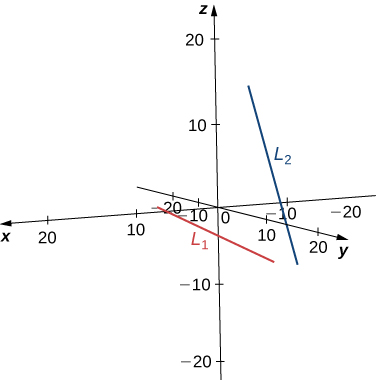
Apartado a

La recta L1L_1 tiene el vector de dirección v1=⟨2,1,1⟩\bold{v}_1 = \lang 2,1,1\rang; la recta L2L_2 tiene el vector de dirección v2=⟨1,3,−2⟩\bold{v}_2 = \lang1,3, −2\rang. Debido a que los vectores direccionales no son vectores paralelos, las rectas se intersecan o se sesgan (oblicuan).

Para determinar si las rectas se cortan, vemos si hay un punto, (x,y,z)(x, y, z), que se encuentra en ambas rectas. Para encontrar este punto, usamos las ecuaciones paramétricas para crear un sistema de igualdades:

2s−1=t−3;s−1=3t+8;s−4=5−2t2s−1=t−3;s−1=3t+8;s−4=5−2t

Por la primera ecuación, t=2s+2.t = 2s + 2. Sustituyendo en la segunda ecuación se obtiene

s−1=3(2s+2)+8s−1=6s+145s=−15s=−3\begin{aligned} s-1 &= 3(2s+2)+8\\ s-1 &= 6s +14\\ 5s &= -15\\ s &= -3 \end{aligned}

La sustitución en la tercera ecuación, sin embargo, produce una contradicción:

s−4=5−2(2s+2)s−4=5−4s−45s=5s=1\begin{aligned} s-4 &= 5−2(2s+2)\\ s-4 &= 5-4s-4\\ 5s &= 5\\ s &= 1 \end{aligned}

No existe un punto único que satisfaga las ecuaciones paramétricas para L1L_1 y L2L_2 simultáneamente. Estas rectas no se cortan, por lo que son asimétricas (consulte la siguiente figura).

Apartdo b

La recta L1L_1 tiene el vector de dirección v1=⟨1,−1,1⟩\bold{v}_1 = \lang 1, −1,1\rang y pasa a través del origen, (0,0,0)(0,0,0). La recta L2L_2 tiene un vector de dirección diferente, v2=⟨2,1,1⟩\bold{v}_2 = \lang 2,1,1\rang, por lo que estas rectas no son paralelas o iguales. Supongamos que rr representa el parámetro para la recta L1L_1 y que ss representa el parámetro para L2L_2:

x=ry=−rz=r\begin{aligned} x &= r\\y &= -r\\z &= r\end{aligned} x=2s+3y=sz=s+2\begin{aligned} x &= 2s+3\\y &= s\\z &= s+2\end{aligned}

Resuelve el sistema de ecuaciones para encontrar r=1r = 1 y s=−1s = −1. Si necesitamos encontrar el punto de intersección, podemos sustituir estos parámetros en las ecuaciones originales para obtener (1,−1,1)(1, −1,1) (ver la siguiente figura).

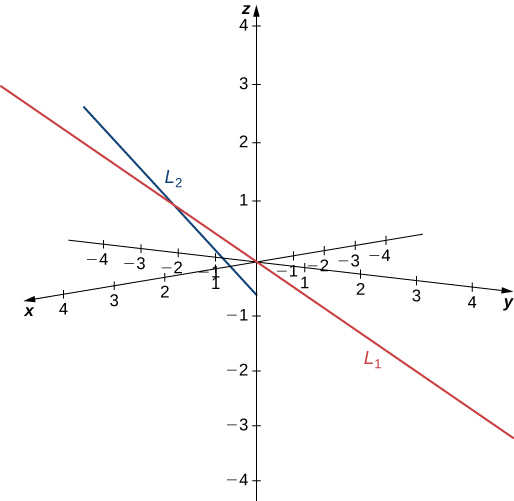
Apartado c

Las rectas L1L_1 y L2L_2 tienen vectores direccionales equivalentes: v1=⟨6,−2,3⟩\bold{v}_1 = \lang 6, −2,3\rang. Estas dos rectas son paralelas (ver la siguiente figura).