Solución

A medida que el punto $P$ viaja alrededor de la espiral en sentido antihorario, su distancia $d$ desde el origen aumenta. Supón que la distancia $d$ es un múltiplo constante $k$ del ángulo $θ$ que el segmento de línea $OP$ forma con el eje x positivo. Por lo tanto $d(P,O) = kθ$ , donde $O$ es el origen. Ahora usa la fórmula de distancia y algo de trigonometría:

\begin{aligned} d(P,O) &= kθ\\ \sqrt{(x-0)^2+(y-0)^2} &= karctan\left(\frac{y}{x}\right)\\ \sqrt{x^2+y^2} &= karctan\left(\frac{y}{x}\right)\\ arctan\left(\frac{y}{x}\right) &= \frac{\sqrt{x^2+y^2}}{k}\\ y &= xtan\left(\frac{\sqrt{x^2+y^2}}{k}\right) \end{aligned}

Aunque esta ecuación describe la espiral, no es posible resolverla directamente para $x$ o $y$ . Sin embargo, si usamos coordenadas polares, la ecuación se vuelve mucho más simple. En particular, $d(P, O) = r$ , y $θ$ es la segunda coordenada. Por lo tanto, la ecuación para la espiral se convierte en $r = kθ$ . Observa que cuando $θ = 0$ también tenemos $r = 0$ , por lo que la espiral emana del origen. Podemos eliminar esta restricción agregando una constante a la ecuación. Entonces la ecuación para la espiral se convierte en $r = a + kθ$ para las constantes arbitrarias $a$ y $k$ . Esto se conoce como una espiral de Arquímedes, debida al matemático griego Arquímedes.

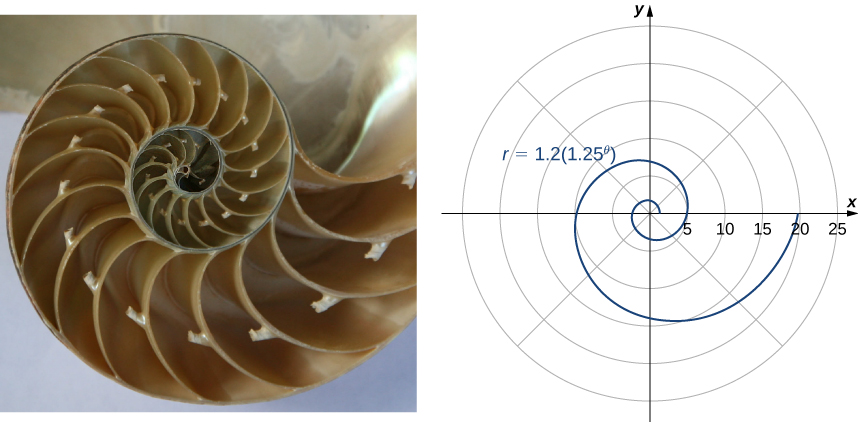
Otro tipo de espiral es la espiral logarítmica, descrita por la función $r = a • b^θ$ . En la siguiente figura se muestra una gráfica de la función $r = 1.2(1.25^θ)$ . Esta espiral describe la forma de la concha del nautilo con cámara.

Figura 1.26 Una espiral logarítmica es similar a la forma de la concha de nautilus (crédito: modificación del trabajo de Jitze Couperus, Flickr).