Solución

a.  Geométrica

  1. Dibuja el vector en el plano de coordenadas (Figura 2.12).
  2. El punto final está 44 unidades a la derecha y 22 unidades hacia abajo desde el punto inicial.
  3. Encuentra el punto que está 44 unidades a la derecha y 22 unidades hacia abajo desde el origen.
  4. En posición estándar, este vector tiene un punto inicial (0,0)(0,0) y un punto final (4,−2)(4, −2):v=⟨4,−2⟩\bold{v} = \lang 4, -2 \rang

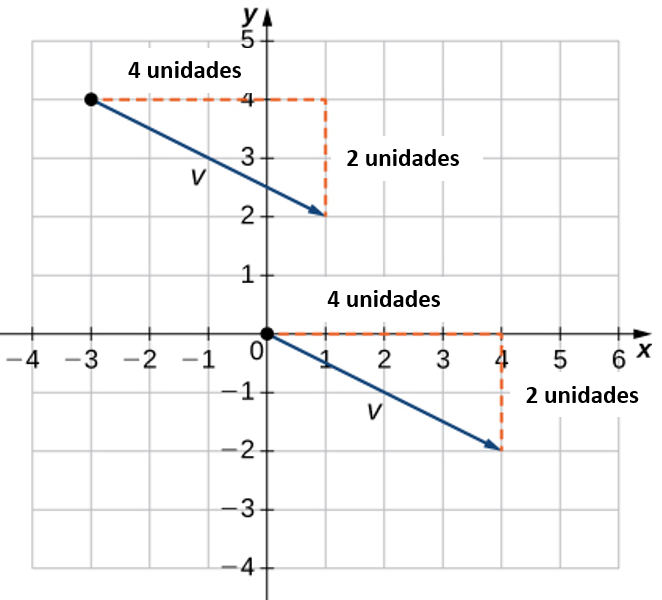
Figura 2.10. Estos vectores son equivalentes.

b. Algebraica

En la primera solución, usamos un boceto del vector para ver que el punto final se encuentra 4 unidades a la derecha. Podemos lograr esto algebraicamente encontrando la diferencia de las coordenadas xx

xt−xi=1−(−3)=4x_t − x_i = 1 - (- 3) = 4

Del mismo modo, la diferencia de las coordenadas yy muestra la longitud vertical del vector.

yt−yi=2−4=−2y_t − y_i = 2 − 4 = −2

Entonces, en forma de componente,

v=⟨xt−xi,yt−yi⟩=⟨1−(−3),2−4⟩=⟨4,−2⟩\begin{aligned} \bold{v} &= \lang x_t - x_i, y_t - y_i \rang \\ &= \lang 1 - (- 3), 2 − 4 \rang \\ &= \lang 4, -2 \rang \end{aligned}