Planifica el nuevo curso escolar 2024- 2025 en Bachillerato con los recursos del Proyecto Descartes
Escrito por Ángel Cabezudo BuenoEste artículo forma parte de una serie planificada por Red Educativa Digital Descartes al comienzo de un nuevo curso escolar en España y dirigido principalmente a los profesores de Bachillerato. Sin duda también será de utilidad si el proceso de enseñanza y aprendizaje va a ir dirigido a alumnos de un nivel educativo asimilado para edades comprendidas entre los 15 y 18 años de otros países.
Red Educativa Digital Descartes (RED Descartes), asociación no gubernamental sin ánimo de lucro constituida el 1 de junio de 2013 que tiene como fin promover la renovación y cambio metodológico en los procesos de aprendizaje y enseñanza de las Matemáticas, y también en otras áreas de conocimiento, utilizando los recursos digitales interactivos generados en el Proyecto Descartes. En particular, para la consecución de este fin, se promueve el desarrollo y difusión de la herramienta de autor denominada "Descartes".
Descartes y el Proyecto Descartes inició su andadura en junio del año 1998 en un contexto matemático, pero ha ido evolucionando y ampliando su ámbito de aplicación a otras áreas científicas, sociales y literarias.
El repositorio que acumula hoy en día es impresionante y se organiza en subproyectos donde se incluyen todos los materiales interactivos en HTML5 adaptados y desarrollados con DescartesJS que pueden utilizarse en cualquier ordenador o dispositivo móvil independientemente del sistema operativo que porten. Nuestra tarea como asociación se centra en esta sección y aquí podría el docente dirigirse para revisar su contenido y seleccionar para cada momento de su programación los materiales más adecuados para su uso en el aula, bien directamente o previa adaptación, o en su caso la adecuada recomendación de uso a sus alumnos. Estos materiales pueden ser utilizados en línea o en local pues todos ellos pueden ser descargados e instalados en el equipo informático de que se disponga y ¡totalmente gratis!
Cada subproyecto fue diseñado con un determinado propósito, tiene su cabida en un determinado área del conocimiento y adecuado a un determinado nivel educativo.
A continuación hacemos una reseña de aquellos subproyectos que contiene materiales didácticos para el nivel de Bachillerato, o en otro caso revisado y filtrado convenientemente por el profesor, indicando las novedades de los recursos que se han incorporado a nuestro repositorio desde la publicación del artículo similar, al comienzo del curso escolar y académico 2023-2024, anterior hasta este momento.
| Subproyecto: Unidades Didácticas | |||
|
Las unidades didácticas son bloques de programación docente, base del desarrollo del proceso de enseñanza y aprendizaje y que integran una metodología y una planificación temporal para la consecución de los objetivos contemplados. Las unidades didácticas son un nivel docente de concreción del currículo que refleja el qué, cómo y cuándo enseñar y evaluar. |
La estructura de una unidad didáctica incluye una introducción, los objetivos y un índice de contenidos. Los siguientes enlaces conducen al índice por niveles Matemáticas Primer Curso Segundo Curso Física y Química Primer Curso Segundo Curso |
||
| Subproyecto: Miscelánea | |||
|
Recoge escenas aisladas que tratan aspectos muy variados del currículo de Matemáticas y que pueden servir para que el profesorado las utilice directamente para ilustrar conceptos y técnicas básicas, o para que construyan con ellas actividades y propuestas de trabajo en el aula. |
El profesorado podrá disponer de escenas para crear sus propias lecciones, creando actividades para que el alumnado investigue, deduzca y llegue a conclusiones por sí mismo.
Matemáticas
Primer Curso https://proyectodescartes.org/miscelanea/nivel_bach_primero.htm Segundo Curso https://proyectodescartes.org/miscelanea/nivel_bach_segundo.htm Novedad: SUDOKU DescartesJS Novedad: Camuflar monedas |
||
| Subproyecto: iCartesiLibri (Libros intractivos) | |||
|
Nuestro diseño hace que estos libros sean accesibles y plenamente operativos en cualquier ordenador personal o en cualquier dispositivo móvil tipo tableta y smartphone, independientemente del sistema operativo que porte. El interes de estos libros digitales radica en que incorporan recursos multimedia con los que el usuario puede interactuar cuando le interese complementar la lectura del texto con un vídeo, una grabación en audio o un material interactivo, básicamnete escenas realizadas con DescartesJS. Los hipervínculos también le pueden conducir a la consulta de recursos como defininiciones, imágenes y artículos publicados en la web y que se relaciona con algun contenido del libro lo que supone un refuerzo y apoyo para una mejor comprensión. |
La temática del subproyecto iCartesiLibris es muy variada y está en constante ampliación dado que cualquier profesor puede redactar y publicar su propio libro digital interactivo disponiendo para ello del libro titulado “Diseño de libros intractivos” ISBN 978-84-18834-27-1 que puede ser descargado en formato ZIP y consultado accediendo al apartado de Formación del Índice Materiales del subproyecto.
Los temas que el profesor interesado puede consultar en iCartesiLibri son, como hemos dicho anteriormente, muy variados y con ello está abierto a otros nuevos.
|
||
| Proyecto Prometeo - Bachillerato UNAM | |||
|
El proyecto Prometeo está promovido por el Departamento de Educación del Instituto de Matemáticas de la UNAM (Universidad Nacional Autónoma de México) e incluye las unidades didácticas interactivas creadas por el Equipo Descartes. Las unidades consisten en una o varias escenas interactivas diseñadas para abordar temas principalmente de matemáticas y física, aunque también hay de otras materias. Los contenidos se desarrollan y cubren diferentes niveles educativos. Los diferentes materiales del proyecto Prometeo se organizan según el nivel educativo al que va dirigido y también su temática. En la web de RED Descartes hemos incluido los siguientes. Dado que no existe una equivalencia unívoca entre los niveles de los sistemas educativos Mexicano y Español el profesor en busca de recursos según convenencia debería consultar |
La secuencia didáctica utilizada se encuentra conformada por: 1. Introducción; 2. Desarrollo; 3. Ejercicios; y 4. Evaluación. En la evaluación se presentan 5 preguntas de opción múltiple. |
||
| Proyecto Newton - Problemas | |||
|
Esta página recoge enunciados de problemas que tratan aspectos muy diversos de Física y Química y que pueden servir para que el profesorado los utilice directamente para ilustrar los conceptos o para construir con ellos actividades y propuestas de trabajo en el aula. El profesorado podrá disponer de materiales para que el alumnado investigue, deduzca y llegue a conclusiones por sí mismo. . |
Es más, el profesorado podrá adaptar estos problemas a sus necesidades (si así lo desea) usando la herramienta de autor Descartes. Esta web recoge escenas aisladas que tratan aspectos muy variados del currículo de Física y Química en forma de resolución de un problema. Esta página pretende ser una zona de la Red Descartes donde el alumno pueda desmenuzar con la ayuda de las TIC los problemas que con mayor carga conceptual se incorporan en el currículo de Física y Química Los recursos de este subproyectos se centan en los niveles de 4º curso Secundaria Obligatoria y 1º y 2º cursos de Bachillerato, del plan educativo español. La estructura didáctica sigue el esquema siguiente
|
||
| Proyecto Un_100 | |||
|
El proyecto Un_100 recoge 101 unidades didácticas o recursos educativos de las áreas de Matemáticas y Física y son para el nivel de Licenciatura, algunos también pueden ser usados en el bachillerato. En su elaboración han participado académicos de México, España, Colombia y Chile. Casi todos pueden ser visualizados en tabletas y smartphones, además de en ordenadores con cualquier sistema operativo, y para ello basta contar con un navegador de internet actualizado a los estándares de HTML5.
|
Todas las unidades tienen un mismo esquema o plantilla común, con un diseño gráfico genérico, y sobre él cada desarrollador ha incorporado los contenidos y ha elaborado su secuencia didáctica personal. Se distinguen cuatro fases o momentos: Motivación, Inicio, Desarrollo y Cierre, y se complementa con un acceso a la documentación de la unidad en la que además se incluyen los créditos. El siguiente índice es una clasificación por áreas de contenidos y aunque algunos estén indicados para un nivel de Licenciatura podrían ser incluidos en parte o en su totalidad en un nivel de Bachillerato según el plan educativo español.
|
||
| Proyecto Ingeniería y Tecnología | |||
|
El proyecto Ingeniería y Tecnología tiene como objetivo ofrecer contenidos digitales que se encuadran en diferentes áreas de conocimiento y que en la mayoría de los currículos de programas de ingeniería o formación tecnológica se agrupan en cuatro apartados principales: ciencias básicas, ciencias de ingeniería, ciencias sociales y humanas, y aspectos o contenidos específicos de la profesión. |
El apartado de Ciencias básicas incluye una relación de materias que pueden ser de utilidad como complemento al planificar estrategias educativas en el desarrollo del temario de Bachillerato del plan de estudios español en las siguientes áreas: Podrá observarse cierta variedad organizativa, funcional o estética dependiendo del subproyecto de RED Descartes del que procede el objeto educativo enlazado, pero comparten una misma finalidad didáctica y una común estrategia educativa.
|
||
| Proyecto Plantillas con DescartesJS | |||
|
Con este proyecto es posible generar atractivos juegos, puzles, actividades y test de memoria, de arrastre y asociación, sin más que realizar simples y usuales tareas de edición de imágenes y de ficheros de texto “plano” (es decir sin incluir formato codificado). Para ello se usan escenas, previamente desarrolladas, como cajas negras que recibiendo como entrada un conjunto de datos preparados por el profesor o profesora aportan una actividad interactiva que pueden utilizarse e incorporarse en el proceso de enseñanza-aprendizaje. |
Los materiales que pueden elaborarse tienen encuadre en cualquier nivel educativo y materia, ya que es el contenido en sí el que marca su ubicación. Por ejemplo, un test de asociación puede establecerse entre poliedros regulares y sus denominaciones o bien entre imágenes de animales y sus nombres en castellano o en otro idioma; o en un test de memoria es posible identificar figuras geométricas con igual o análoga forma o bien animales de la misma especie, o palabras sinónimas. En definitiva la creatividad docente es la que mueve la herramienta en la consecución de los logros educativos. Las actividades que el docente tiene que realizar utilizando plantillas para el desarrollo de estos materiales se encuadran en tres tipos de acciones:
Sencillas tareas que permitirán la construcción rápida y fácil de recursos didácticos sin necesidad de estudiar ni conocer la herramienta de edición de Descartes. Todo irá acompañado de su correspondiente guía o tutorial para, a partir de la plantilla, abordar y lograr el recurso deseado. En el índice del subproyecto Plantillas se encuentra el apartado de Tutoriales donde el docente interesado encontrará un Manual completo de plantillas El apartado de Aplicaciones incluye una serie de unidades organizadas en áreas de conocimiento y niveles educativos desarrolladas por el profesorado y en algunos casos por algunos de sus alumos a partir de las plantillas existentes. Para el nivel bachillerato y el área de matemáticas tenemos los siguientes rescursos Matemáticas |
||
| Revista Digital | |
|
Desde RED Descartes ofrecemos nuestra Revista Digital, Panhispánica – Educativa - Interactiva, una plataforma cuyo primer número apareció en 2021 con periodicidad semestral y que tiene como principal objetivo difundir cualquier contenido relacionado con el Proyecto Descartes. |
Esperamos que la Revista Digital interese al profesor de Bachillerato y que pudiera compartir con sus alumnos, en algun caso, si lo considera adecuado . El formato que toma la revista es la de libro digital interactivo. Los artículos tienen una temática muy diversa, aunque siempre relacionada con los objetivos del Proyecto Descartes y su herramienta homónima Descartes, sin excluir a ningún otro recurso, como soporte en el proceso de enseñanza-aprendizaje en cualquiera de sus ámbitos científico, tecnológico, pedagógico, social, lingüístico-literario… |
No podemos terminar este artículo sin mencionar dos herramientas más para el usuario interesado en utilizar los recursos que hemos presentado anteriormente.
Las opciones de búsqueda de recursos
El primero consiste mostrar los buscadores que la Web de Red Educativa Digital Descartes pone a su disposición para localizar y consular los recursos. Para ello puede visionar el siguiente vídeo que explica como hacerlo.
Como aprender a programar las escenas interactivas de DescartesJS
Como dijo Ildefonso Fernández Trujillo (D.E.P.) en el correspondiente articulo de 2022.
... es de señalar la posibilidad de adaptar fácilmente los contenidos de dichos recursos a las necesidades propias o a las características del aula, especialmente las Misceláneas que con un mínimo de cambios pueden convertirse en herramientas propias que satisfagan las necesidades didácticas inmediatas. Todo lo que necesitamos para realizar los cambios en los recursos es el 'Editor Descartes' herramienta (editor) intuitiva y de uso fácil.
Una vez que se ha visto la estructura de un recurso y se ha hecho uso de él se intuye la facilidad para la creación de uno parecido para lo cual disponemos de varios libros interactivos en el subproyecto iCartesiLibri, 'Formación en DescartesJS', que detallan todas las funcionalidades y procedimientos del editor Descartes y también está disponible una documentación exhaustiva en línea.
Esperamos y deseamos que este artículo le haya sido de ayuda y pueda encontrar en Red Educativa Digital Descartes todo que necesite.
Planifica el curso escolar 2024-2025 con los recursos del Proyecto AJDA
Escrito por Jesús Manuel Muñoz CalleEl curso escolar 2024-2025 trae consigo una serie de innovaciones y mejoras en el Proyecto AJDA, de la Red Descartes diseñadas para enriquecer la experiencia educativa y facilitar la integración de herramientas digitales avanzadas en el aula. A continuación, presentamos las principales novedades y recursos que están disponibles para docentes y estudiantes.
Nuevas publicaciones
- Libro interactivo "Juegos didácticos. Proyecto AJDA": Este libro ofrece una guía completa sobre cómo utilizar los juegos AJDA para potenciar el aprendizaje en el aula.
- Libro interactivo "Gamificando con juegos AJDA": Un recurso que explora cómo la gamificación puede transformar la experiencia educativa, proporcionando estrategias prácticas y ejemplos concretos.
- Libro interactivo "Diseño de contenidos digitales con inteligencia artificial". Se trata de la generación de recursos digitales, incluidos juegos didácticos, mediante el empleo de inteligencia artificial.
- Artículos en la revista digital de la Red Descartes.
- Publicaciones periódicas en el blog de Descartes.
Actualización y mejora de los juegos AJDA
Este año, todos los juegos del Proyecto AJDA han sido sometidos a una profunda revisión y mejora. Con un total de 520 juegos didácticos, se han realizado, entre otras, las siguientes actualizaciones:
- Nuevas funcionalidades: Se han incorporado mejoras en la gestión de preguntas, nuevos parámetros de configuración, y la capacidad de guardar y continuar partidas, lo que permite una mayor flexibilidad en su uso pedagógico.
- Unificación de estilo: Se han homogeneizado los elementos visuales de todos los juegos, como botones, títulos, fondos, colores e imágenes, asegurando una experiencia coherente y atractiva.
- Adaptación a DescartesJS: Los juegos se han actualizado a la última versión de DescartesJS, garantizando su compatibilidad y funcionamiento óptimo en las plataformas más recientes.
- Contenido adicional: Se han añadido nuevos ficheros de contenido que amplían las opciones educativas disponibles para los docentes.
Estas mejoras están diseñadas para hacer de los juegos AJDA una herramienta aún más potente y versátil, adaptada a las necesidades actuales del aula.
Mantenimiento y adecuación de las webs AJDA
- Ampliación y actualización del curso de formación “Aplicación de juegos didácticos en el aula”.
- Ampliación y actualización del curso de formación Creación de animaciones y juegos interactivos para el aula”.
- Inclusión de nuevos vídeos.
- Inclusión oficial de los logos del Proyecto AJDA.
- Actualización y mejora del generador de ficheros.
Avances en el Proyecto Gamifica
El Proyecto Gamifica, una colaboración en curso entre el Proyecto AJDA y el departamento de Ingeniería Telemática de la ETSI de la Universidad de Sevilla, ha continuado su crecimiento durante el curso 2024-2025. Entre los principales logros se encuentran:
- Presentación de dos nuevos Trabajos de Fin de Grado (TFG), con cinco más en desarrollo, todos centrados en el uso de juegos AJDA.
- En desarrollo de cinco TFG específicamente diseñados para ser utilizados en el Proyecto Gamifica.
- Avances en la web de Gamifica, que está casi completamente operativa, y la presentación oficial del logo del proyecto.
- Preparación de 5 juegos AJDA para utilización en el Proyecto Gamifica.
- Mantenimiento y actualización del servidor en la nube del Proyecto Gamifica, que ahora incluye nuevas funcionalidades telemáticas para mejorar la experiencia de los usuarios.
- Elaboración de la documentación relacionada con los trabajos de investigación desarrollados y en desarrollo: memorias, instrucciones, guías, presentaciones, vídeos, resúmenes, esquemas, cuadrantes, recursos, etc.
- Puesta en práctica en el aula de nuevas metodologías didácticas basadas en los juegos didácticos con motivo de la realización de un TFG.
Estos esfuerzos refuerzan el papel del Proyecto AJDA en la investigación y desarrollo de nuevas metodologías educativas basadas en el uso de juegos didácticos.
Recursos de enseñanza-aprendizaje del Proyecto Descartes para Educación Secundaria
Escrito por Montserrat Gelis BoschLa Red Educativa Digital Descartes es una plataforma que ofrece una amplia variedad de recursos didácticos orientados a mejorar la enseñanza de diversas asignaturas, principalmente en áreas como matemáticas, ciencias y tecnología.
Los recursos de Descartes están elaborados en formato digital e interactivo, permitiendo a los docentes integrarlos fácilmente en sus clases, ya sea de manera presencial o virtual. Además, los contenidos se ajustan a los currículos educativos, lo que asegura su pertinencia y utilidad en el proceso de enseñanza-aprendizaje.
Este artículo ofrece una visión general de los materiales educativos digitales de la RED Descartes para Secundaria, destacando sus beneficios y presentando los nuevos recursos producidos este año, que serán de gran utilidad en el contexto educativo actual.
 Proyecto Canals Proyecto Canals |
La mayoría de los objetos interactivos creados con los materiales de M.A. Canals están dirigidos a estudiantes de primaria, aunque también se pueden encontrar algunas actividades interesantes para alumnos de 1º de la ESO
 Proyecto "ED@D" (Educación Digital con Descartes) Proyecto "ED@D" (Educación Digital con Descartes) |
Recursos educativos digitales interactivos para la Educación Secundaria Obligatoria (ESO) en las áreas de Matemáticas, Ciencias Naturales y Física y Química, diseñados para ser utilizados tanto en la enseñanza presencial como en la formación a distancia.
Matemáticas (Castellano/ Català/ Galego/ Português)
Ciencias Naturales
Física y Química
 Proyecto Unidades didácticas Proyecto Unidades didácticas |
Numerosas unidades didácticas de Matemáticas y de Física y Química han sido desarrolladas por docentes, quienes han plasmado en ellas su experiencia adquirida en el aula. Este valioso conocimiento se ha enriquecido con el uso de escenas interactivas de Descartes, que facilitan la visualización de conceptos, la práctica de procedimientos y el redescubrimiento de las matemáticas y las ciencias.
Matemáticas. Índice por nivel y curso. Secundaria Obligatoria (ESO)
Matemáticas. Índice temático
Física y Química. Índice por nivel y curso. Secundaria Obligatoria (ESO)
Física y Química. Índice temático
 Proyecto Plantillas con Descartes-JS Proyecto Plantillas con Descartes-JS |
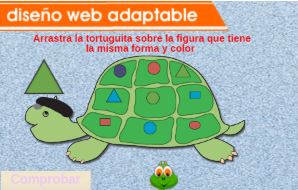
El objetivo de este proyecto es demostrar cómo es posible crear atractivos juegos, puzles, actividades y test de memoria, de arrastre y asociación mediante tareas simples y comunes de edición de imágenes y archivos de texto. Para ello, se utilizan escenas previamente desarrolladas que, al recibir un conjunto de datos preparados por el docente, generan una actividad interactiva que puede integrarse en el proceso de enseñanza-aprendizaje.
El apartado de aplicaciones incluye una serie de unidades desarrolladas por el profesorado a partir de las plantillas propuestas.
Materiales:
Aplicaciones:
Matemáticas:
Ciencias Naturales:
Ciencias Sociales:
Lengua:
Arte:
 Proyecto Competencias Proyecto Competencias |
Objetos de aprendizaje interactivos diseñados para la formación y evaluación competencial. Estos contenidos se basan en las unidades liberadas de PISA, así como en las Pruebas de Evaluación de Diagnóstico de diversas comunidades autónomas españolas. Con la plataforma Descartes, estas unidades se transforman, adquiriendo dinamismo e interactividad, lo que permite a los usuarios adquirir competencias clave. De este modo, el recurso evoluciona de ser meramente informativo a convertirse en una herramienta formativa efectiva.
 Proyecto ASIPISA Proyecto ASIPISA |
ASIPISA es el nombre de un proyecto dedicado al desarrollo de materiales educativos digitales e interactivos, basados en las unidades liberadas del Programa Internacional PISA. Este proyecto introduce variabilidad mediante semillas aleatorias, lo que dinamiza el contenido, evita la repetición y aumenta su potencial instructivo.
Escenas aisladas que abordan diversos aspectos del currículo de Matemáticas, útiles para que el profesorado las emplee directamente para ilustrar conceptos y técnicas básicas, o para desarrollar actividades y propuestas de trabajo en el aula. Este recurso pretende funcionar como una caja de herramientas matemáticas, proporcionando apoyo y refuerzo al trabajo diario del docente. Los profesores podrán utilizar estas escenas para diseñar sus propias lecciones y actividades, fomentando la investigación, la deducción y la autonomía en el aprendizaje del alumnado.
Índice temático:
Índice por nivel y curso. Secundaria Obligatoria (ESO)
El objetivo de este proyecto es conceptualizar y desarrollar libros dinámicos, interactivos y multimedia, enfocados en el aprendizaje y diseñados para potenciar la educación de personas que aprenden a aprender, adquieren autonomía y desarrollan competencias para afrontar su trayectoria vital.
Su diseño garantiza que estos libros sean accesibles y plenamente operativos en cualquier ordenador personal o dispositivo móvil, ya sea tableta o smartphone, independientemente del sistema operativo.
 Proyecto Newton Proyecto Newton |
Enunciados de problemas que tratan aspectos muy diversos de Física y Química y que pueden servir para que el profesorado los utilice directamente para ilustrar los conceptos o para construir con ellos actividades y propuestas de trabajo en el aula.
Telesecundaria es una modalidad del sistema educativo en México. En este subproyecto de RED Descartes, se recopilan y difunden los objetos de Telesecundaria desarrollados con esta herramienta.
 Proyecto Aplicación de Juegos Didácticos en el Aula (AJDA) Proyecto Aplicación de Juegos Didácticos en el Aula (AJDA) |
Los juegos didácticos son herramientas poderosas en el ámbito educativo, ya que combinan el entretenimiento con el aprendizaje. A través de los juegos, los estudiantes pueden desarrollar habilidades cognitivas como la resolución de problemas, el pensamiento crítico y la toma de decisiones, de una manera lúdica y atractiva. Además, los juegos fomentan la competencia sana y el trabajo en equipo, lo que mejora las habilidades sociales de los estudiantes. El aprendizaje a través del juego también reduce la ansiedad y el estrés asociados con la evaluación tradicional, creando un ambiente más positivo y propicio para el aprendizaje.
La Aplicación de Juegos Didácticos en el Aula (AJDA) es un proyecto educativo que ofrece una amplia variedad de juegos didácticos, diseñados para ser utilizados a través de metodologías de gamificación. El proyecto incluye más de 500 juegos que pueden aplicarse con alumnos de todas las etapas, materias y niveles educativos.
Entre las novedades de este año, se presentan dos libros informativos para la creación de juegos:
 Proyecto Estudio Europeo de Competencia Lingüística (EECL) Proyecto Estudio Europeo de Competencia Lingüística (EECL) |
En esta web se presentan las preguntas del primer Estudio Europeo de Competencia Lingüística, realizado en 2011, adaptadas como recursos interactivos TIC.
| Nivel | Comprensión Lectora | Comprensión oral | ||||
|
A1 A2 B1 B2 |
|
|
 Proyecto GEOgráfica Proyecto GEOgráfica |
Colección de recursos educativos interactivos destinados a facilitar el aprendizaje de la Geografía mundial, abarcando diversos niveles de detalle, desde el contexto global hasta el local. Estos recursos cubren diferentes ámbitos disciplinarios, incluyendo la Geografía general, física, humana y regional.
Nuevos materiales publicados:
En un mundo educativo en constante evolución, la RED Descartes añade cada año nuevos recursos didácticos fundamentales para mantener la enseñanza actualizada y relevante. A continuación, se presenta una lista de las nuevas unidades creadas en diversos proyectos de la RED Descartes durante el curso 2023-24:
Novedades Proyecto Miscelánea:
Novedades Proyecto iCartesiLibri:
Novedades Proyecto Plantillas:
En el siguiente vídeo se presenta una pequeña muestra de las diversas actividades incluidas en los distintos proyectos de la RED para Secundaria:
La vuelta al cole con Descartes en 2024
Escrito por José Antonio Salgueiro GonzálezLos profesionales de la enseñanza siempre empezamos los cursos escolares con ilusión, entusiasmo y emoción, atributos que esperamos transmitir, como en años anteriores, a todos los agentes que intervienen en la educación. Por todo ello, ofrecemos el acceso gratuito a nuestros recursos para el personal docente, el alumnado y sus familias, unos recursos interactivos que han demostrado su gran utilidad tanto en la enseñanza presencial como en la enseñanza a distancia.
Como gran novedad, presentamos Plantillas de fracciones circulares para Educación Primaria, un libro interactivo para la formación del profesorado que pretende abarcar el currículo de matemáticas desde los cinco a los doce años, presentando modelos de actuación y estrategias didácticas con plantillas que contienen círculos fraccionados o sectores circulares. Además, incorpora los recursos y orientaciones necesarias para su aplicación directa con el alumnado.
Más...
Boletín 1 - Novedades IA Generativas
Escrito por Juan Guillermo Rivera Berrío¡Nos complace anunciar el lanzamiento de nuestro boletín mensual, "Novedades IA Generativas"!
En un mundo donde la tecnología avanza a pasos agigantados, mantenerse al día con las últimas herramientas y mejoras en el campo de la inteligencia artificial es esencial. Este boletín está diseñado para ofrecerte un resumen claro y conciso de las innovaciones más recientes en IA generativa, desde nuevas aplicaciones y algoritmos hasta actualizaciones en herramientas existentes.
Cada mes, te brindaremos información valiosa y práctica, destacando cómo estas tecnologías pueden impactar tu trabajo, mejorar tu productividad, y abrir nuevas posibilidades creativas. No te pierdas la oportunidad de estar a la vanguardia de la revolución tecnológica. ¡Ingresa hoy a "Novedades IA Generativas" y mantente informado sobre lo último en IA generativa
|
En el siguiente video, puedes conocer más sobre nuestro boletín: |
 |
Asamblea general en la ETSIIT de Santander
Escrito por José Antonio Salgueiro GonzálezUn año más, y como es tradición desde siempre, marcada por el calendario escolar, hemos celebrado nuestra Asamblea General Ordinaria en forma presencial, simultaneada con modalidad virtual para aquellos socios y socias que no han podido asistir físicamente. El acto tuvo lugar en esta ocasión en la Escuela Técnica Superior de Ingenieros Industriales y de Telecomunicación de Santander, capital de la comunidad autónoma de Cantabria, ubicada en la costa norte de España, lugar al que nos desplazamos desde distintos puntos geográficos de la península: Burgos, Santomera, Lebrija, Valladolid, Baza, Madrid, Córdoba, Santiago de Compostela, Logroño, Cádiz, Zaragoza y Barcelona. Para quien suscribe este artículo fue un honor presentar personalmente a nuestro amigo Manuel Muñoz, quien asistía por primera vez.
Durante una fructífera jornada hemos tratado, grosso modo, asuntos de relevancia como las mejoras técnicas experimentadas en el núcleo del libro interactivo, incorporando nuevas utilidades o mejorando las existentes, recordando que, como software libre, se encuentra alojado en el repositorio de código GitHub, desde donde puede descargarse, gracias al soporte proporcionado por el Instituto de Matemáticas de la Universidad Nacional Autónoma de México. En el ámbito de la formación, y dentro del programa de Educación Abierta de RED Descartes, desde Colombia se desarrolló, entre octubre de 2023 y febrero de 2024, la V Edición del curso para el Diseño de Libros Interactivos, cuyas sesiones se graban en vídeo y se difunden para el conocimiento libre. Además, con una periodicidad quincenal tienen lugar las reuniones en línea para compartir los avances en las investigaciones sobre aprovechamiento óptimo de la Inteligencia Artificial en la generación de contenido digital. De hecho, acabamos de publicar la obra "Diseño de contenidos digitales con inteligencia artificial". Si deseas participar en estas reuniones, puedes contactar con nosotros enviando un correo a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Hemos reflexionado sobre la revista digital de la RED Descartes, panhispánica, educativa e interactiva, cuyo séptimo número se publicó días antes de esta asamblea, de nuestra publicación electrónica seriada anual y el importante número de descargas que se producen (con objeto de usar en local todos nuestros recursos educativos abiertos), de haber alcanzado el centenar de libros interactivos publicados en nuestra biblioteca cartesiana y en nuestra librería, de la ampliación de contenidos en el Proyecto PI con nuevos recursos fruto de los cursos de formación en generación de recursos interactivos con Descartes JS, impartidos desde Colombia, de la ampliación igualmente del Proyecto Miscelánea y las líneas de trabajo en el subproyecto “Aplicación de juegos didácticos en el aula”, que alcanza ya los 520 juegos actualizados.
En otro orden de cosas, y como resulta preceptivo en estas asambleas, hemos tratado asuntos de gestión y organización, memoria y propuesta de actividades, cierre económico y propuesta de presupuestos.
Queremos mostrar desde aquí nuestro más sincero agradecimiento a la dirección de la Escuela Técnica Superior de Ingenieros Industriales y de Telecomunicación por el exquisito trato dispensado, así como por facilitar el desarrollo de la asamblea general de RED Descartes en la capital de la comunidad cántabra y, como no puede ser de otra manera por nuestra profesión, en un entorno educativo y académico.
Aprovechando la estancia en Santander, ciudad de reyes y pescadores, también conocida por la novia del mar, como le cantaba Jorge Sepúlveda, y con dos grandes anfitrionas, como son nuestras compañeras Solín y Elena, o Elena y Solín, comenzamos la primera jornada almorzando en el restaurante Golf Mataleñas, en una terraza con unas envidiables vistas a una de las más hermosas bahías del mundo y una suave temperatura, muy agradable para los que veníamos del sur. Después de la sobremesa iniciamos un paseo por el paraje natural colindante, con acantilados, verdes montañas y playas de blanca arena, como las de Mataleñas y el Sardinero, para concluir en el Parque de Mesones, junto a la estatua del escritor canario Benito Pérez Galdós, que llegó a la capital cántabra atraído por el novelista José María de Pereda y en ella escribió sus Episodios Nacionales.Tras un pequeño descanso, después del largo viaje, terminamos la jornada con una cena en el restaurante Bodega del Riojano.
Durante uno de los trayectos por la bella ciudad de Santander, nos encontramos con un enlosado en cierta calle que nos hizo deternos para examinar "Con mirada matemáTICa", algo muy peculiar en nuestra profesión:

Pues bien, nuestro amigo Luis Barrios se encuentra diseñando un recurso interactivo, evidentemente con la herramienta de autor DescartesJS, para investigar sobre esta composición geométrica.
La sesión matinal de la segunda jornada estuvo dedicada a nuestra asamblea general, como ya hemos descrito anteriormente, motivo, además, de nuestro traslado a Santander. Posteriormente, nos desplazamos a la Península de la Magdalena para disfrutar de aquel entorno privilegiado y ver el palacio homónimo, actualmente sede de la Universidad Internacional Menéndez Pelayo. Un largo paseo que nos abrió el apetito y pudimos disfrutar y gozar el paladar con la gastronomía cántabra en el Restaurante Gran Hotel Sardinero. Iniciamos la sesión vespertina, ilustrada y amena, gracias a Pilar Ruiz de la Cuesta, nuestra especialista en historia de Santander, comenzando en la Plaza de las Atarazanas, la catedral de Nuestra Señora de la Asunción, un paseo por los Jardines de Pereda hasta llegar al Centro Botín y las esculturas que homenajean a las víctimas del gran incendio que asoló la ciudad en 1941 y que destruyó su casco histórico. Continuamos hacia la Plaza Porticada o de Velarde, subimos para ver una preciosa vivienda de estilo neomudéjar y nos encaminamos hacia el paseo marítimo, deteniéndonos en el monumento a los Raqueros y en la escultura dedicada al poeta José Hierro, para terminar tomando un refrigerio en la zona de Puerto Chico, antes de nuestra cena en Brétema en Fisterra-Centro Gallego De Santander. Y, aunque lo hicimos personalmente, mostramos públicamente nuestra más sincera consideración a Pilar Ruiz de la Cuesta.
Nuestra tercera y última jornada estuvo marcada por la lluvia, los chubasqueros y los paraguas, comenzando por la obligada visita al Mercado de la Esperanza, los detalles internos de la catedral de Nuestra Señora de la Asunción y las exposiciones del Centro Botín, para concluir almorzando en el Restaurante Bahía. Tras un pequeño descanso realizamos un largo paseo hacia el Barrio Pesquero, donde pudimos degustar lo mejor del pescado y marisco de Cantabria.
Concluimos este pequeño resumen sobre la asamblea general 2024 con una selección de fotografías gracias a Josep María Navarro, nuestro reportero gráfico, habiendo elegido para ello un presentador de diapositivas en HTML5, que podemos visualizar en dispositivos móviles sin más que utilizar el dedo adelante o atrás para la transición de las mismas. Ahora bien, en un ordenador personal lo conseguiremos con las teclas o flechas de movimiento del cursor, pudiendo pulsar la tecla F (full) para el modo de pantalla completa.
El uso de este tipo de presentadores permite evitar la dependencia con presentadores comerciales como el PowerPoint de Microsofot o el KeyNote de Apple que, además, restringen la incorporación de algunos objetos diseñados en JavaScript, como las escenas interactivas de DescartesJS y GeoGebra, entre otros. Otra ventaja de usar HTML5 es poder compartir nuestras presentaciones vía web.
Si tienes interés en usar alguno de estos presentadores, te recomendamos el libro digital interactivo homónimo "Presentadores de diapositivas HTML5", donde encontrarás toda la información necesaria.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)

































 CONTACTO
CONTACTO
