Mostrando artículos por etiqueta: universidad
Título: Álgebra Lineal Interactiva (Vol. 1). Ejercicios y problemas. 2.ª edición
Sección: iCartesiLibri
Bloque: Álgebra
Unidad: Álgebra lineal
Nivel/Edad: 2º Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autor:Augusto Spela
ISBN: 978-84-10368-46-0
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Valor del dinero en el tiempo. Modelos y Aplicaciones. Parte segunda
Sección: iCartesiLibri
Bloque: Ciencias administrativas y económicas
Unidad: Finanzas
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autoras: José Benjamín Gallego Alzate
ISBN: 978-84-10368-45-3
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Química en la vida cotidiana: Desengrasantes y disolventes
Sección: iCartesiLibri
Bloque: Química
Unidad: Química
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autores: John Jairo García Mora y Margarita Emilia Patiño Jaramillo
ISBN: 978-84-10368-43-9
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Análisis matemático. Saberes básicos para Bachillerato LOMLOE.
Sección: iCartesiLibri
Bloque: Análisis Matemático
Unidad: Funciones, límites, derivación e integración
Nivel/Edad: 2º Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autores: José R. Galo Sánchez y María José García Cebrian
ISBN: 978-84-10368-37-8
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Física básica II
Sección: iCartesiLibri
Bloque: Física
Unidad: Física
Nivel/Edad: Bachillerato y Universidad (16 años o más)
Idioma: Castellano
Autor: Luis M. Castellanos y Roberto E. Lorduy
ISBN del volumen: 978-84-10368-36-1
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Cifras y letras
Sección: Miscelánea
Bloque: Juegos
Unidad: Juegos
Nivel/Edad: ESO/Bachillerato/Universidad/ 12 años o más
Idioma: Castellano
Autor: Luis Barrios Calmaestra
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
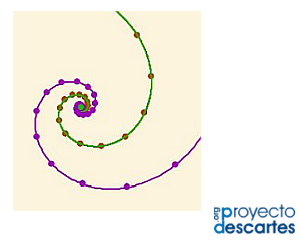
Título: Intepretando a Durero en su pseudoespiral
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad/ 18 años o más
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
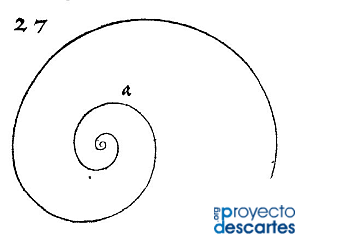
Título: Crítica de la pseudoespiral de Durero
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad/ 18 años o más
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Título: Métodos numéricos. Ejemplos prácticos con Matlab.
Sección: iCartesiLibri
Bloque: Análisis numérico
Unidad: Métodos numéricos
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autor: Elena E. Álvarez Saiz
ISBN: 978-84-10368-24-8
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Electrónica Digital. Ejemplos y Ejercicios. Segunda parte.
Sección: iCartesiLibri
Bloque: Ingeniería
Unidad: Electrónica
Nivel/Edad: Bachillerato y universidad (16 años o más)
Idioma: Castellano
Autores: Oscar Ignacio Botero Henao
ISBN: 978-84-10368-23-1
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)










 CONTACTO
CONTACTO
