 |
Repositorio de recursos educativos Departamento de Educación del Instituto de Matemáticas. UNAM (Universidad Nacional Autónoma de México). |
Materiales
ÁLGEBRANúmeros y operaciones |
Descarga |
||
 |
Divisibilidad
Concepto y ejemplos de criterios de divisibilidad. Se explora el concepto general y diversos criterios particulares de divisibilidad. El estudiante puede generar números aleatoriamente y explorar si es divisible por varios primos.
|
|
 |
Algoritmo de Euclides
Algoritmo de Euclides y su relación con el mcd y la congruencia. Se estudia el algoritmo de Euclides para calcular el máximo común divisor (MCD). Este último se usa en esta unidad didáctica para tres cosas: reducir una fracción; mostrar que si d=MCD(a,b), entonces se cumple que a≡b (mod d); y encontrar contraejemplos del recíproco de esta última afirmación, es decir: si a≡b (mod d), entonces d=MCD(a,b). |
|
 |
Cambio de base
Conteo y cambio de base entre bases decimal, binaria y hexadecimal. Lección que involucra inicialmente el conteo en diferentes bases y posteriormente aborda el cambio de base entre bases decimal, binaria y hexadecimal con distintas estrategias. |
|
 |
Sumando y restando en otras bases
Sumas y restas en binario y hexadecimal. Lección sobre el procedimiento de suma y resta en bases binaria y hexadecimal, y ejemplos de productos en hexadecimal. |
|
Ecuaciones algebraicas |
Descarga |
||
 |
Teorema Fundamental del Álgebra
Una aproximación a dos posibles demostraciones del Teorema Fundamental del Álgebra. Éstas se proporcionan a través del desarrollo de una intuición geométrica sobre el comportamiento de las raíces de un polinomio. |
|
Relaciones Algebraicas |
Descarga |
||
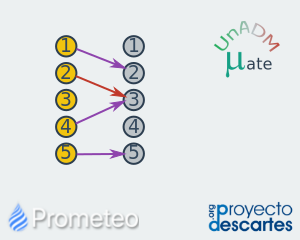 |
Relaciones
Relaciones, composiciones e identidades, así como propiedades de las relaciones. Se ilustran y definen los conceptos de relación, composición, identidad y asociatividad de relaciones y se definen propiedades básicas de Relaciones: reflexividad, simetría, transitividad. Se ilustra en formas interactiva la representación gráfica de una relación, la composición de relaciones.Se presenta una pequeña reseña de la importancia de las relaciones en numerosos ejemplos, incluyendo la industria, la computación, la vida cotidiana y, por supuesto, las matemáticas. |
|
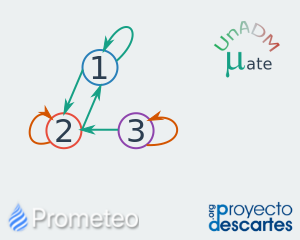 |
Relaciones de equivalencia
Análisis de las propiedades de las relaciones de equivalencia mediante interactivos. Se analiza con un modelo interactivo el estudio de las propiedades de relaciones de equivalencia e ilustrarlas con ejemplos. Se presenta una pequeña reseña de la importancia de las Relaciones de Equivalencia en las matemáticas. Se ilustran y definen los conceptos de reflexividad, simetría, transitividad, irreflexividad, antisimetría y relación de equivalencia y se muestra como computarlas en términos de la identidad la relacione inversa y la composición de relaciones. Se ilustra en forma interactiva, con su representación gráfica, la cerradura reflexiva, la cerradura simétrica y la cerradura transitiva de una relación. |
|
 |
Árboles y algoritmos
Conceptos y aplicaciones de teoría de grafos y aplicaciones diversas. En esta unidad se repasan conceptos básicos y se mencionan algunas aplicaciones de la teoría de gráficas, introduce los árboles, trabaja algunos ejemplos y se muestran algoritmos para determinar árboles recubridores de peso máximo y peso mínimo asociados a gráficas conexas sin lazos. |
|
Álgebra Lineal |
Descarga |
||
 |
Transformaciones lineales rígidas
Transformaciones lineales rígidas desde un abordaje de matrices. Se estudia la representación matricial de transformaciones lineales rígidas, i.e. Rotaciones, Proyecciones y Reflexiones, en dos dimensiones. El estudiante puede variar el ángulo de rotación, la pendiente de una recta, escoger un punto, un segmento, o un triángulo y ver gráficamente el efecto que esta transformación tiene, su representación matricial y las coordenadas de los puntos originales y sus transformados. |
|
 |
Ecuación general de las cónicas. Enfoque vectorial
Rotaciones y traslaciones de secciones cónicas a través de manejo de matrices. Unidad interactiva acerca de las herramientas del Álgebra Lineal y el tratamiento de las secciones cónicas de la Geometría Analítica. Respecto a la Geometría Analítica, el alumno podrá analizar los lugares geométricos de las cónicas para que a partir de la ecuación se determine la gráfica. En cuanto al Álgebra Lineal, el alumno utilizará matrices para la resolución de problemas. |
|
Lógica |
Descarga |
||
 |
Introducción a la lógica matemática
La lógica matemática, su lenguaje, notación y aplicaciones. Lección en dónde el usuario conocerá el lenguaje de la lógica matemática, y en particular el uso de las tablas de verdad, para demostrar diversos teoremas. |
|
ANÁLISISLímite y continuidad de funciones |
Descarga |
||
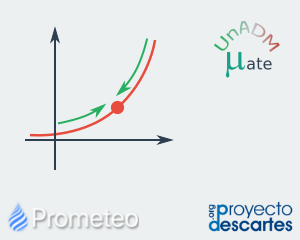 |
Definición formal del límite para Funciones Continuas
Presentación de la definición formal de límite. En esta unidad se presenta al alumno la definición formal del límite y su representación geométrica para funciones continuas, con la finalidad de que desarrolle una idea clara del significado de esta definición. |
|
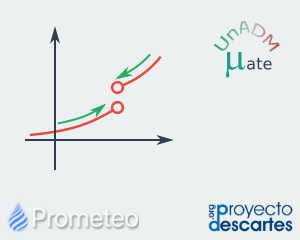 |
Definición formal de Límite y Funciones no Continuas
Funciones discontinuas. Sus tipos y propiedades y su relación con el límite. La definición de función continua está necesariamente ligada con el concepto de límite. Cuando una función no es continua, ¿qué pasa con el límite de la función en un punto donde dicha función no está definida? En esta unidad estudiamos los casos de funciones que son discontinuas a partir de que alguna de las hipótesis de la definición de función continua no se cumpla. |
|
Derivación de funciones |
Descarga |
||
 |
Gradiente
El gradiente y su interpretación como una generalización de la derivada multivariada. Lección en dónde se define el gradiente a partir del concepto de derivada direccional, así como también se muestra geométricamente su propiedad más importante: determinar máximos cambios en campos escalares o vectoriales. |
|
 |
Rotacional
El rotacional: su significado y aplicaciones. Lección en dónde se analiza el concepto de rotacional, su relación con el campo vectorial y su significado geométrico. |
|
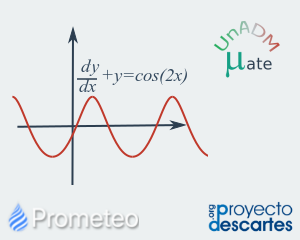 |
Ecuaciones diferenciales de primer orden I
Ecuaciones diferenciales y su aplicación en el modelado de problemas. Lección en donde, a través de la observación e interacción con ecuaciones de primer orden, se conoce qué tipo de ecuación se presenta y cómo se puede obtener su solución. |
|
 |
Ecuaciones diferenciales de primer orden II
Modelado de fenómenos a través de ecuaciones diferenciales. Lección en dónde se modela un fenómeno para poder predecir su futuro a partir de conocer sus características y cuáles son las reglas que gobiernan los cambios que ocurrirán. Se pretende que el usuario comprenda los pasos que siguen los investigadores para resolver problemas de la vida real usando ecuaciones diferenciales. |
|
 |
Ecuaciones diferenciales de segundo orden I
Solución numérica de Euler de ecuaciones diferenciales de segundo orden y de primer orden acopladas. Lección en dónde se utiliza el método de Euler para aproximar soluciones a un sistema de dos ecuaciones de primer orden extraídas de una ecuación de segundo orden. |
|
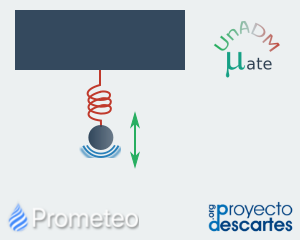 |
Ecuaciones diferenciales de segundo orden II
El oscilador armónico amortiguado como ejemplo de sistema con ecuación diferencial de segundo orden. Lección en donde se analiza el oscilador armónico junto con procedimientos matemáticos conocidos. Se analiza este modelo porque tiene numerosas aplicaciones en muchas ramas de la ciencia como la Mecánica, la Electrónica y la Física. Además es importante pues las ideas matemáticas utilizadas para resolverlo son muy atractivas. |
|
Representación gráfica de funciones |
Descarga |
||
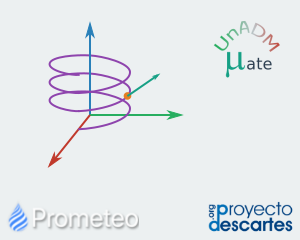 |
Curvas Paramétricas en el Espacio
Gráficas de curvas paramétricas en espacios tridimensionales. Esta unidad didáctica tiene como objetivo explorar la gráfica de una curva expresada paramétricamente en un espacio de tres dimensiones, así como distintas maneras de parametrizar una curva. |
|
GEOMETRÍAGeometría Analítica Tridimensional |
Descarga |
||
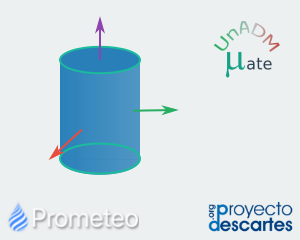 |
Coordenadas Cilíndricas y Esféricas
Sistemas de coordenadas cilíndrico y esférico con ejemplos. El objetivo de esta unidad didáctica es que el alumno conozca los sistemas de coordenadas cilíndricas y esféricas, que visualice la gráfica de la ecuación de algunas superficies dadas en estos sistemas de coordenadas en un espacio tridimensional y la manipule. |
|



