Anuncio de próxima publicación del libro "Gamificando con juegos AJDA"
Escrito por Jesús Manuel Muñoz Calle
Estamos ultimando y revisando el nuevo libro interactivo del Proyecto AJDA titulado "Gamificando con juegos AJDA" y que previsiblemente saldrá a la luz el próximo mes de junio de 2024.
- Aspectos básicos sobre gamificación.
- Liguilla de conocimientos.
- La conquista del futuro.
- Cazatesoros.
- Síntesis.
Día internacional de las mujeres en matemáticas
Escrito por José Antonio Salgueiro González
Desde el año 2019, el día 12 de mayo se viene celebrando en todo el mundo el "Día Internacional de las Mujeres en Matemáticas", coincidiendo con la fecha de nacimiento de la gran matemática iraní Maryam Mirzakhani, que fue la primera mujer en recibir la Medalla Fields, el máximo galardón que, con periodicidad cuatrienal, concede la Unión Matemática Internacional. Desgraciadamente, Maryam nos dejó a la temprana edad de 40 años, pero no lo hizo sin transmitir a la humanidad sus importantes aportaciones en el estudio de los espacios moduli de las superficies de Riemann y un gran legado.
Desde RED Descartes queremos sumarnos a esta importante efemérides y homenajear a todas las mujeres dedicadas al ámbito de las matemáticas, para lo que hemos realizado una humilde selección de recursos que compartimos y con los que te invitamos a conocerlas, descubrirlas o redescubrirlas.
| PUZLES INTERACTIVOS |
Trabajo Fin de Grado. Estado del arte del aprendizaje basado en juegos educativos digitales y diseño e implementación de métodos estadísticos de validación aplicados a GBL
Escrito por Jesús Manuel Muñoz Calle
En febrero de 2024, se ha presentado el Trabajo Fin de Grado de Ingeniería en Telecomunicaciones por D. José Manuel Candilejo Egea, titulado "Estado del arte del aprendizaje basado en juegos educativos digitales y diseño e implementación de métodos estadísticos de validación aplicados a GBL". Dicho trabajo se enmarca dentro de los Proyectos Gamifica y AJDA y puede consultarse de forma completa en el siguiente enlace.
El objetivo de este proyecto ha sido diseñar un sistema de validación estadística de plataformas tecnológicas de GBL, con la intención de poder aplicarse de forma sencilla y obtener unos resultados útiles para la valoración de sistemas gamificados de educación en desarrollo o incluso decisiones de adquisición de productos relacionados.
Para ello el trabajo se divide en dos grandes bloques, el primero es un análisis sistemático de los proyectos que se han realizado en el campo de la gamificación, enfocada en entornos tecnológicos, especialmente aplicados a la educación. A partir de las conclusiones que se obtengan de este análisis del estado del arte, se propondrá un modelo de validación y se realizará una prueba de este, lo que dará lugar al segundo bloque del proyecto.
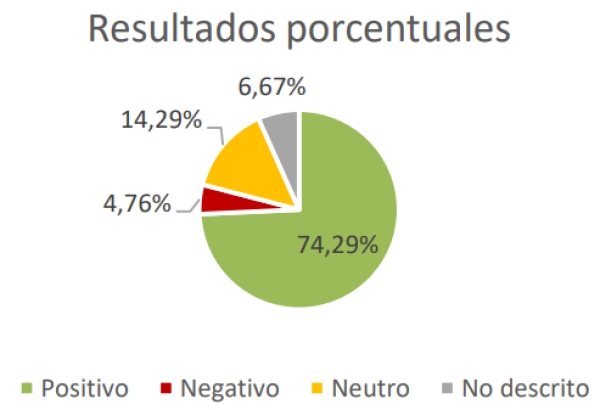
Se han buscado en las diferentes plataformas de publicaciones académicas artículos relacionados con experiencias empíricas con herramientas de gamificación digitales enfocadas en la educación. A través de términos relacionados se encontraron 1865 artículos que tras su lectura progresiva se fueron reduciendo hasta 100.
- Positivos: la experiencia habla concretamente de efectos positivos en uno o más de las dimensiones definidas anteriormente. Además, los otros campos no han sufrido alteraciones negativas, en todo caso, no varían con respecto al grupo de control o experiencias anteriores (permanecen neutros). Dentro de positivo, para añadir más granularidad se ha distinguido entre: ligeramente positivo, positivo y muy positivo.
- Neutros: no ha habido un incremento significativo en ninguno de los tres aspectos que se desean potenciar, tampoco ha habido efectos negativos.
- Negativos: algunos de los aspectos anteriores se han visto perjudicado por el experimento. Se ha distinguido, al igual que en los positivos entre: ligeramente negativo, negativo y muy negativo.
- No descrito: en el estudio no se especifica los resultados del experimento.
A. Bloque I
- La gamificación a través de plataformas digitales puede resultar beneficiosa si se aplica correctamente (74,9% de resultados positivos).
- 11 técnicas de gamificación distintas usadas, con resultados mayoritariamente positivos (siendo los quizzes la técnica con menor índice de éxito del 67,86%).
- La validación de los experimentos se realiza a través de métodos muy diversos, destacando entre ellos métodos que combinan distintos métodos, que se emplea en un 35% de los casos.
- La gamificación está considerablemente relacionada con las áreas de la educación, la telemática y las ciencias de la computación, el 70% de las revistas analizadas están dentro de este ámbito. • La metodología usada a la hora de gamificar tiene gran relevancia de cara a los resultados.
Jugando con las matemáticas. Día Internacional de las Matemáticas
Escrito por José Antonio Salgueiro González
En noviembre de 2019, la UNESCO proclamó el 14 de marzo de cada año como Día Internacional de las Matemáticas, con el fin de destacar el papel fundamental que desempeñan las ciencias matemáticas para hacer frente a los desafíos de nuestro tiempo en ámbitos como la inteligencia artificial, la salud, el cambio climático, la energía y el desarrollo sostenible y la mejora de la calidad de vida de la sociedad en general.
Para las personas que accedan por primera vez a esta información, debemos recordar que hemos venido celebrando desde hace años el conocido como "Día de π", una efemérides motivada por la forma de expresar la fecha diaria en el mundo anglosajón, es decir, 3/14, coincidiendo con las primeras cifras de este irracional número, considerado como una de las constantes matemáticas más importantes y conocidas.
"El tema de 2024, “Jugando con las matemáticas”, celebra los juegos matemáticos, puzzles y otras actividades lúdicas, pero también el “jugar” con las propias matemáticas, explorando, experimentando y descubriendo" (IMU).
Como el fin de RED Descartes es promover la renovación y cambio metodológico en los procesos de aprendizaje y enseñanza de las Matemáticas, y también en otras áreas de conocimiento, utilizando los recursos digitales interactivos generados con la herramienta de autor Descartes JS, hemos recopilado una humilde colección de objetos interactivos con los que, cualquier docente que no haya podido planificar este evento previamente para su aula, o cualquier alumno o alumna autodidacta, o en familia, puede participar desde un equipo tecnológico instalado en el aula o desde sus propios dispositivos móviles.
Puedes acceder sin más que pulsar sobre cada imagen y, en ciertos juegos, conviene leer la página de información.
| JUGANDO CON LAS MATEMÁTICAS DEL ... SUDOKU |
| JUGANDO CON LAS MATEMÁTICAS DE ... CAMUFLAR MONEDAS |
| JUGANDO CON LAS MATEMÁTICAS DE ... BUSCAR EL TESORO |
| JUGANDO CON LAS MATEMÁTICAS EN ... EL AULA |
| JUGANDO CON LAS MATEMÁTICAS CON ... OTROS RECURSOS |
Si no tienes suficiente con nuestra propuesta o buscas algo diferente, te recomendamos visitar los artículos de las ediciones anteriores:
- Día Internacional de las Matemáticas 2021
- Día Internacional de las Matemáticas 2022
- Día Internacional de las Matemáticas 2023
¡FELIZ DÍA INTERNACIONAL DE LAS MATEMÁTICAS!
Más...
Publicación del libro interactivo "Juegos didácticos. El Proyecto AJDA"
Escrito por Jesús Manuel Muñoz Calle
Tal y como anunciamos recientemente, en febrero de 2024 se ha publicado el libro interactivo titulado "Juegos didácticos. El Proyecto AJDA". Se puede acceder al mismo a través de las siguientes webs:
- Proyecto AJDA.
- Editorial iCartesiLibri de la Red Descartes.
- PubHTML5. Biblioteca de libros interactivos de la Red Descartes. (Estantería)
- Libros interactivos digitales. Universidad Autónoma de México (UNAM).
El nuevo libro sobre el Proyecto AJDA
Escrito por Jesús Manuel Muñoz Calle
- Aspectos generales de los juegos didácticos en educación.
- El Proyecto AJDA.
- Los juegos del Proyecto AJDA.
- Contenidos para juegos AJDA.
- Puesta en práctica en el aula.
- Investigación y retos del Proyecto AJDA.
Esperamos que el texto completo se publique próximamente, por lo que no vamos a hacer "spoiler".
Acceso
Lo más leído de lo publicado hace un mes
- Resumen estadístico anual de 2025 Visto 167 veces
- Opinión de ChatGPT sobre el Proyecto AJDA Visto 149 veces
- El universo del Mundo Mágico Visto 98 veces
CONTACTO
Canal Youtube
Calculadora Descartes
Versión 3.1 con estadística bidimensional
Código para embeber
Últimos Comentarios
-
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
