Mostrando artículos por etiqueta: Descartes
José Luis, ¡muchas felicidades en tu octogésimo cumpleaños!
Hoy es un día especial para José Luis Abreu León y también para todos sus colegas y amigos que integramos la Red Educativa Digital Descartes (RED Descartes). Él cumple ochenta años y nosotros llevamos veintiocho apoyándonos en la herramienta informática que supo vislumbrar y desarrollar con un único objetivo, el de mejorar la enseñanza de las Matemáticas. Supo mirar y ver lejos siendo pionero en el planteamiento de webs educativas interactivas, y nosotros pudimos auparnos a sus hombros para tratar de vislumbrar ese nuevo horizonte didáctico. Sí, esa herramienta fue ¡Descartes! y en base a ella se conformó un proyecto educativo el ¡Proyecto Descartes!, auspiciado inicialmente por el Ministerio de Educación de España y continuado desde el año 2013 por nuestra organización no gubernamental RED Descartes, de la que José Luis es socio fundador.
 |
 |
|
| Año 2004 (Expedición al Everest) | Año 2025 |
Descartes, fue la consecuencia o evolución de algunas ideas y desarrollos previos suyos que divulgó en el "Proyecto Prometeo", subtitulado como "Educación interactiva en la red" y que data del año 1997. Este proyecto se basaba en el desarrollo de NIPPES (Núcleos Interactivos Para Programas Educativos) que eran applets Java muy sencillos de configurar que permiten desarrollar interacciones con los datos más diversos[1].
 |
|
|
|
Escultura de Prometeo-Quetzalcóatl |
Avatar de José Luis |
Esos trabajos preliminares, José Luis, los sigue teniendo enlazados en su página de proyectos desarrollados; están en orden cronológico inverso al de su desarrollo por lo que hemos de desplazarnos al final de la página para llegar al citado proyecto Prometeo datado en 1997, a acceder a applets variados reaizados en 1997 y 1998, a ¡Descartes 1! en 1999 —web de presentación con ejemplos, documentación y aplicaciones—, o al de "Superficies" premiado por el Ministerio de Educación en el año 2000 —en este artículo de la revista SUMA se realiza una descripción de "Superficies"—, a Descartes 2, a Descartes 3, etc., que son ejemplos de una amplia lista de proyectos incluidos en la página citada y enlazada[2].
Pero, aquí, no es nuestro objetivo hacer una revisión del curriculum vitae de José Luis, quien previamente a su dedicación al desarrollo de software educativo inició su formación académica como físico teórico en la Facultad de Ciencias de la UNAM, se doctoró en Matemáticas en el Departamento de Matemáticas del M.I.T. y en su trabajo académico e investigador podemos destacar, como un hito, el haber sido director del Instituto de Investigación en Matemáticas Aplicadas y Sistemas (IIMAS) de la UNAM.
Son breves pinceladas de una vida dedicada a Ciencia y a la Educación tanto en México como en España. Pero lo más importante, al menos para los cartesianos de la RED Descartes, es que gracias al trabajo de José Luis muchos otros hemos podido enseñar, aprender e investigar las Matemáticas de una manera diferente y desarrollar objetos educativos interactivos que, con el apoyo inicial dado por el Ministerio de Educación de España y después desde nuestra organización no gubernamental, han permitido el aprendizaje a muchas, muchísimas personas en una amplia extensión mundial, con un gran foco ubicado en el mundo panhispánico.
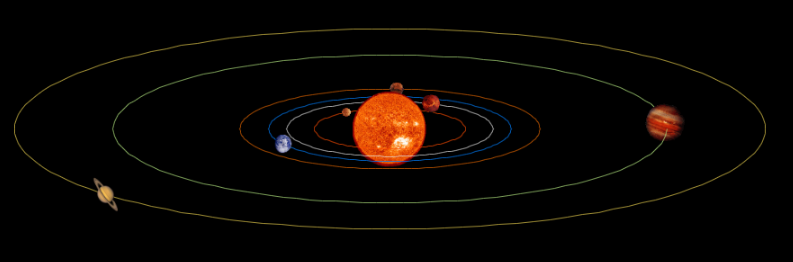
Son centenares las escenas interactivas con Descartes desarrolladas por José Luis, de las que podemos poner algunos ejemplos, pero destaquemos la siguiente por estar relacionada con el contexto de este artículo, el modelo heliocéntrico y el devenir de los planetas en su giro alrededor del sol... una vuelta, dos vueltas, tres vueltas,... ¡ochenta vueltas! has dado José Luis y te deseamos sigas incrementando el número de ellas durante mucho tiempo.
Los planetas, escena interactiva de José Luis Abreu León
Gracias José Luis por compartir tu saber y por habernos permitido estar sobre tus hombros, viendo más lejos.
¡Feliz inicio de tu novena década!
Un fuerte abrazo de tus colegas y amigos de RED Descartes.
[1]Desgraciadamente, por la caducidad que introduce la rápida evolución de la tecnología informática, en la actualidad los applets Java han pasado a ser funcionalmente inaccesibles en los navegadores ya que desde 2013 estos son bloqueados por cuestiones de seguridad, no son compatibles con el estándar actual HTML5. Por ello, si accede al Proyecto Prometeo citado, sólo observará una página de texto que nombra y describe objetos que no podrá ni ver, ni interactuar con ellos. Pero, afortunadamente, la informática suele obviar estos problemas con máquinas virtuales o simuladores y, gracias a nuestro colega cartesiano Francisco Rodríguez Villanego, hemos sabido que podemos instalar una extensión en los navegadores basados en Chrome (Chrome, Chromium, Brave, Edge, Opera, etc.) y proceder a activarla cuando accedamos al dominio que incluye los applets con los que queramos interactuar —permanecerá activa para ese dominio hasta que se desee desactivarla—. Esta máquina virtual intercepta el código Java que llega a la página, muestra la simulación y permite la interactividad. Se llama CheerpJ Applet Runner (https://cheerpj.com/cheerpj-applet-runner/). El navegador admite el código Java que recibe y lo interpreta porque no está realmente ejecutando Java, lo simula con otros lenguajes, y por ende es seguro. Así pues, le animamos a instalar esa extensión y que pueda gozar, o volver a gozar, a través de la manipulación de esos objetos educativos. Sólo añadir que, dependiendo de los recursos con los que cuente su ordenador, necesitará ser paciente y esperar a que la extensión termine de interpretarlos y los grafique.
[2] Si ya ha instalado la extensión CheerpJ Applet Runner en su navegador podrá ver las web de las versiones de Descartes, pero si lo desea también puede consultar las siguientes páginas que incluyen vídeos donde se muestran algunas características de Descartes 1, Descartes 2, Descartes 3, Descartes Álgebra, Descartes 4, que posteriormente dieron paso a Descartes 5 (con plug-in) y la versión actual DescartesJS compatible HTML5.
Documentación y vídeos del curso
"Diseño de libros interactivos con DescartesJS y herramientas de IA"
Recursos y tutoriales previos:

Los vídeos con la grabación de cada sesión del curso, que se imparte por videoconferencia según el calendario establecido, se irán publicando progresivamente a continuación:´
- Vídeo de la 1ª sesión (17 de octubre 2025). Presentación de la 1ª sesión.
- Vídeo de la 2ª sesión (31 de octubre 2025). Presentación de la 2ª sesión.
- Vídeo de la 3ª sesión (14 de noviembre 2025). Presentación de la 3ª sesión.
- Vídeo de la 4ª sesión (28 de noviembre 2025). Presentación de la 4ª sesión.
- Vídeo de la 5ª sesión (12 de diciembre 2025). Presentación de la 5ª sesión.
- Vídeo de la 6ª sesión (16 de enero 2026). Presentación de la 6ª sesión.
- Vídeo de la 7ª sesión (30 de enero 2026). Presentación de la 7ª sesión.
- Vídeo de la 8ª sesión (27 de febrero 2026).
Recursos ofrecidos durante la primera sesión
- Editores de texto plano
- Notepad++
- Sublime Text
- Phoenix Code
- Visual Studio
- Explicación sobre la instalación y uso de editores de texto plano para el libro interactivo
- En este video te explicamos cómo descargar y usar un editor de código para archivos HTML y CSS, necesario para editar los libros interactivos. Se incluyen dos editores adicionales: Sublime Text y Visual Studio.
- Tutoriales y manuales
- Diseño de libros interactivos (Segunda edición)
- Manual HTML5 (Una guía completa para dominar HTML desde cero)
- Manual CSS Manual CSS (Domina el diseño y estilo de tus páginas web)
- Manual de Visual Estudio Code (Guía completa para principiantes)
- Manual Phoenix Code (Guía completa para evitar errores y trabajar eficientemente)
- Manual Notepad++ (Guía completa para programar sin errores con Notepad++)
- Referencia de entidades HTML (Símbolos matemáticos, letras griegas,...)
- Manual de referencia KaTeX (Símbolos y funciones matemáticas para nuestros libros interactivos)
- ¿Qué debe contener el prefacio de un libro interactivo de RED Descartes? (Archivo PDF)
- Flujo de trabajo de la primera sesión (Archivo PPTX)
- Sobre Inteligencia Artificial
- Herramientas de IA para la enseñanza
- IA Generativas (Últimos desarrollos o actualizaciones)
- La importancia del prompt en la generación de imágenes con IA (Archivo PDF)
- Manual de usuario NotebookLM (Transforme la enseñanza con Inteligencia Artificial)
- Escritor de libros
Recursos ofrecidos durante la segunda sesión
- Tutoriales y manuales
- Flujo de trabajo de la segunda sesión (Archivo PPTX)
Recursos ofrecidos durante la tercera sesión
- Editores
- Tutoriales y manuales
Vídeos del curso "Diseño de objetos interactivos con DescartesJs e IA"
Presentación
Recursos y tutoriales previos:
- Descarga el software libre DescartesJS para tu sistema operativo
- Tutorial sobre DescartesJS - Nivel I
- Herramientas de Inteligencia Artificial para la enseñanza
- Lista en Youtube con vídeos de apoyo
- Descripción detallada de cada sesión

Los vídeos con la grabación de cada sesión del curso, que se imparte por videoconferencia según el calendario establecido, se irán publicando progresivamente a continuación:
- Vídeo de la 1ª sesión (11 de abril 2025). Presentación de la 1ª sesión. Resumen sesión 1.ª
- Vídeo de la 2ª sesión (25 abril 2025). Presentación de la 2ª sesión.
- Vídeo de la 3ª sesión (9 de mayo 2025). Presentación de la 3ª sesión.
- Vídeo de la 4ª sesión (23 de mayo 2025). Presentación de la 4ª sesión.
- Vídeo de la 5ª sesión (6 de junio 2025). Presentación de la 5ª sesión.
- Vídeo de la 6ª sesión (20 de junio de 2025). Presentación de la 6ª sesión.
- Vídeo de la 7ª sesión (4 de julio de 2025). Presentación de la 7ª sesión .
- Vídeo de la 8ª sesión (18 de julio de 2025).. Presentación de la 8ª sesión .

Vídeos del curso "Diseño de libros interactivos con IA y DescartesJS"
Vídeo de introducción
Recursos y tutoriales previos:
- Enlace a un archivo comprimido con la plantilla del libro. Las instrucciones se encuentran en el vídeo de bienvenida y presentación.
- Actividades previas a la primera sesión (19 minutos).
- Imágenes generadas por IA (5 minutos)
- Editores HTML (19 minutos)
- Contenido del curso y calendario:

Los vídeos con la grabación de cada sesión del curso, que se imparte por videoconferencia según el calendario establecido, se irán publicando progresivamente a continuación:
- Vídeo de la 1ª sesión (18 de octubre de 2024). Presentación de la 1ª sesión. Resumen sesión 1.ª
- Vídeo de la 2ª sesión (1 de noviembre de 2024). Presentación de la 2ª sesión.
- Vídeo de la 3ª sesión (15 de noviembre de 2024). Presentación de la 3ª sesión.
- Vídeo de la 4ª sesión (29 de noviembre de 2024). Presentación de la 4ª sesión.
- Vídeo de la 5ª sesión (13 de diciembre de 2024). Presentación de la 5ª sesión.
- Vídeo de la 6ª sesión (17 de enero de 2025). Presentación de la 6ª sesión .
- Vídeo de la 7ª sesión (7 de febrero de 2025). Presentación de la 7ª sesión .
- Vídeo de la 8ª sesión (14 de febrero de 2025).
|
Diseño de libros interactivos |
Vídeos de la quinta edición en línea del curso "Edición de libros interactivos"
Vídeo de introducción a la quinta edición en línea"
´- Vídeo de la 1ª sesión (13 de octubre de 2023). Presentación de la 1ª sesión.
- Vídeo de la 2ª sesión (27 de octubre de 2023). Presentación de la 2ª sesión.
- Vídeo de la 3ª sesión (10 de noviembre de 2023). Presentación de la 3ª sesión.
- Vídeo de la 4ª sesión (24 de noviembre de 2023). Presentación de la 4ª sesión.
- Vídeo de la 5ª sesión (8 de diciembre de 2023). Presentación de la 5ª sesión.
- Vídeo de la 6ª sesión (19 de enero de 2024). Presentación de la 6ª sesión.
- Vídeo de la 7ª sesión (2 de febrero de 2024). Presentación de la 7ª sesión.
- Vídeo de la 8ª sesión, sesión final del curso (16 de febrero de 2024).
"El deporte gallego tiene en el Centro Gallego de Tecnificación Deportiva (CGTD) la instalación de referencia de su excelencia competitiva, una excelencia que contempla también, por supuesto, la formación académica de los deportistas con la finalidad de conseguir su formación integral. "(Literalmente extraído de la web del CGTD). Pues bien, en este contexto se desarrolla la experiencia de aula que comparte nuestra compañera María del Carmen Quireza Ramos, profesora de matemáticas en bachillerato con deportistas de alto rendimiento.
El curso 2020-2021 ha pasado a la historia como aquel en el que se tuvieron que tomar medidas extraordinarias para seguir con las enseñanzas en los colegios e institutos. En este caso, el alumnado del CGTD constituye una extensión del IES Sánchez Cantón de Pontevedra, y sus aulas no fueron suficientes para atenderlos con las restricciones de distancia de seguridad obligatorias para evitar al máximo contagios del COVID 19.

Por ello, la Conselleria de Deportes, de la que depende la preparación deportiva de estos alumnos, tuvo a bien ofrecer unos espacios en el edificio de oficinas, salas de charlas del CGTD, para impartir clase a los grupos de 2º Bachillerato de ambas modalidades, como podemos apreciar en el mapa del recinto deportivo y académico. A esta situación tan excepcional, hay que añadir que la falta de internet al principio de curso y los fallos que se dieron a lo largo del mismo hicieron el trabajo muy complicado, tanto para profesorado como alumnado, resultando un curso muy complicado para impartir las clases utilizando los materiales de Descartes, especialmente los libros interactivos, como viene siendo habitual.

Como el alumnado se veía en la necesidad de usar sus datos móviles en los espacios asignados, la profesora elaboró unas pequeñas presentaciones con captura de pantalla de los materiales teóricos contenidos en los libros interactivos para la enseñanza en el aula, y más tarde, el alumnado consolidaba su aprendizaje conectándose a los libros interactivos desde la red de la residencia. Lo mismo ocurría cuando iban a competiciones, a concentraciones o estaban confinados en sus casas.
Se han utilizado, fundamentalmente, los siguientes recursos educativos abiertos en formato libro interactivo:
- Integrando con Paco
- Análisis matemático para bachillerato (Página 49. Regla de L'Hôpital)(Página 32. Derivabilidad. Rectas tangente y normal)(Página 9. Cálculo de límites)
- Geometría analítica del espacio

Los test para detectar posibles contagios se llevaban a cabo aleatoriamente y con mucha frecuencia en las mismas instalaciones del CGTD, y cuando se detectaba algún positivo, no sólo se iban él o ella confinados, sino todos los compañeros de su equipo de entrenamientos.
Ese curso fue un reto tanto para el alumnado como para la profesora. Se vieron en la necesidad de ser mucho más autónomos para sacar la mayor parte de los contenidos adelante y enfrentarse a la prueba de acceso a la universidad. A pesar de las dificultades, los resultados fueron buenos. Lo que más les gustó de los materiales era el poder hacer muchos ejercicios con la retroalimentación de los mismos, las explicaciones muy claras y concisas, y lo que menos que tardase tanto tiempo en cargar el material en los dispositivos, pero eso ya dependía más de la red.

La experiencia de impartir las clases de matemáticas a alumnos de alto rendimiento deportivo ha sido muy enriquecedora, al tener que trabajar de una manera diferente, centrándonos en lo importante, preguntando de otra forma lo mismo para los múltiples exámenes que nos vemos obligados a realizar, pues casi nunca tienes al grupo completo en el aula. El trato con el alumno es mucho más cercano y entre ellos ves mucho apoyo tanto a nivel deportivo como académico.
Novena y última sesión (24 de marzo de 2023)
|
1A.
|
En 2023 conmemoramos el veinticinco aniversario de Proyecto Descartes, una de las iniciativas más valiosas para conseguir una incorporación generalizada y eficiente de las TIC en el área de Matemáticas con nuevos procesos metodológicos. Por ello, desde RED Descartes estamos diseñando una serie de eventos y actividades con el objetivo de celebrar esta importante efemérides junto a nuestros socios, usuarios y seguidores de este proyecto educativo, a uno y otro lado de la mar océana.
Ha resultado ardua la tarea de sintetizar estos veinticinco años desde la aparición de la primera versión de la herramienta de autor Descartes, el proyecto educativo asociado y las acciones encaminadas para formar al profesorado, generar recursos educativos abiertos e interactivos que abarcan todas las etapas educativas (Infantil, Primaria, Secundaria y Universidad), experimentar y validar los recursos en el aula, incorporar mejoras, divulgar todos los aspectos del proyecto en encuentros, jornadas y congresos, desarrollar proyectos de colaboración escolar y constituir una red docente bien conectada.
Llegado el momento de recorrer históricamente un proyecto de semejante magnitud, debemos diferenciar perfectamente la etapa comprendida desde 1998 hasta 2013, como proyecto institucional del Ministerio de Educación, Cultura y Deporte de España, y la posterior a 2013, como organización no gubernamental sin ánimo de lucro.
Indudablemente, la mayor dificultad recae en la primera etapa, pues algunos ámbitos del proyecto ya no se encuentran publicados en la red de internet, han cambiado sus direcciones, existen enlaces rotos y un número importante de materiales obsoletos. No obstante, hemos podido recuperar algunos revisando nuestras unidades de almacenamiento y los CD y DVD publicados anualmente por CNICE (Centro Nacional de Información y Comunicación Educativa), ISFTIC (Instituto Superior de Formación y Recursos en Red para el Profesorado), ITE(Instituto de Tecnologías Educativas) y, ahora, INTEF, Instituto Nacional de Tecnologías Educativas y Formación del profesorado, aunque algún recurso mostrado no coincide fielmente con el original.
La dinámica y criterios seguidos han consistido básicamente en:
- Diseñar un recurso con la herramienta de autor DescartesJS.
- Seleccionar las acciones más significativas de cada año.
- Mostrar todos los aspectos del proyecto.
- Procurar la representatividad de todos los sectores de RED Descartes, tanto en España como en los países implicados.
- Mantener la máxima fidelidad histórica.
Ahora necesitábamos una herramienta visual para ordenar cronológicamente la historia de Proyecto Descartes durante este cuarto de siglo, y la inspiración llegó navegando por el libro interactivo "Cuarta revolución industrial. Fundamentos", que en una de sus páginas contiene una línea de tiempo interactiva dedicada a la historia del Metaverso.
Si navegas desde un PC puedes recorrer la línea de tiempo que hemos embebido en este mismo artículo. Pero si lo haces desde un dispositivo móvil, te recomendamos visitar línea de tiempo.
Octava sesión (10 de marzo de 2023)
|
1A.
|
Séptima sesión (24 de febrero de 2023)
|
1A.
|
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)







 CONTACTO
CONTACTO
