| |
|
Descarga |
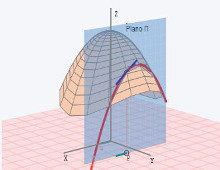 |
Interpretación geométrica de la derivada direccional
Miselánea
Dada una superficie y un punto se calcula la recta pendiente direccional en ese punto. Como caso particular se estudian las derivadas parciales al considerar como direcciones vectores directores de los ejes X e Y.
Área: Ciencias básicas - Cálculo de varias variables
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz |
 |
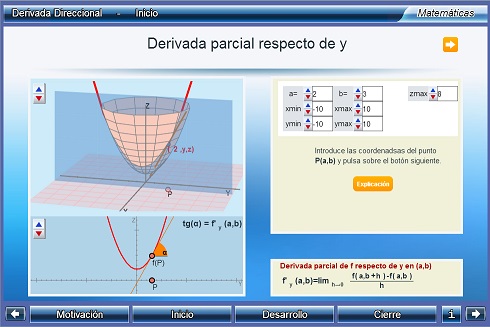 |
Derivada direccional
Unidad didáctica-Proyecto Un_100
Se introduce el concepto de derivada direccional. Asimismo, se muestran sus propiedades y su relación con el gradiente.
Área: Ciencias básicas - Cálculo de varias variables
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
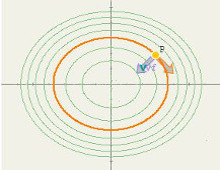 |
Gradiente y cuvas de nivel
Miscelánea
Dada una función z=f(x,y) las curvas de nivel son curvas planas. Para determinar la curva de nivel de f que pasa por (a,b) basta considerar la curva C de ecuación f(x,y)=k con k=f(a,b). Si se considera un vector tangente a esta curva este vector es ortogonal al gradiente de f en P.
La escena ayuda a comprobar la propiedad del gradiente de una función f en un punto P que afirma que es ortogonal a la curva de nivel que pasa por dicho punto.
Área: Ciencias básicas - Cálculo de varias variables
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz |
 |
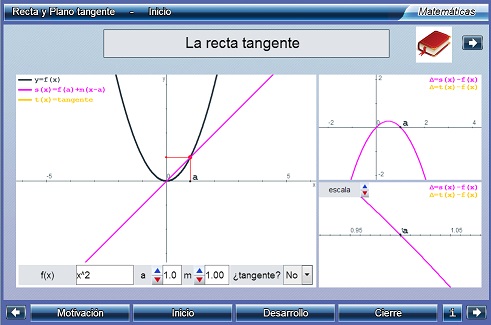 |
Recta y plano tangente
Unidad didáctica - Proyecto Un_100
Se definen:
a) La recta tangente a una función en un punto, como la recta que mejor se aproxima a dicha función en el entorno próximo a él, y se determina su ecuación. Se aborda el cálculo de derivadas.
b) El plano tangente a una superficie en un punto, como el plano que mejor se aproxima a dicha superficie en el entorno proximo a él. Se presentan tanto las derivadas parciales como las direccionales, y cómo calcular éstas a partir de las primeras.Se ve la relación existente entre continuidad, derivabilidad y diferenciabilidad. Se muestra que la existencia de todas las derivadas direccionales, no es suficiente para la existencia del plano tangente. Pero si existe éste, basta calcular las derivadas parciales.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: José R. Galo Sánchez |
 |
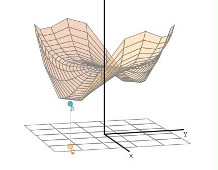 |
Extremos de funciones de dos variables. Método del hessiano.
Miscelánea
En esta aplicación Decartes se hace un estudio de los puntos criticos de una función real de dos variables, z=f(x,y). Se permite practicar en su búsqueda con la función que el usuario desee. Para ello, se ofrece un camino en tres pasos y una justificación teórica de los mismos basada en el metodo del hessiano.
.
Área: Ciencias básicas - Cálculo de varias variables
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz |
 |
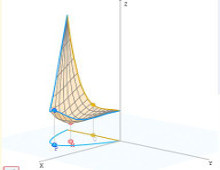 |
Extremos absolutos en una región cerrada y acotada
Miscelánea
En esta aplicación Descartes se propone la práctica del cálculo de los extremos absolutos de una función real de dos variables. Después de ver la definición de extremo absoluto, se puede practicar en una escena introduciendo la función objeto de estudio y su dominio.
Área: Ciencias básicas - Cálculo de varias variables
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
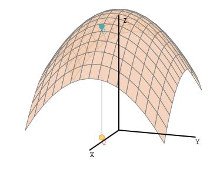 |
Extremos: multiplicadores de Lagrange
Miscelánea
En esta aplicación Descartes se propone la práctica del cálculo de los extremos de una función real de dos variables condicionados a una restricción sobre el dominio, G(x,y)=0. Después de repasar la definición de extremo condicionado se pasa a la escena en la que se pueden introducir tanto la función objeto de estudio, como la curva restricción.
Área: Ciencias básicas - Cálculo de varias variables
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
 |
Extremos de funciones de varias variables
Unidad didáctica - Proyecto Un_100
Se aborda el problema de encontrar los máximos y mínimos relativos de una función de varias variables. Se pretende:
- Introducir el método del hessiano para la clasificación de extremos de funciones de varias variables.
- Mostrar gráficamente la interpretacion del método de Lagrange para el cálculo de extremos condicionados en el caso de funciones de dos variables y una restricción.
Área: Ciencias básicas - Cálculo de varias variables
Nivel: Ingeniería y Tecnología
Autor: Varios autores. Editor: Elena E. Álvarez Sáiz |
 |
 |
El Teorema de Green y el planímetro
Unidad didáctica - Proyecto Un_100
En esta unidad se desarrollará el Teorema de Green desde un punto de vista geométrico y, mediante ejemplos, se mostrará su aplicación a distintos problemas, en particular, al funcionamiento de un planímetro, instrumento mecánico que permite calcular el área delimitada por una curva plana cerrada.
.
Área: Ciencias básicas - Cálculo de varias variables
Nivel: Ingeniería y Tecnología
Autor: Daniel Monsivais Velázquez |
 |