 |
Repositorio de recursos educativos Departamento de Educación del Instituto de Matemáticas. UNAM (Universidad Nacional Autónoma de México). |
Materiales
ÁLGEBRANúmeros y operaciones |
Descarga |
||
 |
Leyes de los exponentes y radicales
En esta lección sobre las leyes de los exponentes y radicales se aborda la notación con exponentes que simplifica operaciones con potencias de igual base. Se estudia el producto de potencias de igual base (cada una elevada a un exponente) y que consiste en sumar exponentes. También se aborda la potenciación de una base elevada a un exponente (que resulta en un exponente que es producto de los exponentes). Adicional-mente, se trata también el cociente de bases iguales aunque elevadas a exponentes que pueden ser distintos (que resulta en la sustracción de exponentes del numerador menos el del denominador). Y finalmente se trata también la extracción de raíces, o radicación, de bases elevadas a un determinado exponente (que resulta en un exponente fraccionario para la base compuesto por el exponente de la base entre el índice del radical de la raíz). Se deducen estas reglas con el objeto de que el alumno, en caso de no recordarlas, pueda contar con ellas recordando dicha deduc-ción. Adicionalmente, se presentan varios ejercicios en que puede poner en práctica las reglas antes mencionadas y cinco preguntas de autoevaluación. |
|
Expresiones algebraicas |
Descarga |
||
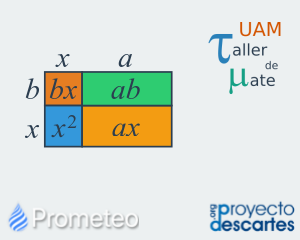 |
Productos notables
Se presentan los productos notables del tipo binomio al cuadrado o cuadrado perfecto y binomio conjugado. Los productos notables se introducen al mostrar lo que sucede al multiplicar algunos productos especiales (notables) y analizando el resultado obtenido. Se presentan ejercicios para reafirmar la noción de producto notable, permitiendo al alumno la construcción de esquemas para fijar el concepto abstracto de un producto notable. Además, se presentan ejercicios de tipo numérico para practicar la aplicación de los conceptos estudiados. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
Ecuaciones y sistemas |
Descarga |
||
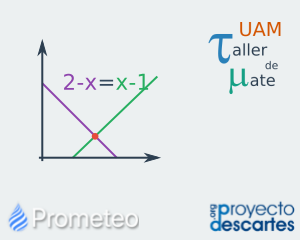 |
Ecuaciones de primer grado con una incógnita
Se abordan las ecuaciones de primer grado con una incógnita o variable con énfasis en que el obtener la solución se puede hacer de forma dirigida (algebraicamente). La obtención de la solución de forma dirigida se hace en contraposición con la alternativa al método de prueba y error. Se hace la analogía entre la solución de una ecuación compuesta por dos rectas con la obtención de una de las coordenadas del punto de inter-sección de las mismas. Adicionalmente, incluye ejercicios propuestos para que el alumno practique, y cuya retroalimentación involucra un detallado manejo de los despejes para obtener la variable o incógnita en cuestión. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
 |
Aplicaciones de las ecuaciones de primer grado con una incógnita
Se presentan problemas de aplicación de las ecuaciones de primer grado con una incógnita abordadas en la unidad 'Ecuaciones de primer grado con una incógnita'. Más que abordar los métodos de solución, esta unidad se dedica a orientar al alumno a pasar del problema planteado con palabras a su representación matemática. Asimismo, se hace énfasis en la ubicación de inconsistencias en problemas que, aunque bien puedan tener solución matemáticamente hablando, no tienen solución en el contexto del problema. Al final del recurso, se proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
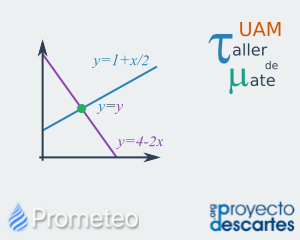 |
Solución de problemas por medio de sistemas de ecuaciones
Representación de problemas mediante sistemas de ecuaciones lineales y su solución. En esta lección se explica cómo se pueden representar diversos problemas a través de sistemas de ecuación lineales y cómo la solución de éstos nos permite obtener también la solución al problema planteado. Adicionalmente, se presentan varios ejercicios en donde el usuario puede poner en práctica los conceptos aprendidos. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
 |
La ecuación cuadrática y sus métodos de solución
En esta unidad se presenta la ecuación cuadrática y los diversos métodos para obtener sus soluciones. Se abordan, para cuando es posible, los métodos de factorización y despeje directo para obtener las soluciones de la misma. Para ecuaciones en donde dicho abordaje no es costeable, se deduce la fórmula general de la ecuación cuadrática. Se hace una breve introducción al discriminante y a su efecto en el número de soluciones. Se hace una breve relación entre la ecuación cuadrática y sus soluciones y la ecuación de una parábola vertical para que la transición de soluciones a raíces de la misma sea más fácil. Para ejercitar lo aprendido, se presentan ejercicios al estudiante en que ha de calcular las soluciones a una cuadrática siguiendo el método indicado en el problema. Con el fin de proporcionar una autoevaluación, se presentan cinco preguntas de al alumno que involucran el discriminante, el número de soluciones y las soluciones como tal. |
|
 |
Solución a problemas con ecuaciones de segundo grado
Ejercicios de aplicación que involucran ecuaciones de segundo grado. Esta unidad complementa los temas revisados en unidades previas sobre la ecuación cuadrática y la parábola vertical con el abordaje de una variedad de ejercicios de aplicación. Se enfatiza que cualquier problema que pueda ser modelado por una ecuación que puede llevarse a una forma cuadrática es candidato a ser resuelto por la fórmula general de la ecuación cuadrática. Se presentan algunos problemas en que no es inmediato que el modelo del mismo será una ecuación cuadrática. No obstante, ello resulta ser así como se muestra en la solución paso a paso del mismo. Para practicar lo aprendido en esta y otras unidades relacionadas con el tema, se presentan varios ejercicios en los que el alumno ha de proporcionar la respuesta y recibe retroalimentación en caso de errar. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
Inecuaciones y sistemas |
Descarga |
||
 |
Solución gráfica de desigualdades lineales
El recurso estudia las desigualdades lineales, mostrando los métodos de resolución algebraico y gráfico. Se hace énfasis en el método de resolución gráfico al ser más intuitivo. Se presentan ejercicios para determinar la solución de desigualdades lineales, utilizando el método de resolución gráfico. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
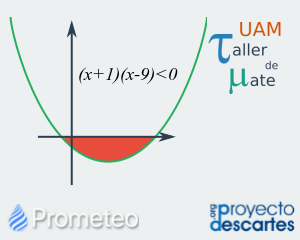 |
Solución gráfica de desigualdades cuadráticas
Ecuaciones cuadráticas y su solución por dos métodos distintos. Esta lección aborda las desigualdades cuadráticas y cómo se pueden resolver. Se muestra el método del diagrama de signos y el método de la comparación de ecuaciones. Adicionalmente, se presenta un ejercicio de solución de desigualdades cuadráticas mediante el diagrama de signos, seguido de un ejercicio de aplicación donde se muestra cómo un problema físico se puede resolver mediante ecuaciones cuadráticas. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
ANÁLISISFunciones elementales |
Descarga |
||
 |
La parábola vertical
Se aborda la parábola vertical, sus propiedades geométricas y puntos y rectas relacionados. Se deduce su ecuación ordinaria a partir de la condición de que sus puntos equidistan lo mismo de un punto llamado 'foco' que de una recta (la directriz), que ha de ser horizontal por tratarse en este caso de una parábola vertical. Se introducen los conceptos de foco, vértice y directriz. Se analiza también la propiedad de enfoque de la parábola y su utilidad en la construcción de antenas parabólicas. En los ejercicios se presentan casos del paso de la forma ordinaria de la ecuación a la general y viceversa. Por último, se presentan cinco preguntas de opción múltiple para evaluar el aprendizaje y grado de dominio de los conceptos abordados en la unidad. |
|
 |
Representación gráfica de la parábola. Apertura, intersecciones con el eje Y y vértice
Esta unidad aborda el vértice de las parábolas verticales considerando como su coordenada horizontal el punto medio de las raíces (sean estas reales o complejas). A partir de la coordenada horizontal del vértice, se obtiene la vertical. Así pues, muestra una forma alternativa a completar el cuadrado para calcular las coordenadas de dicho punto. Por otra parte, también se deducen las coordenadas de la intersección de una parábola vertical con el eje de las ordenadas. Un último parámetro que se incluye es el lado recto como una forma de cuantificar la apertura de una parábola. Se hace explícita la relación de el lado recto con el coeficiente de x cuadrada en la forma desarrollada de la función de la parábola. Se presenta una parte de ejercicios, tanto teóricos como de aplicación, para que el alumno ponga en práctica lo aprendido. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
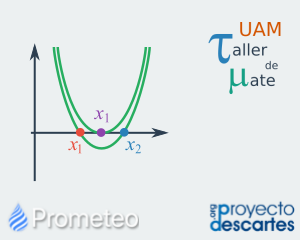 |
Interpretación de la existencia de raíces reales en la función cuadrática
Análisis de la existencia de raíces de la ecuación cuadrática a partir del discriminante. Esta unidad se aboca a la interpretación de la existencia (única o dual) o inexistencia de soluciones reales en una ecuación cuadrática a partir de análisis del discriminante en la fórmula general de la misma. Se extiende este conocimiento a las funciones cuadráticas y se muestra la contraparte gráfica de esta existencia o inexistencia de soluciones como la existencia o inexistencia de raíces de la función cuadrática. Se presentan ejercicios de determinación del número de raíces en una función cuadrática y del cálculo (en caso de existir) de las mismas. Se concluye con cinco preguntas de autoevaluación sobre el tema. |
|
 |
La circunferencia y sus propiedades
Deducción de las ecuaciones ordinaria y general de la circunferencia a partir de su definición geométrica. En esta unidad sobre la circunferencia y sus propiedades se presenta a la misma como el conjunto de puntos equidistantes al centro. Se hace la deducción de la ecuación ordinaria de la circunferencia y, mediante expansión de ella, de la ecuación general de la misma. Adicionalmente, se ilustra el paso de una forma a la otra. Mediante análisis de la ecuación ordinaria, se presenta una forma de encontrar las coordenadas del centro y el radio de una circunferencia. Se presentan algunas propiedades de la circunferencia adicionales como el ángulo recto formado por un triángulo inscrito en la circunferencia cuando un lado coincide con un diámetro, así como el cuadrilátero cíclico. Se incluyen ejercicios no aplicados y de aplicación con retroalimentación detallada de la solución. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
GEOMETRÍAGeometría analítica plana |
Descarga |
||
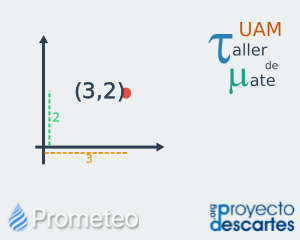 |
El plano cartesiano
El recurso introduce los conceptos básicos del plano cartesiano como sistema de referencia para la ubicación de elementos geométricos en un espacio bidimensional. Se ofrecen diversos ejercicios que permiten la exploración y el análisis del plano cartesiano, así como sus elementos básicos (los puntos). Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
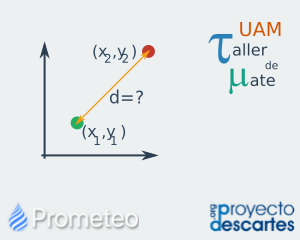 |
Distancia entre dos puntos
Se trata el problema de medir la distancia entre dos puntos, desde la deducción hasta su profundización en la tercera dimensión. Se presenta de manera incremental la deducción del concepto, mostrando primero lo que ocurre sobre la recta numérica, profundizando después sobre el plano cartesiano y por último dando el resultado para tres dimensiones. Se cuenta con una escena interactiva que muestra el cálculo de la distancia entre dos puntos sobre el plano cartesiano, permitiendo al alumno mover los puntos libremente y observar los cálculos realizados para obtener la distancia. Además, se cuenta con ejercicios que requieren que el alumno realice los cálculos de la distancia a partir de las coordenadas de dos puntos. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
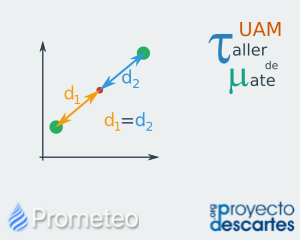 |
Coordenadas del punto medio
Se presenta el cálculo de las coordenadas del punto medio entre dos puntos, primero el concepto sobre la recta numérica y después sobre el plano cartesiano. Se cuenta con una escena interactiva que permite observar el cálculo de las coordenadas del punto medio entre dos puntos sobre el plano cartesiano, permitiendo al alumno mover los puntos libremente y observar cómo se obtienen las coordenadas de un punto medio. Además, se cuenta con ejercicios que requieren que el alumno realice los cálculos de las coordenadas de un punto medio entre dos puntos. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
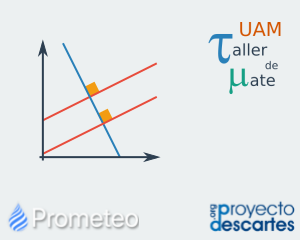 |
Paralelismo y perpendicularidad
Los criterios de paralelismo y perpendicularidad entre rectas a partir de sus pendientes. Esta unidad trata sobre los conceptos de rectas paralelas y perpendiculares. Inicia con un repaso de los parámetros que caracterizan a las rectas (pendiente y ordenada al origen). Posteriormente se identifica la pendiente como el parámetro que define si una recta es paralela o perpendicular a otra, y las características que debe cumplir para ser una u otra. Se enfatizan dichas características a partir de la fórmula para la pendiente entre rectas. Se incluyen ejercicios para que el alumno practique, algunos de los cuales son de aplicación en geometría. Se ejercita, asimismo, con problemas que implican obtener una recta perpendicular o paralela a otra y que pasa por un punto determinado. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
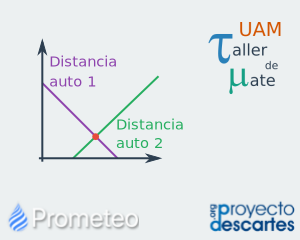 |
Intersección de rectas
Problemas que se pueden representar con ecuaciones de primer grado y su solución. Como continuación de unidades sobre las rectas y sus parámetros, esta unidad orienta al alumno a analizar problemas de palabra que involucran rectas para expresarlos en lenguaje matemático y así poder resolverlos. Recapitula, asimismo, sobre conceptos importantes relacionados con la solución de un sistema de ecuaciones de primer grado. También identifica nuevamente a las coordenadas del punto de intersección de rectas como la solución del problema en cuestión. Orienta al alumno también a identificar problemas cuyo planteamiento no implica una solución real (aun cuando la haya matemáticamente hablando). Se incluye una parte de ejercicios cuya retroalimentación guía al alumno al correcto planteamiento y solución de una ecuación a partir de las condiciones del problema. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
Geometría plana |
Descarga |
||
 |
Triángulos semejantes
Criterios de semejanza y congruencia de triángulos y la relación entre semejanza y proporcionalidad. En esta unidad sobre triángulos semejantes se abordan los criterios que hacen que dos triángulos sean congruentes y, en el caso general, semejantes. Se presta especial atención a los criterios mínimos para establecer semejanza entre triángulos. Se enfatiza que dos triángulos pueden ser semejantes bajo estos criterios independientemente de rotaciones, traslaciones, y cambios de proporción. Por otra parte, se ponen de manifiesto las propiedades de proporciones de lados correspondientes de triángulos semejantes. Estas propiedades se usan para la resolución de problemas que involucran triángulos semejantes. Estos problemas (de aplicación y no aplicados) son abordados en las secciones de ejercicios. Se presentan, asimismo, cinco preguntas de autoevaluación. |
|
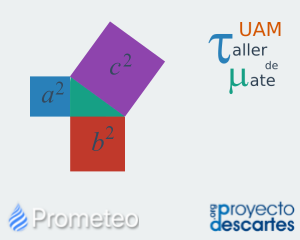 |
Teorema de Pitágoras
Demostración y aplicaciones del teorema de Pitágoras. En esta lección se aborda el teorema de Pitágoras. Se inicia con una nota histórica, a continuación, se hace una demostración de dicho teorema y ejemplos numéricos para ver cómo se cumple. También se hace una explicación de los usos prácticos de este teorema y para finalizar se hacen 5 preguntas con base en el desarrollo de la unidad. |
|
Trigonomería |
Descarga |
||
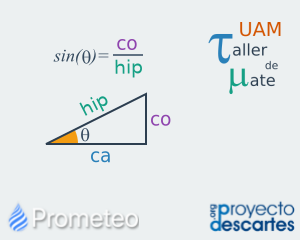 |
Razones trigonométricas
En esta lección sobre razones trigonométricas se explica de dónde provienen las razones trigonométricas, cuáles son las razones más importantes y cuáles son sus inversas. Se explica cómo se pueden obtener los valores de dichas funciones y también se explica cuáles son las razones de ángulos suplementarios, complementarios y opuestos. Se ofrecen ejercicios para que el alumno practique lo aprendido y, al final del recurso, se proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
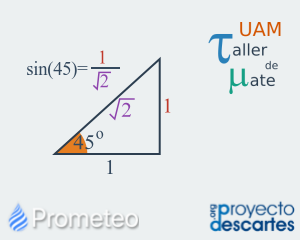 |
Funciones trigonométricas de ángulos notables
Deducción de valores de funciones trigonométricas para ángulos notables y su utilidad. Esta lección trata sobre las funciones trigonométricas de ángulos notables. Primero se le muestra al usuario cuáles son los ángulos notables y por qué se les llama así. A continuación, se muestra el procedimiento geométrico para obtener estos ángulos a partir de triángulos rectángulos especiales. Finalmente se muestra cómo se obtiene el valor de las funciones trigonométricas de estos ángulos notables con el precedente de que el usuario conoce las definiciones de las razones trigonométricas. Se ofrece un ejercicio para que el alumno ejercite lo aprendido y, por último, se proporcionan 5 preguntas de opción múltiple para verificar que los conceptos hayan sido aprendidos. |
|
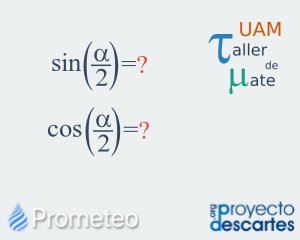 |
Identidades trigonométricas
Deducción y aplicaciones de las fórmulas trigonométricas para resta y suma de ángulos, y del ángulo doble y medio. En esta unidad se aborda la relación Pitagórica. A partir de ésta, y de los conceptos de funciones pares e impares, se deduce la fórmula del coseno de la resta de ángulos, a partir de la cual se deducen el coseno de la suma de ángulos, el seno de la resta y suma de ángulos, la tangente de la resta y suma de ángulos, así como las fórmulas trigonométricas del ángulo doble y del ángulo medio. Se incluyen ejercicios que involucran simplificación de expresiones y el cálculo de razones trigonométricas para ángulos que no son notables, pero que pueden expresarse en función de ángulos notables. Asimismo, se incluyen ejercicios de aplicación. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
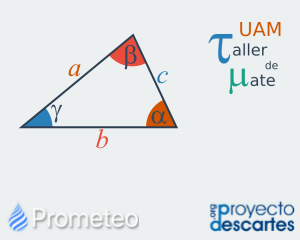 |
Ley de los senos y los cosenos
Demostración y aplicaciones de la ley de senos y cosenos para el cálculo de lados y ángulos de triángulos no rectángulos. En esta unidad sobre las leyes de senos y cosenos se aborda el caso de triángulos no necesariamente rectángulos. De estos triángulos se suelen conocer, por ejemplo, los 3 lados, o un par de ángulos internos y el lado opuesto a alguno de ellos, o dos lados y un ángulo opuesto a alguno de ellos. A partir del teorema de Pitágoras y algunas identidades trigonométricas se realiza la deducción de la ley de cosenos, la cual se expresa como una generalización del teorema de Pitágoras a triángulos no rectángulos. Por otra parte, a partir del argumento de conservación de áreas de triángulos independientemente de la base elegida se realiza la deducción de la ley de senos. En la parte de ejercicios se pone de manifiesto la utilidad de estas dos leyes en la solución de problemas tanto teóricos como de aplicación, y se da la oportunidad al alumno de ejercitar lo aprendido. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|
 |
Aplicaciones diversas que se resuelven usando triángulos y funciones trigonométricas
Aplicación de los temas sobre triángulos vistos en otras unidades a la solución de problemas y elección de estrategias de solución. Esta unidad consiste en un repaso de lo visto en unidades anteriores sobre el Teorema de Pitágoras, semejanza de triángulos, trigonometría y las leyes de senos y cosenos. No obstante, la presente unidad también pretende orientar al alumno a elegir, de una multitud de caminos posible para resolver un problema dado, el abordaje que resulta más eficiente. Es decir, se aboca a que el alumno practique la identificación del método de solución más directo para un problema. En la parte de desarrollo se incluyen problemas para los cuales se muestra la estrategia más útil, así como la solución de cada problema. Posteriormente, en la parte de ejercicios, el alumno ha de indicar cuál es la estrategia más directa y además resolver un problema. La estrategia de solución y solución misma al problema se presenta en caso de que el alumno erre varias veces. Por último, el recurso proporciona una breve autoevaluación que consta de cinco preguntas de opción múltiple, para valorar que los conceptos del recurso han sido comprendidos. |
|



