| |
|
Descarga |
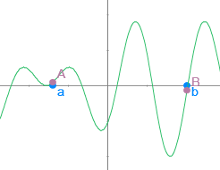 |
Teorema de Bolzano. Método de la bisección
Miscelánea
Escena interactiva donde, además de repasar el Teorema de Bolzano, se puede practicar el método de la bisección, basado en dicho teorema. Este método permite obtener un valor aproximado de los puntos de corte con el eje OX de una función o, lo que es lo mismo, la aproximación sucesiva de las raíces de una ecuación.
Área: Métodos numéricos
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
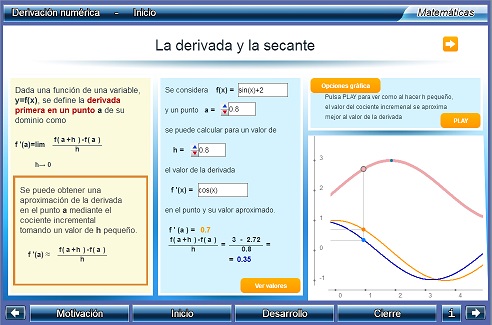 |
Derivación numérica
Unidad didáctica - Proyecto Un_100
Los objetivos de la unidad son los siguientes:
- mostrar diferentes fórmulas de derivacion numérica (diferencias progresivas, regresivas y centradas) justificando su validez a partir de desarrollos en serie de Taylor.
- analizar el error de la aproximación numérica de la derivada en un punto cuando se utilizan estas fórmulas.
Área: Métodos numéricos
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz |
 |
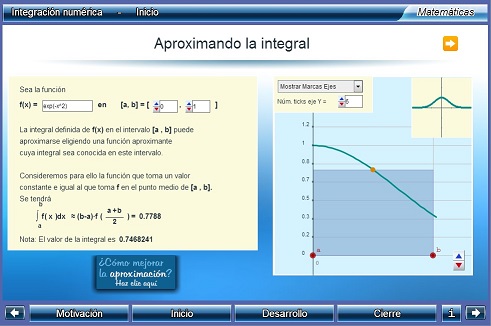 |
Integración numérica
Unidad didáctica - Proyecto Un_100
En esta unidad se pretende:
- aproximar una integral definida utilizando la regla del trapecio
- aproximar una integral definida utilizando la regla de Simpson
- analizar los errores de aproximación en la regla del trapecio y en la regla de Simpson Área: Métodos numéricos
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz |
 |
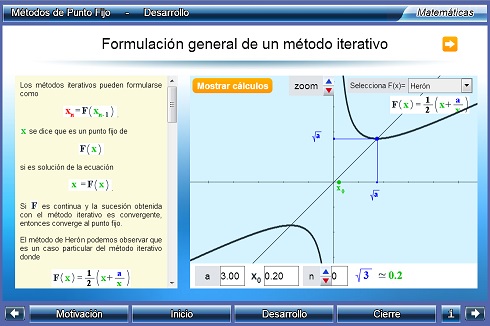 |
Métodos del punto fijo
Unidad didáctica - Proyecto Un_100
Se introducen los métodos iterativos para la resolución de ecuaciones no lineales y se analiza cómo pueden construirse. Asimismo, se muestran ejemplos de convergencia monótona, convergencia oscilante, divergencia monótona y divergencia oscilante. Por último, se presenta la generalización de la construcción de estos métodos de punto fijo, y se comprueba que el de Newton es un caso particular de los mismos
.
Área: Métodos numéricos
Nivel: Ingeniería y Tecnología
Autor: José R. Galo Sánchez |
 |
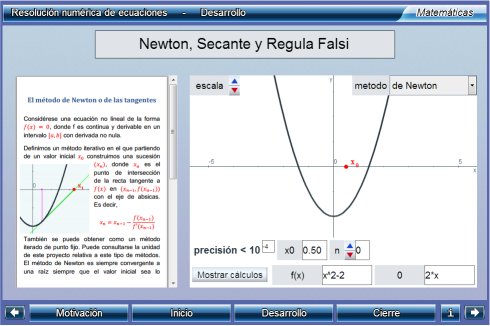 |
Resolución numérica de ecuaciones
Unidad didáctica - Proyecto Un_100
Resolver una ecuaciónn f(x)=0 es determinar aquellos valores que verifican esa igualdad. La teoría de Galois muestra cómo las ecuaciones polinómicas --las que podemos considerar como las más sencillas al intervenir sólo sumas, restas y multiplicaciones-- de grado mayor o igual que cinco no son resolubres por radicales, es decir, que no puede encontrarse una expresión algebráica que permita calcular sus raíces. Por tanto sólo sabemos como resolver unos pocos tipos de una infinidad de ecuaciones. Es necesario proceder a determinar soluciones aproximadas con una precisión deseada y para ello se utilizan metodos iterativos que a partir de un valor inicial se construye una sucesión de valores que converja a una solución. En esta unidad se busca aprender los siguientes métodos iterativos para la resolución de ecuaciones:
a) Método de la bisección
b) Método de la Secante
c) Método de la Regula Falsi
d) Método de Newton .
Área: Métodos numéricos
Nivel: Ingeniería y Tecnología
Autor: José R. Galo Sánchez |
 |
 |
Simulador de sistemas autónomos y no autónomos
Miscelánea
Simulador de sistemas diferenciales autónomos y no autónomos. Se contemplan dos modos de trabajo: ejemplo --sistemas predefinidos-- y edición --sistemas definidos por el usuario--. Para cada sistema se visualiza en el Plano de Fase el campo vectorial o direccional y la órbita solución del sistema dinámico para las condiciones iniciales y lapso de tiempo de observación elegidos; mientras que en el Plano de las Series de Tiempo muestra el comportamiento de las variables de estado>
.
Área: Métodos numéricos
Nivel: Ingeniería y Tecnología
Autora: Valeria Bertossi |
 |