| |
|
Descarga |
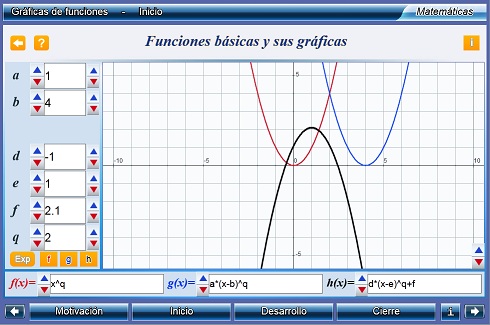 |
Gráficas de funciones
Unidad didáctica - Proyecto Un_100
El objetivo de la unidad es presentar al alumno el concepto de graficación de una función. Mediante la unidad, podrá graficar funciones de su elección. Se permite al alumno graficar más de una función simultáneamente y se cuentan con pulsadores que representan parámetros que el alumno puede incluir en sus funciones, de tal suerte que pueda observar el efecto de tales parámetros al variarlos. Esta unidad puede aprovecharse, por ejemplo, para ilustrar el concepto de 'recta tangente' a una curva en un punto al graficar la función y su primera derivada.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Leticia Montserrat Vargas Rocha y José Luis Abreu León |
 |
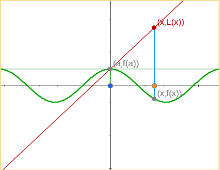 |
Derivada - aproximación lineal
Miscelánea
Escena interactiva que permite caracterizar la recta punto pendiente.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
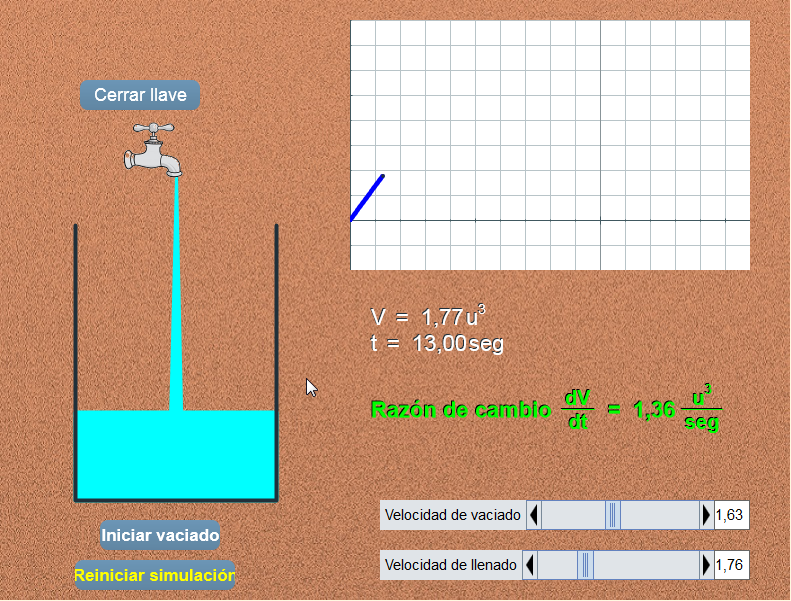 |
La derivada como razón de cambio
Miscelánea
Simulador en el que se proponen dos actividades que permiten comprender la derivada como razón de cambio.
.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Juan Guillermo Rivera Berrío y Carlos Alirio Ballesteros Torres |
 |
 |
Derivadas de funciones elementales
Miscelánea
Escena que, gracias a la aleatoriedad, incluye una multitud de ejercicios de derivadas elementales y su generalización a través de la regla de la cadena.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Consolación Ruiz Gil
|
 |
 |
Regla de la cadena - derivadas
Miscelánea
Escena que, gracias a la aleatoriedad, incluye una multitud de ejercicios de derivadas, para aplicar la regla de la cadena.
.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Miguel Ángel Cabezón Ochoa |
 |
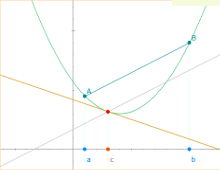 |
Teorema del valor medio
Miscelánea
Escena interactiva donde se enuncian las hipótesis y tesis del Teorema del Valor Medio.
En la gráfica se plasma el sentido geométrico del mismo.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
 |
Cálculo diferencial
Libro digital interactivo - iCartesiLibri
Cerca de 90 discursos de Descartes, diseñados por cartesianos mexicanos, españoles y colombianos, que adentran en los fundamentos del Cálculo infinitesimal, la razón de cambio y su aplicación en la modelación matemática del mundo físico.
.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Varios autores. Editor: Juan Guillermo Rivera Berrío
ISBN 978-958-99249-6-9
|
 |
 |
Cálculo diferencial
Libro digital interactivo - iCartesiLibri
Segunda edición del libro "Cálculo diferencial", ahora en formato flip book. Incluye nuevos objetos interactivos de aprendizaje, vídeos, simulaciones, animaciones e imágenes.
.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Varios autores. Editor: Juan Guillermo Rivera Berrío
ISBN 978-958-99249-6-9
|
 |
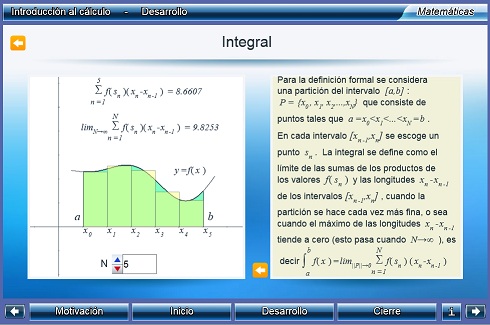 |
Introducción al cálculo
Unidad didáctica - Proyecto Un_100
El objetivo de esta unidad es presentar al alumno los tres conceptos fundamentales del cálculo: el límite, la derivada y la integral, y el teorema fundamental del cálculo. El alumno podrá experimentar con los interactivos observando que el cálculo se basa en problemas de resolver límites, ya sea el límite de la suma de polígonos para el caso de la integral, o el límite de la pendiente de dos puntos arbitrariamente cercanos en una curva, para la derivada. Se explica que el teorema fundamental del cálculo permite relacionar a la derivada e integral como funciones inversas.
.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: José Luis Abreu León y Leticia Montserrat Vargas Rocha |
 |
 |
Valor promedio de una función
Unidad didáctica - Proyecto Un_100
En esta unidad se presenta el Teorema del Valor Medio para integrales y en consecuencia el concepto de valor medio o promedio de una función. Como objetivos específicos se plantean:
• Conocer el Teorema del Valor Medio integral y comprobarlo en diversos casos prácticos.
• Dar una interpretación geométrica. • Calcular el valor medio de una función y el punto en el que se alcanza. Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Mª José García Cebrián |
 |
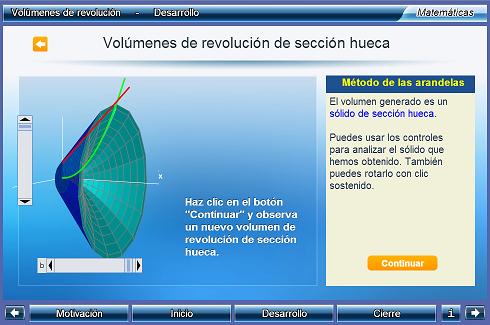 |
Volúmenes de revolución
Unidad didáctica - Proyecto Un_100
Una de las aplicaciones de la integral definida es el cálculo del volumen de un sólido de revolución, que se obtiene al rotar una región del plano alrededor de una recta de ese mismo plano. En esta unidad se busca el logro del siguiente objetivo:
''Calcular volúmenes de revolución generados por el giro alrededor del eje OX de la región limitada por una o dos funciones"
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Juan Guillermo Rivera Berrío |
 |
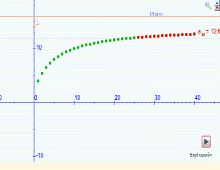 |
Sucesiones
Miscelánea
Escena interactiva en la cual, dada una sucesión, se establece un intervalo de estudio donde se observa la convergencia, acotación y monotonía. Se presentan dos gráficas, una de los términos de la sucesión en la recta real y otra sobre el plano. Ambas en el intervalo de estudio definido.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
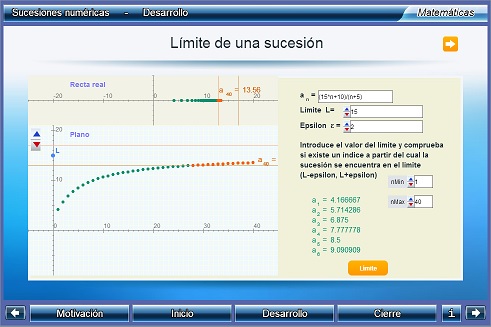 |
Sucesiones numéricas
Unidad didáctica - Proyecto Un_100
Se presentan algunos conceptos relacionados con las sucesiones, y dos tipos especiales de ellas: las aritméticas y las geométricas. Asimismo, se estudia el problema del límite de una sucesión, mostrando gráficamente el significado de convergencia a un número real, y de divergencia a infinito.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz |
 |
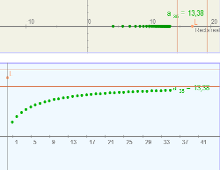 |
Límite de una sucesión
Miscelánea
A partir del término general de una sucesión, an, se analiza si la sucesión es convergente a un valor L. En el caso de que para cualquier valor de epsilon, todos los términos de la sucesión salvo un número finito, se encuentren en el intervalo (L-epsilon,L+epsilon) se concluirá que L es el límite.
OBJETIVOS
1. Interpretar gráficamente la convergencia de una sucesión
2. Representar en la recta real y en el plano los términos de una sucesión.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz |
 |
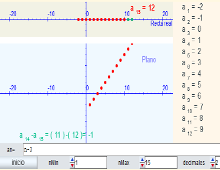 |
Monotonía de una sucesión
Miscelánea
Escena interactiva donde dada una sucesión y un intervalo donde se representan los términos, se observa si la sucesión es monótona. Se visualizan dos gráficas, una en la que se representan los términos de la sucesión en la recta real y en la otra, los mismos términos sobre el plano
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
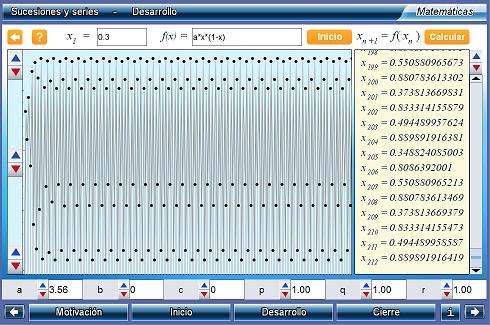 |
Sucesiones y series
Unidad didáctica - Proyecto Un_100
El objetivo de esta unidad es introducir al alumno al concepto de sucesión. Para ello, se proporciona una ecuación inicial, cuyos parámetros pueden modificarse. El alumno puede editar la ecuación misma para probar ecuaciones de su elección. La sucesión se calcula paso a paso para observar cómo cambia respecto al parámetro n. Es posible observar, en caso de que la haya, que la sucesión tiene una cota que no es rebasada, y ésta es gráficamente representada por una recta para introducir el concepto de asíntota. Lo mismo se hace con sucesiones generadas mediante la aplicación recursiva de una función y las sucesiones correspondientes a una serie.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: José Luis Abreu León y Alejandro Radillo Díaz |
 |
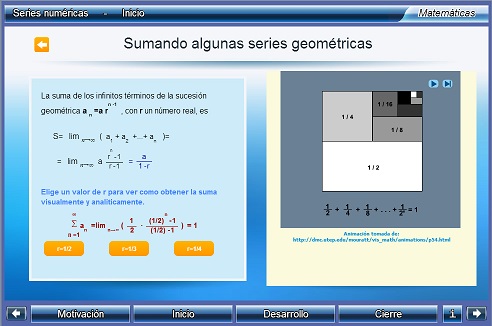 |
Series
Unidad didáctica - Proyecto Un_100
Los objetivos de la unidad son los siguientes:
- introducir el concepto de convergencia de una serie
- analizar la convergencia de algunas series notables como son las aritméticas y las geométricas .
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz |
 |
 |
Series de potencias. Polinomios de Taylor
Miscelánea
Escena interactiva donde se practica con el concepto de serie de potencias en torno a un punto, así como el entorno de dicho punto en el que la serie converge. A continuación se puede practicar con el polinomio de Taylor de una función f(x) y estudiar también para qué valores de x dicho polinomio converge a f(x).
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
 |
Polinomios de Taylor
Miscelánea
Escena interactiva que muestra el polinommio de Taylor hasta el grado 4 de una función.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
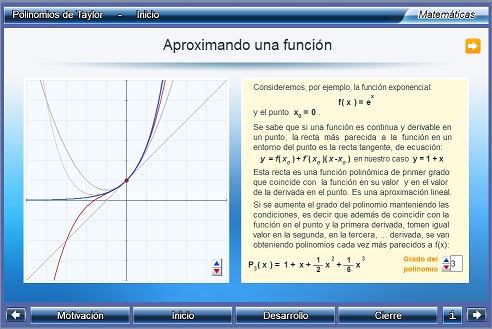 |
Polinomios de Taylor
Unidad didáctica - Proyecto Un_100
El objetivo de esta unidad es conocer y aplicar el polinomio de Taylor para la aproximación local de funciones y medir el error de esa aproximación; observando la incidencia que tiene en esta medida el grado del polinomio utilizado y la cercanía al punto en el que se hace el desarrollo.
.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Mª José García Cebrián |
 |
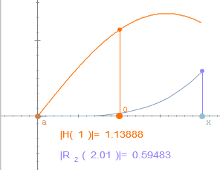 |
Polinomios de Taylor. Resto de Lagrange
Miscelánea
Escena interactiva donde se analiza la acotación del resto del polinomio de Taylor de una función f(x) en un punto.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
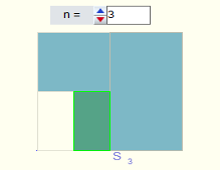 |
Series. Suma parcial enésima
Miscelánea
Escena interactiva que visualiza el concepto de convergencia de una serie numérica real considerando la convergencia de la sucesión de sus sumas parciales.
Para practicar se pueden considerar o bien dos tipos de series notables (geométricas o armónicas) o bien cualquier otra cuyo término general se pueda escribir con un máximo de dos parámetros.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz |
 |
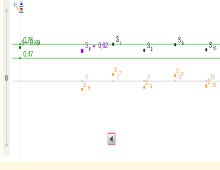 |
Series Alternadas. Suma aproximada
Miscelánea
Escena interactiva que analiza la suma aproximada de una serie alternada convergente por Leibniz. Al sustituir el valor S de la suma de los términos de una sucesión por la suma de sus n primeros términos, Sn, se comete un error que es, en valor absoluto, inferior al valor absoluto del término n+1 de la sucesión.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
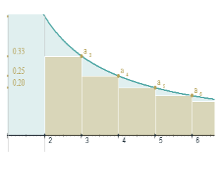 |
Resto enésimo. Criterio de la integral
Miscelánea
Escena interactiva en la que se practica la acotación del resto mediante el criterio integral de series geométricas, armónicas o cualquiera introducida por el usuario. También se muestra la representación gráfica de dicha acotación.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Elena E. Álvarez Sáiz
|
 |
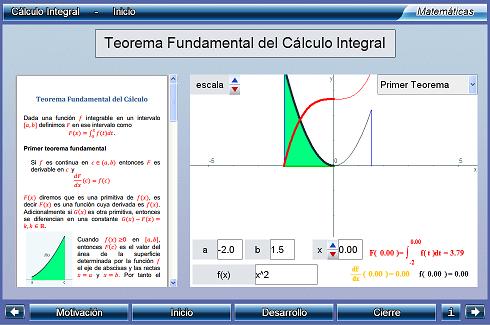 |
Cálculo integral
Unidad didáctica - Proyecto Un_100
La determinación de la recta tangente a una curva y el cálculo de áreas son dos problemas que han ido resolviéndose históricamente por caminos diferentes y, a priori, parecen no tener relación. Pero el Cálculo Diferencial permitió mostrar que, ambos, no son más que dos caras de la misma moneda. Adicionalmente, la autoría de éste cálculo fue muy disputada entre Newton y Leibniz y ello dio base a establecer que la misma queda asociada a la fecha de publicación. Newton y Leibniz fueron dos genios, mal avenidos, pero ciertamente ambos llegaron a ver más no sólo por ir a hombros de gigantes, sino porque ambos supieron mirar muy lejos. En esta unidad se:
a) Formula el Teorema fundamental del Calculo Integral que relaciona a la funcón área con la derivación
b) Se enunciar la Regla de Barrow que permite el cálculo de la integral definida en base a las primitivas de una función y consecuentemten establece la necesidad de calcular dichas primitivas.
c) Aprender a calcular primitivas por diferentes métodos.
d) Aplicación al cálculo de áreas de trapecios mixtilíneos y área encerrada entre dos curvas Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: José R. Galo Sánchez |
 |
 |
Cálculo integral
Libro digital interactivo - iCartesiLibri
Siguiendo una estrategia similar a la seguida por el autor del conocido libro “El mundo de Sofía”, Paco entabla una conversación con su profesor que le permite adentrarse y explorar la integrales bajo un punto de vista procedimental y otro de aplicación al cálculo.
.
Área: Ciencias básicas - Cálculo
Nivel: Ingeniería y Tecnología
Autor: Varios autores. Editor: Juan Guillermo Rivera Berrío
|
 |
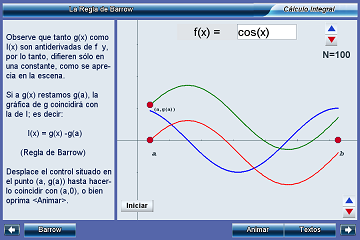 |
La regla de Barrow
Unidad didáctica
El objetivo de esta unidad es arribar de manera visual al teorema de Barrow para encontrar la integral definida desde a hasta x.
.
Área: Ciencias básicas - Cálculo
Nivel:Bachillerato, Ingeniería y Tecnología
Autor: José Luis Abreu León.
|
 |
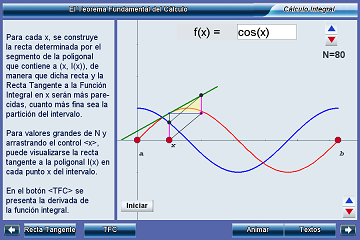 |
El teorema fundamental del cálculo
Unidad didáctica
El objetivo de esta unidad es la visualización dinámica del teorema fundamental del cálculo.
.
Área: Ciencias básicas - Cálculo
Nivel:Bachillerato, Ingeniería y Tecnología
Autor: José Luis Abreu León.
|
 |