El alumnado como productor de cultura digital con el modelo BYOD
Escrito por José Antonio Salgueiro GonzálezCon motivo de la Jornada 50yTICo, celebrada en septiembre en el hiperaula de la Facultad de Educación de la Universidad Complutense de Madrid, y que difundimos desde nuestro portal con "Una crónica de la Jornada 50yTICo", se generó un importante movimiento de información desde el claustro virtual en Twitter con el hashtag #50yTICo, y tuve la ocasión de acceder al artículo titulado "Sobre TIC, Web 2.0 y cultura digital en educación" publicado en 2017 por José Luis Cabello, a quien tengo la fortuna de conocer personalmente y aprovecho para enviar un cordial saludo. Pues bien, este artículo me ha motivado para reflexionar y compartir experiencias sobre la creación de contenidos por parte del alumnado, uno de los aspectos adecuados para el desarrollo de su competencia digital, y todo ello integrado desde la materia de mi especialidad. Aunque quizás no dispongamos de un plan específico de integración de la competencia digital en matemáticas, entre los contenidos del bloque uno, denominado "Procesos, métodos y actitudes en Matemáticas", tanto en la ESO como el Bachillerato, se contempla la utilización de medios tecnológicos en el proceso de aprendizaje para la elaboración de informes y documentos sobre los procesos llevados a cabo y los resultados y conclusiones obtenidos. A su vez, en los criterios de evaluación para este bloque aparece utilizar las tecnologías de la información y la comunicación de modo habitual en el proceso de aprendizaje, buscando, analizando y seleccionando información relevante en Internet o en otras fuentes, elaborando documentos propios, haciendo exposiciones y argumentaciones de los mismos y compartiendo éstos en entornos apropiados para facilitar la interacción. Pero más específicos aún son los estándares de aprendizaje evaluables, donde se recoge:
- 12.1. Elabora documentos digitales propios (texto, presentación, imagen, video, sonido,…), como resultado del proceso de búsqueda, análisis y selección de información relevante, con la herramienta tecnológica adecuada, y los comparte para su discusión o difusión.
Ahora bien, ¿cómo idear estrategias didácticas y diseñar actividades de aula para aplicar estos criterios de evaluación junto a sus correspondientes estándares de aprendizaje? Peor aún, ¿cómo hacerlo en el aula de un centro que no dispone de equipamiento? Parece ser que a la primera pregunta debemos responder con creatividad e imaginación docentes y compartiendo y divulgando experiencias. Sin embargo, para la segunda se propone en el artículo mencionado el denominado BYOD, que se refiere a Bring Your Own Device, es decir, que cada alumno o alumna traiga su propio dispositivo al aula, lo que viene a ser el Programa Escuela 2.0 pero con las familias encargadas de sufragar los dispositivos. Así que todo ello viene a ratificar mis manifestaciones en algún que otro tuit cuando difundo el lema de que "No existe otro camino que el de la Escuela 2.0".
Pero no creas que aquí terminan todos los obstáculos para cumplir con lo que se te exige como docente, porque todavía puede ocurrir que tu centro, en el ámbito de su autonomía, decida prohibir el uso de dispositivos móviles amparándose en que uno o dos alumnos han hecho un mal uso de los mismos. Por cierto, al momento de redactar este artículo, cierta comunidad autónoma anuncia que "impedirá de forma explícita la utilización de teléfonos y otros dispositivos electrónicos en los periodos lectivos, «salvo en aquellos casos que esté expresamente previsto en el proyecto educativo y siempre con fines didácticos»". Me pregunto si se llegarán a prohibir algún día el uso del compás, la tijera o el cúter en el aula por tratarse de armas blancas.
Recomiendo la difusión del "Decálogo del buen uso de la tecnología móvil en el aula", elaborado por el grupo de trabajo sobre el buen uso de los dispositivos móviles en el aula, en el marco de la Jornada 50yTICo.
Para finalizar esta pequeña reflexión, ¿cómo podemos desarrollar las competencias clave sin equipamiento de aula y sin BYOD?
Comparto aquí una propuesta basada en varios proyectos que vengo desarrollando desde hace algunos años, que son perfectamente extrapolables a otras materias y especialidades, donde el alumnado utiliza sus propios dispositivos móviles fuera del aula.
| DESARROLLO DE LA COMUNICACIÓN AUDIOVISUAL |
Se trata de un proyecto que llevo a cabo con el alumnado de 4º ESO y cuyos orígenes se encuentran en el artículo del mimo nombre, es decir, "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes", habiendo publicado hasta el momento varias producciones con distinta temática en cada edición, así tenemos "Matemáticas para todos con Descartes", dedicado a fracciones algebraicas, "Los alumnos pueden aprender divirtiéndose y generando contenido inédito", dedicado a ecuaciones y sistemas lineales, "Aprendemos a resolver problemas con Descartes y Wiris", dedicado a la búsqueda de un modelo matemático para la resolución de un problema o el compartido en este artículo, dedicado a la maqueta como instrumento para entender la semejanza de figuras.
| LA RADIO FICCIÓN EN EL AULA |
Se trata de un proyecto que llevo a cabo con el alumnado de 3º ESO y cuyos orígenes se encuentran en el artículo del mimo nombre, es decir, "La radio ficción en el aula de Matemáticas", habiendo publicado hasta el momento varias producciones como "Sophie Germain: la primera mujer en acceder a la Academia de Ciencias de París", "Ada Lovelace, la mujer en la ciencia y el techo de cristal", "Évariste Galois visto e interpretado por alumnos de 3º ESO", "Alumnas de 3º ESO entrevistan a Mary Somerville" o la entrevista a Leonardo de Pisa, conocido como Fibonacci, compartida en este artículo.
| EL ALUMNADO COMO GENERADOR DE CONTENIDO CON DESCARTES JS |
Se trata de un proyecto que llevo a cabo con el alumnado de 1º Bachillerato y cuyos orígenes se encuentran en el artículo del mimo nombre, es decir, "El alumnado como generador de contenido multimedia con Descartes JS", que cuenta con otra experiencia de año distinto titulada "¿Sabes que tu alumnado puede generar fácilmente contenido multimedia con Descartes JS?" y que ampliamos en este artículo con producciones del curso 2018/2019.
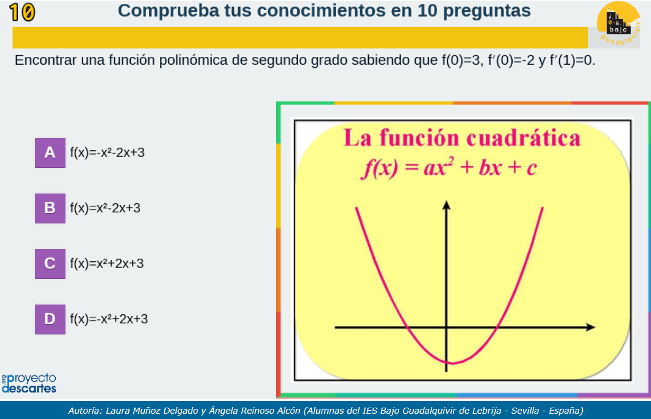
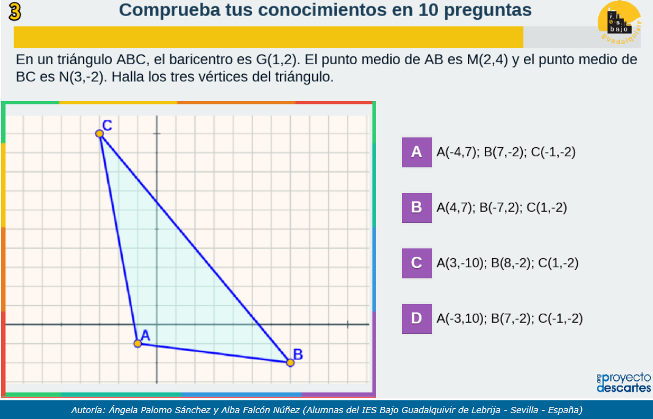
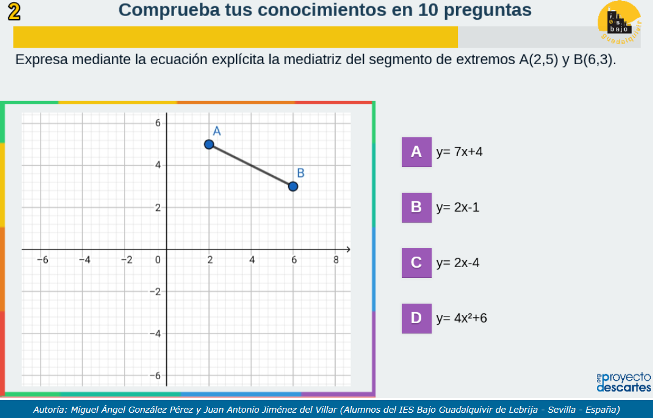
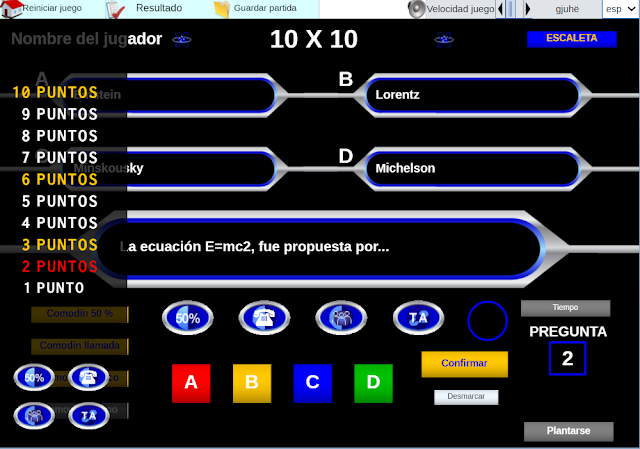
Autoevaluación - 9, generada por el equipo Émilie du Châtelet
Autoevaluación - 10, generada por el equipo Sofia Kovalévskaya
Autoevaluación - 11, generada por el equipo Carl Friedrich Gauss
Quiero felicitar a todos mis alumnos y alumnas que, año tras año, son capaces de superar los retos que les planteo, con su creatividad e imaginación, utilizando sus propias herramientas tecnológicas en sus domicilios y sin la intervención del profesor, mostrando sus capacidades ocultas y demostrando que son plenamente competentes para trabajar de forma colaborativa y en la distancia. Asimismo, mi gratitud a sus familias por autorizar la publicación y difusión de estas producciones digitales, conscientes de que repercuten notablemente en la formación de sus hijos e hijas.
Red Educativa Digital Descartes os desea Feliz Navidad y Próspero Año 2020.
Escena creada con DescartesJS por Juan Guillermo Rivera Berrío desde RED Descartes Colombia y la Institución Universitaria Pascual Bravo
En este artículo presentamos la unidad “Permutaciones y Combinaciones” del proyecto Un-100 perteneciente a la Red Educativa Digital Descartes.
El proyecto Un_100 comprende unidades didácticas del nivel universitario en la áreas de Matemáticas y de Física. Algunas unidades también son adecuadas para los últimos cursos de la ESO y para el bachillerato.
Todas las unidades tienen un mismo esquema o plantilla común con cuatro apartados: motivación, inicio, desarrollo y cierre. En la unidad que presentamos se proponen actividades de introducción y resolución de problemas aplicando las reglas de permutaciones y combinaciones.
Las actividades propuestas en cada apartado son las siguientes:
- Motivación: Se exponen dos vídeos de introducción al tema.
- Inicio: Tres escenas con las definiciones y ejemplos de factorial de un número, permutaciones y combinaciones.
- Desarrollo: Tres escenas con problemas de aplicación de los conceptos introducidos. En cada actividad el alumnado debe calcular número de permutaciones o combinaciones con distintos subconjuntos y diferenciar en cada caso. En todas las actividades el estudiante puede comprobar si su respuesta es la correcta.
- Cierre: También consta de tres escenas. En primer lugar un resumen de las definiciones y fórmulas, una segunda escena con ejercicios de consolidación y por último una autoevaluación.
El Proyecto AJDA en la Red Descartes
Escrito por Jesús Manuel Muñoz Calle- Poder utilizar los servidores de Descartes, así como de otros recursos informáticos.
- Ofrecer la difusión de gran cantidad de recursos educativos de forma gratuita y accesible a nivel nacional e internacional.
- Mejorar y actualizar continuamente la aplicación Descartes, su editor y materiales relacionados
- Disponer de asesoramiento técnico sobre el aplicativo de Descartes y la posibilidad de realizar sugerencias para la integración de nuevas funcionalidades en el mismo. Cabe destacar lo mucho que ha mejorado y su continuo desarrollo.
- Registrar oficialmente la publicaciones que se realizan.
- Disponer del blog del Descartes para realizar publicaciones mensuales de artículos sobre AJDA.
- Contar con la ayuda y colaboración de los compañeros de Descartes y de su Junta Directiva.
- Ofrecer formación técnica y didáctica a sus socios a través de distintas vías.
iCartesiLibri. Matemáticas básicas
Escrito por Montserrat Gelis BoschEn este artículo presentamos matemáticas básicas, un libro digital que pertenece al proyecto iCartesiLibri y que presenta una recopilación de contenidos y ejercicios de aritmética y álgebra.
El libro contiene actividades de repaso de conceptos elementales:
- Definición, clasificación y cálculo con los números reales
- Potenciación
- Radicación
- Expresiones algebraicas
- Factorización
- Fracciones algebraicas
En las páginas del libro digital encontramos, además de la introducción y definición de los diferentes conceptos, múltiples ejemplos y actividades interactivas que permiten al estudiante interactuar con las escenas, favoreciendo y potenciando el autoaprendizaje.
Para trabajar en el aula se puede insertar directamente el enlace a la unidad desde cualquier espacio web o mediante el código para embeber o abrir en ventana emergente. Dichos códigos los podemos encontrar en el apartado correspondiente de la página de la red.
En el siguiente vídeo se muestran algunas de las actividades que contiene esta unidad y las diferentes formas de insertar el libro en un espacio web.
Dos escenas del décimo aniversario del proyecto Descartes
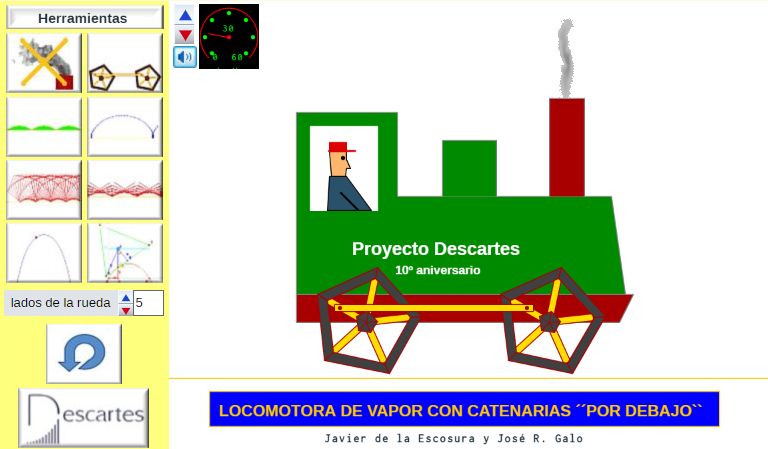
Escrito por José R. Galo SánchezEn junio de 2008 el proyecto Descartes cumplió su décimo aniversario y nuestro compañero Javier de la Escosura nos sorprendió con una bonita, graciosa e interesante escena que tituló "Locomotora de vapor con «Catenarias por debajo»". Una locomotora de ruedas cuadradas que, obviamente, para poder circular requiere de una vía especial cuyo perfil es el de la función denominada catenaria. Y la rotuló con el texto "Proyecto Descartes 10º Aniversario" como regalo al grupo cartesiano en dicha celebración. Un bonito juguete para todos los cartesianos en su niñez como proyecto.
Esa escena fue generalizada para poder seleccionar una rueda poligonal con el número de lados que deseara el usuario e incluyendo algunas utilidades adicionales en las que, usando el rastro de las ruedas, se simulaba la construcción de la vía necesaria para su circulación y en ella se incluyó sonido ambiental. Dos juguetes para gozo y disfrute de entusiasmados niños.
Pero en 2012, cuando surgieron los bloqueos de los plugins de Java que nos complicó durante cierto tiempo la gestión de la herramienta Descartes hasta su traslación a la actual DescartesJS, ambas escenas quedaron guardadas en nuestra antigua web, pero sin adaptar al nuevo intérprete. Se reprodujo una situación que suele ser habitual en la vida humana en la que de niños somos incapaces de separarnos de nuestros juguetes y en la adolescencia estos quedan olvidados, e incluso arrumbados, en un cajón. Es en la madurez, o incluso la cercanía de la senectud, la que hace recordar y recuperar elementos que provocan el renacimiento de sensaciones, sonrisas y alegrías. El proyecto Descartes tiene ahora veintiún años, una mayoría de edad en la escala humana y una juventud incipiente, pero en la escala de rápidos avances y cambios tecnológicos esa edad se corresponde con la madurez antes citada y, por tanto, era necesario, imprescindible, rescatar esos dos juguetes. Y aquí están de nuevo disponibles para todos, para disfrute de cartesianos expertos (condescendiente eufemismo de mayores) y cartesianos noveles.
Pulsa sobre la imagen para abrir la escena
Pulsa sobre la imagen para abrir la escena
Y puestos a recordar os enlazamos una versión actualizada del artículo divulgador de ese décimo aniversario (únicamente se ha vuelto a enlazar adecuadamente todos los vínculos que habían quedado desfasados). Aquellos eran años de ilusión docente e innovadora del grupo cartesiano que en aquel momento eran canalizados por el Ministerio de Educación español y ahora son años de ilusión incrementada como la organización no gubernamental "Red Educativa Digital Descartes" que conformamos y que fundamos en junio de 2013.
Artículo publicado en la revista Epsilon
Escrito por Ángel Cabezudo BuenoEn el número 102 de la revista Epsilon (ISSN: 2340-714X) de la Sociedad Andaluza de Educación Matemática Thales se ha publicado el artículo titulado "Partición prismática de paralelepípedos en seis pirámides triangulares equivalentes" cuyo autor es nuestro socio José R. Galo Sánchez. Un trabajo de investigación, que como se refleja en la filiación de la autoría, ha sido desarrollado dentro de nuestra RED Descartes.
Este trabajo generaliza el publicado en 2018 con el título "Partición prismática de un cubo en seis pirámides triangulares equivalentes" y en él, como se refleja en el resumen:
"Se analiza en detalle la descomposición de los diferentes tipos de paralelepípedos en pirámides cuadriláteras y en pirámides triangulares. Se obtienen de manera constructiva las particiones con cardinal mínimo y se profundiza en aquellas que, sin tener cardinal mínimo, están formadas por seis pirámides que forman dos prismas. Se cuantifican y detallan todas las particiones posibles y se proporcionan enlaces a recursos interactivos que permiten verlas digitalmente y, a su vez, también obtener los desarrollos planos con los que abordar su reproducción real o tangible y su manipulación. Para cualquier paralelepípedo que defina el interesado se obtiene un entretenido puzle, no siempre fácil de componer."
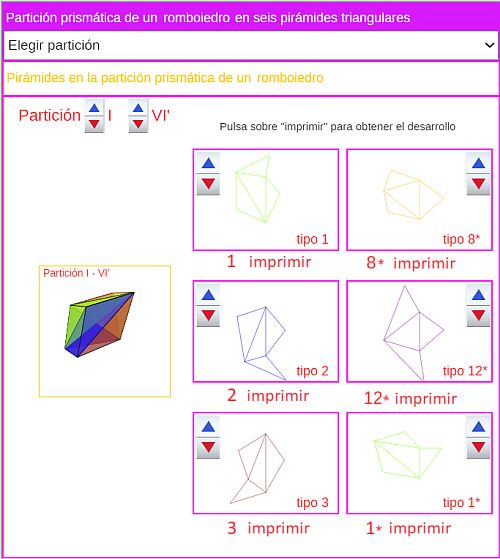
Por ejemplo, en la siguiente escena se han englobado todas las posibilidades al permitir al usuario seleccionar el tipo de paralelepípedo que quiera, indicar las dimensiones que desee, elegir una partición de todas las posibles y, procediendo a imprimir los desarrollos planos de las pirámides que la componen, pasar a construir, como un puzle, un modelo tangible del paralelepípedo considerado. Para ello, en la escena, se cuenta con un menú con las siguientes opciones:
- Selecciona el paralelepípedo (Cubo, Ortoedro, Romboedro con corte por la diagonal menor o la mayor y Romboiedro).
- Ver el desarrollo plano de las diferentes pirámides que pueden aparecer en la partición del paralelepípedo.
- Elegir la partición que se desee construir, reflejándose los desarrollos planos de las seis pirámides que intervienen en la misma, pudiendo proceder a la impresión de cada uno de ellos.
Pulsa sobre la imagen para abrir la escena
Os incluimos a continuación dicho artículo y os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales. También a que, usando los recursos interactivos ahí enlazados y disponibles en nuestra web, construyáis particiones de diferentes paralelepípedos y en el aula abordéis su reconstrucción y propiedades.
Finalmente destaquemos que el autor, en las conclusiones del estudio, nos señala que el germen de este análisis fue la observación de una escena desarrollada en el año 2001 por nuestra colega Ángela Núñez Castaín, entrañable y querida pionera del proyecto Descartes. En concreto, en esas conclusiones se refleja que el exhaustivo estudio realizado:
"Comprende una amplia casuística que surgió a raíz de la adaptación a DescartesJS de una escena en la que se observaba una partición prismática de un cubo (Núñez Castaín, A., 2001) y en cada uno de los prismas, en los que quedaba dividido, aparecían diferentes tipos de pirámides equivalentes entre sí. Al abordar el análisis de la situación se comprobó que las referencias a las particiones de un cubo en pirámides quedaban planteadas de manera deslavazada o inconexa, mostrando sólo aquellos casos particulares en los que se encuentra mayor regularidad, pero no desde un punto de vista global e integrador. Eso fue el objetivo primario de estudio realizado en un artículo anterior (Galo-Sánchez J.R., 2018) y el objetivo secundario su generalización a los paralepípedos que es lo que aquí ha quedado realizado. La extensión a hexaedros convexos de caras cuadriláteras {4,4,4,4,4,4}, como poliedro no regular que puede considerarse similar al cubo, también ha sido realizada por el autor e implica algunas particularidades adicionales interesantes que serán objeto de una publicación ulterior."
Ese último análisis ha sido descrito por el autor en la página 104 y siguientes del artículo interactivo "Partición de hexaedros convexos de caras cuadriláteras en pirámides" que está publicado en nuestro servidor dentro del proyecto de libros interactivos iCartesiLibri.
Descartes en moodle. Creando un cuestionario
Escrito por Montserrat Gelis BoschSiguiendo con la serie de vídeos Descartes en moodle vamos a mostrar, en este caso, cómo insertar una Unidad Descartes en un curso moodle y completando la actividad con un cuestionario de moodle.
La unidad de la RED seleccionada es Poliedros del subproyecto Unidades Didácticas.
En moodle vamos a insertar un enlace a esta unidad mediante el código para abrir en ventana emergente.
En la web Descartes podemos conseguir el código para embeber o abrir en ventana emergente de la mayoría de las unidades pero, en caso de no hallar la unidad o escena que buscamos, se puede modificar el siguiente código con las direcciones que corresponda:
<a href= "dirección web" target="_blank" onclick="window.open(this.href, this.target, 'width=1024,height=920,top=30,left=100,toolbar=0,menubar=0,scrollbars=1,resizable=1,location=0,status=0'); return false;">
<img src= "dirección de una imagen" alt="texto alternativo" style="display: block; margin-left: auto; margin-right: auto;"></a>
Se completa la actividad con la tarea cuestionario de moodle. Las múltiples posibilidades de configuración de un cuestionario de moodle (tipos de preguntas, número de intentos, métodos de calificación…) lo convierten en una herramienta muy útil de autoevaluación y seguimiento del progreso del estudiante, tanto para el alumnado como para el profesorado.
A modo de ejemplo se crean dos tipos de preguntas, una pregunta anidada (cloze) y otra de emparejamiento.
Una crónica de la Jornada 50yTICo
Escrito por José Antonio Salgueiro GonzálezEl sábado 21 de septiembre se celebró, en la Facultad de Educación de la Universidad Complutense de Madrid, la Jornada 50yTICo, con la participación de docentes de todas las etapas educativas, especialidades y comunidades autónomas, con el denominador común de contar con gran experiencia profesional y ser pioneros y vanguardistas en la incorporación generalizada de las TIC a la práctica docente, con el objetivo fundamental de "reflexionar lo que supuso la llegada de las TIC a las aulas y al denominado “claustro virtual”, estudiar y compartir cómo se ve la situación actual y diseñar algunas líneas de recomendaciones para el futuro", aportando toda la experiencia adquirida para "avanzar hacia una educación de calidad, inclusiva y del siglo XXI".
Tras el acto inaugural por parte de Domingo Méndez, en nombre de la organización, fuimos objeto de un cálido recibimiento por parte de Santiago Ortigosa, profesor titular del Departamento de Estudios Educativos de esta facultad y Coordinador del Campus Virtual, en el fabuloso espacio conocido como Hiperaula, donde se formarán los futuros maestros fomentando la codocencia, con una organización, dimensiones, mobiliario y equipamiento completamente diferentes a las tradicionales. Salvando la edad del alumnado a la que se destina, me recuerda al Aula del Futuro que tuve la oportunidad de conocer en las instalaciones de INTEF con motivo de las III Jornadas EDIA+EXE, desarrolladas en el mes de mayo.

Pudimos oir las sabias reflexiones de la Gran Mercedes allende los mares, que no pudo asistir por las situaciones derivadas de "Arrugas apreciadas", y enviamos un fuerte abrazo a nuestro compañero y amigo Juanma Díaz, a quien también echamos de menos, al igual que otras tantas personas que tanto han aportado y aportan a la Escuela.
En primer lugar, intervino Toni Solano, a quien no veía desde el II Encuentro de Experiencias de Escuela 2.0, hacía ya una década, pero me encantó poder abrazarlo después de tanto tiempo y disfrutar con su "RememberWare: gamifica tus recuerdos".
Seguidamente, agradezco a la organización que me ofreciera esta oportunidad para presentar, de forma desenfadada, una secuencia de imágenes y viñetas tomadas del portal de la Red de Buenas PrácTICas 2.0 para reflexionar sobre gran parte del período de la Escuela 2.0, y que denominamos "La revolución de la Escuela".
Se organizaron grupos de trabajo compuestos por cinco o seis personas para reflexionar y recopilar, en base a nuestras experiencias, propuestas que nos permitan elaborar un manifiesto o declaración "por la implementación de las TIC en los procesos de enseñanza y aprendizaje que nos lleve a un cambio metodológico real y en todos los ámbitos".
- Pizarras electrónicas / Ordenadores portátiles en el aula, moderado por Pere Marqués, a quien conocí en la VI Escuela de Verano de Almagro.
- Teléfonos móviles / Tablets, moderado por Olga Catasús, con quien coincidí el año pasado en el curso de verano "Con REAs y a lo loco", organizado por INTEF-CeDeC y la UIMP en Valencia.
- Sala de ordenadores / Coordinador TIC, moderado por Salomé Recio, a quien no veía desde el Encuentro de Cine y Educación en Madrid.
- Blogs / Metodologías con TIC, moderado por Paco Ruiz, con quien no coincidía desde el II Encuentro de Experiencias de Escuela 2.0 y me encantó volver a compartir algunos momentos.
- Formación / Encuentros / Eventos / Premios / Claustros TIC / Redes, moderado por Puerto Blázquez, a quien tuve la oportunidad de conocer.
Recibimos la visita de Jorge Cujó Arenas, Vicedecano de Asuntos Económicos e Infraestructuras de la Facultad de Educación, quien nos dió la bienvenida y ofreció las instalaciones y recursos de la institución para lo que necesitáramos, mostrándose además orgulloso de que docentes de tanta experiencia se congregaran en la Facultad de Educación.

El epílogo, de gran calidad y con grandes dosis de humor, estuvo a cargo de José Luis Sánchez y José Antonio Fraga, a quienes tuve el placer de conocer personalmente y que nos sorprendieron, además, con una actuación de magia. Comparto el vídeo, aunque podemos oirlo sin ver a estos grandes artistas.
En la siguiente imagen podemos ver un instante de "Ni contigo ni sin TIC", con José Luis Sánchez y José Antonio Fraga.

La lectura, puesta en común y conclusiones de los diferentes grupos de trabajo estuvo a cargo de Salvador Barrientos, a quien tuve la fortuna de conocer en esta jornada, y pueden oirse en el último vídeo. No obstante, la declaración final se publicará en el blog 50yTICo y puedes seguir la información en Twitter desde el hashtag #50yTICo.
Para mí ha sido un honor participar y compartir en esta apasionante jornada, reencontrarme con compañeros a los que hacía muchos años que no veía físicamente y conocer personalmente a todos los asistentes a la misma, así como representar y dar voz a RED Descartes, sin olvidar que sus miembros abrieron el camino oficial para la creación de la Red de Buenas PrácTICas 2.0.
¡Nos vemos en las II Jornadas 50yTICo!

Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)





 CONTACTO
CONTACTO
