DescartesJS
Nivel I
INTERACTIVO
Juan Guillermo Rivera Berrío
Institución Universitaria Pascual Bravo
Joel Espinosa Longi
Alejandro Radillo Díaz
Universidad Nacional Autónoma de México
Título de la obra:
DescartesJS - Nivel I
Autores:
Juan Guillermo Rivera Berrío
Joel Espinosa Longi
Alejandro Radillo Díaz
2ª edición – 2019
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Núcleo del libro interactivo: julio 2022
Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
ISBN: 978-958-56858-2-6
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto DescartesJS: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red, a excepción de algunos vídeos incluidos en el texto. Todos los objetos interactivos se han diseñado con el Editor DescartesJS.
Véase https://proyectodescartes.org/iCartesiLibri/descripcion.htm.
El contenido de este libro se basa en un curso de capacitación del editor DescartesJS para docentes que, por la dificultad de concertar un horario presencial, permite una opción autodidacta acompañada de material interactivo para una mayor comprensión de los temas tratados.
Retomando la introducción a la documentación de DescartesJS de Radillo, Abreu y Espinosa, podríamos coincidir en que este libro está destinado tanto a personas que no han usado DescartesJS como a personas que tienen cierta experiencia y desean mejorarla. En cada apartado del libro se proponen ejercicios y se incluyen ejemplos para que el lector pueda comprender paso a paso la funcionalidad de DescartesJS y su enorme potencial para crear objetos interactivos de aprendizaje. Esta es la primera parte de un curso piloto aplicado a un grupo de docentes, interesados en generar sus propios objetos interactivos con DescartesJS. En una segunda parte, se explorarán elementos de programación, que permitan generar escenas de mayor complejidad a las presentadas en esta primer parte. Es importante precisar que en este libro se incluye documentación tomada del texto de Radillo et al, en especial la introducción a cada capítulo.
Presentamos dos ejemplos, que esperamos sirvan como motivación a los lectores. El primer ejemplo es un objeto del proyecto Un_100 (haz clic sobre la siguiente imagen para explorarlo).
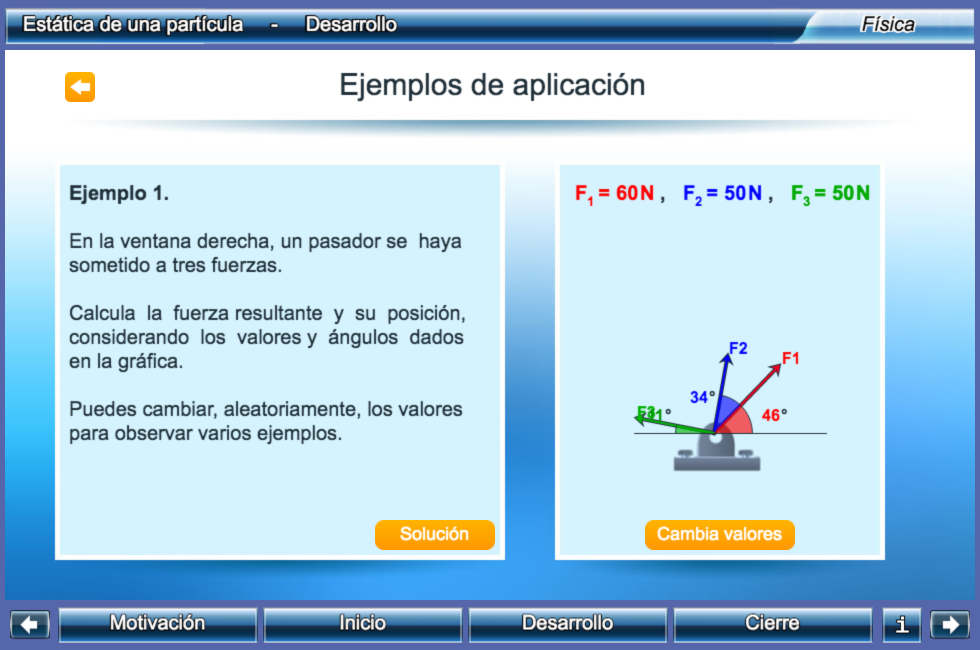
El segundo ejemplo es una escena interactiva diseñada para el libro digital interactivo de Física, volumen II, con el cual puedes interactuar en esta página o, si lo deseas, ampliarlo en una ventana emergente presionando el botón .
El editor consiste en un programa ejecutable (DescartesJS.exe en Windows, DescartesJS.app en macOS o DescartesJS.bin en Linux), el instalador puede descargarse desde: http://descartes.matem.unam.mx/, que se encuentra en constante mantenimiento incluyendo nuevas mejoras, de tal forma que es siempre una buena práctica reinstalarlo con cierta frecuencia. El programa del editor es una interfaz gráfica para el usuario mediante la cual podrá guardar archivos html con diversos tipos de interactivos. En la se muestra la ventana inicial del editor, el cual se puede buscar dentro de los programas en el ordenador, una vez que se haya instalado.
Puedes explorar el menú del editor o consultar la información presentada en la documentación de Radillo et al, sobre la cual no nos detendremos en este apartado, en tanto que a medida que avancemos podrás comprender mejor algunas opciones presentadas en el menú del editor.
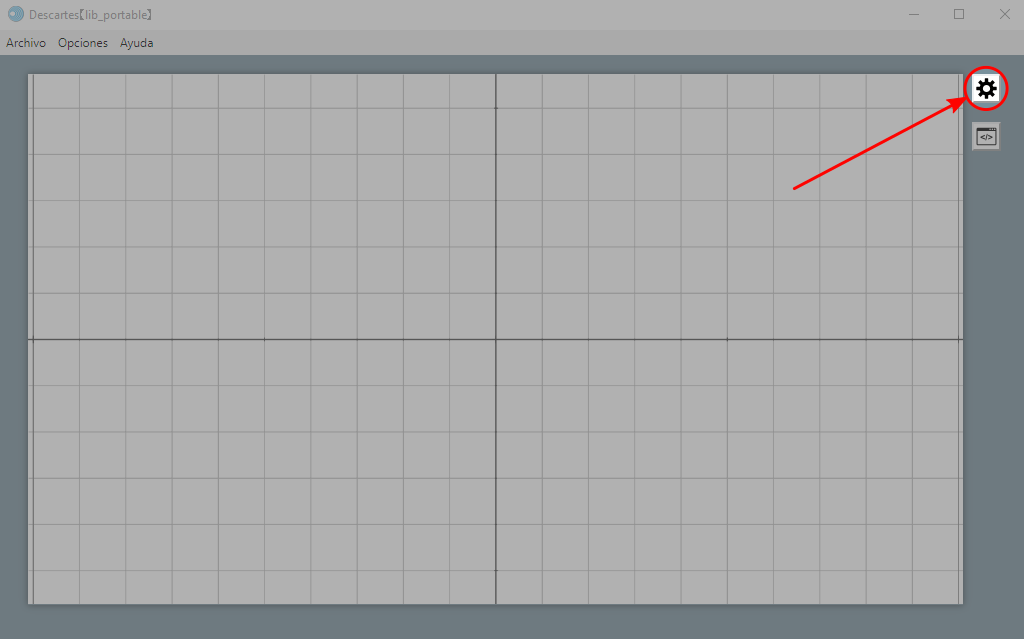
El editor de configuraciones es una nueva ventana desde donde se realiza la programación del recurso interactivo y se muestra al oprimir el botón con forma de engranaje, que se encuentra en el extremo derecho de la ventana principal del Editor. La muestra la ubicación de dicho botón.
El botón inferior con los corchetes muestra una pantalla en la que se puede editar directamente el código de la escena, que no usaremos en este nivel. En la se muestra la ventana del editor de configuraciones. Como se observa, contiene en su parte superior un menú de selectores esenciales para su uso.
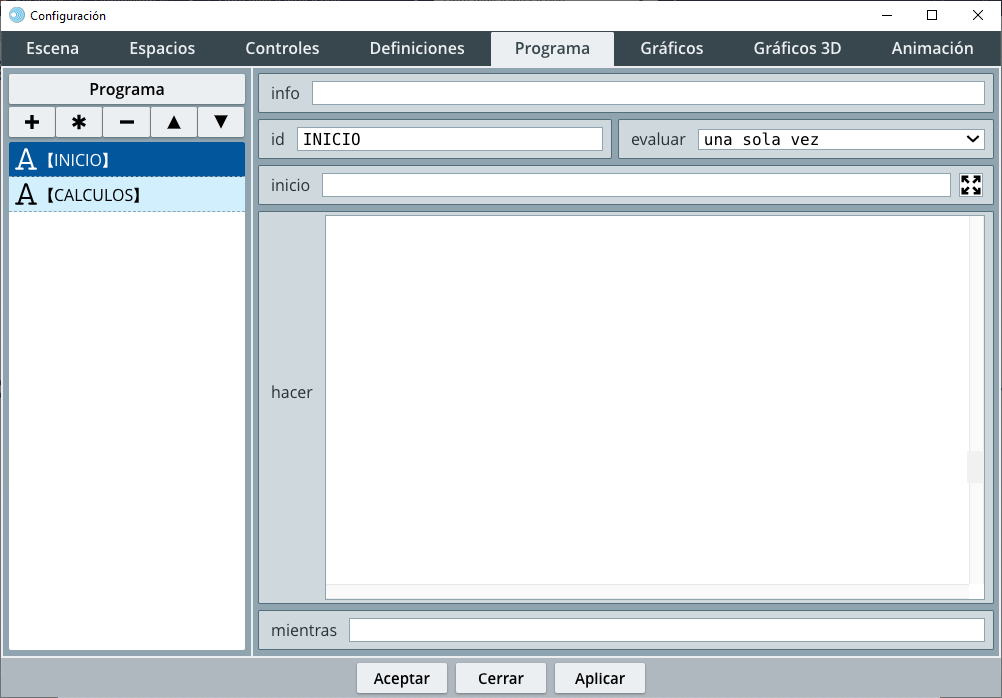
El contenido principal del editor de configuraciones consiste en siete selectores para editar diferentes partes del interactivo, que aumenta a ocho cuando se crea un espacio 3D. La comprensión de cada uno de ellos se hará a medida que avances en los siguientes capítulos; no obstante, de Radillo et al, transcribimos:
El selector Escena permite hacer cambios de la interfaz general de la escena con el usuario.
El selector Espacios se usa para añadir, duplicar, eliminar o editar las propiedades de los espacios existentes en un interactivo. Los espacios son áreas en las que se presenta material gráfico al usuario.
El selector Controles permite añadir, duplicar, eliminar o editar las propiedades de los controles que se encuentran en el interactivo. Dichos controles son aquellos elementos con los que el usuario puede interactuar directamente.
El selector Definiciones permite añadir, duplicar, eliminar o editar las propiedades de los elementos que componen la programación del interactivo. Esta parte contiene elementos dentro de los cuales se encuentra el código fuente dentro de un interactivo.
El selector Programa contiene los algoritmos y eventos. Al igual que las definiciones, éstos contienen parte del código que permite el funcionamiento del interactivo. En particular, se refiere a la preparación inicial del interactivo para que esté listo para usarse, pero también a instrucciones que se repiten siempre o dadas ciertas condiciones.
El selector Gráficos permite añadir, duplicar, eliminar o editar las propiedades de los gráficos mostrados en los espacios 2D.
El selector Gráficos 3D permite añadir, duplicar, eliminar o editar las propiedades de los gráficos mostrados en los espacios 3D.
El selector Animación permite editar las instrucciones y condiciones de una animación en caso de haberla.
Todos estos selectores los abordaremos con más detalle en los siguientes capítulos. Cabe mencionar que hay disponible una explicación o información emergente (tipo tooltips) para los diferentes elementos dentro de los selectores. Por ejemplo, el parámetro hacer mostrará su tooltip si se posa el ratón sobre el texto
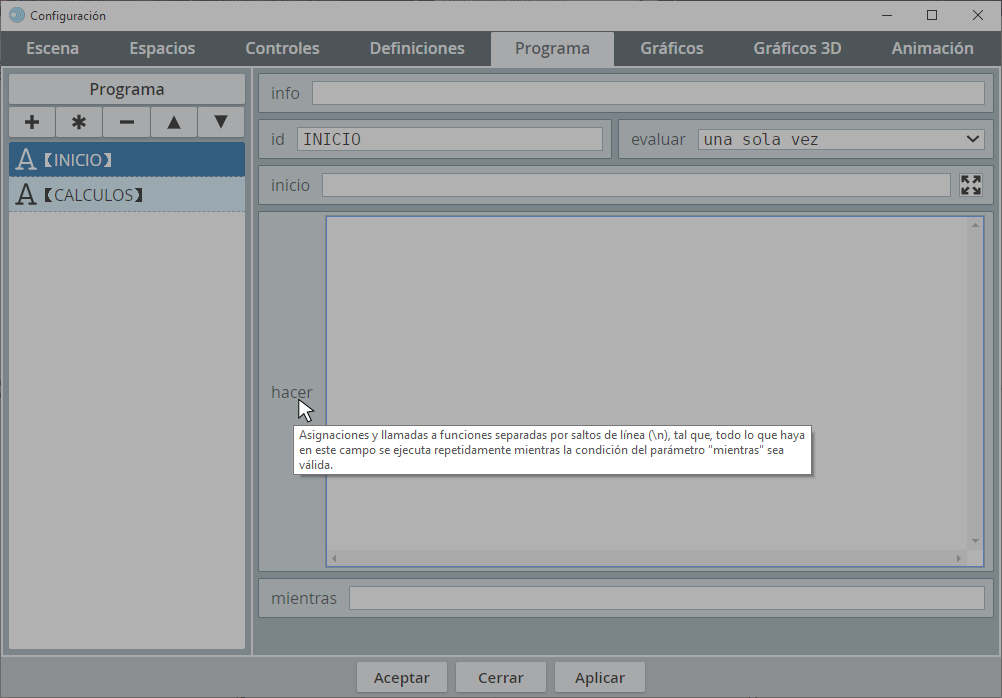
hacer.Al terminar este capítulo, habrás diseñado el siguiente objeto interactivo:
En el espacio bidimensional de la esquina superior izquierda, puedes mover el plano cartesiano con clic sostenido. Sobre el espacio tridimensional, puedes rotar el objeto con clic izquierdo sostenido, o cambiar su tamaño con clic derecho sostenido. En el espacio de la parte inferior, se muestra un vídeo de YouTube que puedes reproducir. El objeto interactivo no tiene ninguna intencionalidad didáctica, es sólo un ejemplo demostrativo de las propiedades de los espacios cartesianos.
Son tres los espacios que podemos usar con DescartesJS: $ℝ^2$ o bidimensional, $ℝ^3$ o tridimensional y los de tipo HTMLIframe que permiten incorporar cualquier tipo de página web.
Cuando ejecutas el Editor de DescartesJS, por defecto, siempre se muestra un espacio cartesiano bidimensional. Este espacio se identifica (en el selector Espacios) normalmente como E1. En la se pueden observar los controles para este espacio (debes activar el selector Espacios).
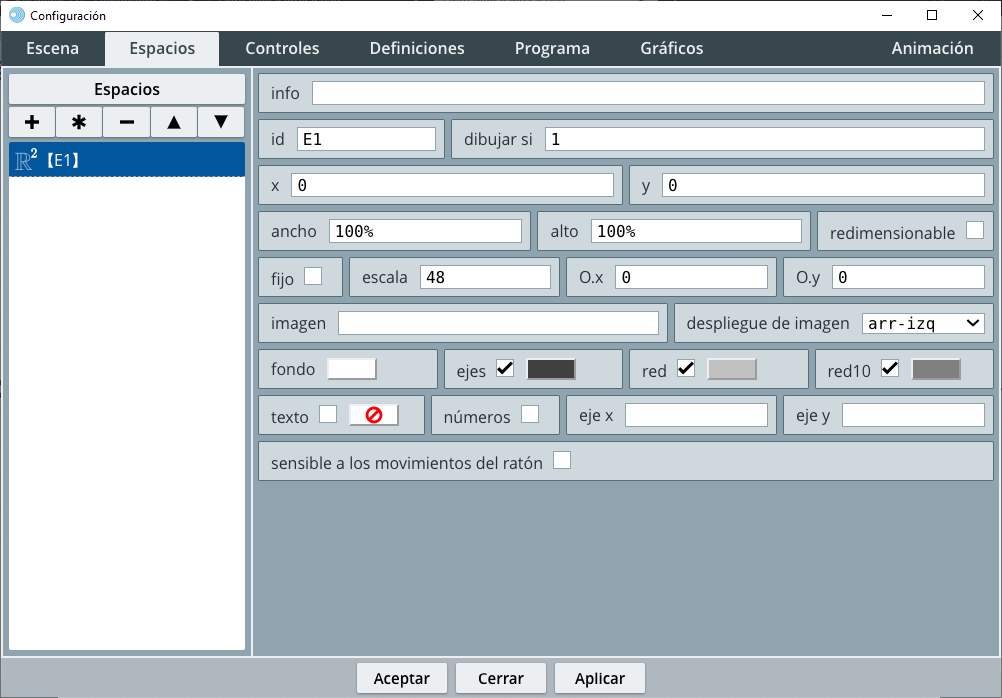
Las propiedades de un espacio bidimensional, las puedes consultar en el siguiente texto:
Iniciamos nuestra primera actividad, diseñando espacios cartesianos bidimensionales.
Inicialmente, reconfiguramos el espacio de trabajo para que quede con un fondo blanco. Luego insertamos un espacio $ℝ^2$ (bidimensional) en la esquina superior izquierda, cuyo tamaño es el 25% del área de trabajo. El procedimiento lo puedes observar en el siguiente vídeo.
Resumiendo el vídeo, observamos que cambiamos las dimensiones de la escena (selector Escena) o, si se prefiere, espacio de trabajo, a $800\times 600$ pixeles. El tamaño de la escena depende de su contenido, que irás cambiando a medida que produzcas nuevo material digital interactivo.
Posteriormente, desactivamos en el espacio de trabajo (selector Espacios) las casillas ejes, red y red10, además de fijar el espacio, todo ello con el propósito de dejar un espacio de trabajo limpio. Finalmente, creamos un espacio nuevo (haciendo clic en el botón +), al cual sólo le cambiamos el tamaño (ancho y alto) al 50%, es decir, con un área del 25% del espacio de trabajo. Obteniendo, hasta ahora, la siguiente escena:
Los dos espacios restantes (tridimensional y el tipo HTMLIFrame), los insertamos tal como se muestra a continuación:
Observa que el espacio $ℝ^3$ es, también, del 25% del tamaño de la escena, mientras que el HTMLIFrame es del 50%. A diferencia del primer espacio insertado, estos dos los ubicamos en posiciones diferentes; por ejemplo, el espacio tipo $ℝ^3$ lo ubicamos en una abscisa (x) a partir de la mitad de la escena, mientras que el HTMLIFrame en una ordenada (y) a partir de la mitad de la escena.
Es importante, para la posición de objetos, tener en cuenta que los valores de $x$ aumentan hacia la derecha y los de $y$ hacia abajo, teniendo el origen $(0,0)$ en la esquina superior izquierda del espacio de trabajo. Lo anterior no significa que los puntos geométricos del espacio $ℝ^2$ se comporten igual, éstos se rigen por las coordenadas tradicionales de un plano cartesiano.
En los espacios bidimensionales es posible incluir contenidos de tipo gráfico (funciones, ecuaciones, objetos geométricos), controles, imágenes. Y, como ocurre en nuestra primera actividad, podemos incluir varios espacios. Para nuestro ejemplo, hemos dibujado una función lineal ($y=x$), procedimiento que se muestra en la siguiente imagen animada:

Seguramente ya habrás observado que en los selectores, excepto los de Escena y Animación, aparecen unos controles en la esquina superior izquierda, tal como lo muestra la .
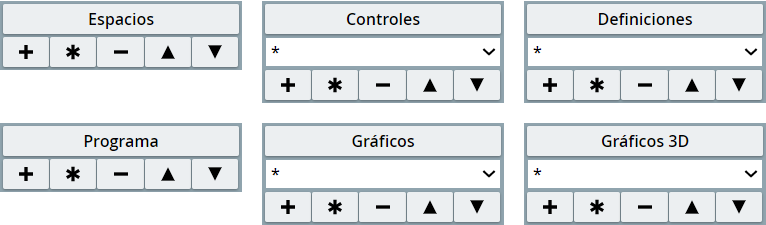
Este panel permite crear nuevos elementos, seleccionar los elementos a editar, duplicar elementos, eliminarlos o alterar el orden de los mismos, dependiendo del selector en el que nos encontremos. A continuación, explicamos el uso de este panel, para el selector Gráficos.
 Este botón gris claro, con la palabra Gráficos dentro, abre una ventana de edición de texto, donde puedes realizar la edición manual de todos los gráficos que hayas creado en un interactivo. Por ahora, no verás su utilidad; sin embargo, cuando tengas una escena con un gran número de gráficos te darás cuenta de lo importante de esta opción de edición. Por ejemplo, en la animación anterior habrás notado que el gráfico $y = x$ se dibujó en el espacio de trabajo
Este botón gris claro, con la palabra Gráficos dentro, abre una ventana de edición de texto, donde puedes realizar la edición manual de todos los gráficos que hayas creado en un interactivo. Por ahora, no verás su utilidad; sin embargo, cuando tengas una escena con un gran número de gráficos te darás cuenta de lo importante de esta opción de edición. Por ejemplo, en la animación anterior habrás notado que el gráfico $y = x$ se dibujó en el espacio de trabajo E1, lo que obligó a cambiar el espacio de destino a E2. Cuando tenemos un gran número de gráficos es más fácil hacer este tipo de cambios, desde la ventana de edición de texto. Este botón abre una ventana que permite, a través de un menú, agregar un gráfico.
Este botón abre una ventana que permite, a través de un menú, agregar un gráfico.
 Este botón permite duplicar el gráfico previamente seleccionado.
Este botón permite duplicar el gráfico previamente seleccionado. Este botón permite eliminar el gráfico previamente seleccionado.
Este botón permite eliminar el gráfico previamente seleccionado. Estos botones permiten cambiar el orden en que aparecen los gráficos.
Estos botones permiten cambiar el orden en que aparecen los gráficos.Retornando a nuestra actividad, el contenido del espacio E2 es la función lineal $y=x$, la cual agregamos con el botón +. Adicionalmente, cambiamos el ancho de la línea de $1$ a $2$ y el color de la línea.
Si haces una exploración a los diferentes selectores, notarás que es frecuente la aparición de botones que permiten el cambio de color de un texto, un control o un gráfico.
Observa, a continuación, una escena interactiva que te permite realizar combinaciones de color. La escena corresponde a una versión anterior de DescartesJS, pero tiene la misma funcionalidad de la versión actual.
En esta primera práctica, el color amarillo, en formato hexadecimal, sería ffff00. Pero, si observas bien, notarás que es posible incluir transparencia al color seleccionado que, para la escena anterior no está activada. Veamos, en la siguiente escena, cómo se puede usar la transparencia.
El editor DescartesJS se encuentra en permanente revisión y actualización, en procura de incorporar nuevas herramientas y mejorar las existentes, por esto siempre es buena idea descargar e instalar la versión más actual, y disfrutar de las novedades de cada versión.
Una de las mejoras es la edición de los textos contenidos en las cajas de texto, por ejemplo, en la escena de la página siguiente, hemos simulado el editor de configuraciones, para el contenido de nuestro espacio bidimensional. Lo hemos hecho de tal forma que puedas cambiar la ecuación cuadrática $y=x^2$. DescartesJS permite incluir diversas ecuaciones matemáticas, incluidas las paramétricas, sin embargo, para la escena interactiva, sólo podrás cambiar la ecuación por otra de la forma y = [expresión en x]. Veamos algunos ejemplos con los cuales puedes practicar (recuerda hacer clic en el botón Aplicar para ver los cambios):
y=x^3y=0.5*x^2-3*x+1y=sen(4*x)y=sqrt(4-x^2)En el apartado en el que trabajemos los textos enriquecidos, notarás las mejoras significativas, que facilitan la escritura de textos simples y los de tipo científico.
En otro capítulo profundizaremos sobre las funciones que soporta el editor DescartesJS.
Recuerda hacer clic en el botón Aplicar para ver los cambios.
La mayoría de los controles de estos espacios son iguales a los de espacios bidimensionales, con algunas excepciones, a saber:
despliegue: al usar tres dimensiones, los objetos colocados en el espacio pueden estar unos frente a otros. Para determinar cuáles quedan frente a cuáles hay 2 métodos distintos:orden: pinta los objetos de atrás hacia adelante. Involucra menos cálculos y es el más rápido, pero suele fallar para objetos muy grandes.pintor: dibuja las partes de los objetos de atrás hacia adelante, dibujando primero los objetos que son tapados por otros. Involucra más cálculos y es más lento, pero es más preciso que el método orden.cortar: es un checkbox que por defecto se encuentra inactivo. Es útil cuando diversos objetos tridimensionales se intersectan entre sí, pues permite un correcto despliegue de los objetos. Si los objetos desplegados no se cortan, no es necesario marcar esta opción.Los espacios 3D se manipulan pulsando y arrastrando. De esta forma se producen giros para poder visualizar los objetos desde diferentes perspectivas. Si se pulsa el botón derecho del ratón y se arrastra hacia arriba mientras éste está pulsado, se realizará un acercamiento. Si el arrastre es hacia abajo, se realizará un alejamiento.
Puedes practicar añadiendo un gráfico en el selector Gráficos 3D pero, para nuestra actividad, es suficiente con seleccionar el gráfico superficie.
En la siguiente escena interactiva hemos incluido un menú con varios de los gráficos de este selector. Prueba con algunos de ellos y, en algunos casos, notarás que aparecen cuadros de texto para los parámetros Nu y Nv, que puedes aumentar de valor para una mejor resolución del gráfico, sin embargo no exageres porque puedes bloquear la escena, usa valores entre $20$ y $30$.
Habrás notado, al cambiar los valores de Nu y Nv, que algunos gráfico 3D se construyen como una malla compuesta de varias superficies; por ejemplo, el cilindro se dibuja con siete rectángulos (Nu = 7) que, obviamente, poco se parece a un cilindro; por ello, al aumentar el valor de Nu (80, por ejemplo), la resolución obtenida es mucho mejor.
Por su parte, la esfera se construye con triángulos, trapecios y rectángulos, en la que los campos Nu y Nv, respectivamente, definen el número de paralelos y de meridianos. Utilizar valores de $80\times 80$ ($6400$ superficies) para Nu×Nv, el gráfico se verá más parecido a una esfera, pero al exagerar el valor de estos parámetros puede resultar en un interactivo de lenta actualización; puedes hacerlo con una resolución de $30\times 30$, que da como resultado una esfera de apariencia aceptable.
En este espacio podemos incorporar una página web con formato html. Este tipo de espacio contiene un campo archivo que los demás no tienen. En él se ingresa la dirección web o local a un archivo html que se desea abrir en dicho espacio que, para nuestra actividad, es https://www.youtube.com/embed/vd5VahGPWus, la cual es una dirección a un vídeo de YouTube, donde la expresión vd5VahGPWus es el código asignado por YouTube para identificar el vídeo.
Hasta aquí terminamos la actividad propuesta en este capítulo. Una vez tengas tu escena interactiva, debes guardarla en una carpeta (podrías llamarla actividades). El nombre de la escena es actividad1. DescartesJS le agrega la extensión html en caso de no escribirla explícitamente, lo que significa que la escena guardada puede abrirse desde tu navegador.
Al final del capítulo tendrás una tarea propuesta, que puedes llamarla name.html, donde name es tu nombre; por ejemplo: cocampo, que es la abreviatura de Carlos Ocampo.
La posibilidad de añadir espacios sobre un área de trabajo, nos ha permitido diseñar algunas aplicaciones, de las cuales compartimos dos. La primera es un puzle giratorio, cuyas imágenes son descargadas de flickr; lo interesante es que se logra la disposición de las fichas del puzle gracias a la incorporación de 24 espacios 2D (uno por cada ficha).
La segunda aplicación es una lupa (E1) que se desplaza sobre un mapa (E0). Esta aplicación, a su vez, la hemos utilizado para una actividad evaluativa, que puedes consultar en http://reddescartes.org/documentacion/?s=lupa
Para terminar este apartado, te proponemos el siguiente ejercicio:
Diseñar una escena con dos espacios.
El primero debe ser un espacio 2D o 3D, cuyo contenido es un gráfico cualquiera. El segundo es un espacio HTMLIframe que debe contener un vídeo o una página web cuyo contenido hace referencia al gráfico del primer espacio. En la siguiente escena verás un ejemplo.
El ejemplo consta de un espacio 3D con el gráfico de un toroide (se ha cambiado el color del fondo a blanco) y un espacio HTMLIframe correspondiente a una entrada de Wikipedia que contiene información sobre este gráfico.
¡Recuerda que puedes mover el espacio y por consiguiente el toroide, con clic izquierdo sostenido!
Al terminar este capítulo, habrás diseñado los siguientes objetos interactivos:
En este objeto interactivo incorporamos imágenes en el selector Espacios y en el control tipo botón. Por primera vez, haremos uso del condicional dibujar si, algunas expresiones simples con variables matemáticas y la escritura de textos simples.
En este objeto interactivo incorporamos una animación. Es una primera incursión al uso de algoritmos, que permitan realizar actividades iterativas.
Es común que el primer objeto multimedia que se nos ocurre incorporar a un diseño con destino a la web sea una imagen. Las imágenes que usamos son fotografías, diseños, gráficos, fondos y, en ocasiones, imágenes animadas.
Dada esta tendencia de diseño, es importante conocer los diferentes formatos que podemos usar en el editor DescartesJS y algunas recomendaciones para evitar la carga de imágenes de gran peso o de pobre resolución que, en términos técnicos, se refiere a los niveles de compresión (tamaño) y al tratamiento de color (calidad).
Actualmente, los formatos de imagen se agrupan en dos. La primera agrupación son las imágenes pixeladas o de mapa de bits, en la que un pixel o punto es un color; por ejemplo, si la imagen es de $8$ bits, significa que cada pixel puede tener hasta $256$ colores, una de $16$ bits puede lograr hasta $65,536$ colores por pixel. Obviamente, el segundo ejemplo es de mayor calidad y, en consecuencia, de mayor peso. Las diferencias de calidad la podemos observar entre los videojuegos de $8$ bits (Nintendo, por ejemplo) y los de $16$ bits (Super Nintendo, por ejemplo), tal como se aprecia en la .

Los formatos de imagen en esta primera agrupación que se pueden usar en el editor DescartesJS son: jpg, gif y png.
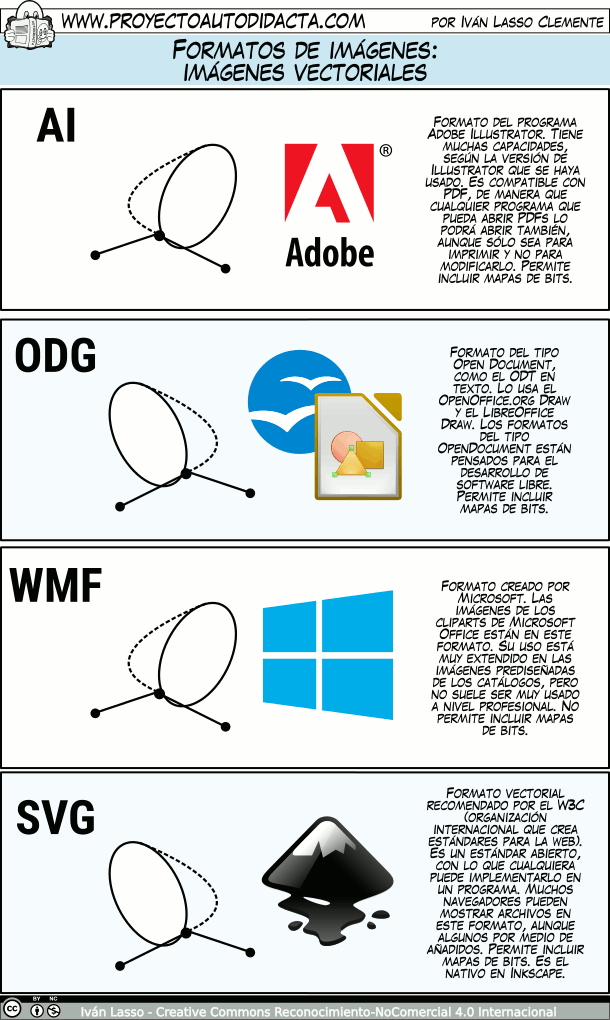
El segundo grupo corresponde a las imágenes vectoriales, que se construyen con elementos geométricos, como círculos, polígonos, muros, arcos, entre otros.
La ventaja de una imagen vectorial es que no pierde calidad al aumentar su tamaño, por contraste a las imágenes pixeladas que sí pierden calidad. En la , se puede apreciar esta gran diferencia.

El formato svg es el recomendado por el consorcio internacional de estándares para la web (W3C)El World Wide Web Consortium (W3C) es una comunidad internacional que desarrolla estándares que aseguran el crecimiento de la Web a largo plazo. Fue fundado en $1994$ para dirigir a la Web hacia su pleno potencial mediante el desarrollo de protocolos comunes que promuevan su evolución y aseguren su interoperabilidad. (crédito: http://www.masadelante.com/faqs/w3c)., formato que es ampliamente compatible con la web y en particular con el editor DescartesJS.
En la siguiente página, presentamos cuatro formatos de imágenes vectoriales.
A continuación, describimos los formatos de imágenes pixeladas que podemos usar con nuestro editor.
Las imágenes en este formato pueden contener entre $2$ y $256$ colores, es un formato muy popular en imágenes animadas. Dado este número de colores tan limitado, las imágenes que se obtienen son muy pequeñas y por tanto de bajo peso. En nuestros ejercicios, usaremos este formato para los botones (controles) e imágenes animadas.
Este formato soporta $16.7$ millones de colores ($24$ bits) y es el más empleado para las fotografíasLa sigla JPEG (Joint Photographic Expert Group) surge de la reunión que tuvo lugar en $1982$ entre un grupo de expertos en fotografía, que trabajaban principalmente en las formas de transmitir información (imágenes fijas o animadas). En $1986$, el ITU-T desarrolló métodos de compresión destinados al envío de faxes. Estos dos grupos se unieron para crear el Grupo Conjunto de Expertos en Fotografía (JPEG) (crédito: https://es.ccm.net).. El nivel de pérdidas en calidad depende del nivel de compresión. Es un formato muy usado en los diseños de la web.
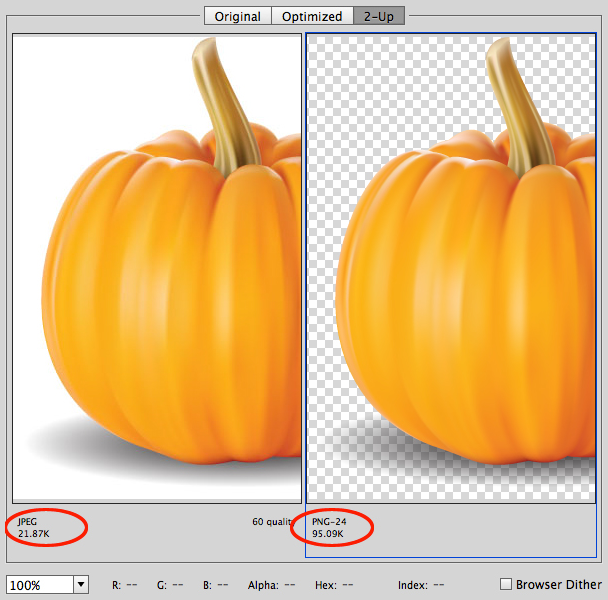
Este formato utiliza una compresión sin pérdidas, permitiendo imágenes con color verdadero, escala de grises y paleta de $8$ bits, fue desarrollado en $1995$ como una alternativa gratuita al formato GIF, cuyos derechos pertenecen a Unisys (propietario del algoritmo de compresión LZW) y a quien los editores de software deben pagar regalías por usar este formato.
PNG es un acrónimo recursivo de "PNG No es GIF" (crédito: https://es.ccm.net). Este formato goza de popularidad por permitir transparencias en sus imágenes, lo cual significa un mayor peso, tal como se muestra en la .
¡Advertencia! En el editor DescartesJS, es importante que hagas coincidir mayúsculas y minúsculas, tanto del nombre de la imagen como de su extensión. Es común que al descargar una imagen de la web, la extensión se escriba en mayúscula. Si no atiendes esta advertencia, al publicar tu objeto interactivo, las imágenes no se visualizarán.
Para lograr el diseño de los objetos interactivos en la actividad propuesta en este capítulo, te hemos compartido un grupo de imágenes en diferentes formatos (png, gif, jpg) y para diferentes propósitos (fondos, botones, marcos e imágenes animadas). Estas imágenes las puedes descargar en este enlace: imágenes
Para el primer objeto usaremos dos espacios, uno para los marcos (bordes) del espacio, y otro para los fondos. Recurriremos a la propiedad de transparencia del color del fondo, de tal forma que sólo sean visibles los marcos. Por ejemplo, uno de los marcos es una pantalla de televisión (17.png en la carpeta marcos), al usar transparencias, podemos lograr algo como esto (has clic en el botón inferior, para reproducir el vídeo):
En el ejemplo anterior, lo que hicimos fue crear dos espacios. El primero, es un espacio del tipo HTMLIframe cuya página, de nuevo, es un vídeo de YouTube. En el segundo espacio se encuentra lo novedoso de la escena, pues se trata de un espacio $ℝ^2$ sobrepuesto al primero, en el que hemos puesto una transparencia total al color de fondo, además de una imagen de borde en formato png (permite la transparencia). La imagen seleccionada (carpeta marcos), presenta una imagen de un televisor antiguo, con transparencia en la zona correspondiente a la pantalla, de tal forma que se logra un efecto bastante realista. Algo similar haremos en nuestro primer objeto interactivo.
¡Sugerencia! El esfuerzo realizado para crear un objeto interactivo, se puede ver frustrado al usar contenidos multimedia externos que, en el futuro, presentan enlaces rotos o cambios en los protocolos de acceso. Esta situación es común en los vídeos de servicios como YouTube o Vimeo. Sugerimos, entonces, usar vídeos en local o de tu propio canal de YouTube.
Por otra parte, en el caso de las imágenes, es importante evitar cualquier violación de derechos de autor. Trata de diseñar tus propias imágenes o, al menos, usar repositorios de dominio público. Las imágenes que hemos compartido, provienen de los siguientes repositorios:
Puedes consultar estos repositorios y elegir otras imágenes para la tarea final de este capítulo. Igualmente, puedes investigar qué otros repositorios de imágenes de dominio público o gratuitos hay en la red.
Nuestra primera tarea es diseñar el espacio que va a contener los fondos de pantalla. En realidad, tendremos que usar varios espacios $ℝ^2$ para mostrar varios fondos. Por ahora, nos preocuparemos por el primer espacio, para ello, observa la .
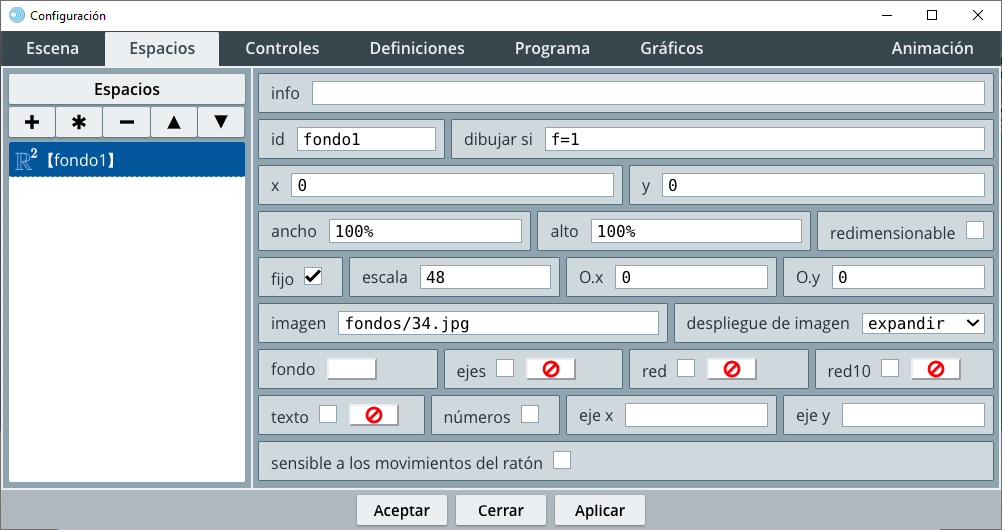
Si observas con detalle, notarás la siguiente configuración de este primer espacio, que puedes lograr con estos pasos:
ejes, red y red10) y hacemos clic en el botón aplicar.actividad2.html, debes hacerlo antes de continuar la configuración del espacio, pues así es que te aparecerá la imagen de fondo.34.jpg de la carpeta fondos. Es importante que se escriba correctamente la ruta relativa; para el ejemplo, la imagen se encuentra en la carpeta fondos, la cual debe estar en el mismo directorio del archivo html.despliegue de imagen la opción expandir.Ahora, resumimos lo anterior y te explicamos cómo usar una variable de control, en el siguiente vídeo:
Observa que hemos vinculado una variable f con valor de 1 en el selector Programa. Continuemos, entonces, con el diseño de nuestra actividad.
dibujar si, escribimos f=1. Esto significa que el espacio se dibujará siempre que está igualdad sea verdadera. Como en el selector Programa asignamos 1 a esta variable, la condición dibujar si es verdadera. En el vídeo cambiamos la condición a f=2, lo cual es falso, por ello, no se dibujó el espacio.Es posible que el vídeo te haya dejado anonadado 😊. Algo normal, pues hemos usado varias de las utilidades de la herramienta DescartesJS, como son las variables (selector Programa) y los botones (selector Controles). Pero, no te preocupes, pues todo es muy sencillo y sólo necesitas un mínimo de lógica, que explicamos a continuación.
Continuemos, entonces, con los pasos de nuestra actividad.
* clonamos los dos espacios. En cada espacio cambiamos su identificador (id) por E2 y E3, las imágenes del fondo a utilizar, para el ejemplo, son fondos/35.jpg y fondos/36.jpg (no olvides la dirección relativa de las imágenes) respectivamente. Además, cambiamos el condicional dibujar si por f=2 y f=3.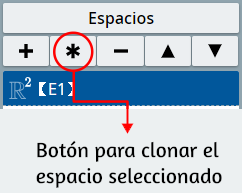
controles, el cual estaría por encima de los tres anteriores. Este último espacio es el que se observaría al hacer clic en el botón aplicar, lo cual nos obligó a asignarle transparencia total al fondo (observa el vídeo), de tal forma que se puedan ver los espacios E1, E2 o E3, según se seleccione. Observa la que te da una idea de esta situación.f, de tal forma que podamos observar los espacios E1, E2 y E3 de acuerdo al valor de esta variable. Estos botones los creamos en el selector Controles. 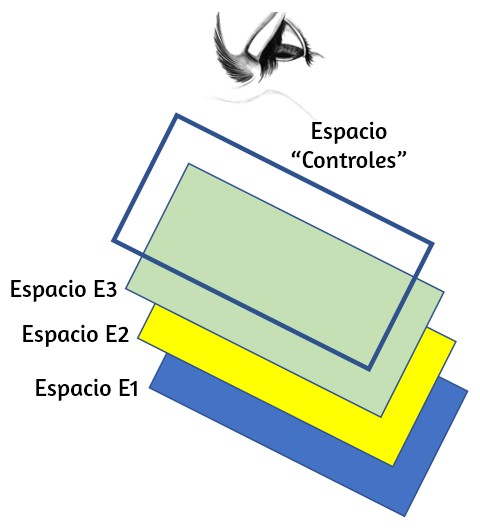
Con el botón + creamos el primer control, seleccionando la opción botón, es decir, cuando aparece el cuadro de diálogo, cambiamos el tipo del control de pulsador a botón.
interior de la escena, las otras opciones las explicaremos más adelante. Por omisión, los botones se asignan al primer espacio (en este ejemplo, E1) que, como ya explicamos, debemos cambiar al espacio controles. Podríamos dejar el control con el diseño original; sin embargo, le vamos a asignar la imagen de la carpeta botones/, llamada der6.gif. Esta imagen tiene un tamaño de $37\times 37$ pixeles que es importante para la siguiente configuración.
Si observas el contenido de la carpeta botones, notarás que la imagen der6.gif está acompañada de otra imagen llamada der6_over.gif. Cuando estas imágenes están presentes, significa que al pasar el ratón sobre (over) el botón, presentará un cambio de imagen.
La siguiente configuración debemos hacerla en el parámetro expresión, la cual cuenta con cuatro valores. Los dos últimos corresponden al ancho y alto de la imagen, es decir, $37\times 37$. Los dos primeros números definen la posición de la imagen dentro del espacio controles (recuerda que la $x$ crece de izquierda a derecha y la $y$ de arriba a abajo) ; por ejemplo, si la escena es de un tamaño de $970\times 550$ pixeles, una posición de x=953 y y=513 dibujaría el botón en la esquina inferior derecha del espacio ¿por qué? Prueba varias posiciones, antes de continuar con la actividad.
Para nuestra actividad (observa el vídeo), el valor de la expresión es: (180,80,37,37).
acción para cuando hagamos clic sobre él. Esa acción es calcular, pero ¿calcular qué? Nuestro propósito es que haya un cambio de fondo o, sí se prefiere, de espacio. Como los espacios se muestran de acuerdo al valor de la variable f, necesitamos que la acción incremente el valor de f, que inicialmente es 1. En el cuadro de diálogo parámetro, definimos esta acción con la expresión f = f+1 ¿muy extraño? Seguramente que sí para el matemático, pues f no puede ser igual a f+1 ¡es un absurdo! He aquí un primer concepto de programación que debes entender.La expresión f = f+1 no es una igualdad ¡es una asignación!, que significa lo siguiente: al valor de la variable f le sumamos 1 y el resultado de está operación se lo asignamos, de nuevo, a la variable f, es decir, la asignación funciona de derecha a izquierda. La confusión generada por esta expresión, motivó a que en algunos lenguajes de programación se utilicen expresiones como f:=f+1, para no confundirla con una igualdad. Poco a poco te acostumbrarás a estas asignaciones.
Así las cosas, cuando hagas clic en aplicar aparecerá nuestro botón con la acción configurada, de tal forma que al hacer clic en el botón por primera vez, el valor de f será 1+1, el siguiente clic cambia el valor de f a 3, y así sucesivamente. Recuerda que el espacio E2 se dibuja si, f=2 y E3 si f=3. Pero como sólo tenemos tres espacios, no podemos permitir que el botón siga sumando uno a la variable, por ello, en el cuadro de diálogo dibujar si, escribimos la expresión f<3, que significa que si f ya tomó el valor de 3, el botón no se dibuja.
f=3 estará mostrando el espacio E3. Necesitamos otro botón para que reduzca el valor de f y muestre los espacios E2 y E1. Para ello, clonamos el primer botón y hacemos los siguientes cambios: la imagen por izq6.gif, la posición por (60,80,37,37) que lo ubica a la izquierda del primer botón, la acción por f=f-1 (reduce el valor de f) y el condicional por f>1, es decir, se dibuja cuando aparezca el espacio E1.Amplía la actividad $2$ a cinco fondos y la guardas así: name2.html, donde name... bueno, ya sabes. Recuerda que el espacio controles debe ir al final, para ello, usa las flechas del panel del selector de Espacios.
Si quieres conocer más sobre la configuración de los botones, lee el siguiente texto:
Dado que el procedimiento es similar, es suficiente que observes el siguiente vídeo:
Algunos aspectos del vídeo a tener en cuenta:
controles, por ello, lo hemos desplazado usando el panel del selector Espacios.texto, que profundizaremos más adelante.Amplía la tarea 2, incluyendo cinco marcos.
La historia de la animación es rica en descubrimientos y en invenciones. Uno de los primeros descubrimientos fue "la persistencia de la visión o retiniana", descubierto por Peter Mark Roget y estudiada por Joseph-Antoine Ferdinand Plateau, que inventa el FenaquistoscopioPlateau definió el principio de la persistencia de los estímulos luminosos en la retina (Persistencia de la visión) y determinó que su duración es de una décima de segundo. Este tiempo no es constante, sino que aumenta cuando el ojo está adaptado a la oscuridad; ese es el mecanismo por el cual, a partir de imágenes fijas, percibimos la sensación de movimiento durante la proyección de una película.
En $1832$, Plateau inventó un primitivo dispositivo estroboscópico, el fenaquistiscopio, el primer dispositivo capaz de proporcionar la ilusión de una imagen en movimiento a partir de una secuencia de imágenes fijas. Compuesto de dos discos coaxiales, uno con pequeñas aberturas radiales y equidistantes, a través de las cuales el espectador puede mirar y otro disco conteniendo una secuencia de imágenes fijas impresa. Cuando los dos discos rotan a la velocidad adecuada, la sincronía entre las aberturas y las imágenes crea una ilusión de animación de las imágenes. La proyección de fotografías estroboscópicas, creando la ilusión de movimiento, daría lugar, eventualmente, a la invención del cinematógrafo de los hermanos Lumière (https://es.wikipedia.org/wiki/Joseph-Antoine_Ferdinand_Plateau)..
Nuestro propósito, en este libro, no es hacer un discurso sobre la historia de la animación; sin embargo, el dispositivo de Plateau llama la atención, en tanto que el éxito de las primeras animaciones se debió a la comprensión de cómo percibimos las imágenes, en especial aquellas que se presentan en una sucesión de secuencias, las cuales entremezclan lo percibido con lo recién percibido (una décima de segundo antes), pero, que sea el dispositivo de Plateau (simulado con DescartesJS) el que hable por sí sólo:
Tampoco es nuestro propósito realizar un curso de animación. Lo que vamos a presentar es cómo podemos incorporar algunas animaciones en nuestros objetos interactivos y, así, desarrollar la segunda actividad planteada al inicio del capítulo.
Una primera opción es incorporar animaciones prediseñadas en nuestro objeto interactivo, como la que se muestra a continuación, diseñada por Matt Boldt:
Otra opción es incorporar un objeto flash (no recomendado en la actualidad) o un gif animado, como el de la :

Esta última opción fue muy popular en la animación para las páginas web, especialmente para iconos, botones, menús y banners.
Iniciamos nuestra última actividad, de este capítulo, diseñando el fondo de nuestro espacio de trabajo.
ejes, red y red10, y activamos el checkbox fijo, este último para evitar el desplazamiento de las imágenes que vamos a incorporar.patrones/ (la imagen 15.jpg). Si observas el tamaño de esta imagen, notarás que es de $96\times 96$ pixeles, muy pequeña para cubrir nuestro espacio de trabajo (observa la ). DescartesJS cuenta con una opción que permite replicar la imagen sobre todo el espacio, para ello, selecciona la opción mosaico del menú despliegue de imagen.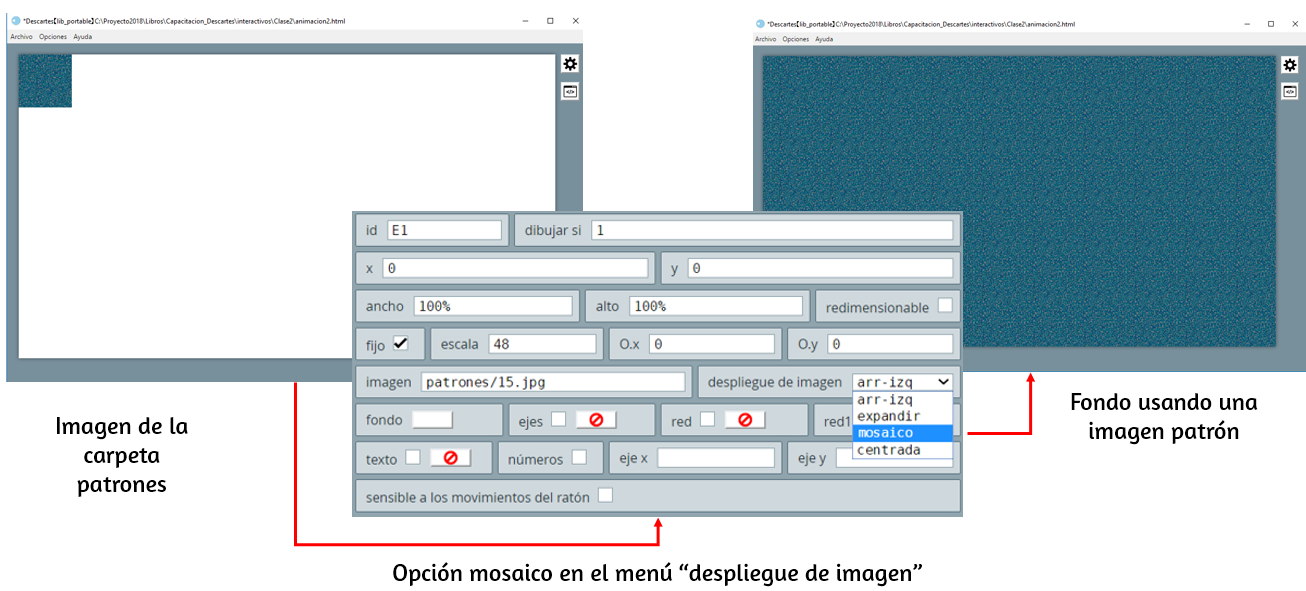
Para que entiendas cómo se logra obtener el fondo anterior, debes saber que los patrones o mosaicos más conocidos son las teselaciones, que se basan en la repetición.
Una única plantilla, azulejo o célula, se combina mediante duplicados sin cambios o modificaciones [...] Otros patrones, como la teselación de Penrose y los patrones indios Pongal o Kolam, usan simetría, que es una forma de repetición finita, en lugar de una traslación, que puede repetirse hasta el infinito. Los patrones fractales también utilizan aumentos o escalas que producen un efecto conocido como autosimilaridad o invariancia de escala. Algunas plantas, como los helechos, incluso generan un patrón usando una transformación afín que combina la traslación, con el escalado, la rotación y la reflexión.https://es.wikipedia.org/wiki/Patrón_(estructura)
Una teselación que solemos usar es la cenefa, tal como lo puedes observar en la siguiente escena interactiva del Proyecto Canals:
Continuemos con el diseño de nuestra actividad en la que tenemos, hasta el momento, el fondo de nuestro espacio de trabajo.
+) un dodecaedro cuyo color (el que desees) tendrá una ligera transparencia (observa la ) y activamos el checkbox aristas.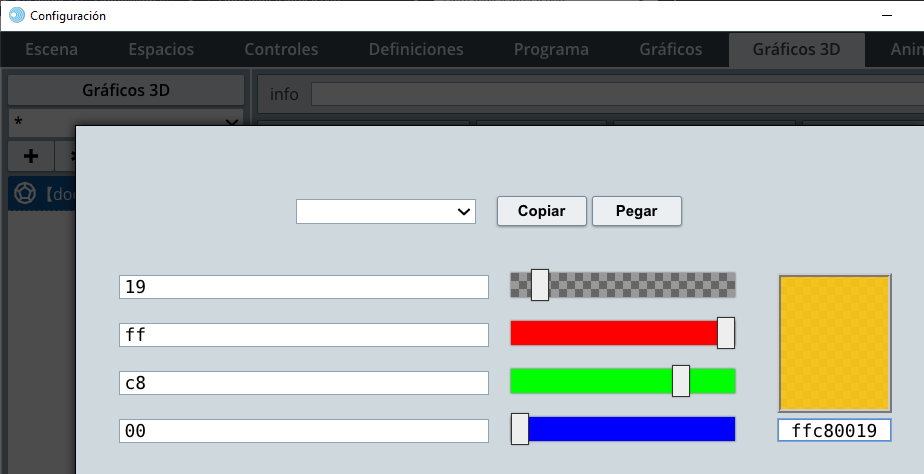
140, aunque podrás tener otro gusto con el cual no vamos a discutir... por ahora.Hasta este momento de diseño de la actividad, debes tener algo así como lo que muestra esta imagen:

dodecaedro, esta imagen debe tener transparencia, pues una imagen sin ella se vería bastante fea en nuestra actividad. Un formato de imagen con estas características es del tipo png o svg. En nuestra actividad, hemos usado una de formato svg, que puedes descargar aquí (si te aparece la imagen, con clic derecho la puedes guardar en tu carpeta de imágenes con el nombre que quieras).Nosotros la tenemos con el nombre gallina (recurrimos a nuestra creatividad para asignar nombres). Muy bien, ahora la vamos a agregar desde el selector Gráficos, con la ruta imagenes/gallina.svg en el campo de texto archivo y en la posición dada por la expresión (6,3.5,.6,.6).
La expresión anterior, merece este apartado antes de continuar con nuestra actividad, pues a diferencia de los botones, la posición de las imágenes si obedecen a las coordenadas cartesianas.
Este gráfico consiste en una imagen tipo jpg, png, svg o gif que puede insertarse en nuestro objeto interactivo. La imagen debe estar en la misma carpeta que el interactivo o en una subcarpeta. La expresión es un campo de texto en el que se introducen las coordenadas (cartesianas) donde habrá de mostrarse la imagen en el interactivo. Por defecto son dos coordenadas y corresponden a dónde estará situada la esquina superior izquierda de la imagen. No obstante, se pueden introducir cuatro entradas en los paréntesis, en donde la tercera y cuarta entradas corresponden al factor de escala del ancho y alto de la imagen. En caso de definir las cuatro entradas, las dos primeras ya no marcan la esquina superior izquierda de la imagen, sino su centro. La tercera y cuarta entradas (las escalas horizontal y vertical) pueden adoptar valores negativos, en cuyo caso la imagen se invertirá horizontal y/o verticalmente.
De acuerdo a lo anterior, analiza las siguientes imágenes en las que hemos puesto la expresión (debajo de ella) que ha permitido dibujarlas tal como se muestra en la .
La imagen del centro está en las coordenadas (0,0) del plano cartesiano, por ello se ve en el centro de la escena, y su escala (1,1) indica que es el tamaño real de la imagen. Por otra parte, la imagen que está encerrada en el círculo, se encuentra en la coordenadas (-5,4) (ver el punto amarillo) y reducida a la mitad de su tamaño (-.5,.5). El signo menos del primer número indica que se invierte horizontalmente.
Observa la imagen inferior derecha, la cual tiene una desproporción. Ello obedece a que le dimos una escala horizontal del doble de la vertical, (.6,-.3).
¿Complejo de entender? Quizá, pero no tanto. Te sugerimos practicar con varias posiciones y escalas y así, seguramente, lo comprenderás mejor.
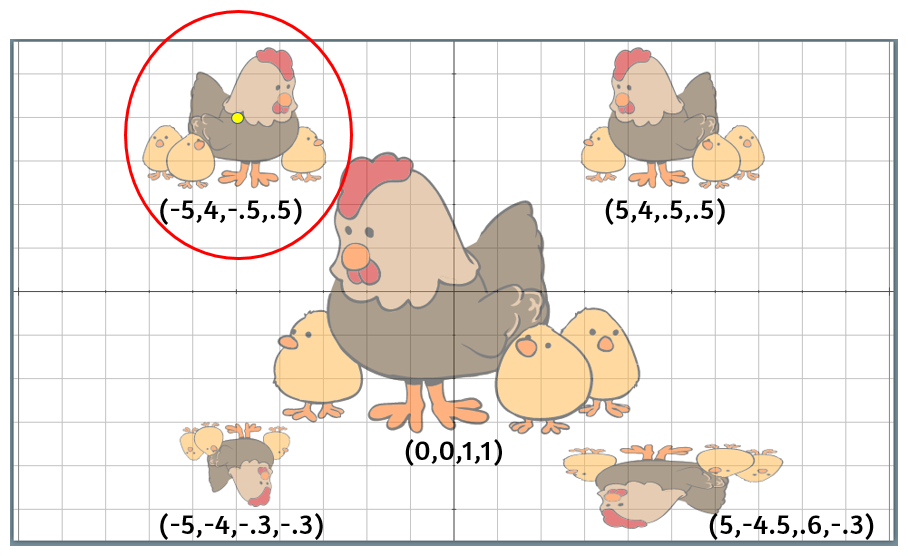
(6,3.5,.6,.6) que, seguramente, ya estarás en capacidad de comprender su significado, tanto de la posición de la imagen en el plano cartesiano como la escala utilizada.Hay otras opciones para configurar la imagen que dejamos para tu consulta, en el texto de la página siguiente.
Si quieres conocer más sobre la configuración del gráfico imagen, lee el siguiente texto y continúa practicando:
Nuestra actividad está a punto de terminar, sólo nos falta animar el dodecaedro, pero antes queremos destacar el diseño obtenido, pues el objeto 3D sobre un plano 2D lo hemos usado en una escena diseñada por Josep Mª Navarro Canut, que trata sobre superficies paramétricas. Disfruta de ella, seleccionando e interactuando con cualquiera de las superficies dispuestas en el menú.
El editor de configuraciones de DescartesJS cuenta con un selector de Animación que, inicialmente, puedes consultar en el siguiente texto:
Más adelante profundizaremos en los algoritmos de DescartesJS, mientras tanto vamos a explicar cómo logramos animar nuestro dodecaedro.
E2.rot.z = E2.rot.z + 3, en el espacio 3D de DescartesJS, los ejes cartesianos tienen la siguiente configuración: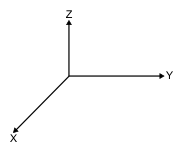
E2.rot.z significa la rotación del espacio E2 (así tenemos identificado nuestro espacio tridimensional, dale una mirada al selector Espacios) alrededor del eje $z$. La asignación repetitiva E2.rot.z = E2.rot.z + 3, significa que sumaremos 3º a dicha rotación.E2.rot.y = E2.rot.y + 1, en este caso, la asignación indica que sumamos 1º a la rotación del espacio E2 alrededor del eje $y$.Por defecto las rotaciones alrededor de $z$ y $y$ son cero, lo que significa que las asignaciones anteriores se ejecutarán mientras, E2.rot.z<10 (observa la imagen anterior), es decir, tomará valores de $3$, $6$ y $9$ y allí termina; sin embargo, como activamos el checkbox repetir, el proceso vuelve y se repite indefinidamente.
Comprendemos que puede ser un poco complejo si no tienes conocimientos básicos de programación, pero no te preocupes que en el próximo capítulo haremos una explicación detallada de tres estructuras básicas de programación: asignación, condicional simple y bucles o ciclos "hacer-mientras".
Animar, imagen botones/1.gif y expresión (0,0,150,40). Luego, en el menú acción seleccionas animar¡Eso es todo! Ya tienes la segunda actividad diseñada.
Suponemos que te has sorprendido con el objeto interactivo anterior, pues apareció otra animación no mostrada en la actividad inicial ¡Fue adrede!, sólo para explicar cómo incluir gifs animados en una escena de DescartesJS.
Ya habíamos dicho que DescartesJS admite imágenes en formato svg, jpg, png y gif; sin embargo, un gif animado aparecerá estático. Pero, hay un pequeño truco que podemos usar, consiste en agregar un espacio HTMLIFrame e incluir el gif animado.
Haz lo siguiente:
323 y alto 350 (las dimensiones del gif).
x = 10 y en y = 40.gifs/5.gif y, ahora sí, ¡Eso es todo!A propósito de gifs animados, ¿qué tal este puzle "Memoriza"?:
Al terminar este capítulo, habrás resuelto los siguientes problemas:
Al leer los problemas planteados, quizá algunos se sientan desanimados, pues no esperaban nada de matemáticas y menos de programación. No obstante, como ser humano que eres siempre aplicas algo de lógica en tus decisiones, desde la simple decisión de ir al trabajo a la más compleja que es decidir sobre tu proyecto de vida. No te preocupes que este curso está diseñado para tratar conceptos básicos o, si se prefiere, elementales de programación. Sabías, por ejemplo, que Edsger Dijkstra, un experto en programación (considerado por algunos como el padre de la programación estructurada), nunca usó un ordenador para ejecutar y verificar sus algoritmos... pues, todo se reduce a la lógica... la lógica de programaciónAunque parezca irónico, Dijkstra, uno de los mayores desarrolladores de software de su época, evitó el uso de computadores en su trabajo durante décadas. Cuando, finalmente, sucumbió a la tecnología, únicamente utilizó los ordenadores para enviar correos electrónicos y hacer búsquedas en la red. Dijkstra nunca utilizó un computador para realizar ninguno de sus trabajos, todos ellos fueron realizados a mano. (crédito: https://es.wikipedia.org/wiki/Edsger_Dijkstra)..
Para que quedes más tranquilo, algunos científicos de la computación (Dijkstra, Jacopini, Böhm, von Neumann, ...), estuvieron de acuerdo en afirmar que todo programa se puede realizar combinando sólo tres estructuras lógicas o de control:
La herramienta DescartesJS permite resolver los problemas anteriores, utilizando varias alternativas y con un código propio para elementos básicos como selección, lectura y escritura de datos. En las estructuras iterativas, además del algoritmo clásico Hacer-Mientras (Do-While), el uso de familias en los selectores Gráficos, permite desarrollar actividades iterativas (repetitivas) que simplifica muchas situaciones.
No hay consenso sobre la definición formal de "algoritmo", no obstante, en forma general, se puede decir que es un conjunto de instrucciones o reglas bien definidas, ordenadas y finitas que permiten llevar a cabo una actividad mediante pasos sucesivos que no generen dudas a quien deba hacer dicha actividad.
En matemáticas, lógica, ciencias de la computación y disciplinas relacionadas, un algoritmo (del griego y latín, dixit algorithmus y este del griego arithmos, que significa «número», quizá también con influencia del nombre del matemático persa Al-Juarismi) es un conjunto prescrito de instrucciones o reglas bien definidas, ordenadas y finitas que permiten llevar a cabo una actividad mediante pasos sucesivos que no generen dudas a quien deba hacer dicha actividad. Dados un estado inicial y una entrada, siguiendo los pasos sucesivos se llega a un estado final y se obtiene una solución. En términos de programación, un algoritmo es una secuencia de pasos lógicos que permiten solucionar un problema. (https://es.wikipedia.org/wiki/Algoritmo).
Un algoritmo se puede representar de varias maneras: lenguaje natural, pseudocódigo, diagramas de flujo o en un lenguaje de programación. Para los problemas de este capítulo, usaremos el pseudocódigo y la herramienta DescartesJS para su solución.
Permite la transición de la solución de nuestros problemas a un lenguaje de programación específico, el pseudocódigo es un conjunto de pasos claros que permiten llegar a la solución de un problema. A continuación, iniciamos la solución de los problemas planteados al inicio de este capítulo.
Una estructura secuencial es aquella en la que las instrucciones se ejecutan una después de la otra, en el orden en que están escritas, es decir, en secuencia. En una estructura secuencial se espera que:
se proporcione uno o varios datos, los cuales son asignados a variables para que con ellos se produzcan los resultados que representen la solución del problema que se planteó (https://www.uaa.mx).
Problema 1. A un estudiante se le aplican tres exámenes durante el semestre, cada examen tiene el mismo valor porcentual. Elabora un pseudocódigo y ejecútalo en DescartesJS para obtener el promedio de calificaciones.
Observa el pseudocódigo para la solución de este problema:
InicioLeer Nota1, Nota2, Nota3Hacer Suma = Nota1 + Nota2 + Nota3Hacer Prom = Suma/3Escribir PromFinLa secuencia o instrucción del tipo Hacer, como la cuarta instrucción del pseudocódigo anterior (Hacer Prom = Suma/3) es una asignación, que no se debe entender como una igualdad. Su interpretación debe ser de la siguiente forma: "se realiza la operación Suma/3, el resultado se asigna a la variable Prom". Como lo hemos reiterado antes, la asignación funciona de derecha a izquierda.
Para evitar este tipo de confusiones, algunos programadores prefieren usar la siguiente convención:
Prom ← Suma/3
En lenguajes de programación como Pascal o Delphi: Prom := Suma/3 o en lenguaje C: Prom /= 3, siempre buscando evitar la confusión y comprender que asignaciones como c = c + 1 son completamente válidasLa asignación c = c + 1 se conoce como contador, pues en una estructura iterativa (como veremos más adelante), a la variable c se le suma el valor de 1, N veces, es decir, si c es inicialmente cero, se le irá asignado los valores 1, 2, 3, ..., N..
Comprendido lo anterior, para ponernos a tono con la herramienta DescartesJS, en nuestros pseudocódigos usaremos la asignación Prom = Suma/3 (ver )
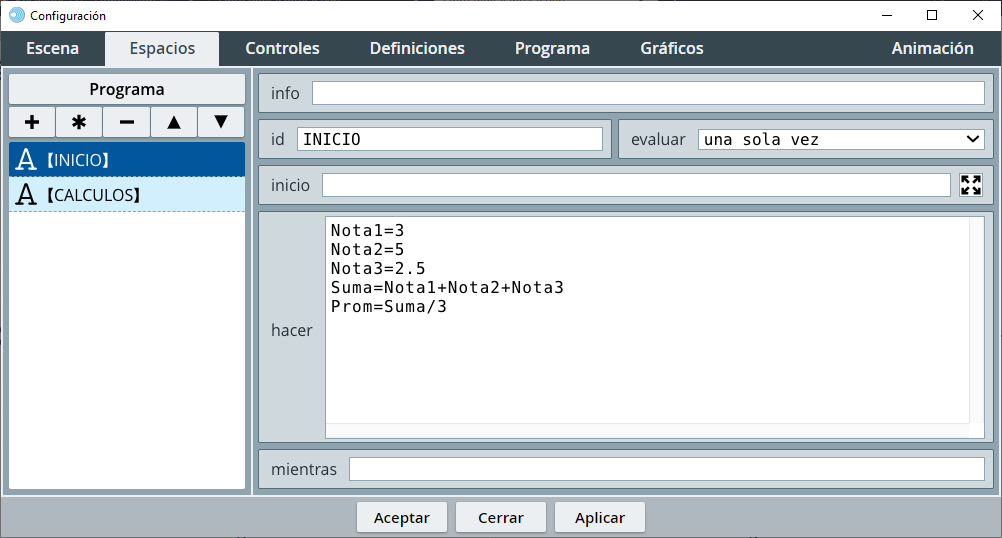
Puedes observar que hemos usado el selector Programa pues, obviamente, estamos programando. También habrás notado que elegimos el algoritmo INICIO evaluado una sola vez, pues para nuestro problema cumple con lo enunciado: Leer las notas y calcular su promedio.
Seguro ya estarás preguntándote qué ocurrió con las instrucciones Inicio, Escribir y Fin. Tanto Inicio como Fin, en una estructura secuencial, son convenientes en el pseudocódigo; sin embargo, en el código (programa) de DescartesJS se pueden omitir. En cuanto a la instrucción Escribir, debemos usar el selector Gráficos y agregar el gráfico texto pero, ... mejor observa el vídeo:
Pudiste observar que usamos un texto para escribir la solución de nuestro problema: Promedio = [Prom]. En DescartesJS las variables deben ir encerradas entre corchetes para que se muestre el valor de dicha variable. Por ahora, hemos usado un texto simple, más adelante veremos el texto enriquecido de DescartesJS, que permite presentar expresiones más elegantes o, si se prefiere, más atractivas.
Problema 2. Se tienen los tres lados de un triángulo. Elabora un pseudocódigo y ejecútalo en DescartesJS para obtener el área del triángulo (usa un control de tipo campo de texto).
El área de un triángulo dados sus lados $a$, $b$ y $c$, según la fórmula de Herón, es $\sqrt{s(s - a)(s - b)(s - c)}$, donde $s$ es el semiperímetro del triángulo $(a + b + c)/2$. Observa el pseudocódigo para la solución de este problema:
InicioLeer a, b, cs = (a + b + c)/2Escribir AreaFinYa habíamos dicho que DescartesJS permite varias alternativas para resolver un problema, para este segundo problema usaremos dos alternativas, pero antes nos detendremos en la instrucción de entrada Leer, que en algunos lenguajes de programación se emplean palabras reservadas como input o read para ejecutar dicha instrucción.
En DescartesJS usaremos el control tipo campo de texto.
Veamos, entonces, cómo solucionamos el problema 2 con la herramienta DescartesJS.
E1, que aparece por defecto, le desactivamos los checkbox ejes, red y red10 con el fin de eliminar el plano cartesiano de nuestro objeto.texto con la siguiente configuración: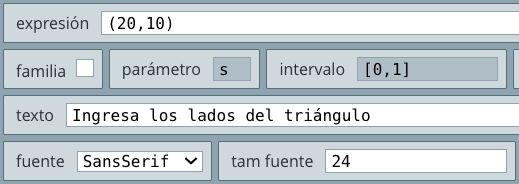
a del triángulo, para ello, en el selector Gráficos agregamos un gráfico texto, tal como lo muestra la siguiente imagen: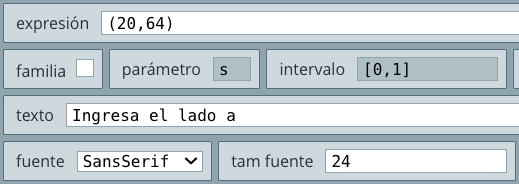
Realizamos el mismo procedimiento para los lados b y c (usa la opción copiar con el botón *) con las expresiones (20,124) y (20,184) respectivamente.
campo de texto (selector Controles), con la siguiente configuración: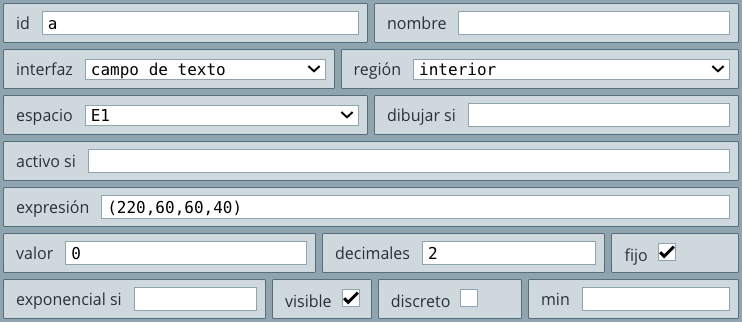
Igualmente para los otros dos controles con expresiones (220,120,60,40) y (220,180,60,40) respectivamente. Observa que el identificador de cada control (id) debe ser el nombre de la variable (a, b y c) que corresponde a los lados del triángulo, además de haber borrado el nombre del control.
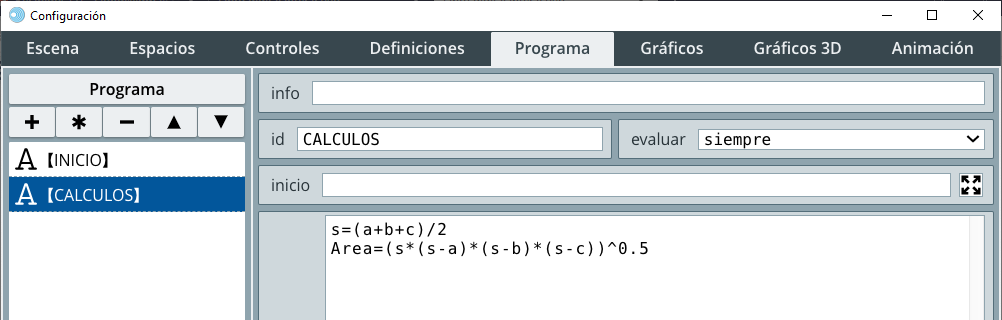
CALCULOS (selector Programa). Hemos seleccionado este algoritmo con evaluar siempre porque podemos cambiar los valores de los lados en cualquier momento (siempre) y obtener una nueva área del triángulo (observa la ).El cálculo de la raíz cuadrada se puede hacer elevando a 0.5 la expresión (s*(s - a)*(s - b)*(s - c)) o usando la función sqrt(x). Esta función la usaremos en la segunda alternativa.
texto con la siguiente configuración: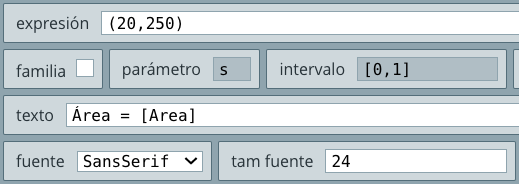
Puedes cambiar algunas propiedades, como el color y tamaño del texto.
Este es el objeto interactivo obtenido:
Prueba con el triángulo de lados $3$, $4$ y $5$, cuya área debe ser $6$. ¡Debes presionar la tecla Intro después de ingresar el último lado!
En la segunda alternativa vamos a usar dos controles tipo botón para que muestre el resultado, una vez hallamos ingresado los valores de los lados. Incluiremos, además, condicionales que activan o desactivan los campos de texto y los botones.
Cuando decimos que es una nueva alternativa es porque la estructura secuencial no la escribiremos en el selector Programa, sino en un parámetro del control botón. ¡Manos a la nueva obra!
campo de texto, es decir, en los controles para ingresar los lados a, b y c. Este condicional será muestra = 0 (ver la siguiente figura).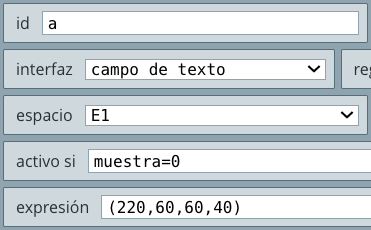
Esto significa que el campo de texto estará activo si la variable muestra es igual a cero. Por defecto, en DescartesJS todas las variables, no inicializadasEste término, ya aceptado por la academia de la lengua, significa establecer los valores iniciales de un programa. La mayoría de lenguajes de programación exigen que las variables a utilizar en un programa, sean inicializadas, que incluye valores y tipo de dato, por ejemplo, a = 0 de tipo real., tendrán un valor de cero. lo que significa que al ejecutar el objeto interactivo, los campos de texto estarán activos.
(20,300), ello para abrir una área donde irá nuestro botón (observa la siguiente figura).
Ya sabemos que te estás preguntando ¿qué ocurrió con el texto?, ¿qué es esa expresión extraña? La respuesta es que hemos usado texto enriquecido, el cual se activa haciendo clic en el botón  , que nos mostrará el editor de textos enriquecidos:
, que nos mostrará el editor de textos enriquecidos:

Hemos recurrido a este tipo de texto, porque el valor de una área debe estar en unidades cuadradas ($u^2$) y sólo con este tipo de texto es posible poner el exponente, usando el botón  ,
, expr debe contener el nombre de la variable Area. Bueno, por ahora, no has visto cuál es la alternativa, sólo habrás notado que estamos volviendo más elegante o, mejor dicho, más atractivo nuestro interactivo. ¡Vamos a ello!
botón con esta configuración: el nombre es Calcular Área en la región interior, expresión (125,250,150,30), colores a tu elección, tamaño de fuente en 22.Puedes observar que la alternativa existe porque el código del programa lo trasladamos a la acción calcular del control tipo botón. Observa, además, que una vez hacemos clic en el botón, a la variable muestra le asignamos el valor de 1, situación que inactiva los campos de texto y hace que aparezca el segundo botón. Dos novedades más: le pusimos imagen de fondo al interactivo y usamos la función raíz cuadrada proporcionada por DescartesJS: sqrt (SQuare RooT).
Este es el objeto interactivo obtenido:
Problema 3. Dado dos puntos aleatorios del plano cartesiano. Elabora un pseudocódigo y ejecútalo en DescartesJS para obtener la distancia entre los dos puntos.
He aquí el pseudocódigo
InicioEscribir Puntos y DistanciaFinUna vez te expliquemos cómo generar números aleatorios, estarás en capacidad de programar la solución del problema en DescartesJS, con lo que hemos trabajado en los problemas anteriores. Por ello, no nos detendremos en mucho detalle como lo hemos hecho antes. Por otra parte, no nos limitaremos sólo a generar los puntos, calcular su distancia y mostrar resultados, pues es una gran oportunidad de usar las ventajas que nos ofrece DescartesJS. Así que, resolveremos el problema y mostraremos su solución tanto numérica como gráfica.
id = E2) de ancho 30%, desactivando los checkbox: ejes, red, red10 y texto.id = E3) en x=30%, ancho=70% y escala=20. Activa el checkbox números.Existe solamente una variable general de DescartesJS, que es rnd. Esta variable, cuyo nombre viene de random (o aleatorio) genera un valor aleatorio real entre $0$ y $1$ cada vez que es llamadaEn realidad, se genera un número entre 0 y 0.999....
Si queremos generar números aleatorios entre $1$ y $20$, usamos rnd*20 + 1 o -(rnd*20 + 1) si queremos generarlos entre $-20$ y $0$. Sumamos 1 porque rnd*20 genera números entre $0$ y $19.999...$
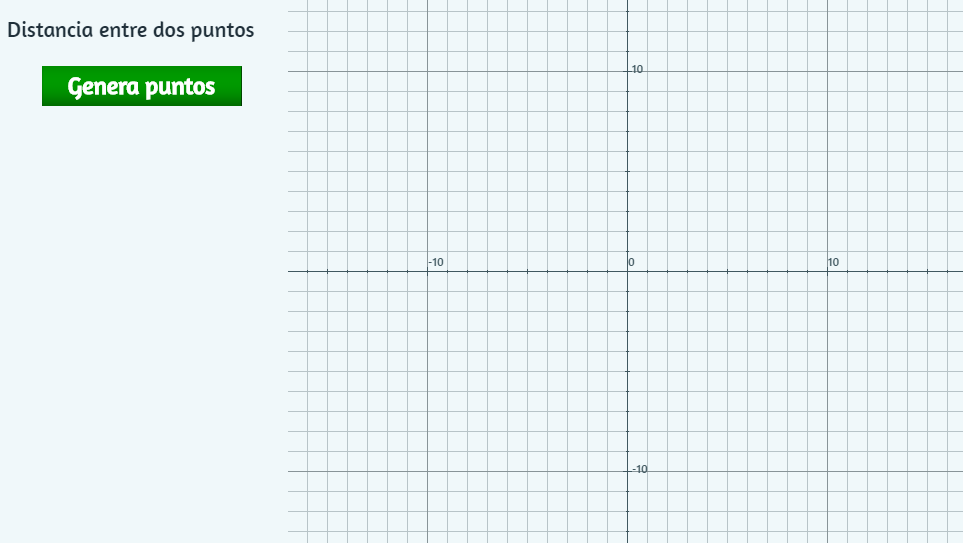
Continuemos, entonces, solucionando nuestro problema:
E2, escribe el título del problema Distancia entre dos puntos.E2, agrega un botón con nombre Genera puntos y activo si muestra=0, usa los colores y tamaño a tu gustoHasta aquí, debes tener un objeto como:
calcular y en parámetro, escribes: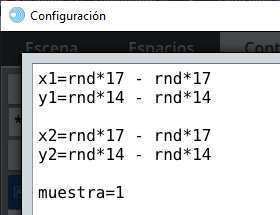
Observa que una vez se haga clic en el botón, suceden tres eventos. El primero es que se calculan las coordenadas de los dos puntos, si miras bien la gráfica del espacio E3, el eje $x$ muestra el intervalo [-17, 17] y el eje $y$ [-13, 13], por ello, hemos generado los números aleatorios entre esos valores; por ejemplo, para las abscisas con números aleatorios rnd*17 - rnd*17, que garantiza tanto números negativos como positivos. Es importante que comprendas que la expresión no se anula, pues cada uno de los términos genera un número diferente. El segundo evento es el que asigna 1 a la variable muestra. El tercero, consecuencia del anterior, es que se inactiva el botón.
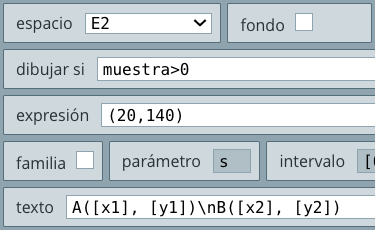
Observa que en el texto, las variables van encerradas entre corchetes. La expresión \n equivale a un salto de línea. Este texto aparecerá cuando el valor de la variable muestra es mayor que cero. Si analizas el resto del objeto interactivo, entenderás la expresión.
botón, ubicado más abajo del texto anterior, con la misma configuración del botón anterior, excepto por su posición, por la expresión en activo si, que ahora es muestra=1 y por el nombre que es: Halla distancia. No olvides seleccionar el espacio E2.calcular y en parámetros escribimos: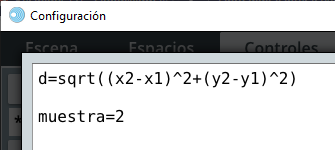
Distancia = [d] u, ubicado más abajo del botón anterior, que sólo se mostrará si muestra=2.Otro ejercicio, se mostrará si muestra=2 y en acción seleccionamos inicio, que tiene como función reiniciar el interactivo.Ya tenemos todos los elementos del espacio E2, nos falta incluir los elementos gráficos del espacio E3.
(x1,y1), que se mostrará solo si muestra>0. Se trata del punto $A$. Hemos elegido el color rojo y el tamaño del punto en 4. Similarmente, agregas el punto $B$. No olvides seleccionar espacio E3.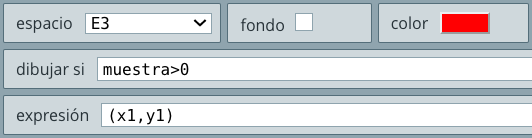
segmento cuya expresión es (x1,y1)(x2,y2), que corresponde a los puntos $A$ y $B$.Este es el objeto interactivo obtenido:
Observa que al hacer clic sobre el plano cartesiano se muestran las coordenadas del punto sobre el que haces clic. También, puedes desplazar el plano con clic izquierdo sostenido o hacer zoom con clic derecho sostenido.
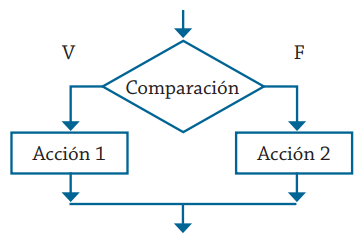
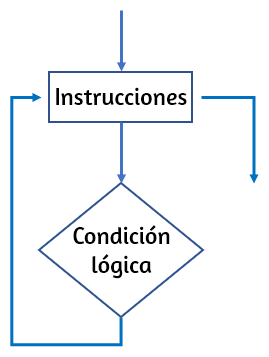
En los algoritmos, las estructuras selectivas o condicionadas son de la forma:
Si comparación verdadera
Entonces
Hacer acción 1
Sino
Hacer acción 2
Fin si
En un diagrama de flujo es, quizá, más fácil apreciar el proceso de selección en una estructura condicionada (observa la ).
En DescartesJS, la estructura anterior se escribe así: comparación?accion1:acción2, donde la comparación usa operadores booleanos.
Por otra parte, las acciones 1 y 2, generalmente, devuelven el valor a una variable (var), por lo que en general la estructura selectiva en DescarteJS sería de la forma: var = comparación?accion1:acción2. Los operadores booleanos en DescartesJS, los puedes consultar en este texto:
Problema 4. Dado dos números. Elabora un pseudocódigo y ejecútalo en DescartesJS para obtener el número mayor.
El pseudocódigo para este problema clásico, sería:
InicioLeer dos números A, BSi A>B
Entonces
Mayor=A
Sino
Mayor=B
Fin siEscribir número mayorFinEl objeto interactivo en DescartesJS, correspondiente a este pseudocódigo, excepto por la instrucción 3, ya lo sabes diseñar. Veamos cómo construyes el condicional.
Puedes usar el algoritmo CALCULOS del selector Programa o el parámetro de la acción calcular de un control tipo botón. Nosotros hemos usado la segunda alternativa, así:
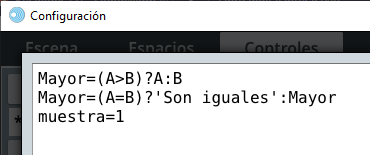
La primera línea Mayor=(A>B)?A:B, es fácil de comprender. Si la comparación es verdadera (A>B), el número mayor es A, sino es B. La segunda línea responde a la situación donde los dos números son iguales, asignando a la variable Mayor una cadena de caracteres: 'Son iguales', ¡Fácil! ¿No?
El objeto interactivo quedaría así:
Una novedad en este diseño es la reducción de decimales, tanto en los campos de texto como en el texto de respuesta, a cero cifras decimales.

Problema 5. Dado un número. Elabora un pseudocódigo y ejecútalo en DescartesJS para determinar si el número es de tres cifras (usa campo de texto).
Supondremos que el número es un entero. Así las cosas, el pseudocódigo es:
InicioLeer un número entero NSi (N > 99) y (N < 1000)
Entonces
Rta = "Es de tres cifras"
Sino
Rta = "No es de tres cifras"
Fin siEscribir respuesta (Rta)FinResuelve el problema 5 en DescartesJS. Ten en cuenta que la comparación del Si se escribe así: (N > 99)&(N < 1000).
Problema 6. En un almacén se tiene la siguiente promoción: todo artículo con un precio superior a $\$25,000$ tendrá un descuento del $20\%$, los demás tendrán el $10\%$. Elabora un pseudocódigo y ejecútalo en DescartesJS para determinar el precio final que debe pagar una persona por comprar un artículo y el valor del descuento.
Otro problema sencillo que puedes resolver, sólo recuerda que si el artículo vale $\$30,000$, el descuento será: 30000*20/100.
Resuelve el problema 6 en DescartesJS.
Problema 7. Se tiene el nombre y la edad de tres personas. Se desea saber el nombre de la persona de mayor edad. Elabora el algoritmo correspondiente y ejecútalo en DescartesJS.
Para este caso, una alternativa es usar estructuras selectivas anidadas; sin embargo, para este nivel, hemos optado por un pseudocódigo simple como el siguiente:
InicioLeer los nombres N1, N2 y N3Leer las edades Ed1, Ed2 y Ed3Si (Ed1 > Ed2) y (Ed1 > Ed3)
Entonces
PersonaMayor = N1
Sino
PersonaMayor = PersonaMayor
Fin siSi (Ed2 > Ed1) y (Ed2 > Ed3)
Entonces
PersonaMayor = N2
Sino
PersonaMayor = PersonaMayor
Fin sicontinua en la siguiente página.
Si (Ed3 > Ed1) y (Ed3 > Ed2)
Entonces
PersonaMayor = N3
Sino
PersonaMayor = PersonaMayor
Fin siEscribir el nombre de la persona mayorFinSi haces un análisis del comportamiento del algoritmo, te darás cuenta que siempre encontrará el nombre de la persona mayor. Obviamente, partimos del supuesto de edades diferentes.
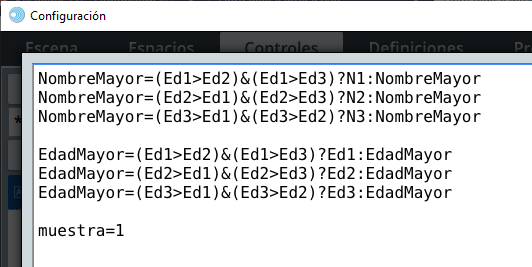
El problema original también pide la edad de la persona mayor, lo cual se puede hacer con tres instrucciones similares a las anteriores, pero cambiando la acción del Si verdadero por EdadMayor = N1, N2 o N3, según la comparación correspondiente.
En DescartesJS el algoritmo, para las dos preguntas, sería así:
Aprovechamos la solución de este problema, para abordar, de nuevo, el gráfico texto. Habíamos visto que los controles y los textos se posicionan en un espacio 2D de acuerdo a unas coordenadas (expresión), que se miden a partir de la esquina superior izquierda del espacio. Además, que la ordenada es positiva de arriba hacia abajo, contrario a como funciona el plano cartesiano, estas coordenadas, así establecidas, se llaman coordenadas absolutas. No obstante, DescartesJS permite el uso de coordenadas relativas, que funcionan de acuerdo al plano cartesiano. Usaremos esta propiedad para el diseño de la solución de nuestro problema.
En primer lugar, crea un objeto interactivo (Archivo → Nuevo) con dimensiones $600\times 500$ pixeles (selector Escena). A continuación, crea un texto (selector Gráficos), tal como aparece en la .

En la puedes observar que hemos desactivado el checkbox de coord abs (coordenadas absolutas), lo que quiere decir que hemos activado las relativas. En el objeto que has creado, escribe el texto Hallar la persona de más edad en la posición (0,0) ¿qué ocurre? Luego, modifica el punto de anclaje, ¿qué concluyes? Observa la , en la cual aparecen varias opciones y, finalmente, el texto centrado en las coordenadas (0,5) con punto de anclaje arriba-centro.
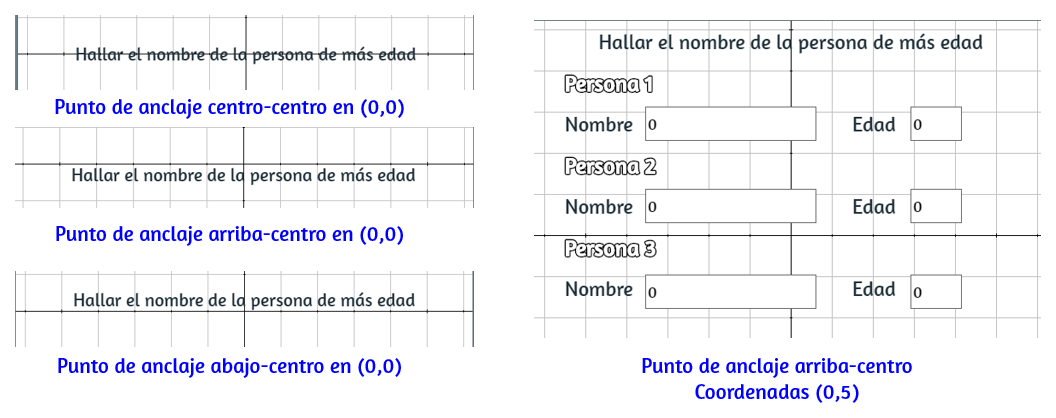
Ahora el texto lo posicionamos en el espacio de acuerdo a las coordenadas cartesianas, los demás textos de la se diseñaron usando estas coordenadas, lo cual nos lleva a concluir que no debemos desactivar el plano cartesiano, hasta no terminar nuestro diseño.
El objeto interactivo, finalmente diseñado, nos ha quedado así:
El efecto especial en el título y otros textos se logra activando el checkbox borde texto.
Puedes ingresar los datos usando la tecla de tabulación para cambiar entre los campos de texto y al final presiona la tecla intro, para activar el botón Calcular. Trata de obtener este objeto interactivo con lo que has aprendido.
Una estructura iterativa o de repetición es aquella que permite que un proceso o conjunto de acciones se realice de manera cíclica (loop o bucle). Este proceso repetitivo se realiza mientras una condición lógica sea verdadera. Existen cuatro formas comunes de este tipo de estructuras: "Hacer mientras" (Do-While), "Mientras que", "Repite hasta que" y "Desde, hasta" (For-next). En este apartado sólo trabajaremos con la primera forma, pues es la que usa DescartesJS. En la se presenta la forma Do-While en un diagrama de flujo.
Problema 8. Elabora un pseudocódigo y ejecútalo en DescartesJS para calcular la suma de los $100$ primeros números naturales (no uses la fórmula directa).
El pseudocódigo para resolver este problema, es el siguiente:
Inicioc ← 0S ← 0Hacer
c ← c + 1
S ← S + c
Mientras c < 100
Fin HacerEscribir SFinHemos usado el carácter ← para recordar la instrucción tipo asignación. Si bien DescartesJS inicializa las variables no declaradas en cero, las hemos declarado, sólo para observar cómo se puede hacer en una estructura Hacer-Mientras de DescartesJS que, para este problema, se muestra en la siguiente figura:
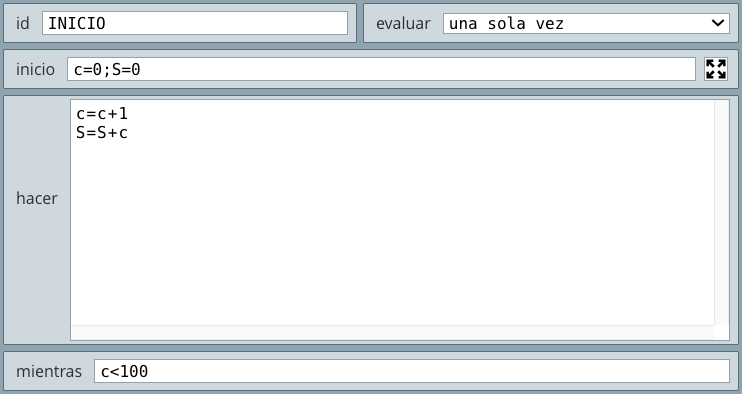
Hemos usado el algoritmo INICIO del selector Programa, del cual explicamos:
inicio, inicializamos las variables c y S en cero (cada instrucción separada por un punto y coma). Estas variables corresponden a un contador de números (c) y a la suma de esos números (S).hacer escribimos las acciones a repetir. La primera es c = c + 1, que tiene como función contar números así: c = 0 + 1, c = 1 + 1, c = 2 + 1, ... que asigna a c los números 1, 2, 3, ... La segunda tienen como función sumar esos números así: S = 0 + 1, S = 1 + 2, S = 3 + 3, ..., es decir, suma a S los números naturales desde 1 hasta 100 (el número que hace la condición falsa).mientras ponemos la condición c<100.Sólo nos resta escribir S, que en DescartesJS lo logramos con el gráfico texto del selector Gráficos, así:

Al ejecutar (Aplicar) el objeto interactivo, nos aparece los siguiente:

Problema 9. En un archivo se tienen los datos de la estatura de un grupo de $15$ estudiantes. Elabora un pseudocódigo y ejecútalo en DescartesJS para calcular la estatura promedio (usa un vector de estaturas).
El pseudocódigo que soluciona este problema es el siguiente:
Inicioi = 0S = 0Hacer
i = i + 1
Leer Estatura
S = S + Estatura
Mientras i < 15
Fin HacerEscribir S/15FinEn DescartesJS creamos el interactivo así:
Antes de explicar el algoritmo usado por DescartesJS, te recomendamos leer el siguiente texto:
Tal como lo observaste en el vídeo o lo consultaste en el texto, una forma de evitar el ingreso o lectura de $15$ variables es el uso de vectores. En este caso, desde el selector Definiciones, agregamos un vector identificado como E. A cada elemento E[i] del vector E le asignamos una estatura. Quizá se nos olvidó definir el tamaño del vector, que tendría que ser 16, pues el elemento E[0] también cuenta, este olvido no impidió que el interactivo funcionara, pero es más correcto dimensionar el vector.
A continuación, desarrollamos el código de nuestro problema usando el algoritmo INICIO en el selector Programa. Las variables que usamos fueron un contador i y S para calcular la suma de las edades. En el caso de S, observa que le sumamos los elementos del vector E, así:
S e i se inicializan en cero.i = i + 1, a i se le asigna el valor de 0 + 1, o sea 1.S = S + E[i] que, en este paso, equivale a S = S + E[1] o, de acuerdo a los valores de los elementos del vector, S = S + 1.45i < 15, que en este momento es verdadera, por lo que se repite el proceso, hasta que la condición sea falsa, es decir, hasta que i sea igual a 15, lo que garantiza que se sumen las 15 estaturas.15.Problema 10. Se requiere un algoritmo para determinar, de N cantidades, cuántas son menores o iguales a cero y cuántas mayores a cero. Realiza el pseudocódigo y ejecútalo en DescartesJS para resolver el problema.
Bueno... esa es la tercera parte de la tarea 3.
Al terminar este capítulo, habrás desarrollado la siguiente actividad:
En el selector Controles puedes encontrar diez tipos de control. Para este capítulo, sólo trabajaremos cinco de ellos, pues ya los hemos hecho con los controles tipo botón y campo de texto. Los controles de Audio y Vídeo los veremos más adelante.
Iniciamos nuestra primera parte de la actividad planteada al inicio de este capítulo, usando el control pulsador.
control1.html.50. Esto tendrá efecto cuando el control se posiciona en el norte o sur de la escena, como veremos a continuación.
pulsador, con la siguiente configuración: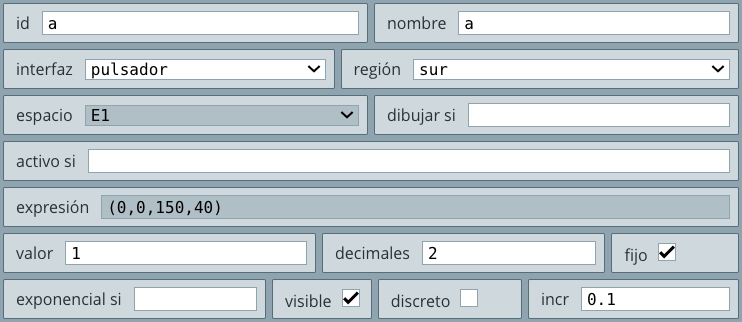
Observa que se deja en la región sur, su id es la letra a y tiene un valor inicial de 1.
id) y nombrados como b y c. Estos controles tienen la misma configuración del primero.ecuación con la expresión y=a*x^2+b*x+c, en el cual puedes elegir otro color y con ancho igual a 2, este es el interactivo que obtendrías:Usa los controles para observar su efecto en la gráfica, el cual se logra al incluir los id en la ecuación cuadrática. Por ejemplo, cambia el valor de a a un número negativo. ¿Qué ocurre al cambiar el valor de c?
Continuamos con la segunda parte de la actividad planteada al inicio de este capítulo, usando el control barra.
control2.html.50.barra, con la siguiente configuración: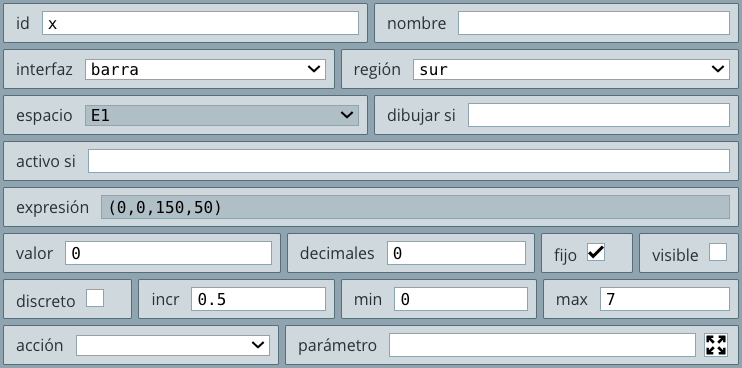
Observa que se deja en la región sur, su id es la la letra x y tiene un valor inicial de 0. Por otra parte, hemos definido sus límites mínimo y máximo en 0 y 7 respectivamente.
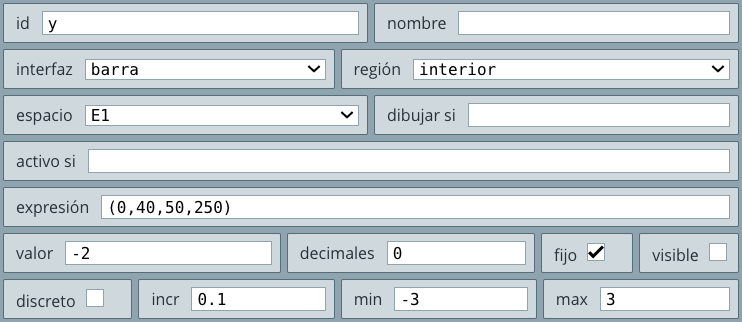
Observa que, como lo dice el texto introductorio, hemos creado una barra vertical, al cambiar la región por interior e invertir los valores del ancho y el alto a 50 y 150 respectivamente. Otros cambios están en el id que es la la letra y con un valor inicial de -2. Los límites mínimo y máximo en -3 y 3 respectivamente. A continuación entenderás el por qué de estos valores.
imagen (la que tu quieras), de tal forma que su tamaño sea el adecuado, es decir, debes usar un ancho y un alto de imagen que permita su visionado en la escena. Nosotros hemos usado 0.9 para ambos valores de la escala de la imagen:
Observa que la posición de la imagen es (x,y), variables que dependen de los controles tipo barra agregados inicialmente. Recuerda definir bien la ruta donde se encuentra tu imagen, en nuestros caso es:

Este es el interactivo obtenido:
Seguimos con la tercera parte de la actividad planteada al inicio de este capítulo, usando el control Casilla de verificación.
control3.html.casilla de verificación, con la siguiente configuración: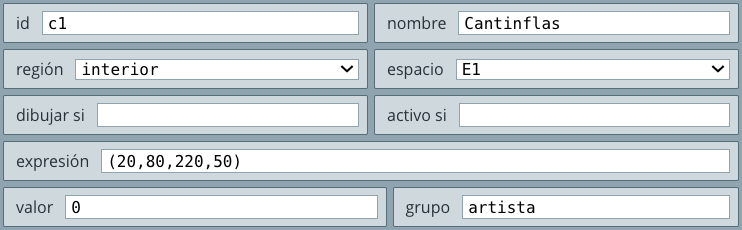
Observa que en el campo de texto grupo hemos puesto la palabra artista, esto con el fin de asignar la misma palabra a dos controles más que vamos a agregar y, así, definir las casillas de tipo radio botones. La posición de la casilla la hemos definido en (20,80) y con unas dimensiones de $220\times 50$, todo esto lo observas en la opción expresión, el nombre del control es cantinflas.
Juanes y Salma Hayek, con expresiones (20,140,220,50) y (20,200,220,50) respectivamente. Habrás notado que los identificadores de los tres controles creados son c1, c2 y c3.textos (selector Gráficos) para terminar esta parte de la actividad.El primer texto es la pregunta, que pondremos centrada y..., mejor observa el vídeo:
Es importante que comprendas la expresión booleana empleada para mostrar el tercer texto, la cual es la disyunción (c1=1)|(c3=1), que permite mostrar el texto ¡No es correcto!, cuando se activan la casilla 1 (c1) o (|) la casilla 3 (c3).
Nuestra cuarta parte de la actividad de este capítulo, consiste en una imagen que podemos desplazar con clic sostenido. El control gráfico es el que nos permitirá hacerlo, para ello... pues... observa:
Lo del control gráfico, muy simple. Lo del texto centrado, tiene mayor configuración, ¿recuerdas lo de \n?, pues indica un salto de línea, así pudimos centrar mejor el título.
Seguro te preguntarás ¿qué pasó con el gif animado? Recuerda que en DescartesJS no funciona, tendríamos que usar un espacio HTMLIframe y... ese va a ser nuestro próximo reto ¡Desplazar un espacio con clic izquierdo sostenido!, presta atención.
HTMLIframe con ancho y alto igual a las dimensiones de tu gif. Nosotros hemos elegido el caballo de los estudios fotográficos de Eadweard Muybridge, que mostramos en el capítulo III, cuyas dimensiones son $220\times 16$. 
2D el cual debe tener esta configuración: plano cartesiano desactivado, color transparente (para que se vea el gif) y escala = 1 ¡Ojo con la escala... es 1! Este nuevo espacio te aparecerá con un id = E3, déjalo así.control gráfico, cuya imagen es el gif animado ¡Debes estar en el espacio E3! Si has seguido bien el procedimiento, debes tener esta escena:¡Claro que tu escena está más grande! Observa que el gif animado tapa parte del título, ello por que no tiene transparencia... continuemos:
control gráfico (caballo estático), en las coordenadas (0,0). El segundo, es el espacio HTMLIframe (caballo dinámico) cuyo marco de referencia es a partir de la esquina superior izquierda, coordenadas (0,0). Recuerda que su diferencia principal es que el primero tiene el eje $y$ positivo hacia arriba, mientras que el segundo lo tiene hacia abajo. Entender esta diferencia, posibilita que podamos sincronizar las dos imágenes, es decir, que estén en la misma posición... veamos:500, por lo tanto, el caballo estático se encuentra a 250 pixeles del eje $y$ del segundo sistema de referencia (esquina superior izquierda), lo que significa que el caballo dinámico lo debemos desplazar 250 menos su ancho: 250 - 110. Pero, como vamos a mover el control gráfico, debemos sumarle el valor, en $x$, de ese desplazamiento, es decir: g1.x + (250 - 110)450 y el alto de la imagen 165. Con un análisis similar, debemos realizar la siguiente resta: 225 - 82.5. dada la diferencia en el eje $y$ de los dos sistemas, debemos desplazar hacia abajo el caballo dinámico, de la siguiente manera: -(g1.y - (225 - 82.5)) ¿cómo fue eso?... bueno, ya es momento que pienses un poco, ¡analízalo!HTMLIframe y cambia los valores de x y y por los que acabamos de analizar:
control gráfico (sin transparencia) quedó sobrepuesto al gif animado, que era nuestro propósito inmediato, más no el propósito inicial ¿qué hacer? Si regresas al control gráfico, observarás que al igual que muchos objetos del editor de configuraciones, tiene el campo de texto dibujar si, pues bien, pongamos una expresión falsa, por ejemplo: Medellin>Nacional, obviamente falsa. Si no te gustó esa expresión, puede ser esta 1=2, también falsa. De esa manera ocultamos la imagen del control, mas no la acción del control. ¿Cómo así?, pues observa el resultado final:Ahora tendrás una idea de cómo diseñamos el memoriza de imágenes animadas presentado en el capítulo III.
Ya te estás imaginando cuál es la tarea, ¡Terminar la actividad planteada al inicio del capítulo!
Te damos un empujón:
2D con ancho del 30% o, si prefieres, un ancho de 225, en este espacio pondrás el control tipo menú.HTMLIframe con un ancho del 70% y ubicado en x = 30%, en el campo de texto archivo, escribes [file]INICIO, escribes:file='control1.html'
tipo='Pulsador'
Si analizas, podrás concluir que el html que se mostrará en el espacio HTMLIframe es la primera parte de la actividad que desarrollamos (control1.html) y te da una pista para usar adecuadamente el control menú; por ejemplo, cuando la opción del menú sea Barra, éste debe calcular, algo así como:
file=(m1=1)?'control2.html':file
Recuerda que este condicional se interpreta así: Si (m1=1) es verdadero, la variable file es igual a 'control2.html', sino sigue manteniendo el mismo valor.
En este caso, m1 es el id del menú. Algo similar debes hacer con la variable tipo.
tipo, Control\n[tipo].Demasiada ayuda... Termina la tarea.
Al terminar este capítulo, habrás desarrollado la siguiente actividad:
Formatos de audio. Existen varios formatos de audio que resumimos así:
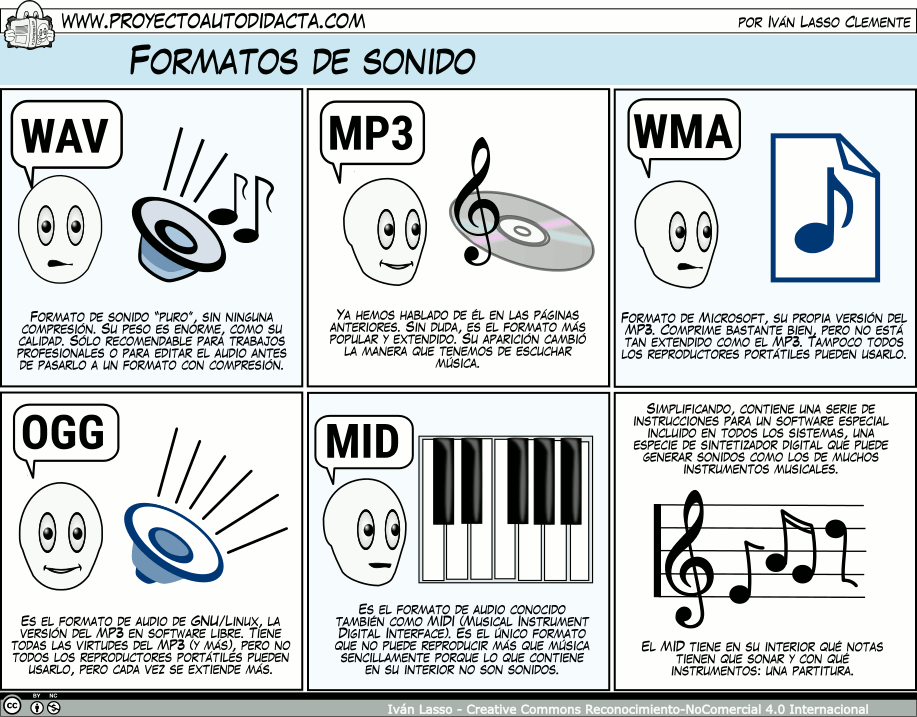
DescartesJS acepta archivos en formato mp3, ogg, oga y wav, aunque se recomienda el uso del formato mp3 para que los audios funcionen en todos los navegadores, las funciones asociadas a estos archivos se describen en el siguiente texto:
Un ejemplo de uso del control tipo audio, es el siguiente:
Veamos cómo se diseñó la escena anterior:
E1, el que aparece por defecto, desactivamos el plano cartesiano.menú con id=s, expresión (10,80,150,40), región interior y las siguientes opciones:
2D con la siguiente configuración:
En este espacio aparecerán las imágenes del interactivo
De acuerdo a las opciones del control tipo menú, hemos descargado siete audios en formato mp3, correspondientes a dichos animales. Existen varias páginas que ofrecen descargas gratis de este tipo de archivos, nosotros los hemos descargado de la siguiente página: http://sonidosmp3gratis.com/animales
audio; por ejemplo, el primero lo hicimos así (en el selector Controles):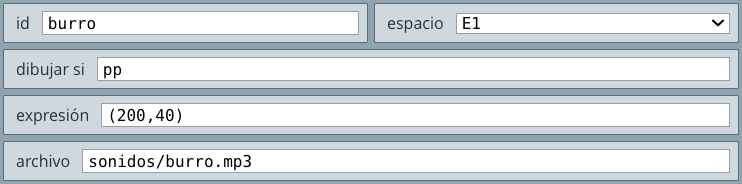
id que le asignes a cada audio, pues debe ser el mismo que uses en las funciones de audio.vector con id=I (selector Definiciones), cuyos elementos serán las direcciones relativas a estas imágenes (encerradas entre comillas simples).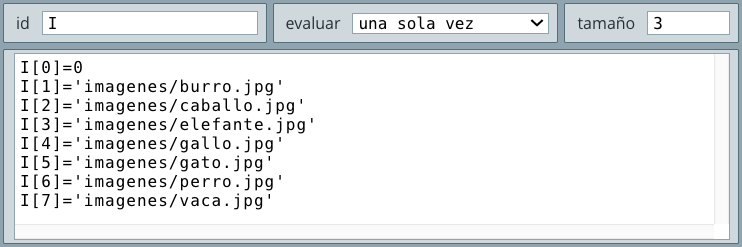
E2, expresión (0,0) y archivo [I[s]]. No olvides lo del espacio. Observa que en archivo hemos puesto el elemento I[s] del vector I, donde s corresponde a la opción que se seleccione del control tipo Menú; por ejemplo, si seleccionas Gato corresponde al elemento I[5] del vector I; es decir, imagenes/gato.jpg, que será la imagen que se mostrará en E2. Puedes probarlo en este momento.Menú y en acción selecciona calcular, con los siguientes parámetros: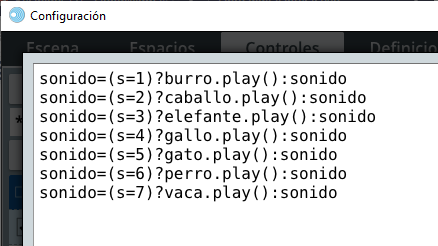
La variable sonido, en realidad no se le asigna ningún valor, por ello, se le suele llamar variable muda. Lee el siguiente texto.
Así las cosas, el audio del gato se activaría con el condicional:
sonido=(s=5)?gato.play():sonido,
lo que significa que cuando seleccionas la opción Gato en el menú, la expresión s=5 es verdadera, por lo tanto, se ejecuta la función gato.play(). Recuerda que las opciones del menú inician en cero, por ello Gato es la opción cinco. Recuerda, también, en hacer coincidir el id del audio con el del condicional, que en este caso está escrito en minúsculas.
Habrás notado que en la configuración del audio hemos puesto en dibujar si, la expresión pp. Esta expresión equivale a pp=1 que, para nuestros propósitos, es ocultar los controles de audio, en tanto que pp=1 es una expresión falsa. Finalmente, sólo falta escribir el título, lo cual ya sabes hacer.
Formatos de vídeo. Existe una gran variedad de formatos de vídeo, que pueden ser usados para la web o para otros propósitos que requieren mayor calidad; por ejemplo, películas HD o 4K. Algunos de esos formatos son los siguientes:
En DescartesJS contamos con el control tipo vídeo, que acepta los formatos HTML5:
Así las cosas, para las actividades que vamos a desarrollar (previas a la del inicio de capítulo), tienes que tener un vídeo compatible con HTML5, preferiblemente en formato mp4.
Tienes tres opciones. La primera es crear tus propios vídeos, la más recomendable. La segunda es descargarlos de algún repositorio de descarga libre; por ejemplo, de https://pixabay.com/es/videos/, hemos descargado este vídeo que muestra imágenes de Ecuador:
La tercera opción es enlazar el vídeo, la cual no tiene problemas con derechos de autor, pues estás haciendo uso del código embebido que ofrece el autor, a través de un servicio público de vídeos. Observa la primera actividad del siguiente apartado, la cual utiliza la tercera opción.
En este apartado veremos algunos objetos interactivos que incluyen vídeos, los cuales se incorporan utilizando el control tipo Vídeo.
Vídeos enlazados desde la web. En esta actividad, desarrollaremos el siguiente objeto interactivo:
No nos detendremos en mayores detalles, pues ya sabes cómo configurar textos y algunos controles. Por ello, sólo nos detendremos en aspectos relacionados con los vídeos y configuraciones especiales.
E1, de dimensiones $400\times 240$ y ubicado en x=250 y en y=110, tiene una imagen de fondo y sólo se muestra cuando la variable video es igual a cero (video=0).botón, similares a los que trabajamos en el apartado 3.3. El botón con flecha derecha tendrá los siguientes parámetros (no olvides activar antes la acción calcular):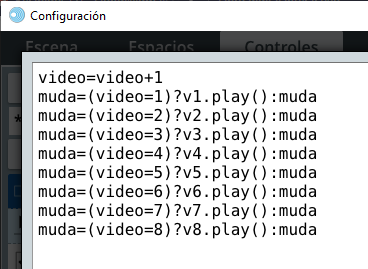
play()) un vídeo, según el valor de la variable video. El botón de la izquierda tiene los mismos parámetros, excepto por el primero, que sería video=video-1.(250,60,400,300), que se muestra de acuerdo al valor de la variable video.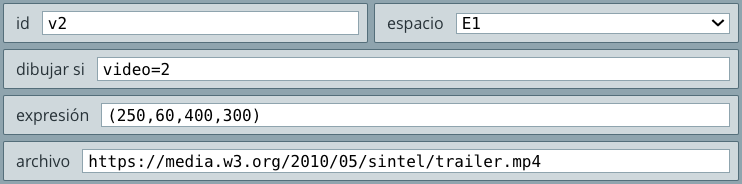
Observa que en archivo, hemos escrito el enlace. Puedes desarrollar la actividad con otros enlaces que hayas consultado. Si optas por los de este interactivo, hemos puesto una caja de texto para que los puedas copiar... a propósito de la caja de texto:
texto, con esta configuración: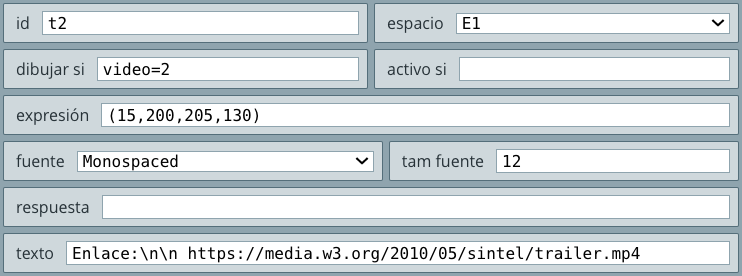
Las dos imágenes anteriores corresponden al segundo vídeo, similar configuración tienen los otros siete vídeos y cajas de texto.
Ya sólo resta agregar títulos y mensajes, los cuales se quedan de tarea.
Pero, antes de la tarea, te mostramos cómo escribimos los textos al lado izquierdo de la escena:
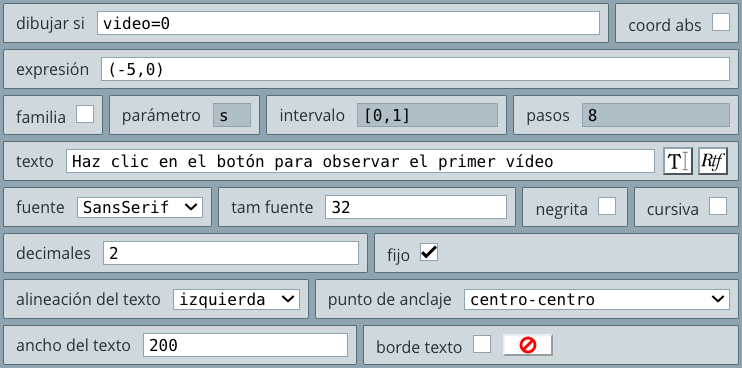
Es un texto en coordenadas relativas (-5,0). Lo novedoso es que lo restringimos a un ancho determinado, para este caso ancho del texto = 200. Para el caso de la figura anterior, es el texto que aparece al inicio del interactivo.
Termina esta actividad, de tal forma que se muestren sólo tres vídeos, uno por cada formato (MP4, WebM y OGV). Por cada vídeo debe aparecer el título del vídeo; por ejemplo, Trailer Toy Story. En la caja de texto, una brevísima descripción del vídeo.
La desventaja que tienen los vídeos enlazados es su dependencia con la conectividad; por ello, en este libro, procuramos que todos los vídeos estén en local, de tal forma que se pueda descargar el libro y leerlo sin conexión a Internet. Nuestra segunda actividad la realizaremos con un vídeo descargado.
Vídeos en local. En esta actividad, desarrollaremos el siguiente objeto interactivo:
videos.El propósito del objeto interactivo es ver una porción del vídeo, para lo cual usaremos las tres funciones de vídeo y la variable <identificador del control>.currentTime, definidas anteriormente.
E1 desactivamos el plano cartesiano.E2) en x=200, y=90, de dimensiones $430\times 320$ y fondo transparente. El objetivo de este espacio es impedir la manipulación de los controles del vídeo (Recuerda darle transparencia a este espacio).video en el selector Controles, así: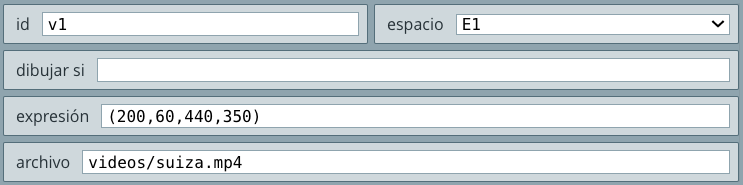
Obviamente, ya has descargado este vídeo y guardado en la carpeta videos. Si haces clic en aplicar, podrás verificarlo. Para que aparezca un poster o imagen previa copia, en esta carpeta, una imagen en formato png con el mismo nombre del vídeo, es decir, suiza.png.
menú con expresión: (10,90,180,40), opciones = Selecciona,Ginebra,Lucerna,Berna. Activamos la acción calcular e incluimos los siguientes parámetros: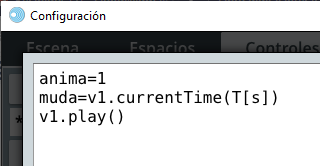
Son tres instrucciones que hacen lo siguiente:
anima=1 permite activar una animación, la cual explicamos más adelante;muda=v1.currentTime(T[s]), posiciona el vídeo en el segundo definido por el elemento T[s] del vector T;v1.play() envía la orden de reproducción del vídeo, a partir del segundo T[s]. A continuación definimos el vector T.ciudad, el cual almacena los nombres de las ciudades: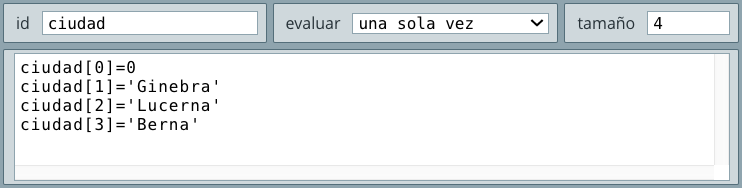
T, el cual almacena los tiempos de inicio de cada ciudad. Aquí es importante que, previamente, hayas tomado nota del tiempo transcurrido antes de iniciar una nueva ciudad; por ejemplo, la ciudad de Berna aparece en el segundo 43: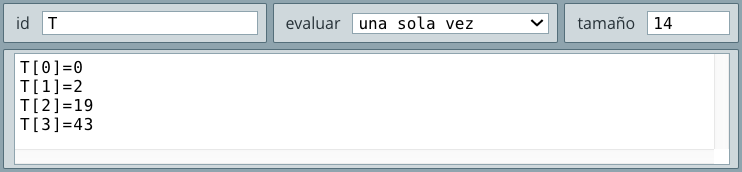
CALCULOS del selector Programa, escribimos estas instrucciones: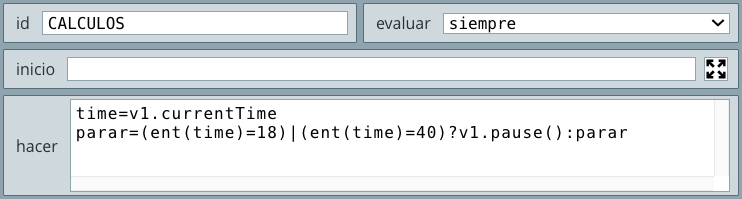
La primera instrucción permite obtener el tiempo transcurrido del vídeo, que se almacena en la variable time; para que funcione eficientemente, es necesario activar una animación... cualquier animación. La segunda instrucción compara el tiempo transcurrido (time) con los segundos 18 y 40, si la comparación es verdadera, se pausa el vídeo.
evento en el selector Programa:
Seguramente, te estarás preguntando que es un evento, pues...
En nuestro caso, este evento ejecuta la animación necesaria para que la variable v1.currentTime funcione eficientemente.
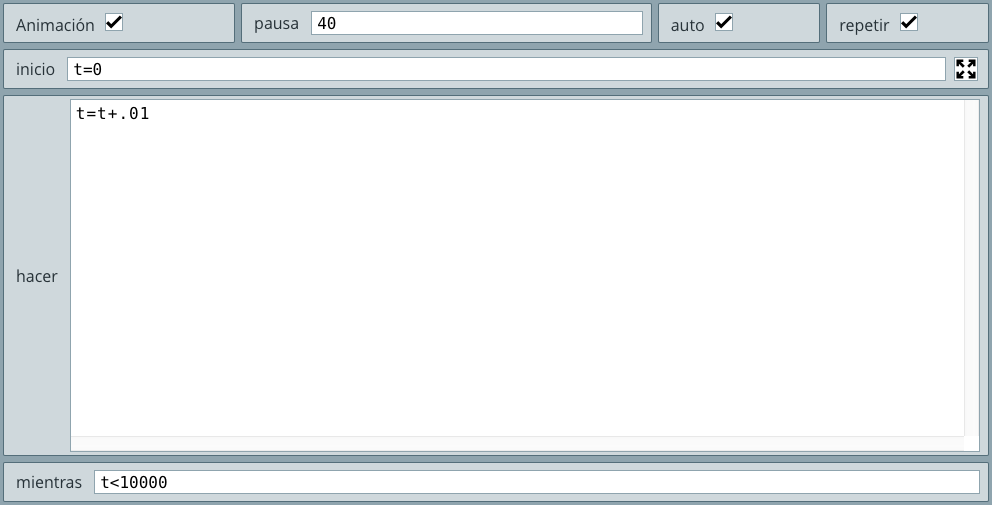
Nuestra última actividad es diseñar un vídeo interactivo, utilizando la variable y funciones de vídeo anteriores, pero antes es necesario que comprendas la importancia de un vídeo interactivo.
Los recursos digitales puestos al servicio de la educación, día a día crecen en cantidad y calidad. Además de la gran diversidad de repositorios, cuyo propósito es almacenar y disponer para el acceso libre de contenidos académicos como los resultados de investigación y las tesis de maestría o doctorado, existen otros recursos diseñados como herramientas de apoyo a los procesos de enseñanza y aprendizaje. Estos recursos, generalmente, se disponen en otros repositorios denominados bancos de objetos de aprendizaje, como lo es Agrega en España, objetos UNAM en México o el portal Colombia aprende.
El diseño o desarrollo de estos objetos de aprendizaje puede ser simple o complejo. Podríamos considerar de diseño simple, todos aquellos objetos que se obtienen de herramientas de fácil uso como un presentador de diapositivas o un editor de textos, que no puede dejar como inferencia que el contenido sea simple, pues el autor del objeto plasma allí toda una conceptualización en torno al objeto que se representa incluyendo, en algunos casos, una intencionalidad didáctica. Otros objetos demandan conocimientos expertos en el uso de herramientas más complejas, las cuales permiten el desarrollo, a su vez, de objetos de mayor complejidad como las animaciones o los objetos interactivos, tal es el caso del Flash de Adobe o los applets de JavaUna buena cantidad de recursos digitales han sido diseñados en Flash o en Java, con la consecuencia ya conocida de su incompatibilidad con dispositivos móviles..
En un estado intermedio se encuentran las denominadas herramientas de autor, tanto comerciales como de uso libre, entre ellas están GeoGebra, Cabri (comercial), Ardora, Lim, JClic y DescartesJS. Para el diseño de un objeto de aprendizaje con este tipo de herramientas, dependiendo de la cantidad de atributos inherentes al objeto, es posible que sean necesarios otros objetos como imágenes, textos, gráficos o vídeos.
El diseño de vídeos presenta una diversidad de formatos y tiempos de reproducción, la mayoría sin ninguna intencionalidad didáctica. Esta situación ha motivado el desarrollo de la propuesta que se comparte en este apartado, que permita al usuario, generalmente docentes, la creación de vídeos interactivos.
Cualquier vídeo que tenga una intencionalidad didáctica, en principio, podemos afirmar que es útil como herramienta de apoyo a los procesos de enseñanza y aprendizaje; no obstante, su impacto en estos procesos depende de algunos factores que discutiremos a continuación.
Todo vídeo facilita algunas acciones interactivas como el pausado y la reproducción en cualquier momento de la línea de tiempo del vídeo. Estas acciones permiten el acercamiento al objeto de conocimiento representado al ritmo del usuario que, en últimas, es un sujeto cognoscente o, si se prefiere, un estudiante que hace uso de este tipo de recurso.
No podemos ignorar que todo material educativo presenta niveles de consulta que depende de algunos factores condicionantes o, mejor aún, motivantes para ser consultados. El estudiante autodidacta o el usuario con claros intereses de acercarse a un objeto de conocimiento, es un potencial usuario de estos materiales, entre ellos los vídeos, sin importar la calidad o duración del mismo, pues su propósito es encontrar respuestas a algunos interrogantes surgidos en el proceso de construcción o reconstrucción del conocimiento. Si su propósito es conocer lo ocurrido en un evento de $1978$, es tan útil un vídeo en alta definición, como el producido con la tecnología de hace $40$ años. Sin embargo, tampoco podemos ignorar que en la época actual, en la que prolifera la información de fácil acceso, no es fácil motivar a los usuarios en general, y a los estudiantes en particular, para que usen o consulten los materiales educativos puestos a su disposición, lo que constituye un reto para los creadores de este tipo de recursos. Este reto es posible asumirlo, si se recurren a algunas estrategias que hagan el vídeo más atractivo o, en otras palabras, que el vídeo este diseñado de tal forma que atrape al usuario.
Ejemplos de vídeos con esta connotación especial proliferan en las redes sociales, los cuales son denominados “vídeos virales”, que presentan millones de reproducciones, los cuales se caracterizan por ser vídeos cortos con un contenido no intencional, generalmente casual, como el bebé que muerde el dedo de su hermanito o situaciones graciosas como las recopilaciones de caídas de personas en situaciones absurdas. Una primera conclusión, para acercarnos al tipo de vídeo atrapante es su duración, es decir, los vídeos deben ser cortos.
En una primera clasificación, podemos decir que existe una gran variedad de vídeos, que van desde las películas y documentales, hasta los simples vídeos caseros. Pero, para nuestro propósito, clasificaremos los vídeos en el ámbito educativo, los cuales presentan diferentes formatos y estrategias que permitan atrapar al usuario del vídeo.
En otras situaciones, donde la explicación en una pizarra es trascendental (matemáticas, física, estadística, etcétera), la presencia del profesor constituye en un distractor innecesario, pues se busca que el usuario o estudiante se concentre en las explicaciones sobre el objeto de conocimiento.
Partiendo de esta segunda conclusión (vídeos sin profesor), podemos encontrar varios tipos de vídeos posibles, que se obtienen con software capturador de pantalla, sea éste comercial como el Camtasia, o gratuito como el CamstudioExisten varias aplicaciones gratuitas que permiten crear vídeos capturando las acciones que realizamos en un ordenados, algunos son: Camstudio, Hypercam, Ezvid, Freeseer y Wink.:
Como lo enunciamos al principio, todo vídeo es útil como herramienta en los procesos de enseñanza y aprendizaje; sin embargo, es su impacto el que cuestionamos en este apartado. Los tipos de vídeo anteriores, tienen como deficiencia principal su unidireccionalidad, pues el sujeto que lo “ve” es pasivo. Nuestro propósito es el diseño de recursos digitales interactivos, en los que el sujeto es activo, en tanto que puede intervenir los atributos del objeto representado, en este caso el vídeo.
Se trata, entonces, de diseñar objetos interventivos, es decir, objetos con los cuales se interactúa.
Los vídeos interactivos, normalmente, son vídeos a los que se le agregan capas transparentes, con el fin de sobreponer elementos externos como imágenes, textos complementarios, cuestionarios y actividades interactivas. Actualmente se vienen desarrollando varias aplicaciones que permiten el diseño de este tipo de vídeos, por ejemplo, h5p. Es mucha la creatividad que se está generando con este tipo de vídeos, a tal punto que los premios Webby los ha incluido como una categoría a premiar. En $2015$, el ganador fue http://www.blind.com/work/project/coldplay-ink/.
El editor de DescartesJS brinda la posibilidad de sobreponer capas transparentes, lo cual abre un gran abanico de alternativas o, si se prefiere, de diversos modelos de vídeos interactivos. En la se ilustra, en una forma simple, cómo se sobrepone al vídeo una capa transparente y un elemento de texto.
Ahora, nos concentraremos en desarrollar la actividad planteada al inicio de este capítulo, para lo cual debes descargar un vídeo y una escena interactiva, que usaremos para lograr nuestro objetivo. La descarga la puedes hacer aquí.
Descomprimes y guardas el vídeo (decimales.mp4) en una carpeta llamada videos. La escena interactiva (decimales) la dejas en el mismo sitio donde vas a crear el vídeo interactivo.

Es posible interactuar con vídeos en línea, especialmente con los subidos a YouTube, actividad que hemos dejado para un segundo nivel de este curso. Por ahora, nos preocuparemos de interactuar con el vídeo que has descargado. Observa que su formato es MP4, compatible con HTML5.
Para esta actividad usaremos elementos ya estudiados y practicados, con la excepción de dos gráficos que explicaremos en su momento. En resumen, emplearemos: siete espacios, siete controles tipo botón, un control tipo vídeo, dos algoritmos (INICIO y CALCULOS) y un evento, 21 elementos tipo gráfico (15 de ellos son textos, tres rectángulos y tres segmentos). Como puedes observar, es una actividad que se constituye, prácticamente, en una prueba final de lo estudiado, así que... manos a la obra.
E1 inicial, debe tener la siguiente configuración: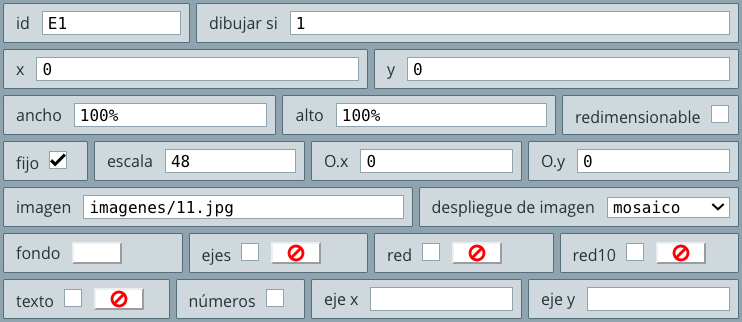
Observa que hemos usado una imagen de fondo tipo mosaico o patrón. Recuerda que puedes elegir la que desees, siempre que tengas clara la dirección relativa, te sugerimos guardar la imagen en una carpeta (imagenes) en el mismo sitio donde has creado el interactivo.
Reflexión. Comprendemos que los "paso a paso" de las actividades de cada capítulo, puedan parecer demasiado conductistas, situación que es cierta en parte, sólo en parte. Si bien hemos procurado que sigas el procedimiento indicado para cada actividad, siempre existen alternativas para lograr el mismo resultado, tales como: fondos, marcos, dimensiones, textos, posiciones, tamaños, etcétera.
El conductismo, tan vituperado, no se puede excluir en los procesos de enseñanza-aprendizaje. Como decía Rodolfo Llinás: "un niño de tanto oírle a sus padres, maestros y otros adultos que la araña pica, terminará entendiendo este evento nunca experimentado"Llinás presenta este ejemplo en el contexto de lo que denomina una conciencia colectiva, en la cual “el mandato del pueblo” es un referente para la toma de decisiones, en tanto que en éste se acumulan las experiencias, especialmente las basadas en la repetición.
What sticks in the mind is the repetition, and the sense that this knowledge evolved from the repetitive swirling of the information between and across other minds before you (Llinás, R., $2001$. I of the vortex: from neurons to self. Cambridge: The MIT Press).. No obstante la anterior defensa del conductismo, en el siguiente espacio a diseñar, comprobarás las alternativas que nuestro "paso a paso" ofrece para lograr el mismo resultado, entendido éste desde la intencionalidad del objeto interactivo en construcción. Así las cosas, en cada actividad se entremezcla el conductismo y el constructivismo pues, en últimas, estás construyendo conocimiento.
vídeo, habrás notado que aparecen los controles sin ninguna imagen de fondo. Para evitar lo anterior, se recurre a incluir una imagen previa, que se suele llamar posterEl atributo del póster especifica una imagen que se mostrará mientras se descarga el video, o hasta que el usuario presione el botón de reproducción., la cual se muestra antes de reproducir el vídeo.La inclusión de este poster se puede hacer de dos formas. La primera es guardar en la misma carpeta del vídeo, una imagen con el mismo nombre y en formato png, la cual se recomienda (por diseño) que tenga las mismas dimensiones del vídeo. La segunda alternativa es crear un espacio cuyo fondo sea una imagen del vídeo. La segunda alternativa (no necesariamente la mejor) evita que tengas que redimensionar la imagen, tal como lo explicamos a continuación.
poster con ancho 500 y alto 350 (el tamaño del vídeo), en x=100 y y=75 (posición en la escena del vídeo). Incluye, además, una imagen expandida para el vídeo:
Puedes usar esta imagen, o esta otra imagen. Al igual que la primera alternativa, la imagen sólo se mostrará "mientras se descarga el video, o hasta que el usuario presione el botón de reproducción", por lo que es necesario que en el campo de texto dibujar si, pongas la condición time=0 (esta variable la explicamos más adelante).

mascara, con las siguientes características: x=100, y=75, ancho=500, alto=350, espacio fijo, sin plano cartesiano y transparente. El objetivo de este espacio es evitar la interacción del usuario con el vídeo, es decir, oculta (máscara) propiedades de interacción del vídeo, en especial los controles. Esta restricción es necesaria para evitar que el usuario se regrese con el fin responder a las preguntas realizadas y, así, esté obligado a ver el vídeo con más atención.Obviamente, puedes tomar la decisión de no usar este espacio, si consideras que pedagógicamente no es conveniente.
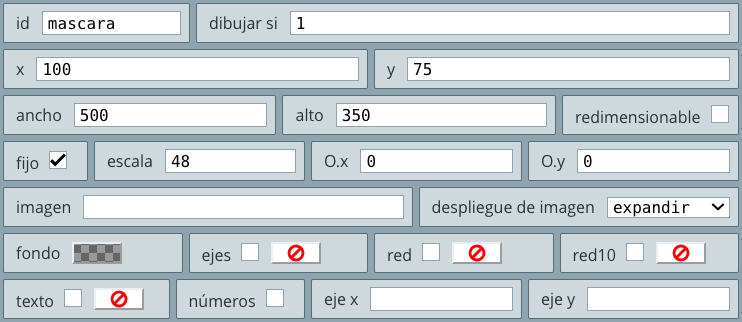
id) advertencia, en el que pondremos un mensaje advirtiendo que no se puede interactuar con el vídeo. Este espacio tiene la siguiente configuración: x=0, y=450, ancho=100%, alto=10%, espacio fijo y sin plano cartesiano. El espacio aparecerá siempre que el usuario intente interactuar con el vídeo, es decir, cuando hace clic sobre él, que equivale a hacer clic sobre el espacio máscara... por ello:
La expresión mascara.mouse_pressed significa "botón del ratón presionado en el espacio mascara".
¡No insistas! No se puede intervenir el vídeo, con color rojo, tamaño 30, coordenadas relativas, anclaje centro-centro y en la posición (0,0) (observa la siguiente figura).
Es momento de verificar como vas con tu actividad, la cual debe ser similar a la que se muestra en la siguiente página.
Prueba haciendo clic sobre la imagen (espacio mascara).
v2, expresión (100,75,500,350) y archivo videos/decimales.mp4.Antes de continuar con los botones de interacción y demás parte gráfica, vamos a configurar tres algoritmos en el selector Programa. En los dos primeros usaremos dos tipos de variables. El primer tipo corresponde a variables numéricas, con las cuales ya tienes familiaridad. El segundo tipo comprende las variables alfanuméricas, también llamadas "de cadena", pues son cadenas de caracteres; por ejemplo, en el tercer apartado usamos controles tipo texto para asignar valores a las variables N1, N2 y N3, que correspondía a los nombres de tres personas, estas variables son cadenas.
Una característica interesante de estas variables es que la expresión N1 + N2 no es una suma, es una concatenación, es decir, si N1='Juan' y N2='ito', entonces N1 + N2 = 'Juanito' (en DescartesJS el contenido de una variable de cadena, se escribe entre comillas simples).
Comprendido esto, entenderás los siguientes algoritmos:
INICIO. En este algoritmo definimos siete variables numéricas y una alfanumérica, así: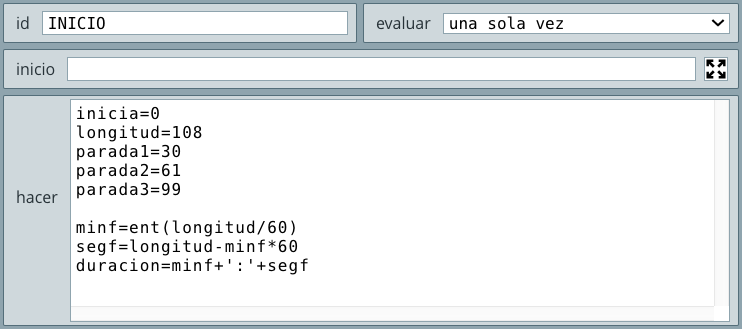
inicia=0. Es una variable que le indica al interactivo cuándo ha iniciado la reproducción del vídeo, si el valor es cero significa que aún no ha iniciado, si el valor es uno es porque hemos activado el vídeo.
longitud=108. Corresponde a la duración, en segundos, del vídeo. Para nuestro ejemplo es $108$ segundos.
parada1=30. Esta variable le indica al interactivo cuándo debe realizar la primera pausa. Los valores de la variable anterior y los de las variables de parada, en cualquier vídeo interactivo que diseñes siguiendo este modelo, los debes determinar, obviamente reproduciendo el vídeo y determinando en que momento es útil detenerlo. Hemos incluido dos pausas adicionales, puedes definir tantas pausas como estimes conveniente.
minf=ent(longitud/60). Calcula el número de minutos del vídeo. La función ent devuelve la parte entera de su argumento, es decir, la parte entera de la división longitud/60, que para nuestro vídeo es uno.
segf=longitud-minf*60. Calcula los segundos restantes: segf = 108 - 1*60 = 48.
duracion=minf+':'+segf. Es una variable de tipo cadena: duración = '1' + ':' + '48', que equivale a '1:48'. Pronto entenderás para que esta variable.
En sentido estricto las variables anteriores, por ser calculadas una sola vez, en términos informáticos son llamadas: constantes. Seguramente te extrañará que hallamos usado estas expresiones, pues al ser constantes, hubiese bastado con escribir directamente la duración, conclusión que es válida, sólo lo hicimos con fines didácticos. Escribe estas constantes y sus valores en el algoritmo INICIO, tal como se muestra en la figura anterior.
CALCULOS. En este algoritmo nos interesa calcular el tiempo de reproducción del vídeo (en cualquier momento), compararlo con las paradas definidas anteriormente para ordenarle al interactivo que detenga el vídeo y, finalmente, una variable alfanumérica similar a la anterior, pero con la duración del vídeo en un tiempo t (en cualquier momento). En este algoritmo no hay "constantes", por ello la condición evaluar siempre: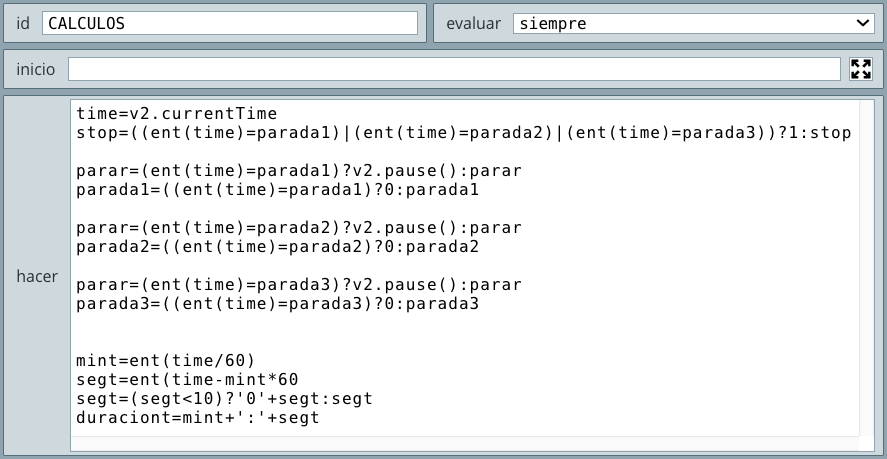
time=v2.currentTime. Calcula el tiempo de reproducción del vídeo en el instante t.
stop = ((ent(time)=parada1)|(ent(time)=parada2)|(ent(time)=parada3))?1:stop. A la variable stop se le asigna "uno" cuando la parte entera del tiempo transcurrido (time) es igual al tiempo de parada1 o (|) al de la parada2 o al de la parada3 sino, conserva su valor que inicialmente es cero.
parar=(ent(time)=parada1)?v2.pause():parar. Esta variable muda permite que se pause el vídeo, cuando el tiempo de reproducción del mismo es igual al tiempo de la primera parada.
parada1=((ent(time)=parada1)?0:parada1. Otro condicional asociado al anterior, el cual hace cero la variable parada1, pues ya ha cumplido su objetivo y hace que la marca en la línea de tiempo desaparezca.
A continuación hay dos bloques de instrucciones similares, para las paradas 2 y 3. Si vas a diseñar un nuevo vídeo interactivo, debes tener en cuenta cuántos de estos bloques necesitas. Finalmente, se calcula la duración del vídeo en un tiempo t (duraciont), en forma análoga a cómo lo hicimos en el algoritmo INICIO.
Escribe correctamente todas las instrucciones de la figura en el algoritmo CALCULOS.
Evento. El tercer algoritmo es un evento, cuyo propósito es activar la animación, la cual es necesaria para que sea eficiente la variable v2.currentTime. Agregamos este evento, así:
Hasta este momento de nuestra actividad, tenemos controlado el vídeo; sin embargo, aún no podemos afirmar que es el vídeo interactivo que pedagógicamente necesitamos pese a los botones de interacción, pues estos sólo se limitan a pausar o reproducir el vídeo. Aprovecharemos las pausas programadas en los tiempos t (time) de 30, 61 y 99 segundos, para incluir las actividades interactivas al vídeo, además de algunos textos que se presentarán en los momentos adecuados.
t) en el que se esté reproduciendo el vídeo, lo que hará el interactivo mas dinámico y atractivo. Hemos destinado la parte superior de la escena, para la presentación de estos textos. El primero de ellos es el título inicial, para el cual sugerimos la siguiente configuración:
Observa que este título sólo aparecerá antes de la reproducción del vídeo. El título central del vídeo lo dejaremos para el final, pues depende de la aparición de otros textos. Recuerda que para el diseño de los textos con coordenadas relativas, es recomendable dejar, en principio, el plano cartesiano.
(0,4), tamaño 28 y anclaje centro-centro, los cuales deben aparecer durante la reproducción del vídeo o en las pausas programadas, así:Observa bien el vídeo\nTe haremos algunas preguntas, con condición: (time>2)&(time<5)Primera pregunta\n¿Es correcta la afirmación?, con condición: (stop=1)&(parada1=0)&(parada2>0)Segunda pregunta\n¿Es correcta la afirmación?, con condición: (stop=1)&(parada2=0)&(parada3>0)¡Sigue atento!\nObserva el siguiente ejercicio, con condición: (time>44)&(time<48)El vídeo se produjo sobre una escena interactiva\ndiseñada por José Luis Abreu León, con condición: (time>67)&(time<98)Ahora es tu turno. Resuelve el ejercicio, arrastrando \nlos números a las casillas correspondientes, con condición: (time>99)&(time<102)Sólo te explicamos el texto correspondiente a la parada2, los demás quedan para tu análisis: el texto se presenta cuando la variable time (tiempo de reproducción del vídeo) alcanza el valor de la variable parada2. En este momento, la variable stop es igual a uno, puesto que el primer condicional del algoritmo CALCULOS se hace verdadero, ya que ent(time)=parada2. Pero, no sólo basta con cumplir este condicional, también se requiere que se cumpla que la variable parada2 sea igual a cero, igualdad que se obtiene en el algoritmo anterior, a través del siguiente condicional: parada2=((ent(time)=parada2)?0:parada2. Finalmente, es necesario que también se cumpla que parada3 sea mayor que cero, situación que es cierta en el momento en que el tiempo t (time) es igual al de parada2.
Inicialmente, vamos a dibujar un rectángulo en la parte inferior del vídeo (espacio mascara), con fondo negro. Este rectángulo será el fondo sobre el que dibujaremos la línea de tiempo.
Pero, antes de continuar, lee el siguiente texto que te ilustra sobre este nuevo componente gráfico:
Retornando a nuestro primer rectángulo, éste lo diseñamos usando la siguiente expresión: (-5.16,-3,10.33,-.7), con color y relleno negro. Recuerda que las dos primeras coordenadas indican el primer vértice del rectángulo y su identificación se logra con el plano cartesiano activado.
El segundo rectángulo nos dibujará la línea de tiempo. La expresión a usar es (-3.3,-3.42,8,.2), de color blanco, sin relleno y radio de borde 6.
El último rectángulo es igual al anterior, pero cambiando la tercera coordenada por una expresión variable: (-3.3,-3.42,8*time/108,.2), que indica un rectángulo de largo variable, dependiendo de la reproducción del vídeo. Debes ponerle relleno, que puede ser blanco, además del radio de borde 5.
(-3.3+8*parada1/108,-3.5)(-3.3+8*parada1/108,-3.15)(-3.3+8*parada2/108,-3.5)(-3.3+8*parada2/108,-3.15)(-3.3+8*parada2/108,-3.5)(-3.3+8*parada2/108,-3.15)Los tres segmentos tendrán un tamaño 2 y un ancho 4. Los dos primeros corresponden a actividades de evaluación, por lo que los distinguiremos con un color naranja. El tercer segmento es una escena interactiva, al cual le hemos asignado un color verde. Lo de los colores queda a tu gusto.
texto (selector Gráficos), con contenido [duraciont]/[duracion], expresión (-4.9,-3.2), color blanco y tamaño de fuente 14.Agregados estos elementos gráficos (en el espacio mascara), el diseño de la línea de tiempo quedaría así:

Seguramente, estarás protestando por la cantidad de trabajo realizado para este actividad. Si te sirve de aliciente, estás obteniendo una plantilla para diseñar muchos vídeos interactivos, en los cuales sólo tendrías que cambiar tiempos de parada, número y tipo de actividades interactivas.
Para ello, debes agregar un espacio por cada actividad:
Espacio primera actividad evaluativa. Agrega un espacio con identificador (id) preg1, en x=130, y=270, ancho 440, alto 110, fondo semitransparente (18 está bien) y condición para dibujarse: (stop=1)&(parada1=0).
Espacio segunda actividad evaluativa. Tiene la misma configuración del anterior, cambiando el identificador por preg2 y la condición por (stop=1)&(parada2=0).
Espacio para escena interactiva. Agrega un espacio HTMLIframe con x=90, y=35, ancho 515, alto 400, condición dibujar si (stop=1)&(parada3=0) y archivo decimales/index.html, que corresponde a la escena interactiva que previamente descargaste.
Ahora, sólo nos resta incluir los elementos de las dos primeras actividades, puesto que la tercera ya está previamente diseñada.
casilla de verificación. Agrega, entonces, dos controles de este tipo, así: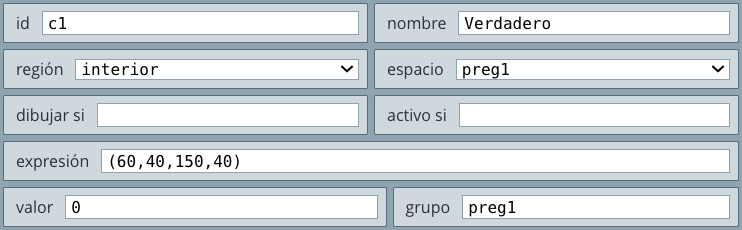
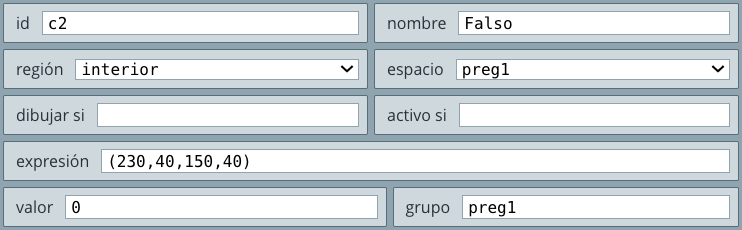
Observa que estos controles están asociados al espacio preg1.
c3 y c4, asociados al espacio preg2.Para cada una de estas actividades, vamos a agregar los siguientes textos:
Espacio preg1.
Texto: ¡Está bien escrito el número!, expresión: (0,.8) en coordenadas relativas, con color: verde y tamaño: 28.
Texto: ¡Correcto!, expresión: (0,-.8) en coordenadas relativas, con color: verde, tamaño: 28 y condición c2=1 (observa que la afirmación es falsa).
Texto: ¡Incorrecto!, expresión: (0,-.8) en coordenadas relativas, con color: rojo, tamaño: 28 y condición c1=1.
Espacio preg2.
Los mismos tres textos, pero... piensa un poco y agrega los textos que corresponden.
botón que sólo aparezcan cuando el usuario responda correctamente la pregunta. Obviamente, para este tipo de evaluación no hay problema para el usuario, pues si responde incorrectamente, tiene la opción de marcar la otra respuesta. No obstante, es posible diseñar otro tipo de preguntas cuya respuesta exija mayor comprensión de lo visto en el vídeo (respuesta tipo texto, por ejemplo).Agrega, entonces, los siguientes controles tipo botón en el espacio E1 en su interior.
Id botón: preg1, nombre: Continuar vídeo, condición: (stop=1)&(c2=1)&(parada2>0), expresión: (256,455,188,42), acción: calcular, tamaño fuente: 24 y parámetro: stop=0;v2.play().
Analiza la condición y los parámetros y trata de comprender su significado lógico.
Id botón: preg2, igual configuración al anterior, sólo cambia la condición por: (stop=1)&(c3=1)&(parada3>0).
Id botón: preg3, igual configuración al anterior, sólo cambia la condición por: (stop=1)&(parada3=0).
Texto: Vídeo Interactivo\nLectura de decimales, expresión: (0,4) en coordenadas relativas, tamaño: 30, anclaje: centro-centro y dibujar si: (time>6)&(stop=0)&((time<44)|(time>48))&(time<66).
Analiza el porqué está última condición.
v2.currentTime sólo es eficiente si hay una animación en curso. En el diseño de nuestro vídeo hemos incluido la instrucción inicia=1 en el botón Reproducir y, además, el evento que activa la animación cuando esta instrucción se ejecuta. En el selector Animación realiza la siguiente configuración:
Puedes observar que la animación será permanente, pues el mientras ccosa=0 siempre será verdadero.
¡Eso es todo!
Diseña un vídeo interactivo. Elige el vídeo y al menos dos actividades interactivas.
Si te sirve de ejemplo, el siguiente vídeo interactivo utiliza otro formato de pregunta.
Otra alternativa es usar las plantillas de DescartesJS que puedes consultar en http://proyectodescartes.org/plantillas/objetos.htm. Son plantillas sencillas de editar, tal como se indica en este vídeo: https://youtu.be/HrPYdPsdqT4.
En el siguiente vídeo resumimos la introducción a este capítulo.
En el libro DescartesJS - Nivel 2, diseñaremos otros tipos de vídeos interactivos que permiten la comunicación con aplicaciones como GeoGebra o con los parámetros disponibles en la API de YouTube.
Al terminar este capítulo, habrás desarrollado la siguiente actividad:
En esta actividad utilizaremos controles gráficos, funciones, vectores, animación, textos en coordenadas relativas, diseño JavaScript de botones, cambio de estilos de fuente y, en especial, las familias de gráficos.
Inicialmente, debes descargar una carpeta de trabajo que puedes descargar aquí. El contenido de esta carpeta es el siguiente:
index.html, es el archivo que ejecuta la actividad y el que vamos a modificar con el editor DescartesJS.imagenes, que contiene 12 imágenes a usar en el diseño de la actividad.images, que contiene la imagen de fondo.lib, que contiene el intérprete DescartesJS.fonts, que contiene una fuente especial que usaremos al final de la actividad.El archivo index.html sólo presenta la configuración del espacio de trabajo, el objetivo es construir la actividad siguiendo las instrucciones que se dan a lo largo de este capítulo. El diseñador es libre de cambiar algunos elementos de diseño, como imágenes, los textos, máxima calificación y número de ejercicios. Comprendida la actividad, se pueden emprender otras actividades similares o esta misma con un mayor número de contenedores.
Una vez abras el archivo index.html (Archivo → Abrir), observarás que la escena tiene dimensiones $790\times 500$ y, además, la opción escalar en el parámetro expandir escena, la cual asegura que si el espacio en el navegador es más grande que el de la escena original, se reescale todo el espacio hasta ajustarse al tamaño en el navegador.
Las imágenes que vamos a usar (carpeta imagenes) las hemos obtenido de la página http://www.dedominiopublico.org/, la cual ofrece revistas y películas que, por su antigüedad, son de dominio público. El criterio de selección, el nombre y el tamaño de las imágenes, las explicamos más adelante.

Los dos primeros tríos de imágenes son capturados de la revista de cómics TBO y, los dos últimos tríos, de dos películas de Disney de $1937$ (limpiadores de relojes y fantasmas solitarios).
El fondo de el espacio de trabajo, será una imagen que se encuentra en esta ruta relativa: images/fondo.jpg (Ver ). Por su tamaño reducido ($120\times 120$ pixeles) y por ser del tipo patrón, seleccionamos como despliegue de la imagen la opción mosaico. Obviamente, puedes elegir otra imagen de fondo o sólo usar un color de fondo.
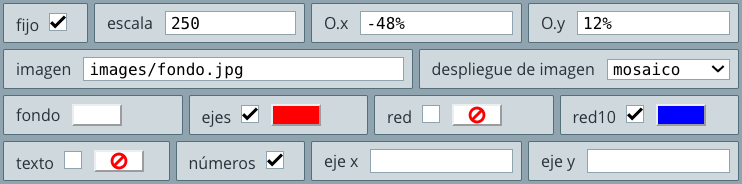
Como vimos anteriormente, una de las estructuras más utilizadas en programación es el ciclo o bucle tipo Do-While (hacer–mientras), cuyo propósito es ejecutar un bloque de código y repetir la ejecución mientras se cumpla cierta condición expresada en la cláusula while, tal como se observa en la :
En código JavaScript, un ejemplo de este tipo de ciclo sería:
i = 1;
do {
document.write(i);
i = i + 1;
} while (i<10);
Cuyo propósito es escribir los números naturales del 1 al 10.
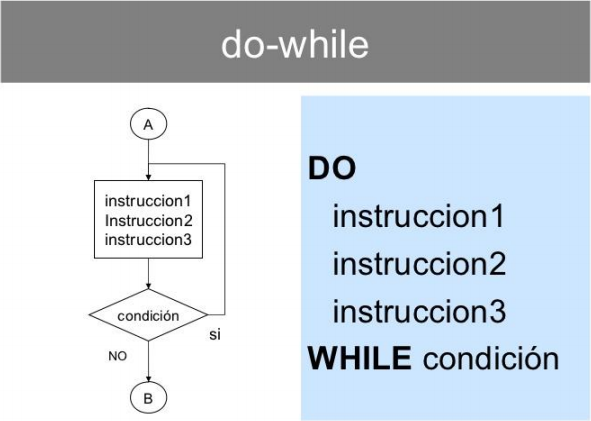
Una variante del código anterior, que nos permitirá acercarnos al funcionamiento de las familias de DescartesJS, sería el siguiente:
i = Inicia;
do {
function Dibujar_Poligono(i);
i = i + Incremento;
} while (i<Termina);
En el que se presenta una llamada a una función que dibujará un polígono, es decir, se dibujarán tantos polígonos como la condición del while sea verdadera.
Ya hemos visto que en el editor DescartesJS hay varias formas de crear algoritmos con la estructura Do-While. En la observamos dos ejemplos, el primero corresponde a una función (selector Definiciones), que muestra los números naturales del 1 al 9 (verifica por qué hasta nueve). El segundo algoritmo corresponde a una animación, que explicaremos al final de esta actividad.
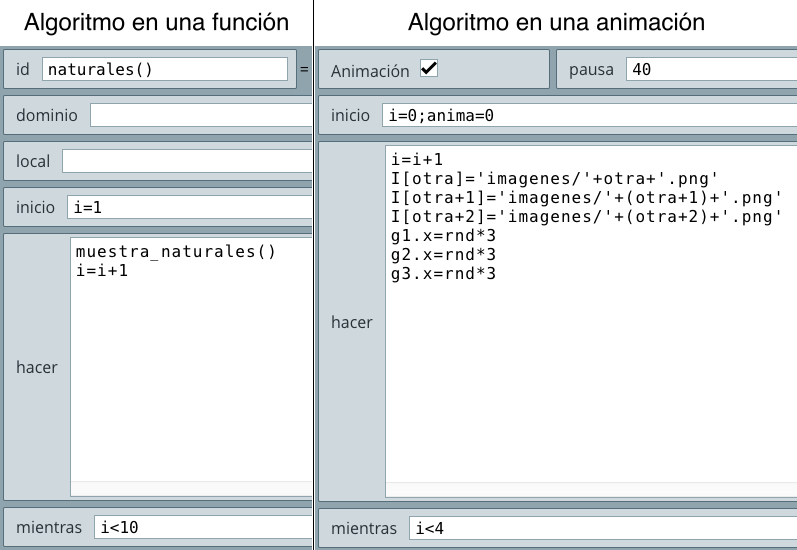
Otra de las opciones interesantes de DescartesJS es el uso de familias para el diseño de gráficos. El funcionamiento de esta opción es similar al de un ciclo o bucle tipo Do-While. En DescartesJS, el segundo ejemplo Do-While en código JavaScript sería de la siguiente forma:

En el selector Gráficos hemos creado un polígono cuyas coordenadas varían con la variable i (observa que está activada la opción familia). Esta variable toma valores según el intervalo, es decir, desde un valor inicial que hemos llamado Inicia, hasta un valor final Termina, el incremento depende del número de Pasos definidos, que se calcularía así: Incremento = (Termina – Inicia)/Pasos. Veamos unos ejemplos para un intervalo [0,6] y diferentes valores de la variable pasos:
En DescartesJS podemos crear familias de cualquier tipo de gráfico. Algunos ejemplos se muestran en la siguiente escena interactiva:
Ahora, vamos a nuestra actividad. Nuestra tarea es dibujar tres polígonos que se constituirán en los contenedores en los cuales irán en orden secuencial las imágenes. Alguien podría decir que bastaría con dibujar tres rectángulos y olvidar lo de las familias, conclusión que es cierta, pero el uso de familias facilita el diseño de plantillas similares con 4 o más contenedores, tal como están publicadas en el proyecto Plantillas de DescartesJS, además de otros diseños en los cuales las familias son fundamentales (los puzles, por ejemplo).
Nuestro espacio de diseño, como vimos antes, es de $790\times 500$ pixeles que, desde un análisis aritmético simple, nos permite inferir que un ancho de $250$ para nuestros contenedores sería el adecuado. Este ancho determina la escala que usaremos en nuestro espacio de trabajo, tal como se aprecia en la siguiente figura:

La posición del origen de coordenadas la hemos desplazado, de tal forma que podamos dibujar nuestros polígonos en el primer cuadrante así: desplazamiento del eje $y$ en un 48% a la izquierda, esto significa que el eje $y$ queda casi en el borde izquierdo del espacio de trabajo (inicialmente estaba en el centro del espacio, por ello lo de 48%);
desplazamiento del eje $x$ en un 12% hacia arriba, este valor se puede ajustar de tal forma que quede el espacio suficiente para los títulos y las imágenes, es decir, a medida que avances en el diseño de la actividad puedes regresar a este paso para cambiar la posición del origen de coordenadas.
Nuestras imágenes provienen de tiras cómicas que, generalmente, tienen un valor mayor en el ancho. Partiendo de esta premisa, hemos escogido como tamaño de imágenes de $250\times 200$ pixeles. Así las cosas, la familia de polígonos a construir es la siguiente:

Con un fondo de color amarillo y transparencia ae, el resultado es el que se observa en la figura de la página siguiente.
Recuerda que el fondo del espacio es la imagen fondo.jpg con despliegue mosaico, hemos dejado, por ahora, los ejes en color azul. Observa que los tres polígonos inician en i=0, i=1 y i=2.
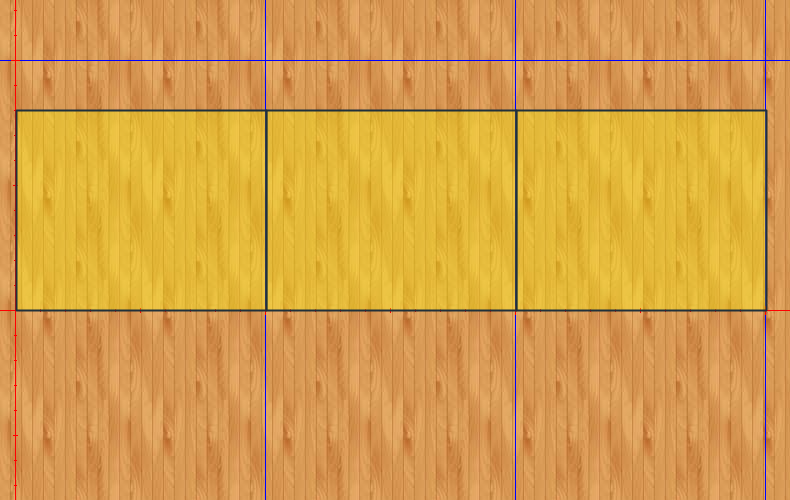
Como nuestro propósito es arrastrar imágenes a los contenedores, necesitamos tres controles gráficos a los cuales asociaremos las imágenes. Estos controles tendrían la siguiente configuración:
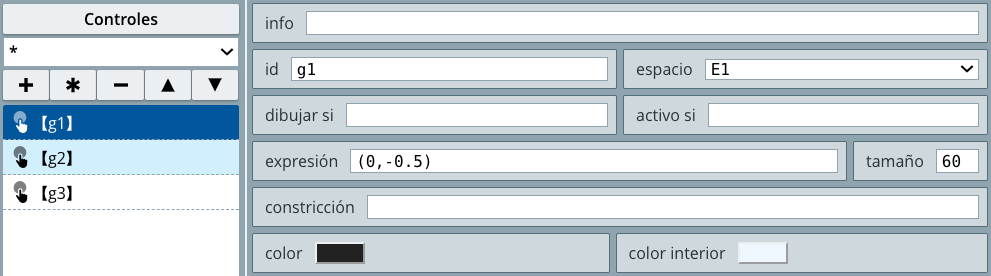
Inicialmente ubicados en (0,-0.5), (1,-0.5) y (2,-0.5) para g1, g2 y g3 respectivamente, de un tamaño de 60, tal como se aprecia en la siguiente figura:
En el selector Definiciones creamos un vector I que contendrá las imágenes que vamos a usar. En principio, hemos dejado un tamaño de cien (100), suficiente para una treintena de ejercicios y, obviamente, para los cuatro de nuestra actividad. Es importante definir los elementos del vector, así: I[1]='imagenes/1.png', I[2]='imagenes/2.png' y así sucesivamente hasta la última imagen a usar en la actividad.
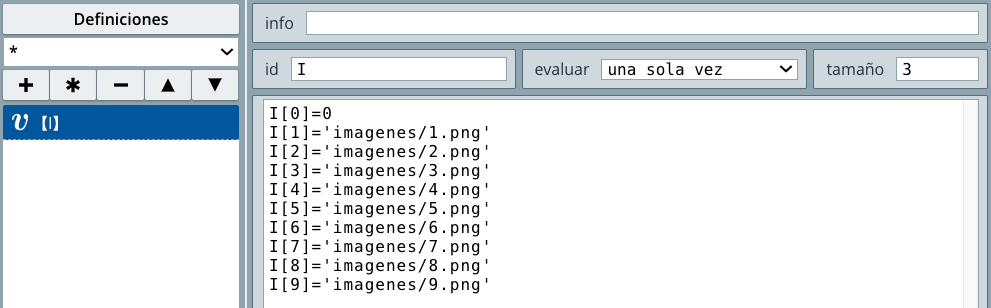
Nuestras imágenes se irán mostrando dependiendo del ejercicio que se esté ejecutando, por ello, hemos definido dos variables en el algoritmo INICIO, iniciadas en uno (1).
La variable otro determina el ejercicio en ejecución, inicialmente uno para el primero. La variable otra determinará el número de la primera imagen correspondiente a ese ejercicio, uno para el primer ejercicio. Las variaciones correspondientes a estas variables las veremos más adelante.
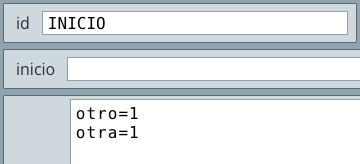
Nuestro siguiente paso es agregar las imágenes en el opción gráficos. Para ello, agregamos una primera imagen cuya configuración es la siguiente:
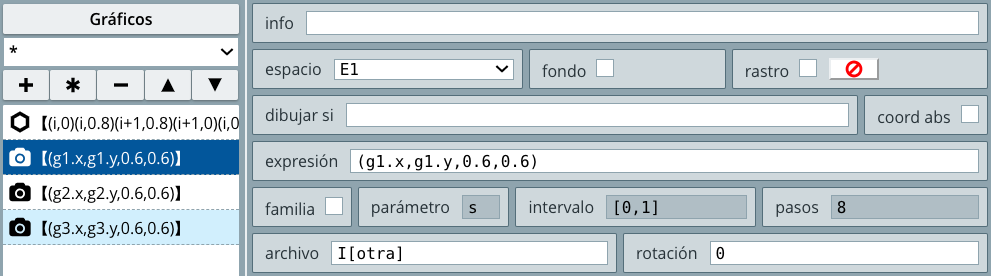
La expresión (g1.x,g1.y,0.6,0.6) significa lo siguiente: los dos primeros términos indican la posición de la imagen, es decir, se encontrará donde esté el control gráfico g1, igual para las otras dos imágenes asociadas a los controles g2 y g3; los dos últimos valores indican el escalamiento de la imagen, es decir, un ancho y un alto del 60% del tamaño original. Ahora, el archivo que contiene la primera imagen se carga a través el elemento I[otra], donde la variable otra tiene un valor de uno (1), el archivo para la segunda imagen es I[otra+1], y para la tercera I[otra+2]. Así las cosas, obtendríamos lo siguiente:
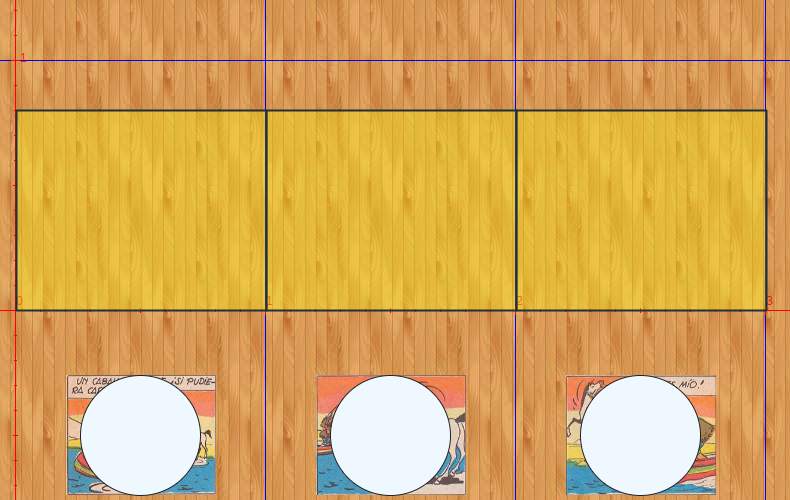
Es importante que comprendas que todo control gráfico tiene unas coordenadas asociadas. Si el control está identificado (id) como gn, sus coordenadas asociadas son (gn.x,gn.y).
El tamaño de 60 para el control gráfico, ahora es comprensible. Obviamente, no nos interesa que el control se muestre en nuestro espacio de trabajo, por ello, dejaremos un valor cero (0) en la casilla dibujar si, que tendrá como efecto la desaparición visual de los controles.
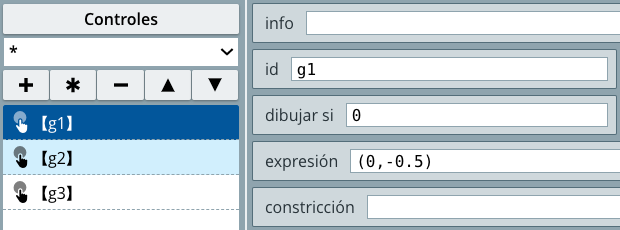
Resumiendo, nuestra actividad tendría la siguiente presentación (interactúa con ella):
Una última acción sobre las imágenes, que haremos en este apartado, es el cambio del tamaño cuando las imágenes están cerca de los cajones o contenedores. En la imagen anterior se observa que los tamaños de las imágenes están reducidas, lo cual se hizo intencionalmente para que cupieran en el espacio inferior de la escena. Intervendremos los dos últimos valores de la expresión de cada imagen, sumándoles 0.4*(g1.y>0), es decir, cuando arrastremos la imagen hacia arriba, una vez que sobrepasemos el eje $x$, el tamaño se aumentará en 0.4, obteniendo su tamaño original. Para las otras imágenes es similar, cambiando el control gráfico.

El efecto sobre la actividad se puede observar en la siguiente imagen:

Un efecto adicional es generar rotaciones en las imágenes que desparecerán una vez las arrastremos hacia los contenedores. Para ello, hemos incluido una función que denominamos rota(). Esta función la invocamos una sola vez por ejercicio, para el primer ejercicio escribimos en el algoritmo de inicio:
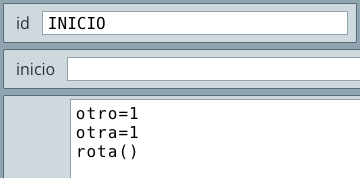
En el selector Definiciones creamos la función rota(), así:
Esta función será un algoritmo con las siguientes instrucciones:
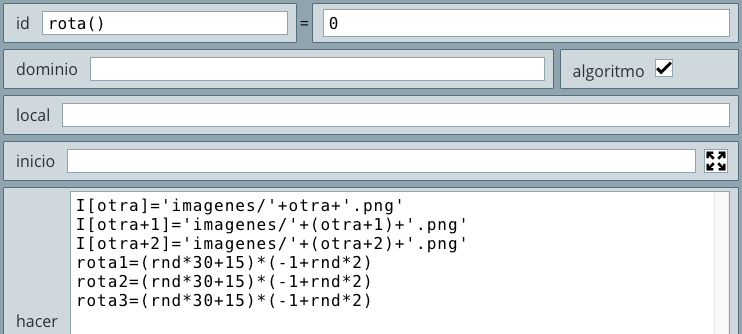
Las tres primeras instrucciones asignan a los elementos I[otra], I[otra+1] y I[otra+2], las imágenes correspondientes a cada ejercicio que, para la primera secuencia de imágenes sería I[1]='imagenes/1.png', I[2]='imagenes/2.png' y I[3]='imagenes/3.png'. A continuación, se generan tres valores asociados a las variables rota1, rota2 y rota3, valores aleatorios entre 0 y 45 (obtenidos por rnd*30+15), cada uno de estos valores se multiplican por la expresión, también aleatoria, (-1+rnd*2), la cual asigna un valor positivo o negativo a las rotaciones.
En nuestras imágenes incluiremos en la casilla rotación la expresión rota1*(g1.y<0). Para la otras dos: rota2*(g2.y<0) y rota3*(g3.y<0), que significa asignar las rotaciones antes creadas, mientras las imágenes estén por debajo del eje $x$.

Así, entonces, nuestra actividad tendrá esta apariencia:
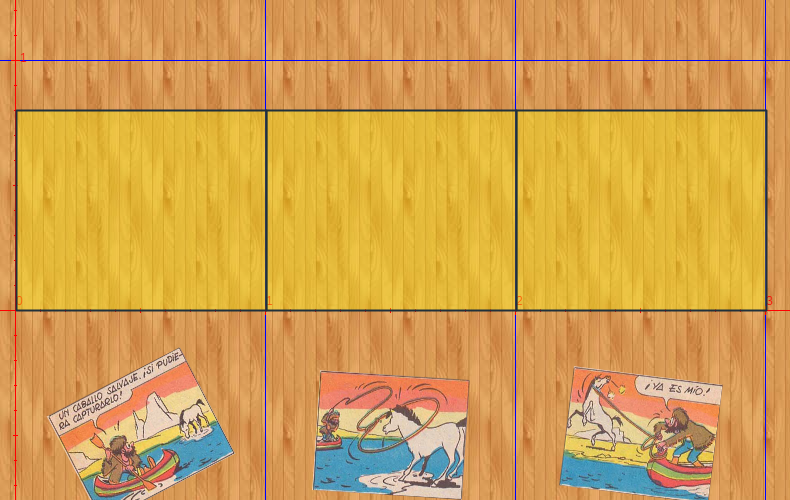
Seguramente, te estarás preguntando sobre el funcionamiento y la notación de la función rota(). En el siguiente texto, puedes aclarar dudas al respecto. Observa el ejercicio que ilustra las ventajas de una programación modular, a través del uso de la definición: función.
Nuestros siguientes pasos están centrados en evitar que las imágenes se salgan del espacio de trabajo y se ajusten adecuadamente a los contenedores. Por otra parte, debemos verificar que la ubicación de cada imagen esté en la posición correcta.
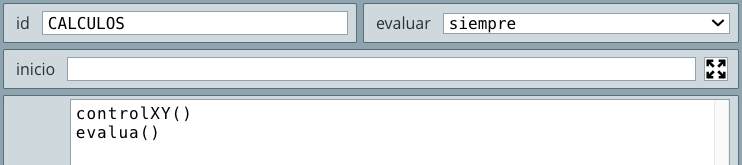
En el algoritmo CALCULOS incluiremos el llamado a dos funciones. La primera la hemos denominado controlXY(), la segunda la llamamos evalua(). Teniendo como referencia la escena que hemos diseñado hasta este momento, explicaremos la primera función.
Función controlXY(). Debemos evitar que el control gráfico g1 asociado a la primera imagen se desborde del espacio de trabajo. Las instrucciones que permiten evitar este desborde son:
g1.y=(g1.y>0.4)?0.4:g1.y g1.y=(g1.y<-0.5)?-0.5:g1.y g1.x=(g1.x<0.5)?0.5:g1.x g1.x=(g1.x>2.8)?2.8:g1.x
Si observamos la escena, el tope superior está en la mitad de los cajones, es decir, en 0.4, para evitar un desplazamiento más arriba de este valor usamos la estructura condicional g1.y = (g1.y>0.4)?0.4:g1.y, la cual podríamos explicar desde su forma en diagrama de flujo:
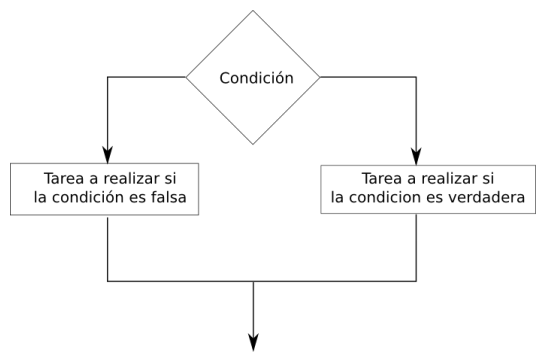
La condición es (g1.y>0.4), si es verdadera se ejecuta la instrucción que está después del signo ?, es decir, g1.y=0.4 (la ordenada del control gráfico será igual a 0.4, siempre que ésta supere ese valor); si es falsa, se ejecuta la instrucción que está después del signo :, es decir, g1.y = g1.y (no cambia la ordenada del control gráfico). Igual análisis puedes hacer para las otras instrucciones, las cuales evitan que la ordenada del control gráfico sea menor a -0.5 y, además, que su abscisa no sea inferior a 0.5 ni superior a 2.8.
Por otra parte, debemos garantizar que la imagen quede incrustada en alguno de los tres contenedores, para lo cual recurrimos al siguiente condicional: g1.x=(g1.y>0)?ent(g1.x)+0.5:g1.x. El cual fija la abscisa al centro de los cajones (0.5, 1.5 o 2.5). Estas mismas instrucciones las replicamos a los otros controles gráficos.
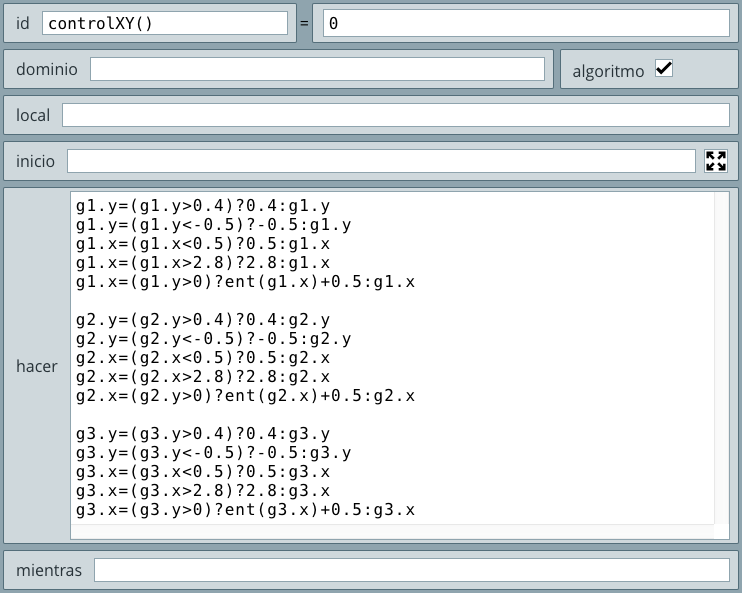
Función evalua(). Para esta función hemos creado, inicialmente, un vector C, que permitirá almacenar las posiciones correctas (1) o no (0) de las tres imágenes.
La secuencia estará bien colocada si la primera imagen está en la posición g1.x = 0.5 y g1.y = 0.4, la segunda imagen en g2.x = 1.5 y g2.y = 0.4 y la tercera en g3.x =2.5 y g3.y = 0.4. Si lo anterior ocurre, C[1], C[2] y C[3] serán iguales a uno (1).
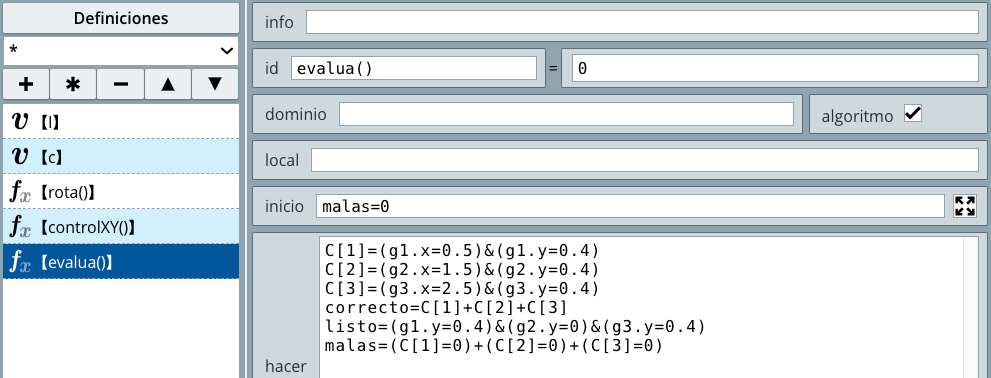
El algoritmo de la función incluye, además, las siguientes variables:
correcto. Es la suma de los tres elementos del vector C, para una secuencia correcta su valor debe ser tres (3).listo. Es igual a uno (1) cuando todas las piezas están en los contenedores.malas. Es la suma de las piezas mal colocadas, es decir, la suma de los elementos del vector C que valen cero (0).Verifica que la actividad la has realizado correctamente hasta este apartado; para ello, observa el siguiente vídeo, el cual te indica cómo debe estar funcionando el objeto interactivo. Puedes desactivar el plano cartesiano.
Siempre que estemos diseñando una actividad con DescartesJS debemos adoptar el papel de usuario, pues ello nos permitirá incluir algunas acciones que hacen la actividad mas atractiva o divertida para los demás usuarios. Por ejemplo, una vez se ubiquen las piezas en los cajones, podríamos optar por presentar los mensajes de acierto o error, lo que nos obligaría a inactivar los controles gráficos, impidiendo alguna corrección. Para evitar esta situación, es preferible usar un botón de verificación, en el que el usuario hará clic una vez esté seguro de su respuesta.
Diseñamos, entonces, este botón así:
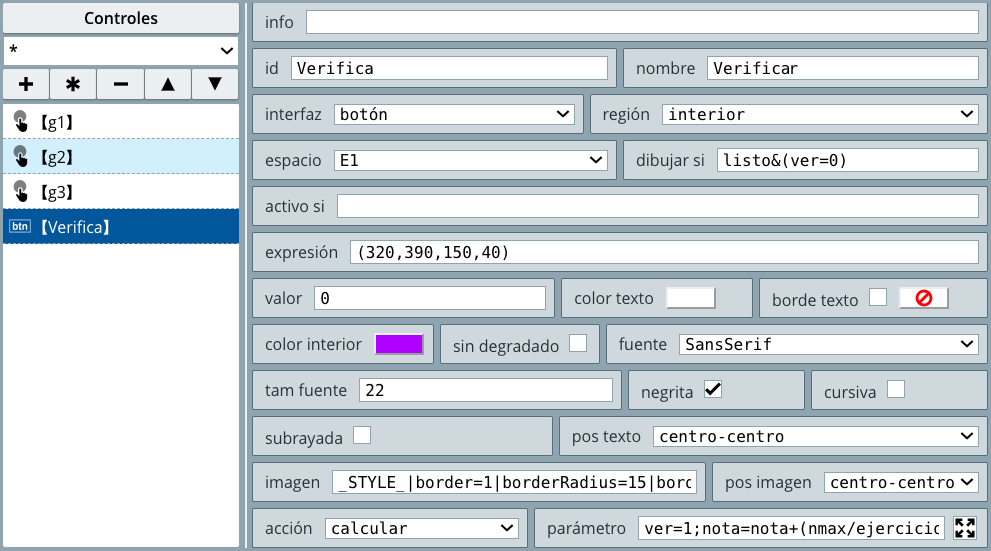
El texto del botón será Verificar en negrita y tamaño 22 con los colores mostrados en la figura anterior, lo hemos centrado horizontalmente en 320 (este valor se obtiene restando el ancho de 790 y dividendo por dos), su ancho es 150 y el alto de 40.
La acción es calcular con las siguientes instrucciones:
ver=1 nota=nota+(nmax/ejercicios)-(malas/3)*(nmax/ejercicios)
La variable ver, cuando vale uno (1), nos servirá para mostrar el segundo botón y los textos.
La variable nota almacena la calificación de la actividad. Las demás variables de la expresión las hemos definido en el algoritmo INICIO:
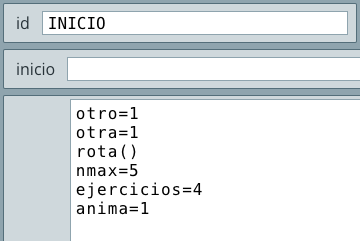
Aquí es importante observar que a medida que avanzamos en el diseño de una actividad, tendremos que intervenir pasos anteriores, como es el caso de este algoritmo; en otras palabras, la programación de una actividad no es posible hacerla en forma lineal, siempre tendremos que retornar a los pasos anteriores.
Continuando con las instrucciones, la variable nmax tiene un valor de cinco (5), que corresponde a la nota más alta de calificación, valor que puede ser cambiado según la escala de calificación utilizada en el entorno del diseñador (20 en Venezuela, por ejemplo). La variable ejercicios tiene un valor de cuatro, que es la cantidad de ejercicios de esta actividad, igualmente la puedes cambiar.
Ahora, con estos valores entenderemos la expresión que calcula la nota. Por cada ejercicio, sumará a la nota (nmax/ejercicios o 5/4 o 1.25), que para los cuatro ejercicios sería un total de cinco (5). Por cada pieza mal colocada, la nota se castigará en (malas/3)*(nmax/ejercicios), es decir, si tenemos dos piezas mal ubicadas, la nota se reduce en (2/3)*1.25.
El botón se muestra cuando la variable listo es igual a uno (ver función evalua()) y ver es cero.
Finalmente, hemos incluido un diseño especial al botón en la casilla imagen. Si está casilla la dejamos en blanco, el diseño del botón es el que trae por defecto DescartesJS, también es posible usar una imagen o, para nuestro caso, la siguiente expresión de DescartesJS:
_STYLE_|border=1|borderRadius=15|borderColor=ffffff|
overColor=e0a12b|downColor=ff0000|font=Monospace|
shadowTextColor=000000|shadowBoxColor=808080
Puedes probar diferentes valores para los colores, el radio de los bordes del botón y tipo de fuente. En la siguiente imagen, se observa cómo va nuestra actividad:
Como lo advertimos antes, una vez el usuario haga clic en este botón, los controles gráficos deben inactivarse, para ello, incluimos la expresión ver = 0 en las casilla activo si. Observa que cuando hacemos clic en el botón Verificar a la variable ver se le asigna el valor de uno (1), que tiene como primer efecto la inactivación de los controles gráficos.

Botón Otro ejercicio. Su diseño es similar al anterior botón, por lo que nos detendremos sólo en las instrucciones de cálculo y en la casilla dibujar si. En los parámetros iniciales el único cambio es el tamaño de fuente, que para este botón es de 20.
El botón debe aparecer una vez se haga clic en el botón Verificar y, obviamente, existan aún ejercicios por resolver, por ello, en la casilla dibujar si debemos escribir la siguiente condición:
(ver=1)&(otro<ejercicios).
Cuando se hace clic en este botón, las instrucciones que se ejecutan son las siguientes:
otro=otro+1. Aumenta en uno la variable otro, que responde al número de ejercicio en curso.otra=3*(otro-1)+1. Habíamos explicado que esta variable está asociada al número de la imagen a mostrar. Por ejemplo, si el ejercicio que se está desarrollando es el cuarto (otro = 4), la variable otra tomará el valor de 3*(4 – 1) + 1 = 10, la imagen asociada sería: 10.png.ver=0. Al retornar a cero esta variable, se oculta el botón, pues no cumpliría la condición (ver=1)&(otro<ejercicios).g1.y=-0.5. Retorna la primera imagen a la parte inferior de la escena.g2.y=-0.5. Retorna la segunda imagen a la parte inferior de la escena.g3.y=-0.5. Retorna la tercera imagen a la parte inferior de la escena.anima=1. La variable anima la usamos para ejecutar una animación, que explicaremos al final de este instructivo.Dibujaremos dos polígonos adicionales, que deben estar después de las imágenes. Un polígono igual al primero que diseñamos, pero sin relleno. Su utilidad es evitar que se pierdan los bordes de los cajones una vez estén colocadas las imágenes, como se muestra en la siguiente imagen.

El polígono se debe dibujar cuando las imágenes estén colocadas; es decir, cuando la variable listo es igual a uno (1).
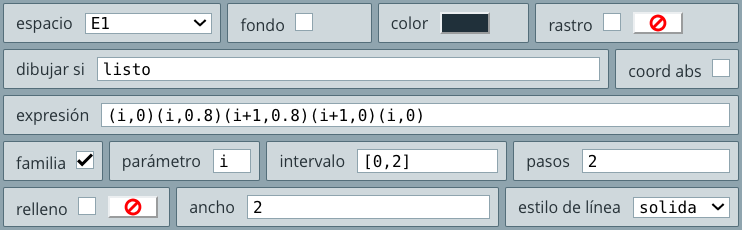
Nota que en la casilla dibujar si hemos puesto la variable listo sola, esta expresión, para DescartesJS, es equivalente a listo = 1. Observemos su efecto:

El otro polígono tiene como función dibujar cajones con relleno colorado para las imágenes mal puestas. Para ello, copiamos el polígono original, en el cual hacemos los siguientes cambios: el color de relleno es rojo con transparencia.
La condición para mostrar los cajones es (C[i+1]=0)&(ver=1); es decir, se muestra el contenedor colorado cuando se hace clic en el botón verificar y el elemento del vector C es cero (pieza mal puesta).
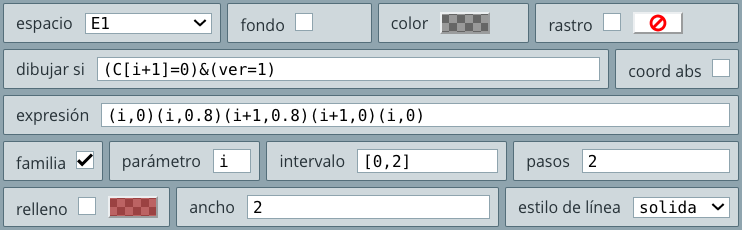
Un ejemplo del efecto de este polígono se muestra en la siguiente figura:

Ya estamos llegando al final de nuestra actividad. Los textos que usaremos tendrán algunas características especiales que debes considerar para los efectos finales de la actividad. En primer lugar, usaremos textos en formato simple, el cual basta con escribirlo en la casilla de texto o, si se prefieres, hacer clic en el botón de Texto simple (marcado con la letra mayúscula T).
Título de la actividad. Tal como aparece en la siguiente figura. Las coordenadas relativas en (1.5,1.15), tamaño de fuente en 30 y borde para el texto.
Instructivo. Es el texto que instruye sobre lo que hay que hacer en la actividad.
Cambio de fuente. Seguramente ya habrás notado que el texto correspondiente al botón de otro ejercicio, no se ajusta al ancho del botón, algo que se soluciona cambiando el ancho o el tipo de fuente. Una de las carpetas que acompañan esta actividad es una que hemos llamado fonts, la cual contiene varios tipos de fuente que usaremos para nuestros textos, para ello, debes incluir en el archivo index.html (usa un editor de texto sin formato), un vínculo, tal como aparece en la siguiente figura:

Verifica si el archivo index.html tiene esa línea, sino la puedes escribir luego de la etiqueta <title>.
Nuestra actividad, para este tipo de fuente, tendrá la siguiente presentación:
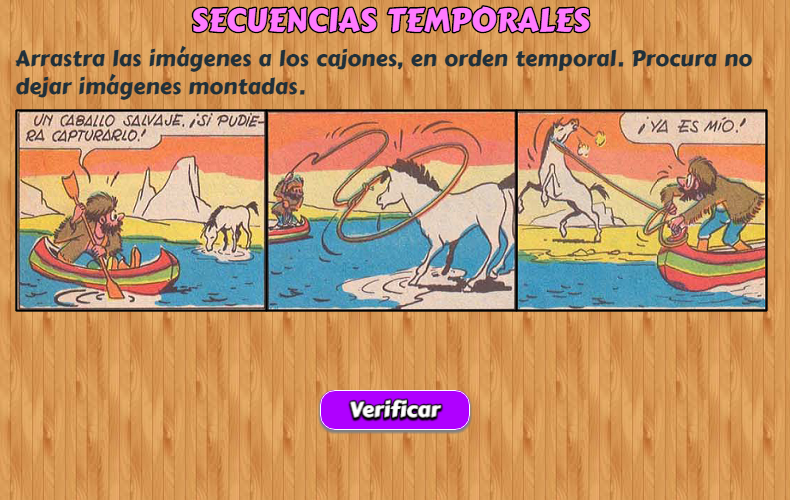
En la carpeta fonts encontrarás $16$ tipos de fuente, puedes practicar cambiando la fuente en el vínculo anterior. Algunos ejemplos, son:

Si deseas generar otros tipos de fuente, te presentamos un procedimiento sencillo para obtenerlas:
Encontrando fuentes. En primer lugar, accede a una página que te permita descargar las fuentes en tipografía tipo True Type Font (ttf) u Open Type Font (otf), una de ellas es https://www.fontsquirrel.com/fonts/
Una vez descargada la fuente, debemos generar un código base64, el cual se puede lograr desde la página anterior desde la opción Generator: https://www.fontsquirrel.com/tools/webfont-generator. Los pasos son simples, subes la fuente (Upload fonts), seleccionas EXPERT, formato WOFF.
Es importante activar la opción Base64.
Una vez descargada la fuente (Download your kit), abrimos el archivo stylesheet.css y copiamos todo el código que hay después de src. Este código lo pegamos en font1 o font2 o... en una nueva fuente y... eso es todo.
Ahora, si te parece complejo el cambio de fuente, puedes dejar la que hemos definido. Continuemos, entonces, con los últimos pasos de nuestra actividad.
Calificaciones. En dos textos presentaremos la nota acumulada y la nota final, así:
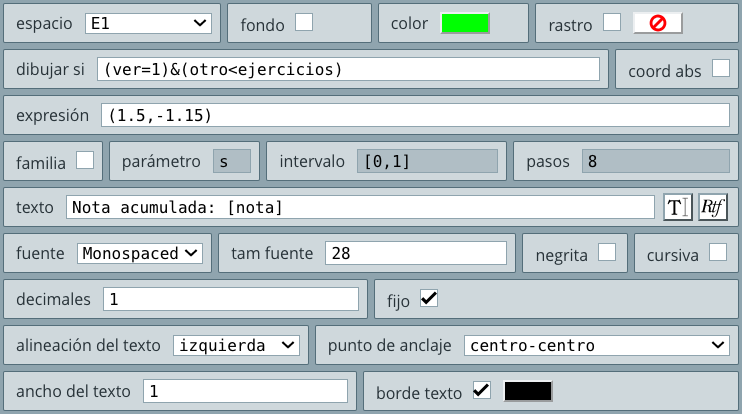
La diferencia entre uno y otro es la condición, para el primero se presentará una nota acumulada mientras aún falten ejercicios por realizar, el segundo texto presenta la nota final al no haber más ejercicios por realizar.
Mensaje de error. Texto que se muestra cuando hay piezas mal colocadas.
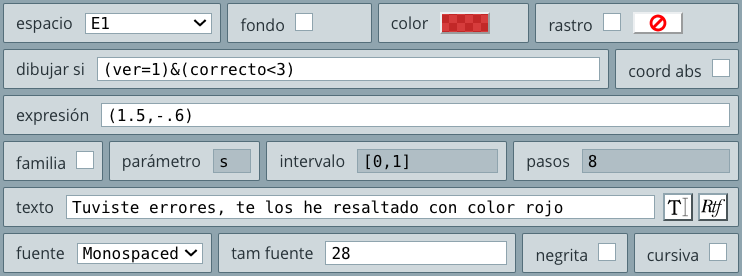
Este es un ejemplo de los textos que pueden aparecer:

Animación. Finalmente, incluimos una animación, la cual se invoca a través de un evento, cuya condición es que la variable anima sea uno (1). Esto siempre ocurrirá cuando hacemos clic en el botón Otro ejercicio.

El contenido del selector Animación es el que se muestra en la siguiente figura:
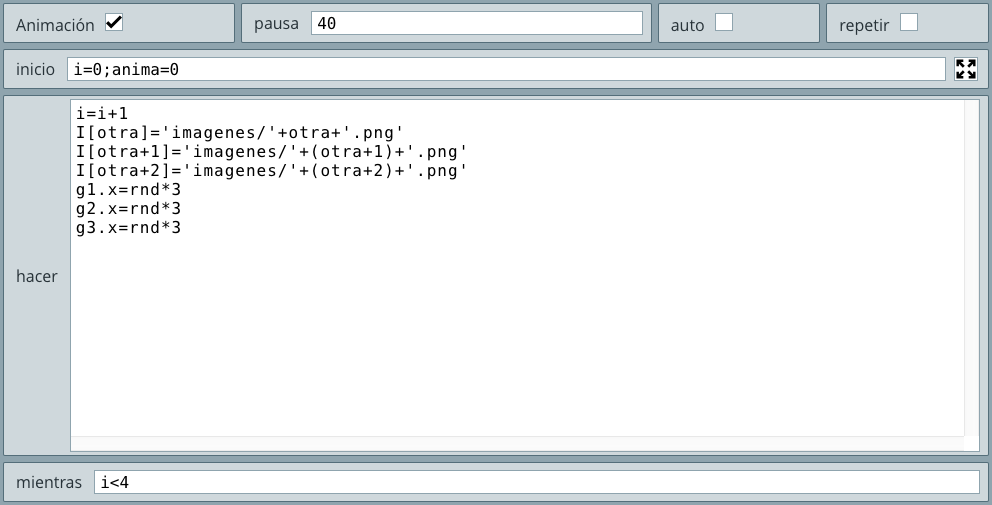
Se trata de un algoritmo tipo Do-While que se ejecuta cuatro veces. En cada ejecución se generan posiciones horizontales y aleatorias de los controles gráficos, se invoca, también, la función rota(). Estas ejecuciones tiene como efecto una animación en las imágenes cada vez que iniciamos un nuevo ejercicio.
El objetivo, entonces, es poner las imágenes en coordenadas aleatorias. Seguramente, habrás notado que el diseño de la actividad, antes de la animación, ponía las imágenes exactamente debajo de la posición correcta.
¡ESO ES TODO!
Utilizando la actividad anterior, haz los cambios necesario para diseñar un objeto interactivo de secuencias temporales de cinco contenedores. Una primera sugerencia, usa una escala de 150 para el espacio y en los polígonos un intervalo [0,4] y pasos = 4.
En las siguientes páginas, puedes observar secuencias temporales de 4 y 6 contenedores, descargada del proyecto Plantillas del Proyecto DescartesJS.
Hemos puesto una numeración a los contenedores, usando una familia de textos. También, hemos cambiado los fondos en cada de las dos escenas interactivas.
DescartesJS cuenta con muchas funciones y variables propias que evitan que el usuario tenga que programar las acciones más básicas. Es difícil tener en mente todas estas funciones y variables, por lo que se espera que este último capítulo funcione como una guía de rápido acceso a las funciones y variables intrínsecas de DescartesJS.
También se incluyen, cuando se considera importante, algunos ejercicios que agrupan el uso de algunas de estas funciones y variables.
DescartesJS tiene muchas variables asociadas a propiedades de los espacios, a acciones del ratón, a estatus de controles gráficos, etcétera. Estas variables pueden usarse tanto para conocer el estado de ciertas partes de un objeto interactivo (por ejemplo, el tamaño de un espacio), así como para modificar propiedades mismas del interactivo. A continuación se enuncian, en distintos apartados, dependiendo de la acción o la funcionalidad a la que pertenecen.
Las variables de espacio permiten conocer el alto, ancho y escala de un espacio. Adicionalmente, el usuario puede modificarlas para lograr espacios de características particulares. Las variables de espacio empiezan siempre con un prefijo que es el identificador del espacio en cuestión. Como notación usamos <Nombre del espacio>, para indicar que ahí va el identificador del espacio.
<Nombre del espacio>._w: Esta variable permite conocer el ancho de un espacio en pixeles. El sufijo w viene de width, que es anchura. Por ejemplo, la variable Esp._w nos permitiría conocer cuántos pixeles tiene de ancho el espacio Esp.
<Nombre del espacio>._h: Esta variable permite conocer el alto de un espacio en pixeles. El sufijo h viene de height, que es altura. Por ejemplo, la variable Esp._h nos permitiría conocer cuántos pixeles de altura tiene el espacio Esp.
<Nombre del espacio>.Ox: Esta variable permite conocer el desplazamiento horizontal del origen en pixeles. El sufijo Ox viene de offset de x. Por defecto, el origen del plano aparece en el centro del espacio. Pero se le puede asignar un desplazamiento (u offset) positivo si se desea moverlo a la derecha, o negativo si se quiere moverlo a la izquierda.
Esta variable sirve para conocer tanto el desplazamiento horizontal del origen, pero también se le puede asignar un valor si se quiere dar un desplazamiento horizontal. Es análoga a la variable que aparece como el campo de texto O.x en el selector Espacios cuando se tiene seleccionado el espacio en cuestión.
<Nombre del espacio>.Oy: Esta variable permite conocer el desplazamiento vertical del origen en pixeles. El sufijo Oy viene de offset de y. Por defecto, el origen del plano aparece en el centro del espacio. Pero se le puede asignar un desplazamiento (u offset) negativo si se desea moverlo hacia arriba, o positivo si se quiere moverlo hacia abajo.
Esta variable sirve para conocer tanto el desplazamiento horizontal del origen, pero también se le puede asignar un valor si se quiere dar un desplazamiento horizontal. Es análoga a la variable que aparece como el campo de texto O.y en el selector Espacios cuando se tiene seleccionado el espacio en cuestión.
<Nombre del espacio>.escala: Esta variable se usa para conocer la escala (el número de pixeles que hay entre una unidad y otra) del espacio. Por ejemplo, E7.escala es la variable asociada a la escala del espacio E7. También es posible asignarle un valor a dicha variable para forzar una escala especifica al espacio. Es análoga a la variable que aparece como el campo de texto escala en el selector Espacios cuando se tiene seleccionado el espacio en cuestión.
En el siguiente objeto interactivo puedes verificar algunas de estas variables:
Observa la configuración del control numérico, para la variable E2.escala. Los otros dos controles son análogos.
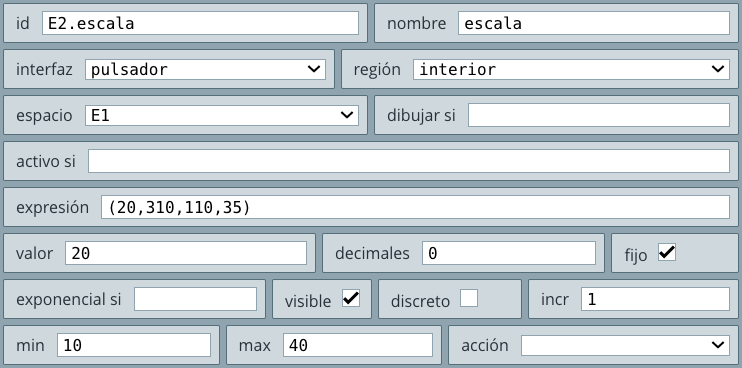
<Nombre del espacio>.rot.y: Esta variable sólo es válida para espacios tridimensionales. Guarda la rotación del espacio en grados alrededor del eje $y$. Por ejemplo, E2.rot.y sería la variable que guarda la rotación en grados alrededor del eje $y$ del espacio tridimensional E2.
<Nombre del espacio>.rot.z: Esta variable sólo es válida para espacios tridimensionales. Guarda la rotación del espacio en grados alrededor del eje $z$. Por ejemplo, E2.rot.z sería la variable que guarda la rotación en grados alrededor del eje $z$ del espacio tridimensional E2.
Es posible asignarle un valor a las dos variables anteriores, para forzar que el espacio al inicio tenga la perspectiva deseada. En el siguiente objeto interactivo puedes verificar el uso de las variables de espacio tridimensional:
Interactúa con el objeto y observa que puedes rotarlo o cambiar su escala, tanto de los controles como con los botones del ratón. Para algunos objetos interactivos de aprendizaje conviene, en ocasiones, fijar el espacio y dejar que las rotaciones se puedan hacer sólo desde los controles.
Las variables del mouse o ratón se usan para identificar el estado de este dispositivo; por ejemplo, si el botón izquierdo ha sido oprimido, o si está siendo oprimido. También se pueden conocer las coordenadas relativas del ratón. Para usar estas variables es preciso indicar el espacio relacionado (sobre el cual se quiere conocer el estado del ratón) mediante un prefijo, que es el identificador del espacio. Como notación usamos <Nombre del espacio> para indicar que ahí va el identificador del espacio.
<Nombre del espacio>.mouse_x: Esta variable permite conocer la coordenada horizontal relativa al plano cartesiano en que el mouse se encuentra al momento de estar presionado su botón. Su valor se refresca sólo cuando el mouse está oprimido (si el mouse sólo se pasea sin estar oprimido, el valor de esta variable no se refresca). Por ejemplo, la variable Esp.mouse_x nos indica la coordenada horizontal del mouse en el espacio Esp cuando se hace clic con el mismo.
<Nombre del espacio>.mouse_y: Esta variable permite conocer la coordenada vertical relativa al plano cartesiano en que el mouse se encuentra al momento de estar presionado su botón. Su valor se refresca sólo cuando el mouse está oprimido (si el mouse sólo se pasea sin estar oprimido, el valor de esta variable no se refresca). Por ejemplo, la variable Esp.mouse_y nos indica la coordenada vertical del mouse en el espacio Esp cuando se hace clic con el mismo.
Una forma de identificar las coordenadas del ratón, sin necesidad de apretar el botón, es activar en el espacio el checkbox sensible a los movimiento del ratón, tal como se aprecia en la siguiente figura:

Conocer las posiciones del ratón, en un espacio, es útil para el diseño de objetos interactivos de aprendizaje. En la siguiente escena, puedes evidenciar una aplicación en el plano cartesiano. Desplaza el ratón por cada cuadrante.
Veamos dos variables más para el ratón.
<Nombre del espacio>.mouse_clicked: Esta variable vale la unidad cuando el botón del mouse ha sido soltado tras por lo menos haber hecho clic una vez en el espacio en cuestión. Si el botón del mouse se oprime por primera vez y se mantiene oprimido, su valor es cero. Sólo se vuelve uno hasta soltar el botón mouse. Así pues, nos permite saber si el usuario ha hecho clic en un espacio o no, y siempre y cuando el botón del mouse ya haya sido soltado.
<Nombre del espacio>.mouse_pressed: Esta variable vale la unidad siempre que el botón izquierdo del mouse se encuentra oprimido. Si se suelta dicho botón, el valor de la variable regresa a cero.
Un ejemplo del uso de la variable <Nombre del espacio>.mouse_clicked, lo puedes ver en la siguiente escena interactiva.
Las variables de los controles gráficos se usan para conocer las coordenadas relativas de un control gráfico, así como para asignarle valores a las mismas. También nos permiten saber si un determinado control gráfico está siendo usado o no.
Para usar estas variables es preciso indicar el identificador del control gráfico (sobre el cual se quiere conocer información) mediante un prefijo, que es el identificador del mismo del control. Como notación usamos <Identificador del control> para indicar que ahí va el identificador del control gráfico.
<Identificador del control>.x: Esta variable se puede usar para imprimir el valor de la coordenada horizontal del control gráfico relativa al plano cartesiano. También es posible asignarle un valor a esta variable para colocar el control gráfico en una determinada posición horizontal.
Por ejemplo, la variable g1.x guarda el valor de la coordenada horizontal de un control gráfico con identificador g1.
<Identificador del control>.y: Esta variable se puede usar para imprimir el valor de la coordenada vertical del control gráfico relativa al plano cartesiano.
También es posible asignarle un valor a esta variable para colocar el control gráfico en una determinada posición vertical. Por ejemplo, la variable g1.y guarda el valor de la coordenada vertical de un control gráfico con identificador g1.
Estas dos variables las usamos en el diseño de las secuencias temporales.
<Identificador del control>.activo: Esta variable nos informa si un control está siendo usado o no. En caso afirmativo, su valor es 1 y de lo contrario es 0. Por ejemplo, la variable g1.activo nos indica si el control gráfico g1 está siendo usado o no. Un control gráfico está activo no sólo si el mouse se encuentra oprimido sobre él controlándolo. También se considera activo si se le hizo un clic y es el último objeto que se seleccionó. Es decir, si se hizo clic en el control gráfico, éste seguirá activo hasta que el mouse haga clic en otro lado distinto al control gráfico.
En los capítulo anteriores hemos trabajado con este variable, la cual es <identificador del control>.currentTime que, dándole un tiempo de argumento, posiciona la reproducción en el tiempo indicado del audio o video asociado al control. Igualmente, la usamos para determinar el tiempo de reproducción. Si se ha de mostrar como parte de un texto, es necesario tener activada una animación mientras se reproduce el audio o video puesto que la animación hace que constantemente se refresque el texto que muestra la variable.
rndEsta variable, cuyo nombre viene de random (o aleatorio) genera un valor aleatorio real entre 0 y 1 cada vez que es llamada. A veces se quiere tener un valor aleatorio entero definido en un determinado intervalo.
Para ello es necesario asociar la variable rnd con algunas funciones que nos permitan tener ese comportamiento.
Hagamos un breve ejercicio cuyo propósito es generar parábolas verticales de la forma $y = ax^2 + bx + c$, donde el coeficiente $a$ puede adoptar valores enteros entre -3 y 3 pero sin incluir el cero (si valiera cero, no se tendría una parábola sino una recta); el coeficiente $b$ puede adoptar valores enteros entre -4 y 4 incluyendo el 0; y $c$ puede adoptar valores reales entre 0 y 3.
Este ejercicio es muy ilustrativo en muchos aspectos, especialmente porque cada variable tiene una asignación distinta de valores. Cada vez que presionas el botón Parábola, se generan diferentes valores para a, b y c, de acuerdo a las siguientes instrucciones:
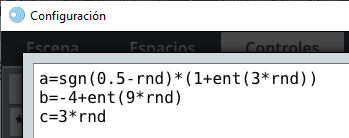
a primero extrae un signo de una expresión aleatoria y luego lo multiplica por otra expresión que es el valor entero aleatorio entre 1 y 3. Así, permite los valores -3, -2, -1, 1, 2 y 3 (excluyendo el 0). Nota que aunque hay dos distintos rnd en su asignación, cada uno lleva un valor aleatorio nuevo (no son el mismo valor).b, al no tener la restricción de no poder valer cero, se asigna como el valor -4 al que se le suma un valor aleatorio entero entre 0 y 8, de tal forma que puede adoptar valores entre -4 y +4.c, al no tener la restricción de ser entera, no requiere la función ent() que devuelve el valor entero de su argumento.rnd, en realidad, tiene su máximo en .99999. Se deja al usuario que analice cuidadosamente qué pasaría si ese máximo fuese uno (1). Considera la variable b: ¿Es probable obtener un valor de +4 para esta variable con la expresión dada?DescartesJS tiene una variedad de funciones propias, muchas de las cuales son las típicas utilizadas en casi cualquier lenguaje de programación. No obstante, adicionalmente tiene otras propias
relacionadas a audio, video, evaluación de funciones, etc. que se revisarán a continuación. Las funciones aquí presentadas se agrupan según su funcionalidad.
abs(): Es una función que recibe un argumento y devuelve el valor absoluto del mismo. Por ejemplo, abs(-2) devolverá 2.acos(): Es una función que recibe un argumento y devuelve su arcocoseno en radianes. Por ejemplo, acos(-1) devolverá el valor 3.141... radianes (que son 180°).asin(): Es una función que recibe un argumento y devuelve su arcoseno en radianes. Por ejemplo, asin(1) devolverá el valor 1.570... radianes (o 90°).atan(): Es una función que recibe un argumento y devuelve su arcotangente en radianes. Por ejemplo, atan(1) devolverá el valor 0.785... radianes (que son 45°).cos(): Es una función que recibe un argumento, lo interpreta en radianes, y devuelve el coseno del mismo. Por ejemplo, cos(pi/2) (recordamos que $\frac{π}{2}$ equivale a 90°) devolverá el valor 0.cot(): Es una función que recibe un argumento, lo interpreta en radianes, y devuelve la cotangente del mismo. Por ejemplo, cot(0.785398163) devolverá un valor cercano a 1 pues 0.785398163 radianes es cercano a 45°.csc(): Es una función que recibe un argumento, lo interpreta en radianes, y devuelve la cosecante del mismo. Por ejemplo, csc(pi/2) devolverá un valor de 1.ent(): Es una función que recibe un argumento y devuelve el valor del entero inmediatamente inferior. Por ejemplo, ent(-3.2) devolverá el valor -4.Esta variable se puede extender a una que redondea si al argumento se le suma 0.5. Por ejemplo, ent(3.78+0.5) devolverá el valor 4, que es lo mismo que redondear 3.78. Nota también que cuando el argumento es positivo, el valor devuelto consiste simplemente en truncar al mismo (recortarle los decimales).
exp(): Es una función que recibe un argumento y devuelve el valor de la exponencial neperiana del mismo. Por ejemplo, exp(2) devolverá el valor de $e^2$, que es 7.389...._índiceDe_(): Es una función que recibe dos argumentos de tipo cadena de texto. El primero es el texto principal. El segundo es un texto contenido en el primero. La función devuelve un entero que es el índice (contando el primer carácter del texto principal como el cero-ésimo) en el que empieza el texto contenido. Si no encuentra el texto contenido en el texto principal, devuelve un valor de -1. Por ejemplo, _índiceDe_('hola','ola') devolverá el valor 1.log(): es una función que recibe un argumento y devuelve el logaritmo neperiano del mismo. Por ejemplo, log(7.389056099) devolverá un valor cercano a 2, ya que $e^2 =$ 7.389056099...._letraEn_(): Es una función que recibe dos argumentos. El primero es una cadena de texto. El segundo es un entero que corresponde al índice de la letra (empezando a contar la primera letra como la cero-ésima) que devolverá la función. Por ejemplo, _letraEn_('hola',1) devolverá el texto 'o'._longitud_(): Es una función que recibe un argumento de una cadena de texto y devuelve la longitud en caracteres del mismo. Por ejemplo, _longitud_('hola') devolverá el valor 4.max(): es una función que recibe un par de argumentos numéricos y devuelve el que es mayor de ambos. Por ejemplo max(-6,-3.59) devolverá -3.59.min(): es una función que recibe un par de argumentos numéricos y devuelve el que es menor de ambos. Por ejemplo min(-7,-4.2) devolverá -7.raíz() o sqrt(): Es una función que recibe un argumento y devuelve la raíz cuadrada del mismo. sqrt viene de square root. Por ejemplo, raíz(9) o sqrt(9) devolverá el valor 3.sec(): Es una función que recibe un argumento, lo interpreta en radianes, y devuelve la secante del mismo. Por ejemplo, sec(pi) devolverá un valor de -1.sen() o sin(): Es una función que recibe un argumento, lo interpreta en radianes, y devuelve el seno del mismo. Por ejemplo, sen(pi/2) o sin(pi/2) (recordamos que $\frac{π}{2}$ equivale a 90°) devolverá el valor 1.sgn(): Es una función que recibe un argumento, y de ser éste positivo devuelve el valor +1. De ser el argumento negativo devuelve -1. Es decir, extrae sólo el signo del argumento. Por ejemplo, sgn(-3) devolverá el valor -1.sqr(): Es una función que recibe un argumento y devuelve su valor al cuadrado. Viene de la palabra square. Por ejemplo, sqr(3) devolverá el valor 9._subcadena_(): Es una función que recibe 3 argumentos. El primero es una cadena de texto, el segundo y tercero son enteros que corresponden a índices de los caracteres de la cadena, contando el primer carácter como el cero-ésimo. La función devuelve una cadena de texto que va del índice del segundo argumento (inclusivo) al índice del tercer argumento (exclusivo). Por ejemplo, _subcadena_('hola',1,3) devolverá la cadena 'ol'.tan(): Es una función que recibe un argumento, lo interpreta en radianes, y devuelve la tangente del mismo. Por ejemplo, tan(pi/4) (recordamos que $\frac{π}{4}$ equivale a 45°) devolverá el valor 1.Existen también funciones trigonométricas hiperbólicas (seno, coseno y tangente). Basta agregar una h al final de cada una (sinh(), cosh() y tanh()).
En la siguiente escena interactiva puedes ingresar algunas de la funciones anteriores y verificar el resultado.
Además de las funciones propias de DescartesJS, podemos definir todas las que queramos o necesitemos en un interactivo en particular, constituyéndose en extensiones o adiciones a las funciones incorporadas. En el capítulo sobre familias ya habíamos dispuesto un texto descriptivo de cómo incorporar o definir nuevas funciones, del cual recordamos:
Un ejemplo que presentamos de definición de función fue el Máximo Común Divisor. En este apartado, presentamos tres ejemplos adicionales, un poco más simples pero que te ayudan a comprender cómo es su funcionamiento.
En la siguiente escena interactiva, en el selector Definiciones, hemos definido dos funciones, así:

Esta es la escena interactiva:
También es posible definir funciones con dos o más variables. En la siguiente escena interactiva puedes observar dos funciones de varias variables con su respectiva imagen, que ilustra cómo se definieron:
En estos dos ejemplos sólo hemos usado una instrucción para cada función; sin embargo, como se enunció antes, es posible definir una función con varias instrucciones, para ello, tendremos que hacer uso de la opción algoritmo. Un primer ejemplo fue el cálculo del MCD, un segundo ejemplo es el cálculo del factorial de un número entero positivo, que explicaremos con más detalle a continuación.
En primer lugar, definimos la función factorial, así:

Como vamos a usar un algoritmo, hemos asignado a la función factorial la variable f, lo que significa que el cálculo que se haga en el algoritmo para f, será retornado a la función. En segundo lugar, restringiremos los valores del número n al que le calcularemos el factorial, el cual no puede ser negativo:

Observa que hemos activado el checkbox del algoritmo. En tercer lugar, inicializamos un contador i en cero y la variable f en uno (1):

Finalmente, en hacer hemos puesto dos asignaciones. La primera es el contador que tendrá valores de 1, 2, 3, ..., n (recuerda que la asignación i = i + 1 se realiza mientras, i<n).
La segunda asignación, para cada iteración, funcionará así (f = 1*1), (f = 1*2), (f = 2*3), ..., (f = f*n), obteniendo finalmente, el factorial de n.
Este valor de f es retornado a la función.
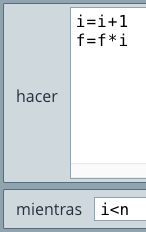
He aquí el objeto interactivo:
Para terminar, responde a $10$ preguntas planteadas en la siguiente escena interactiva. Puedes realizarla las veces que desees.
Te sugerimos realizar la prueba en una ventana ampliada.