Feliz Navidad y próspero y ¡saludable 2021!
Escrito por José R. Galo SánchezLa Red Educativa Digital Descartes os desea una Feliz Navidad y que el próximo año 2021 sea muchísimo más próspero que el actual y exponencialmente más saludable.
Compartimos con vosotros nuestra tradicional postal navideña interactiva para que sonriáis ¡seguro que lo haréis! y os entretengáis un poquito con nosotros. Pulsa sobre la siguiente imagen para acceder a ella.
Autor de la postal: Dr. Juan Guillermo Rivera Berrío, presidente de la RED Descartes de Colombia y vicerrector de la Institución Universitaria Pascual Bravo.
¡Felicidades a toda la comunidad educativa que interactúa, aprende y enseña usando los recursos interactivos de RED Descartes y que da sentido a nuestra labor altruista!
La Astrofísica es la rama de la ciencia que estudia las propiedades físicas de los cuerpos celestes, tales como luminosidad, tamaño, masa, temperatura y composición, así como su origen y evolución. Es decir, se preocupa y ocupa de nuestro entorno, de ése que día a día tenemos al alcance de la vista sin más que simplemente elevar la cabeza, observar nuestro cielo y fijarnos en lo que en él habita, y del que fácilmente, minuto a minuto, segundo a segundo, nos olvidamos, pues solemos preferir centrarnos en nuestra pequeñez cercana y no en la grandeza lejana. ¡Claro!, la cercanía nos hace creer que lo grande es lo próximo y lo pequeño lo lejano. Pero no es únicamente esta simple y errónea causa, ya que si cegador es tratar de observar nuestro cercano astro, el Sol, más abrumador es observar el cielo nocturno y quedarse deslumbrado por un incontable conjunto de objetos emisores de luz y de otros que los reflejan, junto a una sorprendente acumulación de sombras y claroscuros que han sido admirados desde los orígenes de nuestros tiempos y que mitológicamente se asimilaron a un cami no generado por la leche derramada por la diosa Hera: la Vía Láctea. Y ante todo ello, una mínima reflexión conduce a una obvia sensación de pequeñez personal que no es microcóspica —dado que esa medida sería muy grande—, sino que hemos de decir que es yoctométrica, ya que no hay prefijo indicador de menor tamaño, aunque siendo consecuentes deberíamos ubicarnos en la hipoyoctometría. Ante esa percepción, la reacción consecuente es abandonar rápidamente esa sensación de presión infinita y expandirse, cual big bang, regresando a la métrica en que volvemos a ser tangibles humanos, auto-encumbrados como reyes de la Naturaleza. Pero, afortunadamente, hay quienes son capaces de sobreponerse a su pequeñez, y sin abandonar la consciencia del mínimo tamaño que la Humanidad ocupa y de la ínfima sapiencia que alcanza, saben extender su mente —increíble y paradójicamente, ésta, sí es capaz de superar la yotta-realidad— y se adentran en caminos y vías que nuncan surcarán sus celulas, ni podrán ver sus limitados ojos, pero que contribuyen a introducir cierto orden y conocimiento en nuestro ser.
no generado por la leche derramada por la diosa Hera: la Vía Láctea. Y ante todo ello, una mínima reflexión conduce a una obvia sensación de pequeñez personal que no es microcóspica —dado que esa medida sería muy grande—, sino que hemos de decir que es yoctométrica, ya que no hay prefijo indicador de menor tamaño, aunque siendo consecuentes deberíamos ubicarnos en la hipoyoctometría. Ante esa percepción, la reacción consecuente es abandonar rápidamente esa sensación de presión infinita y expandirse, cual big bang, regresando a la métrica en que volvemos a ser tangibles humanos, auto-encumbrados como reyes de la Naturaleza. Pero, afortunadamente, hay quienes son capaces de sobreponerse a su pequeñez, y sin abandonar la consciencia del mínimo tamaño que la Humanidad ocupa y de la ínfima sapiencia que alcanza, saben extender su mente —increíble y paradójicamente, ésta, sí es capaz de superar la yotta-realidad— y se adentran en caminos y vías que nuncan surcarán sus celulas, ni podrán ver sus limitados ojos, pero que contribuyen a introducir cierto orden y conocimiento en nuestro ser.
Y en la línea antes esbozada, en este artículo divulgador, presentamos un recurso educativo interactivo desarrollado por nuestro socio, el profesor José Luis San Emeterio Peña, con el que logra adentrarnos en el mundo de la Astrofísica y nos ayuda a iniciarnos en el conocimiento actualmente existente sobre nuestro Universo. Él, al titular su recurso como "Unas gotas de Astrofísica", también acude a la contraposición literaria ya que nos traslada que con este objeto interactivo nos da acceso a unas pocas gotas, cinco, pero cada una de ellas actúa y es un inmenso agujero negro acumulador de saber. Pero será mejor que dejemos que sea el propio autor quien nos adentre en su recurso y para ello acudamos y transcribamos a continuación la introducción que realiza sobre el mismo y que resume como: "Una introducción fácil en temas un tanto difíciles":
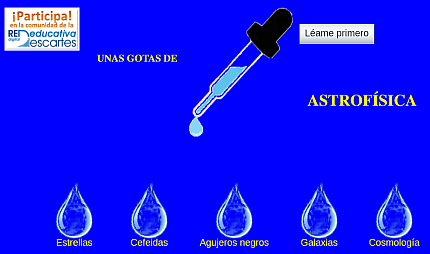
Si el usuario pulsa el botón “Léame primero” de esta unidad, verá que el propósito de su elaboración es mostrar algunos de los aspectos más notables de la Astrofísica sin necesidad de utilizar matemáticas avanzadas. Cualquier estudiante que haya superado un bachillerato de ciencias está bien cualificado para entender las explicaciones que se dan y cualquier ciudadano con curiosidad puede apreciar en las escenas interactivas aspectos de la realidad que quizás desconocía.
En cada “gota” se incluyen explicaciones teóricas de fácil comprensión y una propuesta de actividades para realizar con la escena correspondiente. Se incluyen cinco “gotas”:
- “Estrellas” aprovecha el estudio de un físico italiano, L. Zaninetti de la universidad de Turín, sobre el diagrama Hertzsprung-Rusell para que podamos examinar las propiedades concretas de muchas estrellas y reflexionar un poco sobre ellas.
- “Cefeidas” explica las propiedades de este peculiar tipo de estrella variable y nos guía para que podamos comprender su importancia como “aparato” de medida de las dimensiones cósmicas.
- Agujeros negros” está pensado para poder responder a algunas de las preguntas que suelen plantear sobre ellos los alumnos de segundo de bachillerato: ¿Por qué es peligroso acercarse a un agujero negro, aunque no penetremos en su interior? ¿Es cierto que el tiempo pasa de modo diferente en sus proximidades? ¿Se puede salir de un agujero negro?
- “Galaxias” contiene algunas explicaciones sobre la forma en que vemos la Vía Láctea y los diversos tipos de galaxias; pero, sobre todo, contiene también una escena particular, basada en un trabajo de PaulHellings en “Astrophysics with a PC”, con la que podemos comprender las diferentes formas de moverse una estrella en una galaxia como la nuestra.
- “Cosmología” contiene una pequeña explicación teórica que nos permite comprender la inestabilidad esencial del Universo y una escena donde podemos ver las diferentes posibilidades de evolución cósmica a partir de solo un par de parámetros.
No hay por qué seguir un orden determinado al “mojarse” con las diferentes “gotas”. Podemos introducirnos directamente en la que más curiosidad nos produzca.
Te animamos a mojarte y a aprender. Pulsa sobre la imagen para acceder al recurso:
Gracias a José Luis San Emeterio por proporcionarnos este cuentagotas con el que hemos podido limpiar y abrir nuestros ojos hacia ámbitos que son de difícil comprensión, pero que él ha logrado simplificar haciéndolo asequible a legos e inexpertos y dejando satisfechos a instruidos y expertos.
Proyecto de investigación en AJDA (II)
Escrito por Jesús Manuel Muñoz CalleLa línea de investigación del Proyecto AJDA llevada a cabo en colaboración con varios profesores del departamento de Ingeniería Telemática de la Escuela Técnica de Ingenieros Industriales de la Universidad de Sevilla sigue adelante.
En julio de 2020 se ha publicado el Trabajo Final de Grado titulado "Aplicación de gestión de juegos para la educación con framework Spring y Primefaces" y realizado por Ana María Lobón Roldán. En el mismo se ha desarrollado parte de una plataforma para la gestión y el uso de juegos del Proyecto AJDA.
Actualmente están en desarrollo nuevos TFG, continuación de los anteriores y cuyo principal objetivo es completar los trabajos ya desarrollados y obtener productos totalmente funcionales.
Además se trabaja en el Proyecto de Investigación "Estudio Integral del Impacto de la Gamificación Digital (GAIMS)" que pretende ahondar en la investigación científica y técnica de esta temática..
Planifica el curso académico 2020-2021 con el Proyecto AJDA
Escrito por Jesús Manuel Muñoz Calle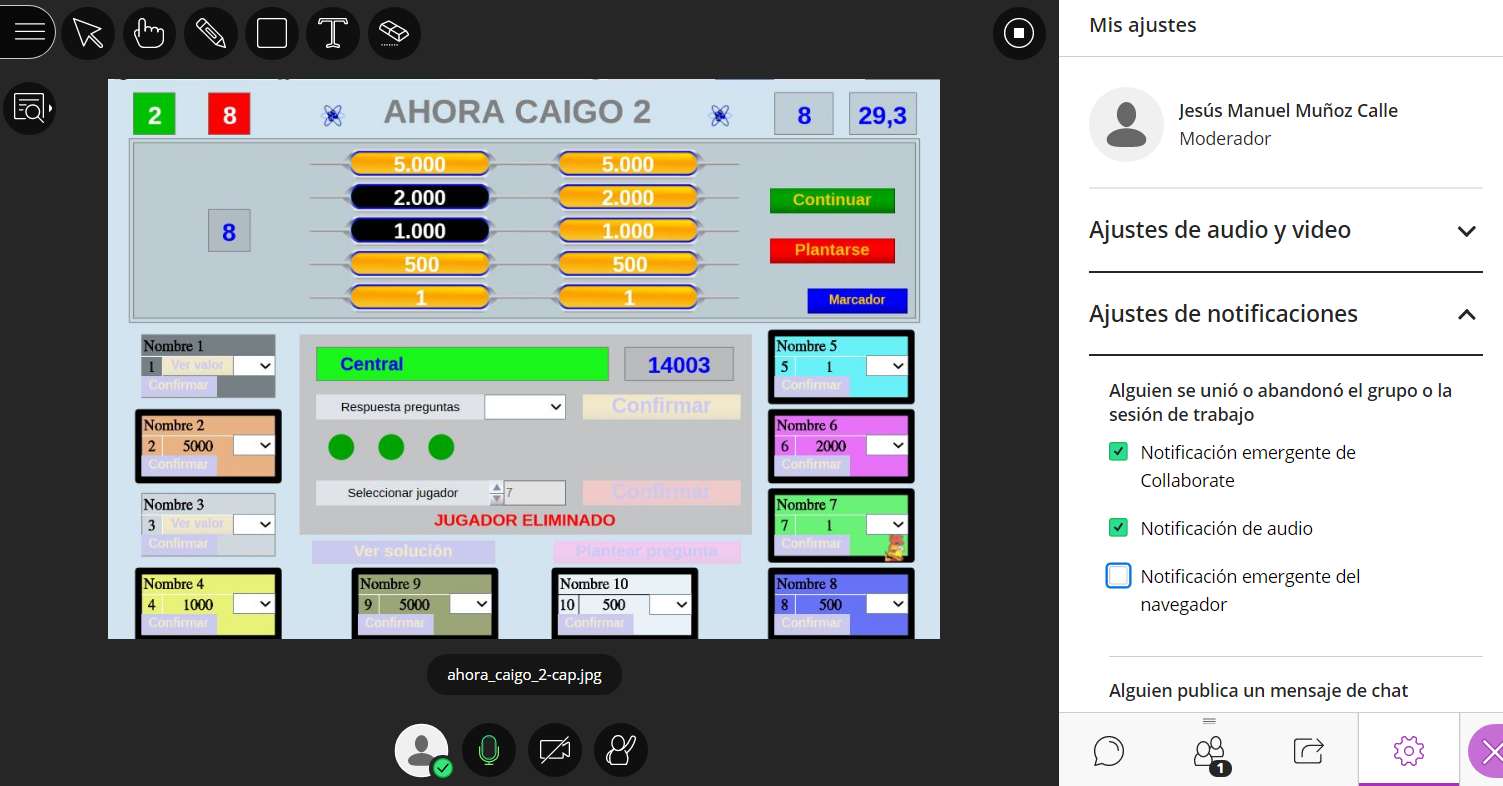
Planifica el nuevo curso escolar en la Universidad con Descartes
Escrito por Elena Álvarez SáizEn los últimos artículos publicados se han descrito distintos recursos del Proyecto Descartes que pueden servir para planificar el nuevo curso tanto en los niveles de infantil, primaria y secundaria como de bachillerato. En esta ocasión, nos centraremos en el nivel universitario, presentando ejemplos de algunos recursos digitales de la Red Descartes y destacando tres posibilidades para su incorporación en las asignaturas que impartimos. Dado que el próximo curso se presenta con muchas incertidumbres sobre la modalidad de impartición de la docencia, se requiere tener previsto una adaptación rápida a cualquier situación que se pueda producir por la evolución de la Covid-19. En función de cómo se presenten los acontecimientos, se podrá llegar a una reducción de presencialidad en el aula, total o parcialmente, y, con ello, habrá que tener previsto cómo realizar la adaptación de los materiales y recursos docentes que se pondrán a disposición de los estudiantes, así como de las metodologías a utilizar que resulten más adecuadas en cada momento.
Una de las opciones disponibles para incorporar materiales digitales en nuestro aula, y que nos facilita la Red Descartes, es la de convertirnos en creadores de contenidos. Para ello, la Red promueve la utilización de la herramienta DescartesJS, que permite diseñar y crear recursos multimedia interactivos para cualquier nivel educativo. Se pueden generar actividades o explicar contenidos incorporando gráficos, texto, animaciones, video, sonido e interactividad. La Red proporciona, además, documentación técnica y materiales para el autoaprendizaje y cuenta con el apoyo de todos sus miembros para resolver las dudas que puedan surgir durante la creación de estos recursos. Se puede obtener más información sobre DescartesJS en los siguientes enlaces:
- Información de la herramienta.
- Documentación técnica interactiva.
- Documentación técnica en PDF.
- Libros digitales de autoaprendizaje.
Otra de las opciones posibles de utilización de los recursos que proporciona la Red, tanto para el profesorado como para los estudiantes, es la posibilidad de incorporar, como parte de los materiales de uso docente, la gran cantidad de recursos digitales ya creados en los distintos subproyectos. Salvo que el material explicite lo contrario, en general, los recursos cuenta con una licencia Creative Commons (BY-NC-SA 4.0) lo que permite que puedan ser compartidos y adaptados en ciertas condiciones (atribución, uso no comercial y compartir igual). Por esta razón, se pueden incluir en blogs, páginas docentes, aulas virtuales o descargarse para uso personal. Los formatos van desde escenas aisladas, unidades didácticas hasta libros digitales interactivos.
De los subproyectos de la Red, que cuentan con material a nivel universitario, se encuentran los siguientes:
- Misceláneas. Unidades aisladas interactivas.
- Proyecto Un100. 100 unidades ejemplares que abordan una gran variedad de contenidos y que se estructuran a partir de una introducción, un desarrollo y un resumen de los contenidos.
- iCartesiLibri. Libros dinámicos, interactivos, multimedia, centrados en el aprendizaje y que facilitan el aprendizaje autónomo.
- Proyecto Ingeniería y Tecnología.Contenidos digitales que se encuadran en diferentes áreas de conocimiento y que en la mayoría de los currículos de programas de ingeniería o formación tecnológica
- Proyecto Prometeo. Escenas interactivas diseñadas para abordar temas principalmente de matemáticas y física,
- Aplicación de juegos didácticos en el aula.Juegos didácticos configurables adaptables a cualquier nivel y asignatura.
- Plantillas. Escenas configurables con documentación y vídeos en los que se detalla cómo utilizar las plantillas para desarrollar recursos.
- Problemas. Materiales para que el alumnado investigue, deduzca y llegue a conclusiones por sí mismo sobre contenidos diversos de Física y Química.
Estos recursos no se centran solo en contenidos matemáticos, sino que abarcan otras disciplinas: física, química, computación, etc. Para dar idea de la amplia variedad de contenidos ya desarrollados, se muestran algunos ejemplos en la presentación que se ha incorporado al final del artículo. Se invita a navegar por las distintas páginas que se citan y utilizar las herramientas de búsqueda para seleccionar aquellos que se ajusten a un interés concreto.
Por último, puede resultar de gran ayuda a la hora de planificar el curso próximo, conocer las experiencias en el aula que se han llevado a cabo por distintos miembros de la Red ya que pueden servir de inspiración a la hora de plantear actividades en nuestra propia práctica docente. A través de artículos publicados en el blog de la Red Descartes, se explica en detalle los objetivos perseguidos, la planificación realizada, las dificultades encontradas y los resultados obtenidos. Algunas de estas experiencias pueden consultarse en el siguiente enlace.
En la presentación siguiente, se muestran algunos ejemplos y las páginas de enlace a diversos materiales ya creados que pueden ser utilizados directamente o bien adaptarse con ayuda de la herramienta DescartesJS.
Planifica el nuevo curso escolar en Bachillerato con el Proyecto Descartes
Escrito por Ildefonso Fernández TrujilloPara este nuevo curso académico 2020 – 2021 el 'Proyecto Descartes' ofrece una amplia cantidad de objetos informáticos, dinámicos e interactivos de ayuda a la enseñanza y al aprendizaje de los contenidos curriculares de las diferentes asignaturas de Bachillerato.
Una de las características de la #REDDescartes es la continua atención a todo lo relacionado con las nuevas tecnologías y la educación de ahí que esté analizando ininterrumpidamente nuevas posibilidades didácticas en este ámbito. La mayor parte de los materiales didácticos de #REDDescartes lleva implícitas técnicas de autoformación y autoevaluación.
El interés actual que tiene para los usuarios del Proyecto Descartes queda perfectamente resumido en los siguientes enlaces: enlace 1 y enlace 2. Señalamos la particularidad de que en el último mes de Agosto se han servido más dos millones cien mil páginas.
El Proyecto Descartes ha creado recursos interactivos para PC, tablet y smartphone en las áreas de: Matemáticas, Lengua, Ciencias Naturales, Física y Química, Biología, Inglés, Francés, Artes Plásticas, Tecnología, Geografía, etc. Ver:
https://proyectodescartes.org/indexweb.php
En la página enlazada anteriormente se muestran todos los recursos disponibles hasta el momento del acceso. Se observa que los relativos a Bachillerato se encuentran en los subproyectos:
En algunos subproyectos no se menciona que contengan material para bachillerato pero los hemos añadido por considerar que parte de los recursos de dichos subproyectos son aplicables a la etapa.
Hemos hecho notar que la disponibilidad de materiales está actualizada hasta el momento del acceso debido a que, en la actualidad, el proceso de creación de nuevos recursos está experimentando un crecimiento extraordinario tanto en cantidad como en calidad y diversidad, lo que hace aconsejable revisar con cierta frecuencia el contenido de la página. En la actualidad se está adaptando el 'Proyecto Prometeo', abundante en contenidos con lo que el aporte de nuevo material es contínuo.
Si bien los libros del subproyecto iCartesiLibri son creaciones dinámicas e interactivas pensadas para usarse tal cual están, al igual que los recursos del resto de los subproyectos, es de señalar la posibilidad de adaptar fácilmente los contenidos de dichos recursos a las necesidades propias o a las características del aula, especialmente las Misceláneas que con un mínimo de cambios pueden convertirse en una herramienta propia que satisfaga nuestros criterios educativos y de aprendizaje. Todo lo que necesitamos para realizar los cambios en los recursos es el 'Editor Descartes' herramienta (editor) intuitiva y de fácil uso.
Una vez que se ha visto la estructura de un recurso y se ha hecho uso de él se intuye la facilidad para la creación de uno parecido para lo cual disponemos de tres libros interactivos en el subproyecto iCartesiLibri, 'Formación en DescartesJS', que detallan todas las funcionalidades y procedimientos del editor Descartes y también está disponible una documentación exhaustiva en línea.
Cada subproyecto y cada recurso del mismo disponen de la documentación necesaria para que fácilmente identifiquemos sus objetivos y las indicaciones necesarias para su uso.
Estamos hablando de los recursos digitales que podemos encontrar en el Proyecto Descartes y de planificación de un curso escolar en estado de pandemia donde es importante disponer de un método de trabajo que pueda facilitar la formación de alumnos cuando se dificulta o incluso se suprime la enseñanza presencial. Recomiendo el informe de la experiencia de nuestro compañero José Antonio Salgueiro, hábil usuario de las técnicas de comunicación, cuando en el curso pasado se vio obligado a cerrar su aula e interrumpir la enseñanza presencial con un grupo de alumnos. El resultado de su experiencia bien puede servir de inspiración al docente o al menos tenerlo en cuenta al hacer su propia planificación.
En su reciente artículo titulado "Evaluación, durante el estado de alarma, de la práctica docente a distancia con un modelo sin videoconferencia" nos dice
"En primer lugar, dejaremos constancia de que este artículo no se fundamenta en ningún trabajo de investigación educativa ni en una experimentación didáctica previamente planificada y diseñada con unos objetivos concretos, sino que pretende difundir entre el claustro virtual una experiencia surgida de la improvisación y compartir los recursos generados con la práctica docente a distancia y sin videoconferencia en la materia de Matemáticas-II del Bachillerato de Ciencias con el alumnado del IES Bajo Guadalquivir de Lebrija, por si fuera de utilidad para otros compañeros y compañeras."
Ildefonso Fernández Trujillo. 2020
Planifica el nuevo curso escolar en Infantil y Primaria con el Proyecto Descartes
Escrito por José Antonio Salgueiro GonzálezComenzamos el curso escolar más complicado y difícil de los últimos cincuenta años, un curso que ha generado enorme inquietud entre todos los sectores de la comunidad educativa, desde el profesorado, como así se observa en la intensa actividad desarrollada durante el mes de agosto en las redes sociales, pasando por las asociaciones de padres y madres, asociaciones de directores y directoras, sindicatos de la enseñanza e incluso alguna asociación del cuerpo de inspección educativa. También tenemos las declaraciones de un conocido juez de menores que lo ha descrito con pocas palabras: "Será lógico, pero yo no lo entiendo". Así que, durante el estado de alarma y el período vacacional que finaliza, hemos tenido que ser testigos de las acusaciones sobre grupos de jóvenes, calificados de irresponsables, al no respetar las medidas de seguridad establecidas por las autoridades sanitarias, entre ellas el distanciamiento físico. Sin embargo, parece ser que no se guardará ese distanciamiento en los centros educativos, es decir, en los centros de formación de los futuros ciudadanos y ciudadanas. Y, por si fuera poco, hemos tenido que soportar el intento de descrédito por parte de algún gobernante, que lo único que consigue con este tipo de actitudes es perder la autoridad.
A pesar de todo, los profesionales de la enseñanza siempre empezamos los cursos escolares con ilusión, entusiasmo y emoción, atributos que esperamos transmitir, como en años anteriores, a todos los agentes que intervienen en la educación. Por todo ello, ofrecemos el acceso gratuito a nuestros recursos para el personal docente, el alumnado y sus familias, unos recursos interactivos que han demostrado su gran utilidad tanto en la enseñanza presencial como en la enseñanza a distancia. Concretamente, en este artículo, que da comienzo a la campaña de "la vuelta al cole", ofrecemos para las etapas de Infantil y Primaria, completamente actualizado, el catálogo de recursos interactivos en HTML5 para cualquier ordenador y dispositivo móvil, con una clasificación por área o materia, esperando que desde cualquier lugar del mundo, a cualquier hora, sólos o acompañados, repercutan en una mejor formación competencial de nuestro alumnado.
En tu Planificación didácTICa ¡cuenta con el Proyecto Descartes!
Escrito por José R. Galo SánchezComienza un nuevo curso académico intensamente cargado, rebosante, desbordante de sensaciones, de inquietudes, de incertidumbres, de dudas, de desconfianzas, pero también de ilusiones y de esperanzas. Nada anormal, ¡todos los inicios de curso son así!, ¿verdad? Y como en todo amanecer, el sol surge con ambiguas luces matutinas que no permiten entrever con claridad ni lo que nos rodea, ni lo que se aproxima, y consecuentemente ello coadyuva a la generación de cavernarias sombras platónicas, pero la experiencia y lo que es más certero: el conocimiento y la ciencia, nos muestra y nos da certeza de lo que acontecerá: el sol periódicamente alumbrará nuestro existir.  E incluso, aunque haya nubes que, aglutinándose en densos conglomerados de oscuras gotas, logren mitigar su fulgor y consigan filtrar su luminosidad, en el horizonte el alba marcará con firmeza un nuevo día que difuminará las nocturnas tinieblas y que nos dará claridad, fuerza y vigor.
E incluso, aunque haya nubes que, aglutinándose en densos conglomerados de oscuras gotas, logren mitigar su fulgor y consigan filtrar su luminosidad, en el horizonte el alba marcará con firmeza un nuevo día que difuminará las nocturnas tinieblas y que nos dará claridad, fuerza y vigor.
Sí, soy consciente, que posiblemente estés pensando dejar de leer este artículo, pues puede que no estés para interpretaciones o imágenes poéticas cuando lo que observas sobre ti son extensos nubarrones y oyes y sientes las vibraciones de los truenos que anuncian una muy próxima tormenta, pero te comento que tú y yo estamos en el mismo lugar, en análoga aula docente, es decir, bajo el mismo cielo y recibiremos el mismo aguacero. Sé, sin duda, que la lluvia calará nuestros cuerpos, pero como aprendiz de científico seguiré aferrándome a la Ciencia, y obviaré todos los mensajes con los que nuestros administradores-gobernantes y pseudo-científicos oficiales quieren mostrarnos una fantasiosa #VueltaSegura, porque me niego a que nos hagan dudar de qué es la verdad científica, por mucho que reiteradamente transmitan una nueva verdad que pendula a su conveniencia y a la que quieren vendernos cual elixir de buhonero. Y por ello, pienso que, he de empecinarme aún más y hacer hincapié en formar a mi alumnado como personas críticas capaces de colaborar y liderar acciones conducentes a escenarios éticos y solidarios, de verdadera Justicia Social, ¡qué sepan distinguir nítidamente las sombras de la luz! y eviten que aparezcan ilusionistas que con un único interés finalista propio sean capaces de producir esas engañosas penumbras.
Así pues, para conseguir ese objetivo y en este contexto y circunstancias, y obviando aquí lo relativo al cumplimiento de las condiciones sanitarias y laborales legalmente establecidas y que revindicaré en todo momento en los foros adecuados, he de centrarme en analizar la necesidad docente de estar preparado para los diferentes escenarios posibles y, para ello, contar con una "Planificación didácTICa" acorde a las necesidades de cada situación. Y, aunque es gramaticalmente incorrecto, he destacado en la palabra didáctica lo de "TIC" porque hablan de presencialidad, pero con la boca pequeña le añaden con voz queda el prefijo "semi" y parece ser que abordan compras e inversiones en hard ware y plataformas "educativas" con las que aparentar que ellos son los que cubren todo lo que el profesorado tuvo que gestionar motu proprio cuando en el mes de marzo quedamos desamparados. Pero no es aquello lo que me motiva, pues esto de las TIC es lo usual, básico e intrínseco en el proyecto Descartes, y es en lo que llevamos trabajando desde hace 22 años, ¡sí, veintidós años! Ahora parece que esto es nuevo, pero realmente no sería nada más que un redescubrimiento, una vuelta a la invención de la rueda, pues desde el proyecto Descartes se han desarrollado y hemos llevado a buen término programas educativos que han sido olvidados o que han sido tan hábilmente enterrados que parecen que son meros acontecimientos oníricos, por ejemplo: ¿qué se programó sobre centros TIC en Andalucía (el 2x1 o dos alumnos por ordenador)? o ¿qué era eso del Programa Escuela 2.0 y el 1x1? En el año 2005 se inició la "Experimentación con Descartes en el Aula" promovido por el INTEF, organismo del Ministerio de Educación, y hasta el 2010 se abordaron experiencias formativas en el proyecto EDA (Experimentación didácTICa en el aula) que dieron lugar a redes sociales de profesorado (ahora eso de red social suena habitual, pero todo tuvo su principio) como el proyecto HEDA y educ@conTIC. Y cuando desde los organismos oficiales decidieron dejar de apoyar proyectos de profesorado como el proyecto Descartes no dudamos y constituimos la ong "Red Educativa Digital Descartes" para preservar toda esa experiencia adquirida, canalizarla adecuadamente y potenciar el uso de las TIC en el proceso de enseñanza-aprendizaje.
ware y plataformas "educativas" con las que aparentar que ellos son los que cubren todo lo que el profesorado tuvo que gestionar motu proprio cuando en el mes de marzo quedamos desamparados. Pero no es aquello lo que me motiva, pues esto de las TIC es lo usual, básico e intrínseco en el proyecto Descartes, y es en lo que llevamos trabajando desde hace 22 años, ¡sí, veintidós años! Ahora parece que esto es nuevo, pero realmente no sería nada más que un redescubrimiento, una vuelta a la invención de la rueda, pues desde el proyecto Descartes se han desarrollado y hemos llevado a buen término programas educativos que han sido olvidados o que han sido tan hábilmente enterrados que parecen que son meros acontecimientos oníricos, por ejemplo: ¿qué se programó sobre centros TIC en Andalucía (el 2x1 o dos alumnos por ordenador)? o ¿qué era eso del Programa Escuela 2.0 y el 1x1? En el año 2005 se inició la "Experimentación con Descartes en el Aula" promovido por el INTEF, organismo del Ministerio de Educación, y hasta el 2010 se abordaron experiencias formativas en el proyecto EDA (Experimentación didácTICa en el aula) que dieron lugar a redes sociales de profesorado (ahora eso de red social suena habitual, pero todo tuvo su principio) como el proyecto HEDA y educ@conTIC. Y cuando desde los organismos oficiales decidieron dejar de apoyar proyectos de profesorado como el proyecto Descartes no dudamos y constituimos la ong "Red Educativa Digital Descartes" para preservar toda esa experiencia adquirida, canalizarla adecuadamente y potenciar el uso de las TIC en el proceso de enseñanza-aprendizaje.

Gracias a ello durante el confinamiento pudimos ayudar a numerosos colegas y alumnos en su labor docente y discente. Así, con sabor agridulce, superamos los cuatro millones de páginas en marzo, en abril ¡ayudamos en los tiempos del COVID-19! con más de cuatro millones seiscientas mil y en junio, coincidiendo con nuestro aniversario, comunicamos nuestro nuevo récord al haber superado los cinco millones de páginas servidas en el mes de mayo.
Por tanto estimo que desde el proyecto Descartes hemos contribuido a la educación con TIC tanto presencial como a distancia, también lo haremos en este nuevo invento de la semipresencialidad, y consecuentemente considero que los recursos educativos que ponemos a tu disposición con licencia Creative Commons pueden servirte en tu planificación docente. Son recursos que fomentan la autonomía del aprendizaje gracias a la interactividad, con ejercicios tipo que usan semillas aleatorias y cuentan con corrección automática. Nuestro objetivo es ayudar, ahora y siempre, a todo discente y docente en la planificación de su proceso de enseñanza y aprendizaje y aquí, en nuestro servidor de contenidos, con seguridad encontrarás ayuda y colaboración. Y, por ello, como indicaba en el título: En tu planificación didácTICa ¡cuenta con proyecto Descartes!
En posteriores artículos que iremos publicando sucesivamente en este blog, con ánimo de aportar una ayuda descriptiva adicional, os iremos detallando por niveles educativos los diferentes subproyectos que hemos ido desarrollando durante estos veintidós años. ¡Queda atento!
El metro: patrón inexacto para medir exactamente
Escrito por José R. Galo Sánchez"El metro: patrón inexacto para medir exactamente" es el título de un proyecto que desarrollamos en el año 2006 y cuya temática giraba en torno al patrón de longitud en el sistema métrico decimal: "el metro". Comprendía 50 objetos de aprendizaje, 117 escenas interactivas y 50 test también interactivos, todo desarrollado con la versión 3 de la herramienta Descartes que, recordemos, tenía como soporte la máquina virtual de Java. La adaptación al estándar HTML5 condujo en el 2013 a iniciar el desarrollo en javascript de DescartesJS y a la conversión y adaptación de las escenas de Descartes en Java a la nueva versión. El proyecto "El metro" quedó pendiente de esa adaptación y ahora, a través de este artículo, procedemos a presentarla.
 |
 |
Sí, hemos tardado en abordar esta adaptación, pero es evidente que no hay tiempo para todo y además cualquiera puede reconocer que una adaptación siempre es menos satisfactoria que un nuevo desarrollo y que a veces es más eficaz hacer que rehacer. También obliga a tomar decisiones sobre mantener lo que se hizo, con los estándares y limitaciones existentes en su momento, o remodelar totalmente, o quedarse entre Pinto y Valdemoro. La decisión final adoptada ha sido mixta:
- Por un lado se ha dado libertad a cada uno de esos objetos readaptándolos como misceláneas independientes, es decir, siguiendo el formato de presentación que se utiliza en ese subproyecto de RED Descartes y así, de esta manera, han pasado a estar disponibles sin necesidad de acceder a través del núcleo agregador que representa el proyecto.
- Pero también, por otro lado, para recordar y comprender cómo fue ese proyecto se ha mantenido el acceso original a través del índice y las páginas web auxiliares que aglutinaban a esos recursos y que detallaban su conceptuación y desarrollo, obviamente actualizando aquellos aspectos modificados.
En el proyecto misceláneas y en el servidor de contenidos ya están disponibles lo objetos adaptados, que todavía no son todos, y con este artículo se busca la divulgación de la web adaptada del proyecto. Al pulsar sobre la siguiente imagen tendremos acceso a la portada e índice del mismo.
 Pulsa sobre la imagen para acceder al proyecto
Pulsa sobre la imagen para acceder al proyecto
En la portada se muestra una suscinta galería de personajes
 |
 |
Y pulsando sobre las imágenes de cada uno de ellos, en dicha galería, accedemos a su respectiva biografía:
Jorge Juan y Antonio de Ulloa, junto a los franceses Bouguer, Godín y La Condamine, como medidores de la longitud del grado de meridiano en el ecuador y que junto a la medición del grado en Laponia, realizada por Maupertuis, permitió verificar que la Tierra estaba achatada por los polos. Un trabajo previo e independiente del sustentador de la definición del metro, pero con base técnica común: la triangulación geodesica.- Méchain y Delambre que abordaron la medición del meridiano desde Dunkerque (latitud 51 N) a Barcelona (latitud 41 N). Se seleccionaron esas ciudades por estar ubicadas en un arco que podía ser medido al ser accesible mediante desplazamiento sobre el terreno y por ser un arco ubicado en la parte intermedia del cuadrante. De esa medición se pasaría a la extrapolación de la medida del cuadrante de meridiano y a la definición del metro.
- Agustín de Pedrayes como representante español en el establecimiento del sistema métrico decimal.
- Méchain y Aragó que en una segunda expedición extendieron la medición del meridiano desde Barcelona a Formentera (latitud 38 N).
Os invitamos a navegar por las páginas enlazadas en el índice del proyecto y desde ellas profundizar en el planteamiento del proyecto, leer cuáles eran los objetivos y qué contenidos fueron los desarrollados. El proyecto era más amplio y ambicioso en alcance de lo que finalmente se realizó, pero hubo que poner cota a nuestros deseos, más cuando era un proyecto sometido a unos plazos y compromisos administrativos al haber sido seleccionado y subvencionado en convocatoria pública por la Consejería de Educación de la Junta de Andalucía en el año 2005.
De todas las opciones disponibles en el índice destacamos aquí, dentro de la descripción del proyecto: la motivación y los objetivos.
Y, obviamente, el repositorio o índice de contenidos donde hay que señalar que los iconos identificadores de los objetos que se observan en tonos de grises son objetos pendientes de adaptar y los coloreados ya han sido adaptados.
Es bien conocida la variabilidad continua y la amplia caducidad de la información que circula por la red y el peligro de pérdida de información en el que continuamente nos vemos involucrados por la simple variación en una página web o por su eliminación o bien por reiterados cambios de formatos y dispositivos que rápidamente van quedando obsoletos. Afortunadamente, hay grandes proyectos como Internet Archive que persiguen contrarrestarlo y hacer que lo efímero sea durarero. Aquí, en una línea paralela muy modesta hemos tratado de dar un poquito más de perdurabibilidad a nuestro proyecto de "El metro" dentro de la RED Descartes.
En vacaciones, invita a tu hijo o hija a explorar y pensar con Descartes
Escrito por José Antonio Salgueiro GonzálezLa pandemia que nos asola desde marzo originó la declaración del estado de alarma, el cierre de los centros educativos y nos llevó al confinamiento en nuestros domicilios, afectando a todos los sectores de la comunidad educativa y debiendo afrontar retos para los que ninguno contaba con experiencia. Por su parte, las administraciones educativas instaron a los centros a adoptar las medidas necesarias para continuar con el proceso de enseñanza-aprendizaje a distancia usando espacios virtuales y herramientas de intercomunicación, pero se precisaban recursos especialmente diseñados para la enseñanza a distancia. Por ello, el domingo 15 de marzo, publicamos y difundimos por nuestras redes sociales el artículo "Educación a distancia y gratuita con Descartes", en el que ofrecíamos, debidamente catalogados por etapas educativas, todos los recursos educativos abiertos de RED Descartes. Pues bien, cuatro meses después, y con un final de trimestre agotador para todos los sectores de la comunidad educativa, ponemos en marcha la campaña "Vacaciones con Descartes para las familias", donde sugerimos a padres y madres que inviten a sus hijos e hijas, en los momentos que consideren adecuados y en función de la edad, a explorar y pensar, conscientes del considerable número de familias que demandan los tradicionales cuadernos de vacaciones y que podrán personalizar con una sencilla selección de nuestros recursos gratuitos.
Nuestros niños y niñas se encuentran disfrutando del período vacacional de verano, con mucho tiempo para compartir con sus familias y amigos, así como para el descanso y ocio. No obstante, siempre es recomendable encontrar el momento adecuado para sugerirles una interesante lectura y realizar, en nuestra compañía o junto a sus hermanas y hermanos mayores, algunas actividades de las áreas básicas del conocimiento. Ahora bien, para ello, las familias requieren de una orientación y asesoramiento que pueden recibir por diferentes canales de comunicación.
Con este fin, la Red Educativa Digital Descartes ofrece una amplia selección de recursos digitales interactivos a los que pueden accederse desde cualquier lugar y hora, en el campo o en la playa, con un simple ordenador personal, portátil o dispositivo móvil y conexión a la red de internet, aunque también es posible descargarse el objeto de aprendizaje para usarlo en local, es decir, sin conexión a internet.
Estos recursos están organizados y catalogados por etapa educativa y edad, como se aprecia en la imagen inferior, así , las familias podrán seleccionar, con un simple clic sobre la imagen correspondiente o sobre el texto que la acompaña a su derecha, los adecuados para sus hijos e hijas, encontrando la relación con los nombres de las actividades y una breve descripción de la misma.
No obstante lo anterior, cada familia, como mejor conocedora de las capacidades de los niños y niñas, podrá optar por realizar las actividades de diferente edad.
La LOMCE no contempla los tres ciclos de Primaria, sino seis cursos independientes. lo que no supone obstáculo alguno para que los niños y niñas disfruten con estos recursos de gran calidad, pues accediendo al ciclo en cuestión, según la edad, y seleccionando el recurso deseado puede verse con detalle a qué curso concreto corresponde.
Esperamos que esta aportación, completamente gratuita, de la RED Descartes sea de utilidad para el mayor número posible de familias y animamos a dejar comentarios con sus opiniones.
El mapeado de la imagen se ha realizado desde la nube con la herramienta Image-Maps.
La Organización No Gubernamental RED Descartes viene ofreciendo, desde hace casi siete años, recursos educativos abiertos para todas las etapas educativas durante 24 horas al día y los 365 días del año, de forma completamente altruista, queriendo aportar nuestro granito de arena en estos tiempos tan difíciles. Por ello, elaboramos y difundimos este especial artículo veraniego con resumen y acceso a todos los recursos disponibles.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)






















 CONTACTO
CONTACTO
