La rotación de Rodrigues es un procedimiento analítico matricial, fácil y cómodo que permite rotar, un ángulo θ, un vector v tridimensional alrededor de otro vector unitario k = (k_x, k_y, k_z). La expresión matricial de este giro es la siguiente:

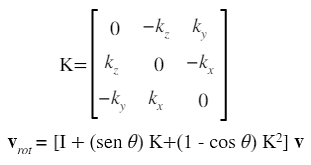
Su deducción puede realizarse mediante planteamientos vectoriales geométricos como se aborda en este artículo o bien apoyándose en el trabajo con cuaterniones. Este trabajo de Rodrigues ha quedado algo relegado y opacado por los ángulos de Euler o más directamente por los parámetros de Euler mediante los que se obtiene la fórmula de Euler-Rodrigues que no es más que una parametrización especial de la fórmula de Rodrigues reflejada anteriormente.

En este artículo se busca mostrar la aplicación de esta rotación de Rodrigues visualizando gráficamente su efecto y, en particular, usando la rotación dar respuesta al problema de obtener el desarrollo plano de las caras que determinan un ángulo poliedro. Esto último lo utilizaremos, a modo de ejemplo, para mostrar el desarrollo plano animado de un icosaedro, así como el de cualquier cilindro generalizado.

En la siguiente escena interactiva se tiene acceso a siete opciones de menú que detallamos a continuación.

Pulsa sobre la imagen para abrir la escena

• Matriz de rotación de Rodrigues: A partir de los datos aportados por defecto o de los introducidos por el usuario en los que se especifican las componentes del vector v que se desea a girar respecto al vector w, se calcula la matriz de rotación de Rodrigues para cada ángulo de giro aportado y se refleja gráficamente el movimiento indicado.
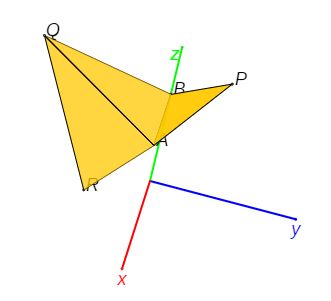
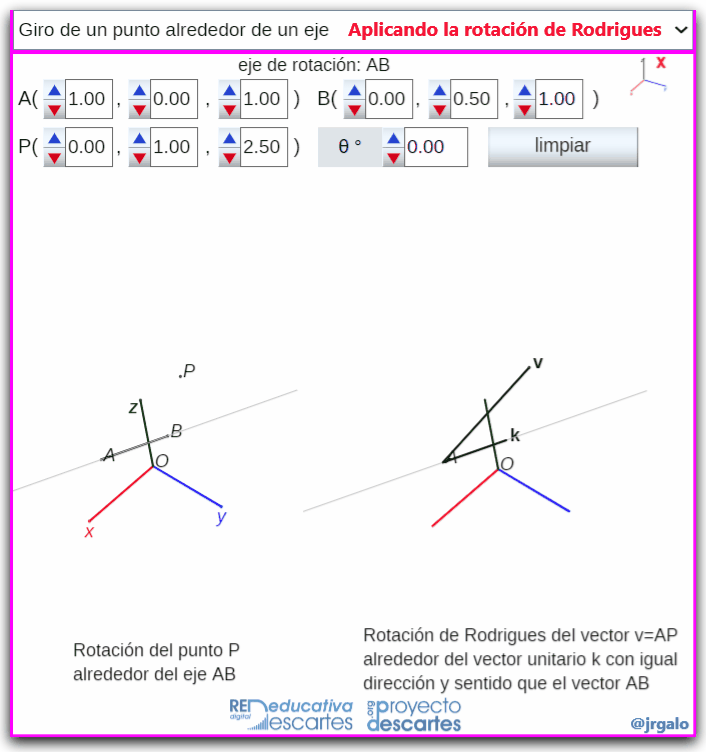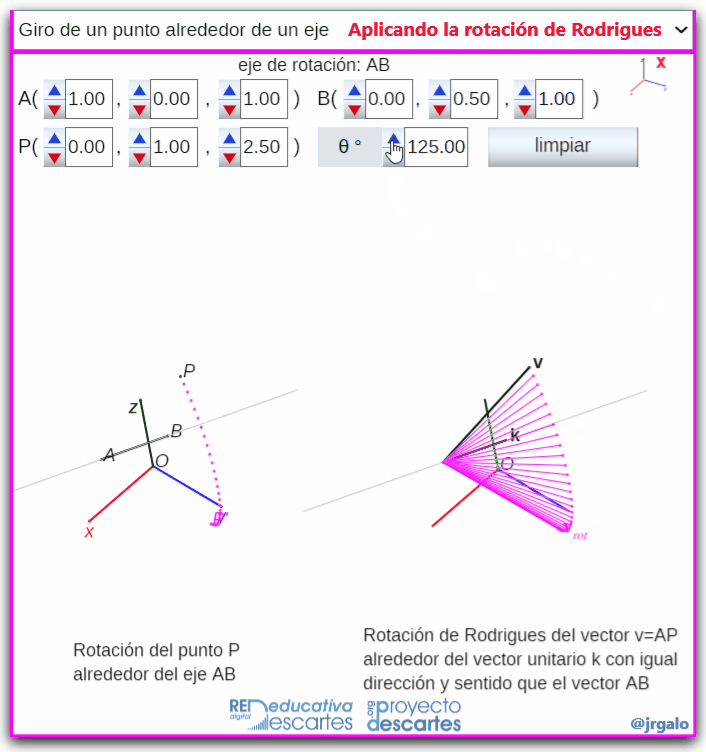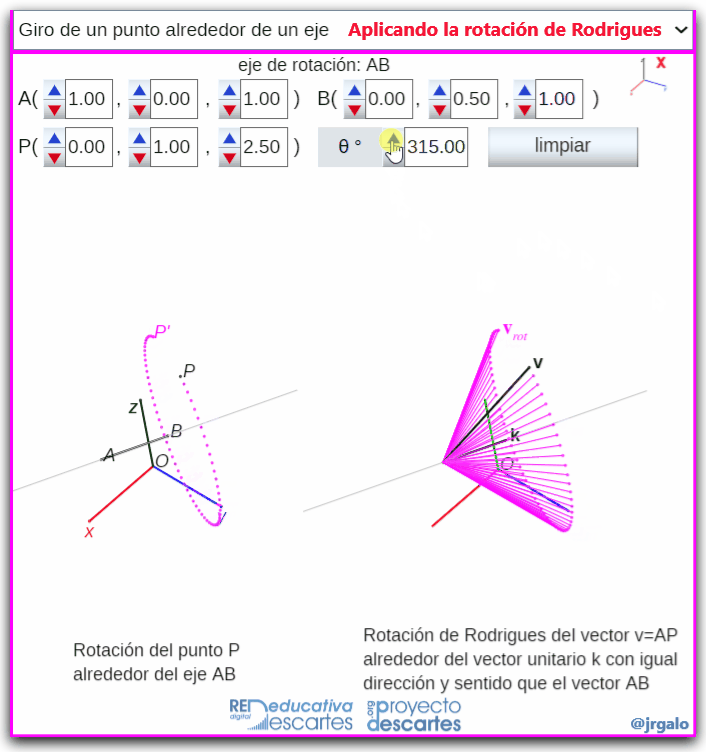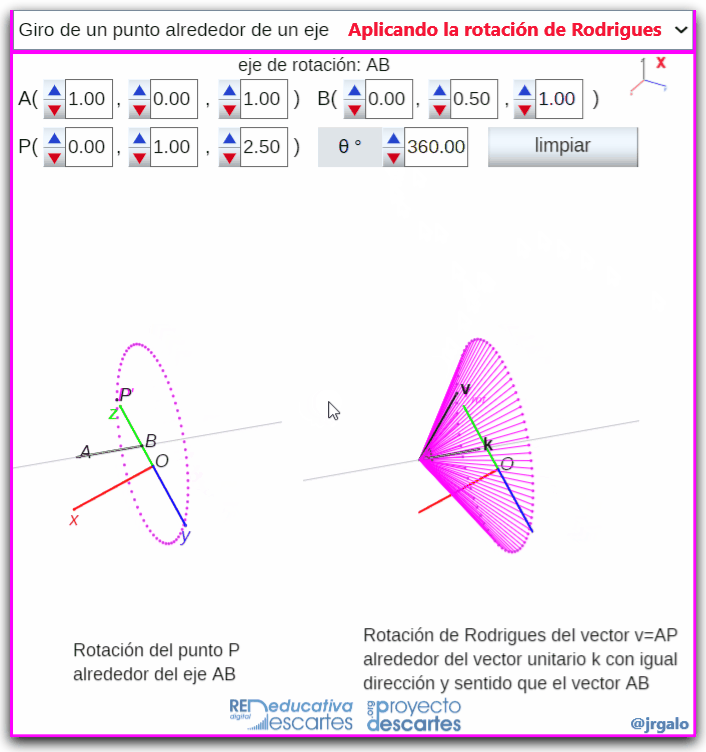
• Giro de un punto alrededor de un eje: Se plantea el problema geométrico de girar un punto alredor de un eje y éste se redefine como el problema vectorial analizado en el punto anterior.
  

  

  Pulsa sobre la imagen para ampliarla

• Giro manual de un triángulo alrededor de uno de sus lados: La situación se corresponde con el apartado anterior porque se reduce a girar el vértice del triángulo no perteneciente al lado alrededor del que se gira y este apartado servirá como primer paso para proceder al desarrollo plano antes anunciado. Se indica "giro manual" porque es el usuario el que indica manualmente el ángulo que desea que gire dicho triángulo. 
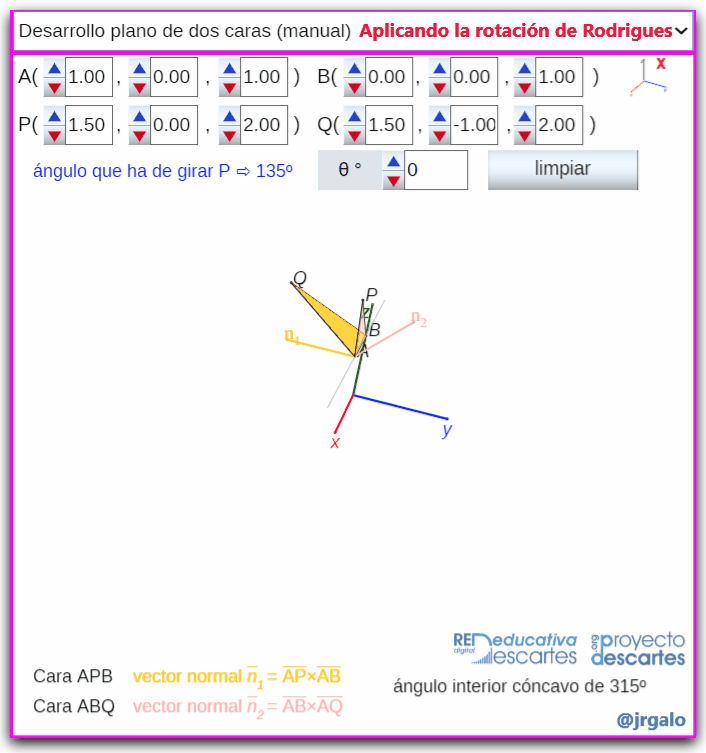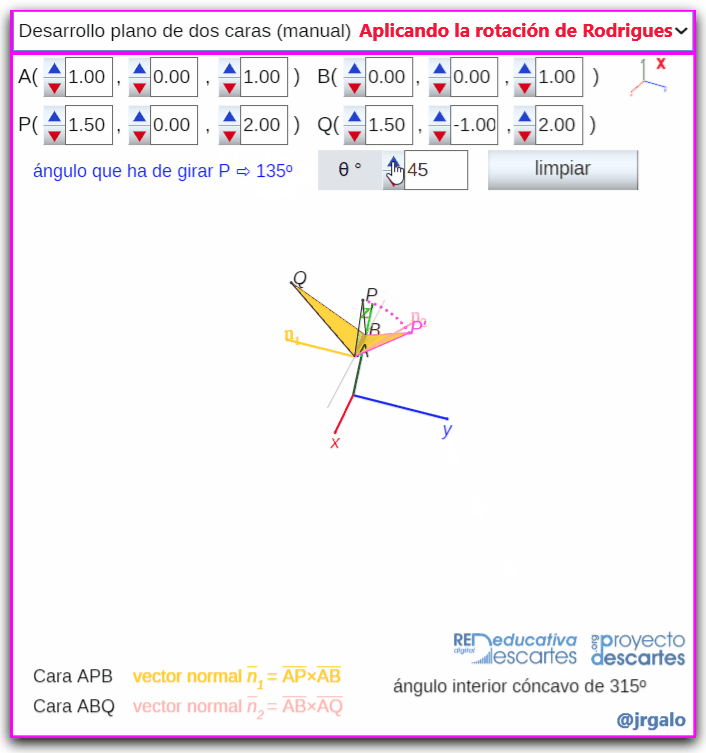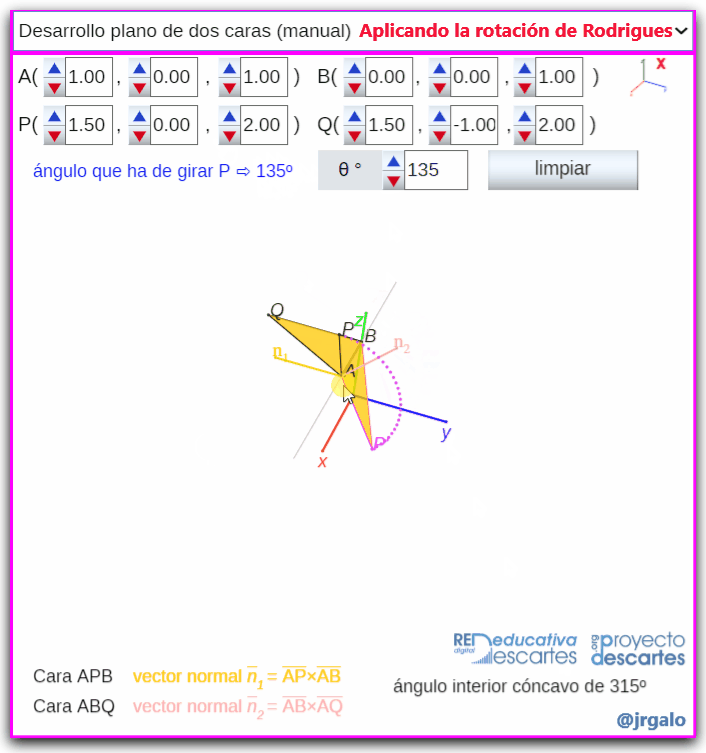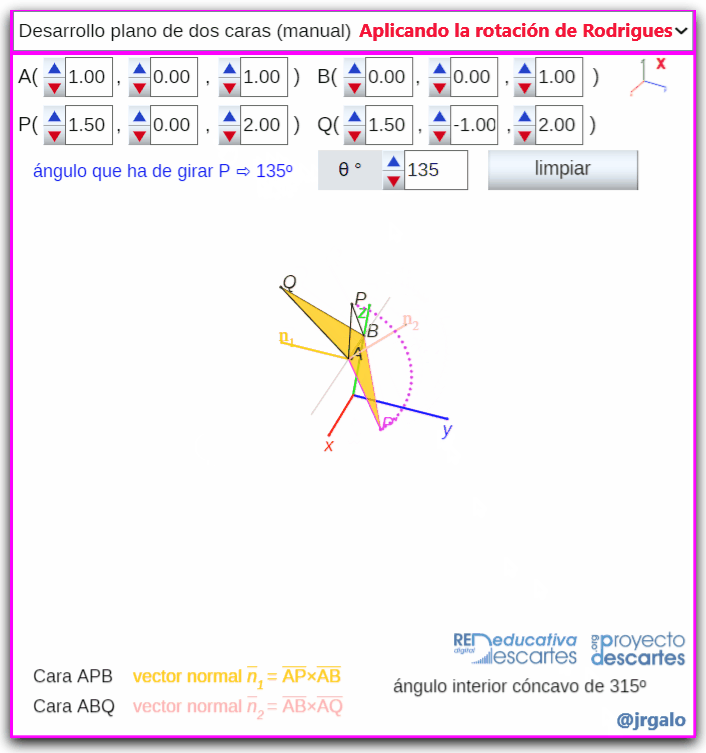
• Desarrollo plano de dos caras (manual): A partir de dos caras triangulares que comparten un lado se aborda el giro de una de ellas hasta hacer que ambas se ubiquen en un mismo plano, es decir, se aborda el desarrollo plano de un diedro. La situación se corresponde con el punto anterior y en este caso, aunque el giro se realiza manualmente, se indica cual es el ángulo que ha de girarse para conseguir el desarrollo plano buscado. Para calcular automáticamente este ángulo se determinan los vectores normales exteriores a dichas caras y el ángulo que foman ambos, y para determinar si el ángulo diedro interior es cóncavo o convexo se comprueba si el vector normal a los anteriores tiene el mismo sentido o no que el vector director del lado sobre el que se gira.
  

  

  Pulsa sobre la imagen para ampliarla

• Desarrollo plano de dos caras (automático): En esta opción se introduce una animación mediante la que se aborda de manera automática la obtención del desarrollo plano deseado. Obviamente es imprescindible la determinación automática del ángulo que ha de girarse.
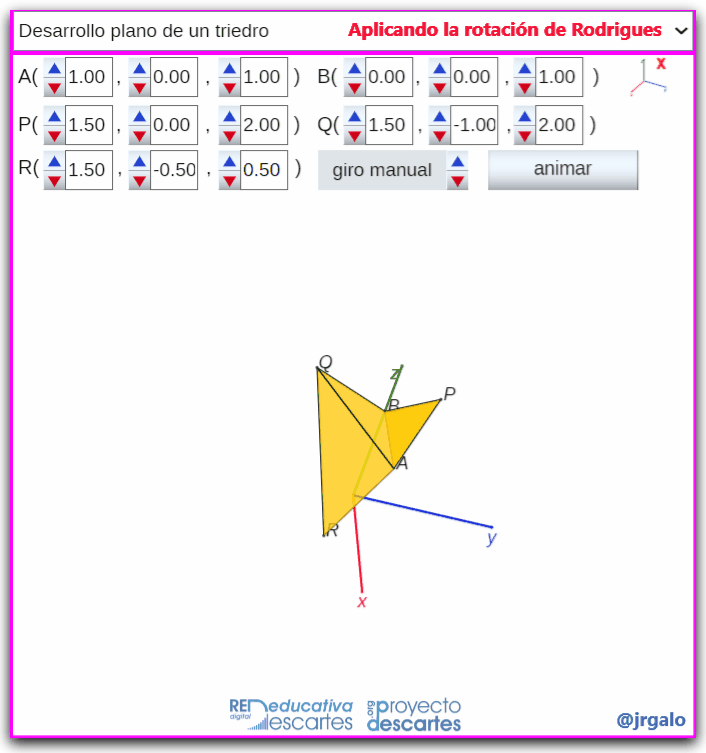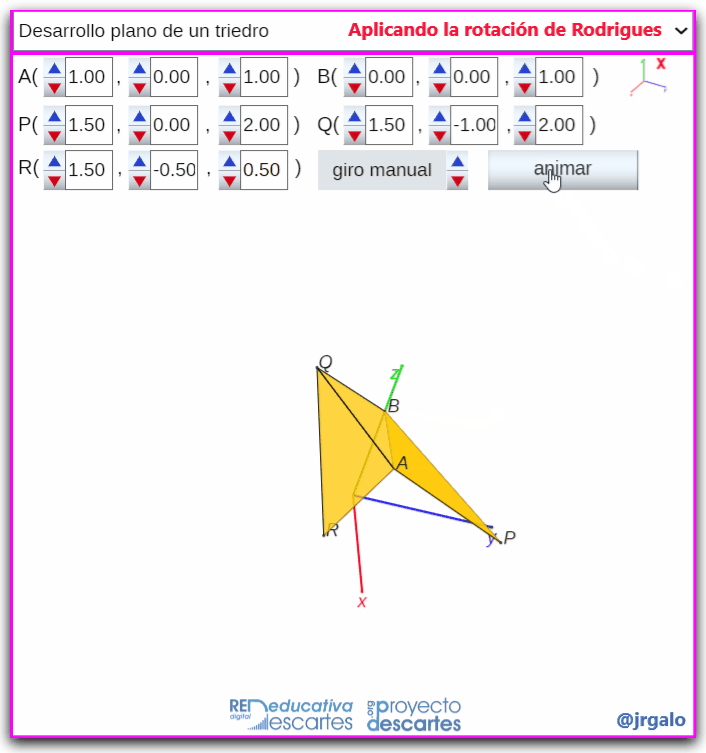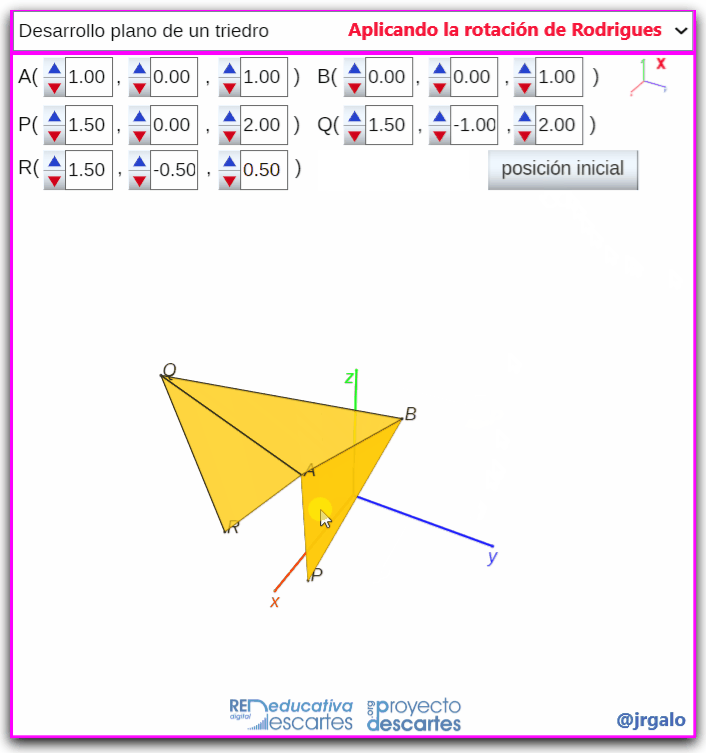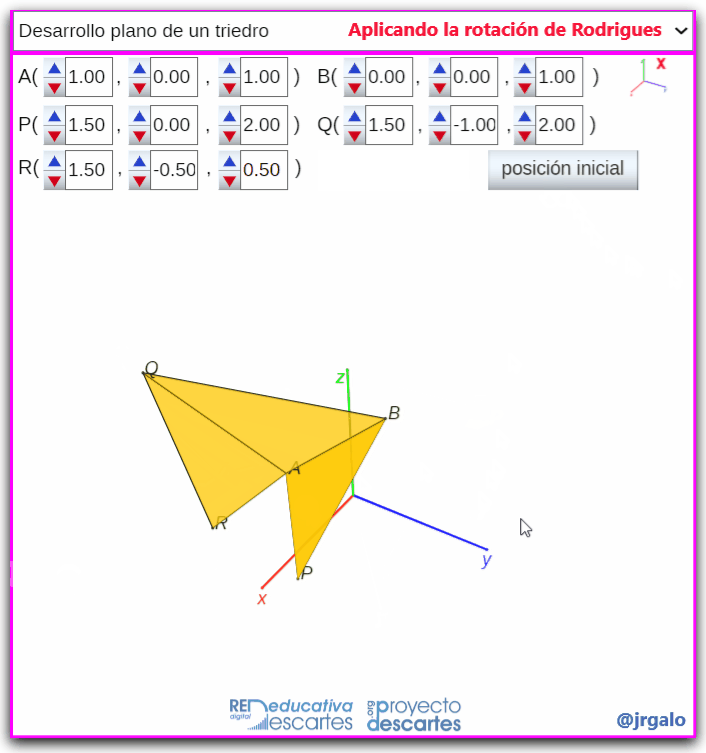
• Desarrollo plano de un triedro: Para obtener el desarrollo plano de un triedro, o de un ángulo poliedro en general, basta encadenar el desarrollo de pares de caras concurrentes.
  

  

  Pulsa sobre la imagen para ampliarla

• Desarrollo plano de un icosaedro: Como ejemplo final en esta escena se muestra la obtención automática de un desarrollo plano de un icosaedro regular.
  

  

  Pulsa sobre la imagen para ampliarla

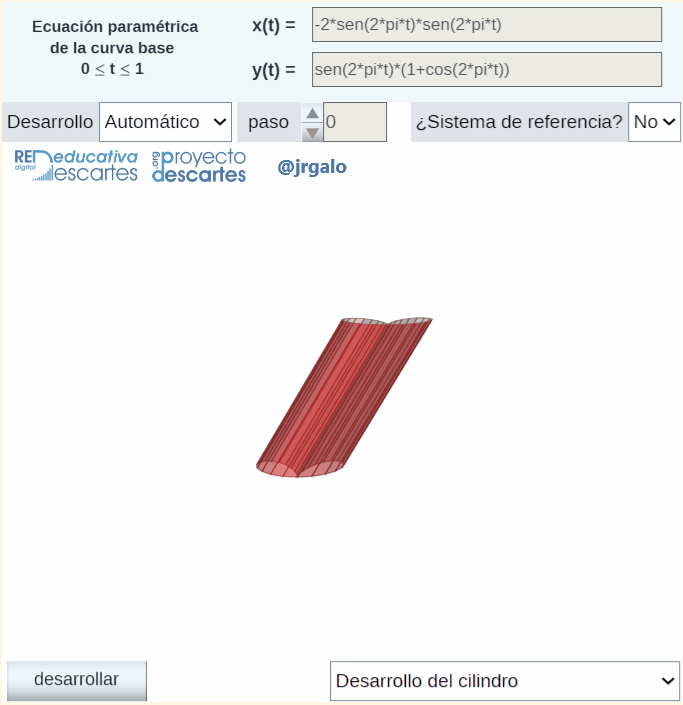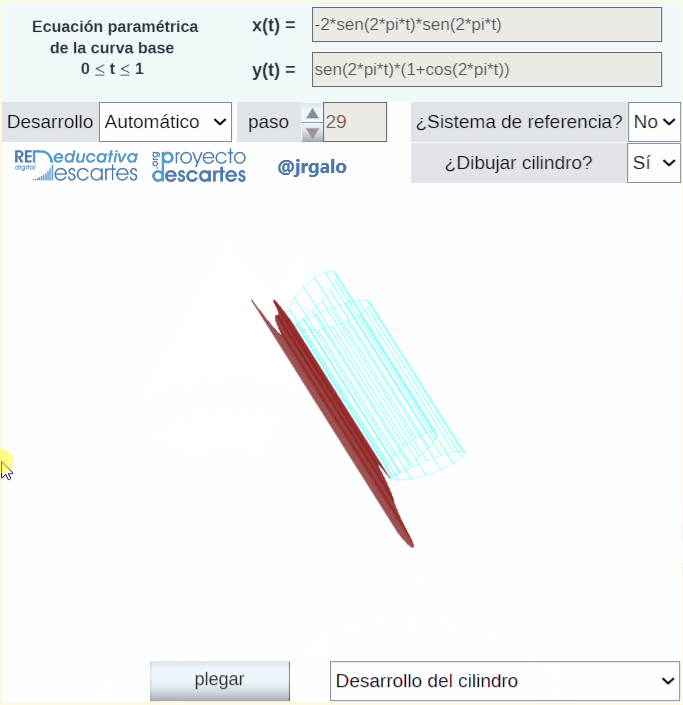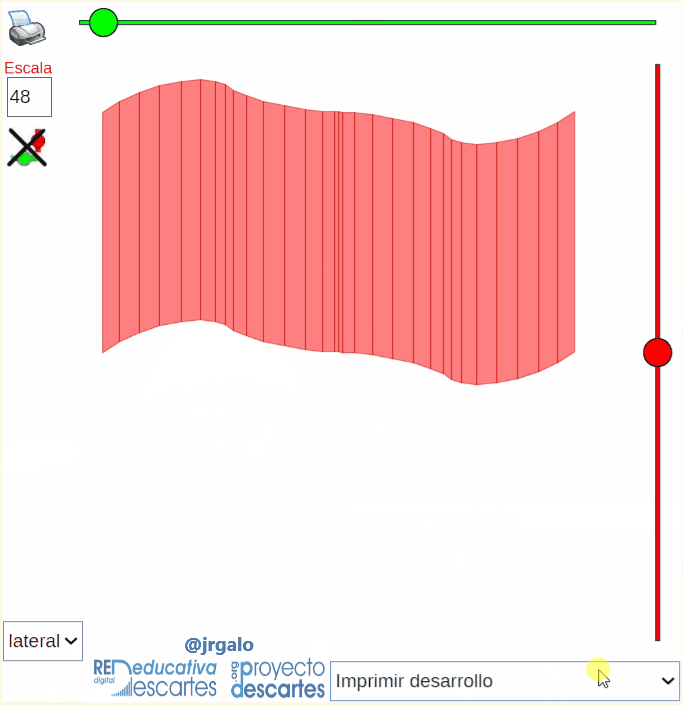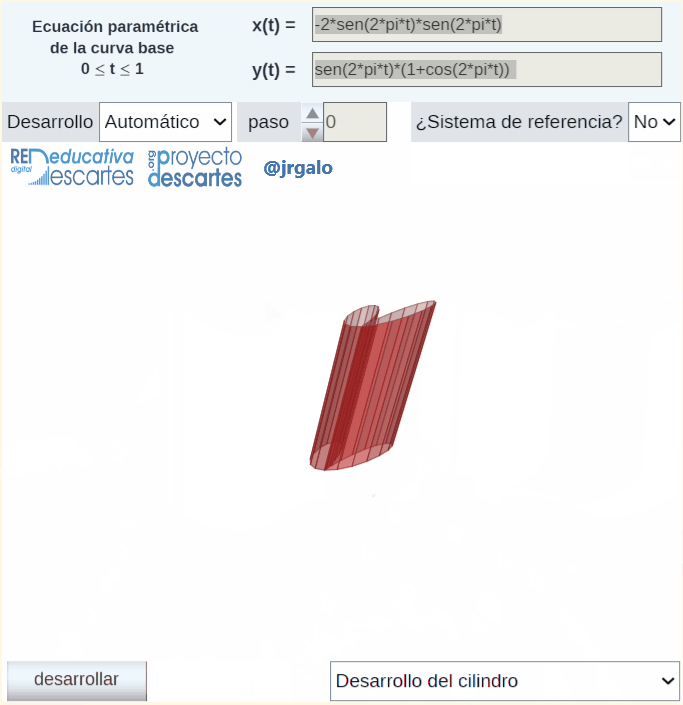
Otra muestra de aplicación de la rotación de Rodrigues es la obtención automática del desarrollo plano de un cilindro generalizado ya que éste puede plantearse como el desarrollo plano de un prisma que se ajuste suficientemente al cilindro dado. En la animación siguiente se plantea el desarrollo plano de un cilindro generalizado en el que su base es la curva denominada bifolium.  

Pulsa sobre la imagen para ampliarla

Este ejemplo y algunos más puede consultarse en la miscelánea "Ejemplos de cilindros generalizados" y también cada cual puede construir el cilindro generalizado que desee, obtener su respectivo desarrollo plano y construirlo físicamente con la miscelánea "Construyo mis cilindros".