A estas alturas de curso es bastante habitual trabajar algún tema de Geometría, por lo que me pareció oportuno compartir un SCORM de este bloque de contenidos. En concreto, realicé una adaptación de una escena en la que se practica la clasificación de cuadriláteros del tema "Polígonos, perímetros y áreas" de ed@d de 1ºESO.
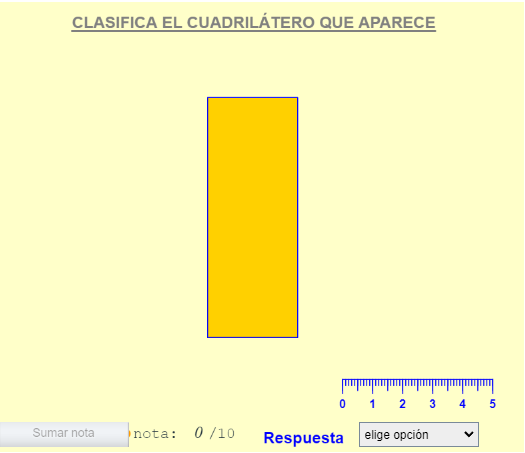
En la escena aparece un cuadrilátero junto con una regla para medir los lados si fuera necesario, y hay que decir si se trata de un cuadrado, un rectángulo, un rombo, un romboide o un trapecio. En la adaptación, añado un botón donde se suman los aciertos hasta realizar un total de 10 ejercicios, así como un texto que indica el número de aciertos logrados y, una vez completados los 10 ejercicios, aparece una pantalla resumen que indica el número de aciertos obtenidos y permite enviar la nota o reiniciar el ejercicio.
![]() Descargar ejercicio de clasificación
Descargar ejercicio de clasificación
Como siempre, se agradecen los comentarios o sugerencias.
Comienza la III Edición del curso para el Diseño de Libros Interactivos
Escrito por José Antonio Salgueiro GonzálezDurante la primera quincena del mes de marzo se ha desarrollado el proceso de inscripción en el curso para el "Diseño de libros interactivos", que forma parte del programa de Educación Abierta de RED Descartes, con tal grado de aceptación que, una vez más, ha superado nuestras expectativas. Una demanda de participantes procedentes de diecisiete países, 17, de habla hispana e inglesa, con docentes y profesionales de la educación que comprenden las etapas educativas de primaria, secundaria, bachillerato y universidad, así como una amplia gama de especialidades.
Compartimos el siguiente diagrama de sectores con el porcentaje de participación por países:
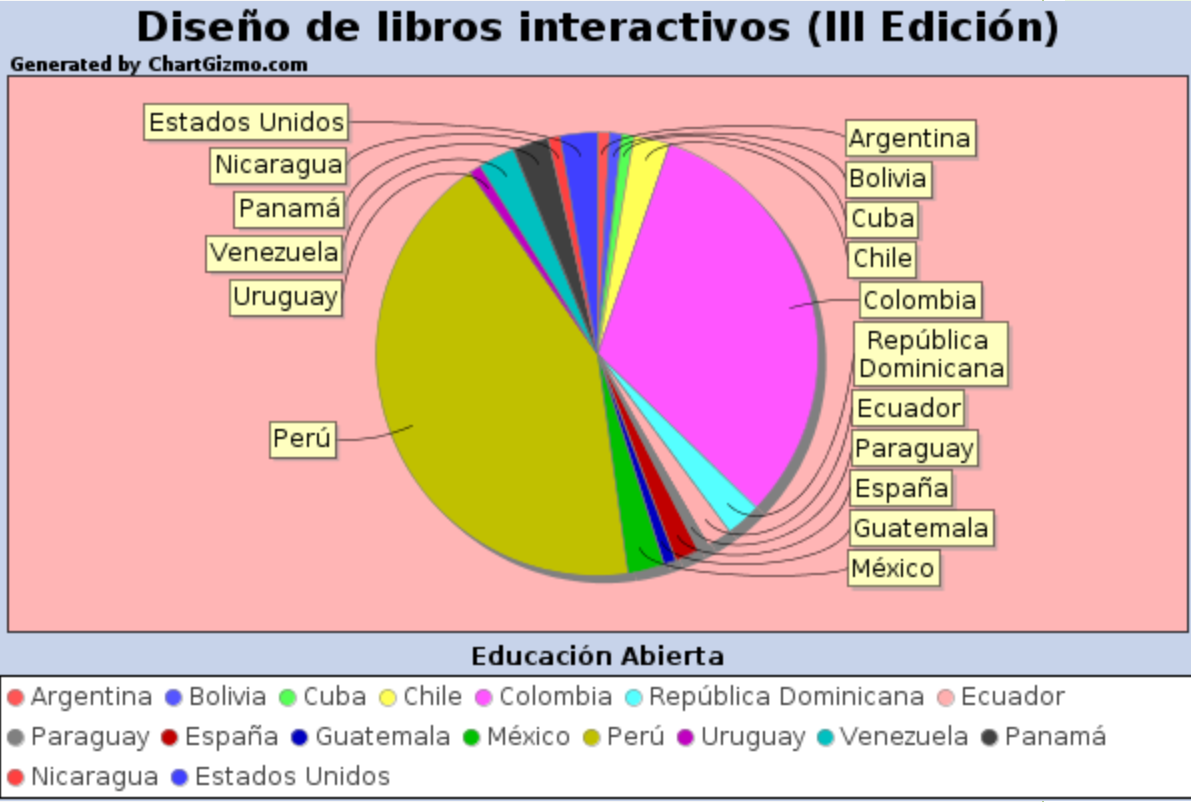
En esta ocasión, Perú se convierte en el país con mayor índice de participación, seguido muy de cerca por Colombia, que siempre ha liderado la formación en el diseño de libros interactivos, que se convierten en el soporte ideal para nuestras programaciones de aula, con facilidad para insertar o embeber la selección de recursos multimedia, la secuenciación de actividades o tareas para nuestro alumnado, los detalles del nuevo proyecto que pensamos desarrollar, las producciones digitales de nuestro alumnado y los proyectos de colaboración escolar, además de, obviamente, para su uso como libro del s. XXI.
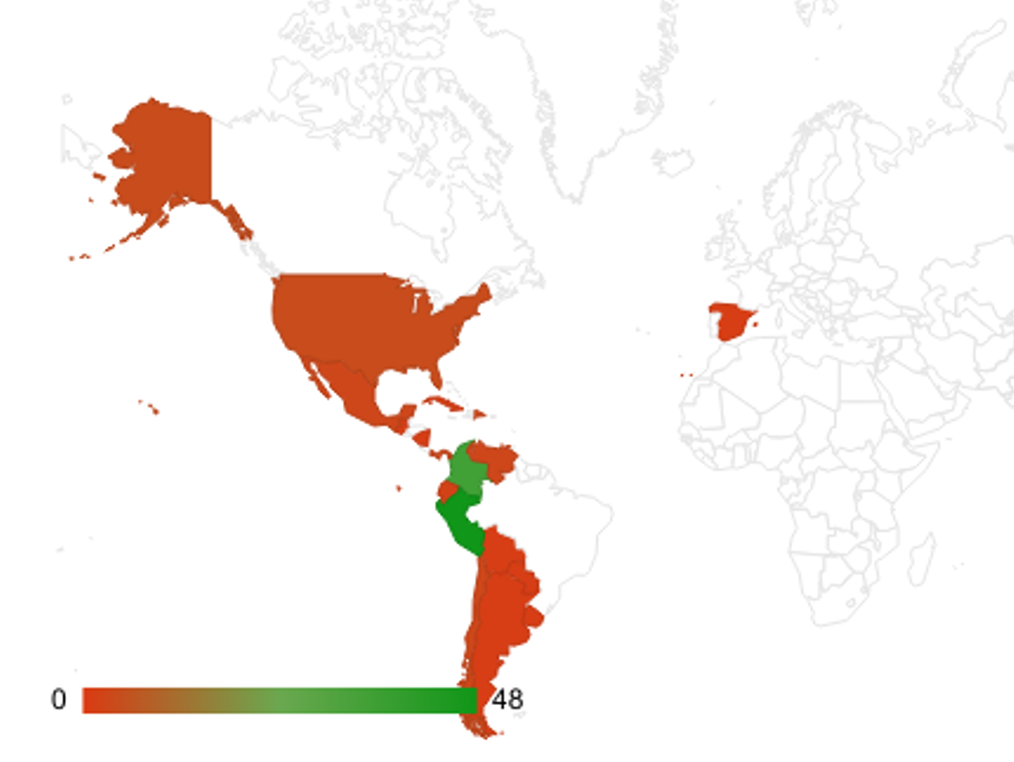
Con objeto de conocer visualmente el alcance geográfico del proyecto, compartimos una amplia zona del mapamundi, coloreando los países con participantes y de verde los mencionados con alto grado de implicación en esta nueva edición:
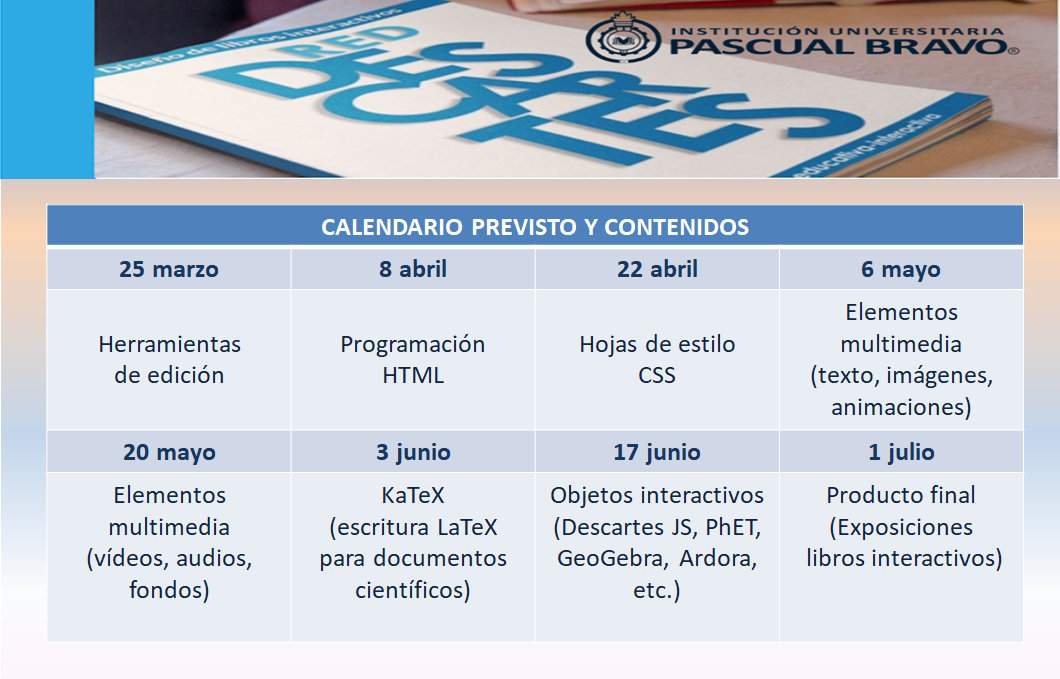
Recordamos a todos los participantes que el curso comienza el viernes 25 de marzo y finaliza el 1 de julio de 2022, impartiéndose las sesiones de 7 AM a 8 AM en el horario oficial de Colombia, de acuerdo al siguiente calendario previsto y contenidos a tratar:
Las sesiones se impartirán por videoconferencia usando la herramienta Meet de Google, para lo cuál, cada participante recibirá, tanto en su calendario de Google como en el grupo de Whatsapp del curso, el enlace de acceso a la reunión, que será grabada para, posteriormente, compartirla desde el grupo de Whatsapp y en el portal de la RED Descartes, donde se dispone, desde estos momentos, de algunas recomendaciones iniciales y de los enlaces para descargar las herramientas necesarias.
Desde la sesión inicial, independientemente del nivel de competencia digital, cada participante podrá comenzar a redactar y diseñar su primer libro interactivo, así que ¡ánimo a todos!, pues comenzamos una nueva y apasionante singladura.
Finalizamos compartiendo el vídeo de bienvenida, presentación e introducción al curso:
Difusión de ADJA y Descartes en la ETSI de la Universidad de Sevilla
Escrito por Jesús Manuel Muñoz Calle _
_Las matemáticas que unen. Día Internacional de las Matemáticas
Escrito por José Antonio Salgueiro GonzálezEn noviembre de 2019, la UNESCO proclamó el 14 de marzo de cada año como Día Internacional de las Matemáticas, con el fin de destacar el papel fundamental que desempeñan las ciencias matemáticas para hacer frente a los desafíos de nuestro tiempo en ámbitos como la inteligencia artificial, la salud, el cambio climático, la energía y el desarrollo sostenible y la mejora de la calidad de vida de la sociedad en general.
Para las personas que accedan por primera vez a esta información, debemos recordar que hemos venido celebrando desde hace años el conocido como "Día de π", una efemérides motivada por la forma de expresar la fecha diaria en el mundo anglosajón, es decir, 3/14, coincidiendo con las primeras cifras de este irracional número, considerado como una de las constantes matemáticas más importantes y conocidas.

En estos momentos, cuando vivimos y sufrimos lo peor de la raza humana, no podía haberse elegido mejor lema para la efemérides que "Las matemáticas que unen", que unen a las personas, que unen a los pueblos, que unen en el respeto, que unen en la diversidad, que unen en la admiración de cada cultura, que unen para vivir en paz en un lugar del Cosmos donde hay espacio para todos.
Como el fin de RED Descartes es promover la renovación y cambio metodológico en los procesos de aprendizaje y enseñanza de las Matemáticas, y también en otras áreas de conocimiento, utilizando los recursos digitales interactivos generados con la herramienta de autor Descartes JS, hemos recopilado una humilde colección de objetos interactivos con los que, cualquier docente que no haya podido planificar este evento previamente para su aula, o cualquier alumno o alumna autodidacta, puede participar desde un equipo tecnológico instalado en el aula o desde sus propios dispositivos móviles.
| APRENDE Y PRACTICA EL LENGUAJE UNIVERSAL QUE NOS UNE. EL LENGUAJE SIMBÓLICO DE LAS MATEMÁTICAS |
| LA ESTRATEGIA MATEMÁTICA QUE NOS UNE. ADIVINA UN NÚMERO ENTRE 1 Y 1000 |
| EL PASATIEMPO MATEMÁTICO QUE NOS UNE. AVERIGUA EL VALOR DE CADA OBJETO |
| EL CUADRADO MÁGICO QUE NOS UNE. FILAS, COLUMNAS Y DIAGONALES SUMAN LO MISMO |
| EL JUEGO MATEMÁTICO QUE NOS UNE. REGLA DE TRES SIMPLE DIRECTA PARA DOS EQUIPOS |
| EL PUZLE MATEMÁTICO QUE NOS UNE. PARA TODAS LAS EDADES |
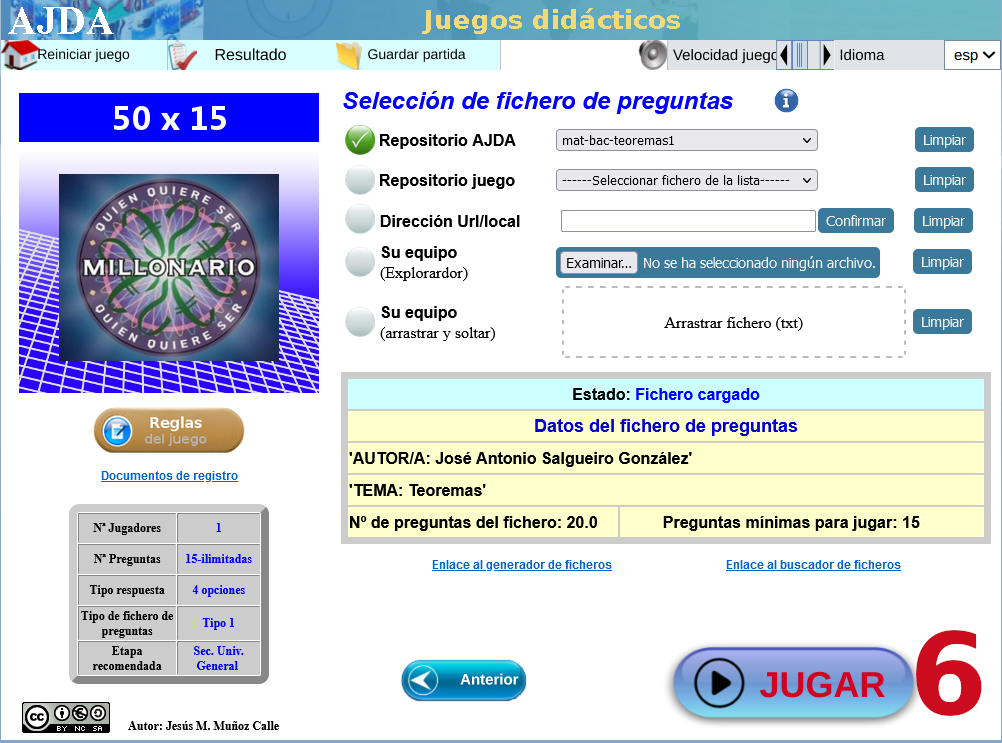
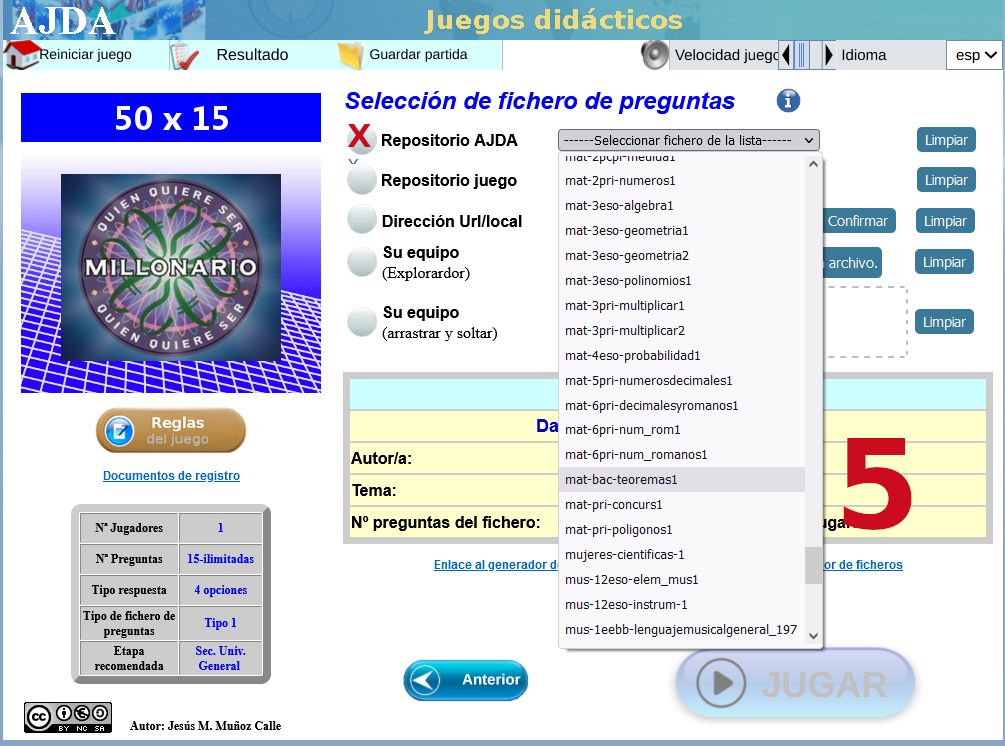
| LOS TEOREMAS QUE NOS UNEN |
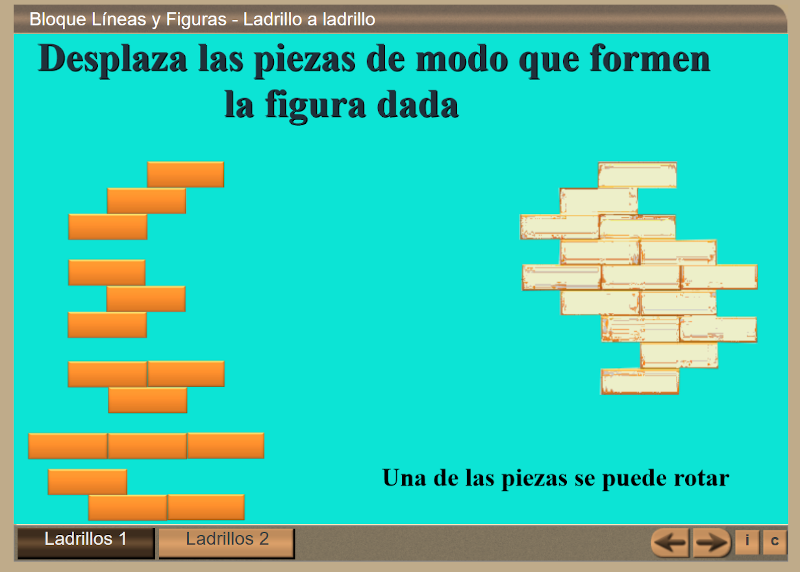
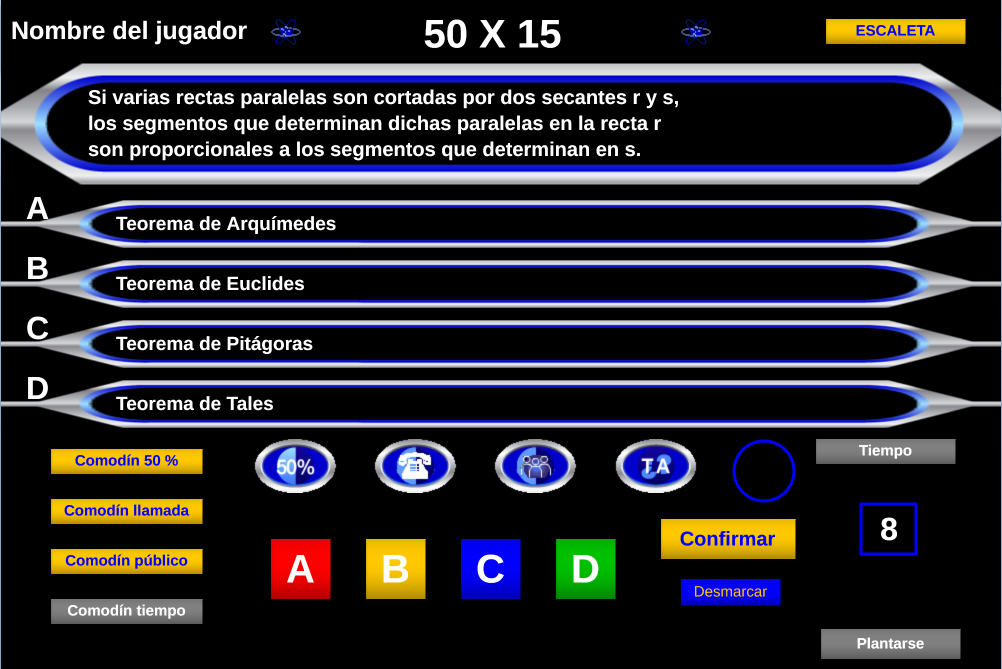
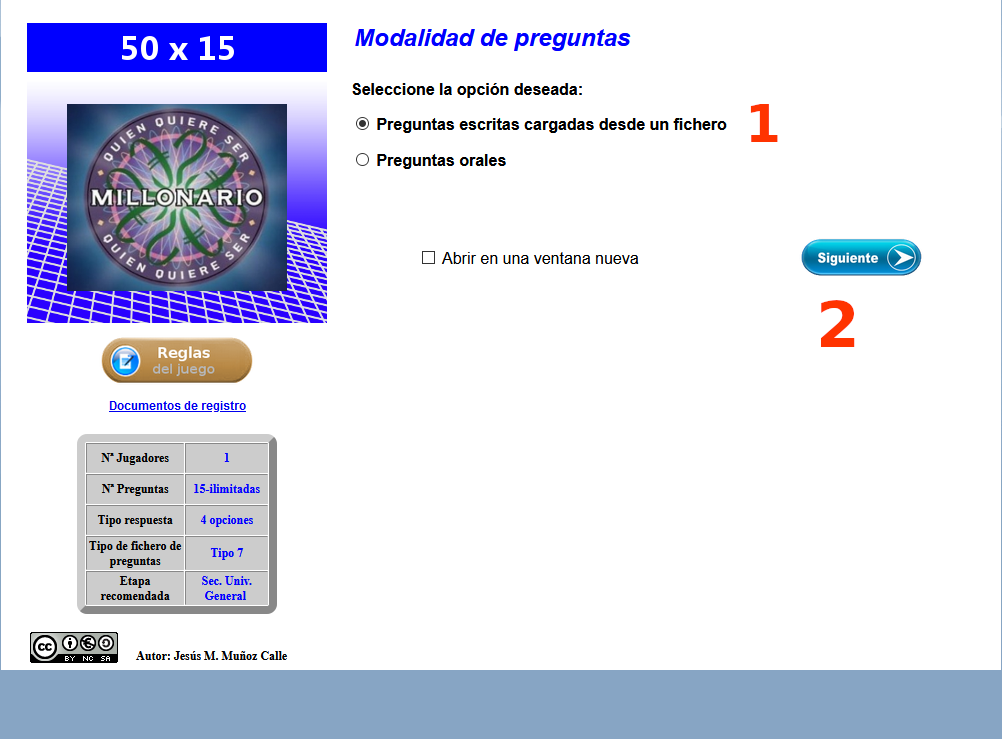
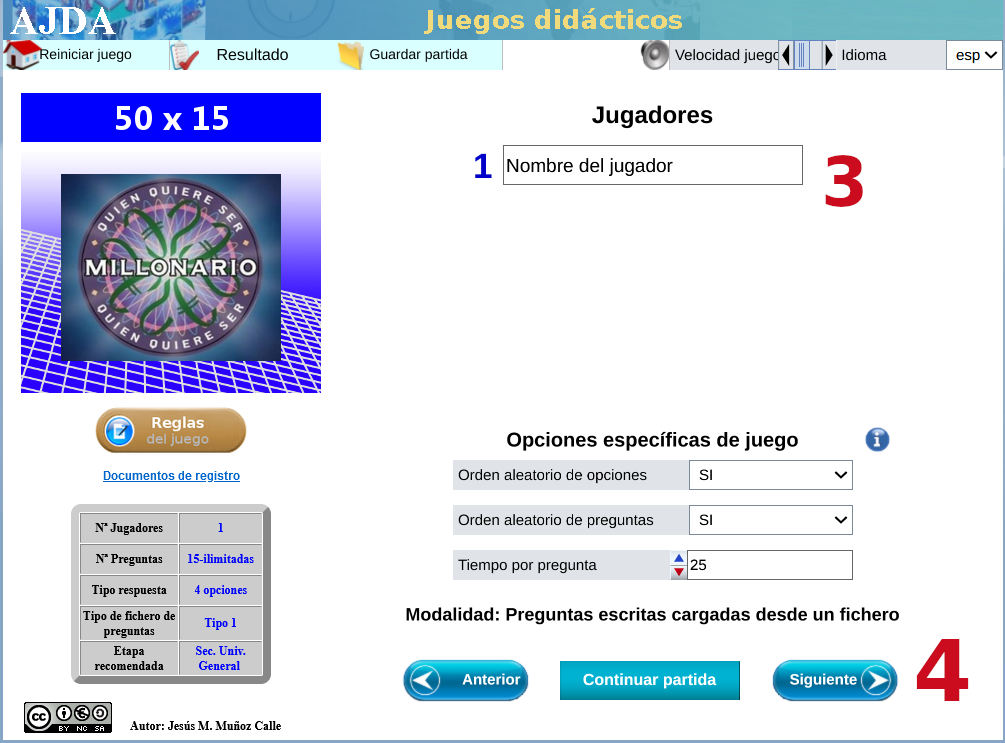
Juego didáctico basado en las matemáticas y sus teoremas, con una selección de veinte, la gran mayoría tratados y presentes en los diseños curriculares de esta materia en las etapas de educación secundaria obligatoria y bachillerato, aunque cada jugada dispone de quince preguntas con el formato del tradicional 50X15, ideal para presentarlo en la PDI del aula y organizar un par de equipos, con la posibilidad de buscar información, en caso de necesidad, en los dispositivos móviles del alumnado o el equipo tecnológico del espacio utilizado.
Con varias capturas de pantalla como tutorial, mostramos las sencillas instrucciones para acceder al juego didáctico, desde este enlace o sobre la imagen inferior.
Un año más, participamos en la Open Education Week
Escrito por José Antonio Salgueiro GonzálezLa Semana de la Educación Abierta (Open Education Week) es una oportunidad para compartir activamente y aprender sobre los últimos logros en Educación Abierta en todo el mundo. OE Week brinda a los profesionales, educadores y estudiantes la oportunidad de obtener una mayor comprensión de las prácticas educativas abiertas y de inspirarse en el maravilloso trabajo que está desarrollando la comunidad en todo el mundo. Unos objetivos que encajan perfectamente con el lema de Red Descartes: "trabajando altruistamente por la comunidad educativa de la aldea global". Por ello, en esta nueva edición, que se desarrolla durante los días comprendidos entre el 7 y el 11 de marzo de 2022, desde Proyecto Descartes hemos decidido colaborar, compartir y aportar algunos de nuestros proyectos en la línea de la OE Week, centrándonos en los más recientes y abarcando las diferentes líneas de la Educación Abierta.
Pero antes, para nuestros seguidores, docentes, comunidad educativa y ciudadanía, en general, conviene recordar el origen oficial y concepto de Recurso Educativo Abierto, que aparece en París en junio de 2012, durante el Congreso Mundial sobre los Recursos Educativos Abiertos (REA), y que "designa a materiales de enseñanza, aprendizaje e investigación en cualquier soporte, digital o de otro tipo, que sean de dominio público o que hayan sido publicados con una licencia abierta que permita el acceso gratuito a esos materiales, así como su uso, adaptación y redistribución por otros sin ninguna restricción o con restricciones limitadas". Una definición cuyos requisitos cumplen escrupulosamente los recursos interactivos generados con la herramienta de autor Descartes JS y compartidos con la aldea global en el portal de la ong RED Descartes.

| RECURSOS EDUCATIVOS ABIERTOS EN LENGUA PORTUGUESA | ||
 |
 |
 |
 |
 |
 |
 |
 |
 |
| FORMACIÓN ABIERTA | |
 |
 |
Además de los recursos educativos abiertos en lengua portuguesa y de los cursos para formación, a los que puede accederse desde cada imagen al espacio de la Open Education Week, desde RED Descartes hemos presentado nuestra revista digital y la herramienta de autor de software libre Descartes JS, el pilar sobre el que se sostiene nuestra RED.
| REVISTA DIGITAL RED DESCARTES |
 |
¿Por qué es importante la Educación Abierta?
La gente quiere aprender. Al proporcionar acceso gratuito y abierto a la educación y al conocimiento, la educación abierta ayuda a crear un mundo para apoyar el aprendizaje. Los estudiantes pueden obtener información adicional, puntos de vista y materiales para ayudarlos a tener éxito. Los trabajadores pueden aprender cosas que los ayudarán en el trabajo. La facultad puede recurrir a recursos de todo el mundo. Los investigadores pueden compartir datos y desarrollar nuevas redes. Los maestros pueden encontrar nuevas formas de ayudar a los estudiantes a aprender.
Las personas pueden conectarse con otras personas que de otra manera no se encontrarían para compartir ideas e información. Los materiales se pueden traducir, mezclar, dividir y compartir abiertamente de nuevo, lo que aumenta el acceso e invita a nuevos enfoques. Cualquiera puede acceder a materiales educativos, artículos académicos y comunidades de aprendizaje de apoyo en cualquier momento que lo deseen. La educación está disponible, accesible, modificable y gratuita".
(El párrafo anterior ha sido extraído literalmente de la web de la Open Education Week)
| HERRAMIENTA DE AUTOR DE SOFTWARE LIBRE DESCARTES JS |
 |
En nuestro modelo uniforme del Nautilus (Galo et al. 2016) detectamos que los septos son arcos de espirales cordobesas y, adicionalmente, que sus respectivos polos estaban ubicados también en una espiral cordobesa. Ése fue, quizás, el mayor y más novedoso avance logrado en la modelación de esta concha. No obstante, allí, no abordamos la evidente diferencia que acontece entre ellos según las etapas vitales de estos especímenes y, consecuentemente, lo que ocurre también en las cámaras septales que determinan. En especial, esas diferencias se presentan entre el primer verticilo y en los dos restantes. Allí, tampoco profundizamos en el modelado de las intersecciones de los septos con la pared ventral y la dorsal y sólo aventuramos una posible base teórica del fragmacono en base al gnomon de un triángulo cordobés. Ahora, habiendo profundizado en el estudio de la literatura existente sobre la ontogenia biológica del Nautilus y también en el análisis matemático del modelo propuesto entonces, es el momento de adentrarnos en un modelo matemático diferenciado por fases, es decir, de abordar la ontogenia matemática de los septos.
Siguiendo lo indicado en los artículos anteriores de esta serie (puede consultar: I, II, III y IV), y en particular en lo relativo a la modelación de la pared dorsal y ventral de la sección sagital de la concha, partimos de una base o fundamento primordial que es el que justifica y explica el distinto comportamiento de los septos entre el primer verticilo y los siguientes. En el primero, ambas paredes se corresponden con arcos de dos espirales cordobesas que tienen diferente polo, sin embargo, en el segundo y en el tercer verticilo las espirales de ambas paredes son copolares, tienen el mismo polo, siendo realmente arcos de una única espiral con un retardo angular entre ambas de 2π. Así pues, dado que la complejidad es mayor en el primer verticilo vamos a proceder en orden cronológico inverso y analizaremos en primer lugar el segundo y tercer verticilo y posteriormente el primero.
Los septos en el segundo y tercer verticilo
La pared ventral en el segundo y tercer verticilo viene dada por
 (20)
(20)
donde θi es el ángulo que marca el inicio de la concha embrionaria y θf la terminación de la misma delimitando la boca de la concha.
Y en el mismo instante[1] angular vital θ, la pared dorsal sería:
 (21)
(21)
La espiral que contiene a los polos de los septos es:
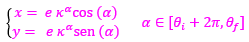 (22)
(22)
donde e es un factor de escala o de retardo en la espiral cordobesa [2].
Y cada septo, ver (11 en IV), es un arco de una espiral:
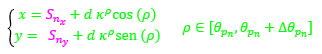 (23)
(23)
donde 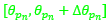 determina la amplitud angular del arco de esa espiral que comprende el septo n-ésimo; ρ determina unívocamente cada uno de los puntos de dicho septo, pero todos ellos se corresponden con un mismo instante vital[3]; d es un factor de escala o de retardo a determinar en el modelo; y
determina la amplitud angular del arco de esa espiral que comprende el septo n-ésimo; ρ determina unívocamente cada uno de los puntos de dicho septo, pero todos ellos se corresponden con un mismo instante vital[3]; d es un factor de escala o de retardo a determinar en el modelo; y 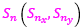 es el polo de la espiral que incluye a ese arco septal n-ésimo y que perteneciendo a la espiral (22) quedará determinado por un valor αn.
es el polo de la espiral que incluye a ese arco septal n-ésimo y que perteneciendo a la espiral (22) quedará determinado por un valor αn.
La aplicación en el modelo de la que hemos denominado invariante tercera (tangencialidad entre la pared ventral y las paredes de los septos) nos puede llevar a determinar los parámetros antes citados. De partida:
- Toda espiral logarítmica es equiangular, así pues, en cualquier punto de la espiral la recta tangente y el radio vector forman siempre un mismo ángulo ψ. Éste es característico de cada tipo espiral y depende sólo de la base b que la define, siendo
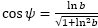 . En el caso de una espiral cordobesa este ángulo es ψ ≃ 80,32º, al ser la base logarítmica o exponencial que la define κ = 1,185580...
. En el caso de una espiral cordobesa este ángulo es ψ ≃ 80,32º, al ser la base logarítmica o exponencial que la define κ = 1,185580... - Al ser tangentes la espiral ventral y la septal, ambas comparten la misma recta tangente. Y dado que ambas espirales son cordobesas entonces, consecuentemente, los radios vectores de ambas han de estar también en la misma recta, porque ambos han de formar el mismo ángulo con la tangente común.
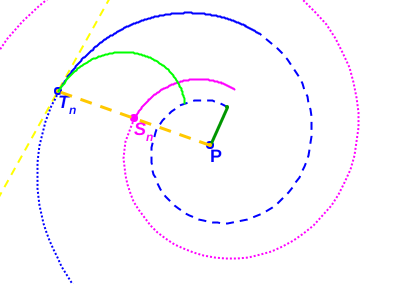
(i) Espiral azul discontinua: pared dorsal en el segundo verticilo. (ii) Espiral azul continua y de puntos: pared ventral en el segundo verticilo.
(iii) Espiral magenta: espiral de los polos de los septos. (iv) Tn: punto de tangencia septo y pared ventral; Sn: polo del septo y P: polo común de la espiral dorsal, de la ventral y de la de los polos de los septos.
Fig. 40. Tangencialidad de los septos con la pared ventral.
Por tanto (ver Fig. 40), si Tn es el punto de tangencia del n-ésimo septo (con n>8, pues en el primer verticilo hay ocho septos), Sn es el polo de éste y P el polo de la pared ventral, tenemos que:
- Al ser Tn un punto de la espiral ventral, entonces:
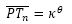 (24)
(24)
para algún θ.
- Al ser Sn un punto de la espiral de los polos de los septos, por (22),
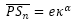 (25)
(25)
donde α = θ al estar alineados P, Sn, y Tn y ser P el polo común a la espiral ventral (20) y a la espiral de los polos de los septos (22).
- Al ser Tn un punto del septo n-ésimo
![]() (26)
(26)
para algún valor de d y ρ.
Y dado que
![]() (27)
(27)
de las relaciones anteriores, (24) a (26), obtenemos que:
![]() . (28)
. (28)
Expresando en (28) d = d' κθ - ρ, es decir, considerando que ρ es un ángulo de retardo, tenemos:
![]() (29)
(29)
Y de ahí
d' = 1 - e. (30)
En Galo et al. (2016) detectamos que en la espiral de los polos de los septos (22) e ≃ 0,5 e igual acontecía para la espiral que da forma a los arcos de los septos. Aquí la relación obtenida en (30) conduce a considerar que e = 0,5 (exactamente ese valor[4]), pues en ese caso también es d' = 0.5, y consecuentemente la espiral correspondiente a un determinado arco septal se obtiene sin más que realizar una traslación de la espiral de los polos para que el polo de ésta coincida con el polo de dicho septo. (ver fig. 41).
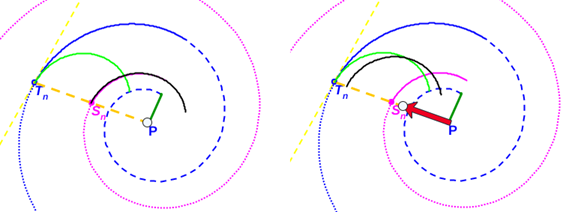
Fig. 41. Obtención de un arco septal como traslación de un arco de la espiral de los polos.
Intersección de la pared dorsal y los septos en el segundo y tercer verticilo
Centrémonos ahora en la determinación de la intersección de los arcos de los septos con la pared dorsal y la amplitud de estos.
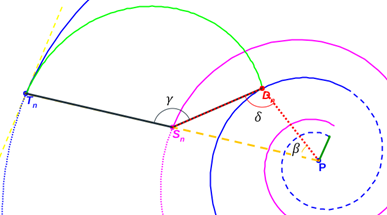
Fig. 42. Parámetros que definen los septos en el segundo y tercer verticilo.
Para el septo n-ésimo, según la denominación de los ángulos reflejados en la fig. 42 y fijado el valor de e = 0,5, por (25) tenemos que:
![]() (31)
(31)
El punto Dn, intersección de ese septo con la pared dorsal, por pertenecer a ella y según (21) verifica que
![]() (32)
(32)
y, a su vez, por pertenecer al arco del septo:
![]() (33)
(33)
- Aplicando el teorema del coseno en el triángulo de vértices P, Sn y Dn:
![]() (34)
(34)
y considerando las expresiones (31), (32) y (33) llegamos a la igualdad:
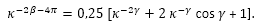 (35)
(35)
- Aplicando el teorema del coseno en el triángulo de vértices Tn, Sn y Dn, y teniendo en consideración que
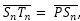 obtenemos que:
obtenemos que:
![]() (36)
(36)
Y puesto que las coordenadas de los puntos que intervienen en esa igualdad son:
![]()
se tiene que:
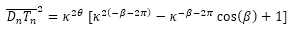 (37)
(37)
Y teniendo en consideración (31) y (33)
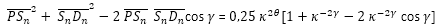 (38)
(38)
Por tanto, la igualdad (36) queda expresada como:
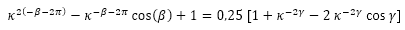 (39)
(39)
A partir de (35) y (39) tenemos un sistema de dos ecuaciones que nos relaciona al ángulo γ (amplitud del arco del septo), con el β (retardo del punto de intersección dorsal del septo Dn, respecto al punto de intersección ventral Tn). Este sistema puede reescribirse como:
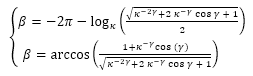 (40)
(40)
Es decir,
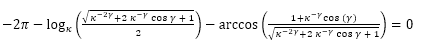 (41)
(41)
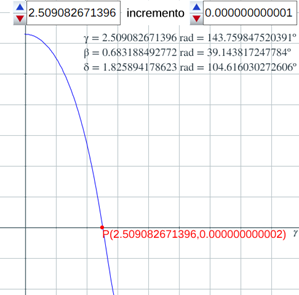
Escena interactiva 5. Determinación numérica de la amplitud del septo.
Pulse sobre la imagen para interactuar libremente con ella.
La resolución numérica de la ecuación (41) (puede observarse en la escena interactiva 5, donde la gráfica en azul se corresponde con la función en la variable γ, definida por la expresión del miembro de la izquierda en (41) con 0 ≤ γ ≤π) nos permite determinar:
- La amplitud del septo
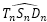 : γ = 2,5090... radianes ≃ 143,76º.
: γ = 2,5090... radianes ≃ 143,76º. - El desplazamiento entre la intersección dorsal y la ventral
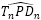 : β = 0,6831... radianes ≃ 39,14º.
: β = 0,6831... radianes ≃ 39,14º. - El ángulo entre los radios vectores
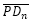 y
y 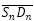 :
: 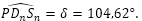
Apoyándonos en que en una espiral cordobesa el ángulo que forma el radio vector con la recta tangente es de 80,32 º tenemos que (ver Fig. 43) el ángulo que forma la recta tangente a la pared dorsal en Dn con la recta tangente al septo en ese mismo punto es de 75,38º, es decir el septo no interseca a la pared dorsal perpendicularmente, si no formando con respecto a esa perpendicular un ángulo de 14,62º. Eso concuerda con lo indicado por Mutvei & Doguzhaeva (1997), que ya reflejamos en la figura 20, y la depresión septal dorsal en el área media ―sección o corte que es el que estamos analizando en este estudio― lo que hace es corregir dicha desviación respecto a la perpendicular buscando aportar y lograr, quizás, una mayor consistencia (eso es lo que puede interpretarse de este hecho aportado por la matemática).
Este comportamiento teórico es el mismo tanto en el segundo como en el tercer verticilo, pues en ambos casos la pared dorsal y ventral comparten el mismo polo. En el tercer verticilo, esa depresión dorsal parece ser menos notable, al menos aparentemente, si bien sí pueden visualizarse o intuirse (interactuar por ejemplo con la digitalización del Nautilus del Museo Dundee ―figura 22―). Matemáticamente no hay diferencia.
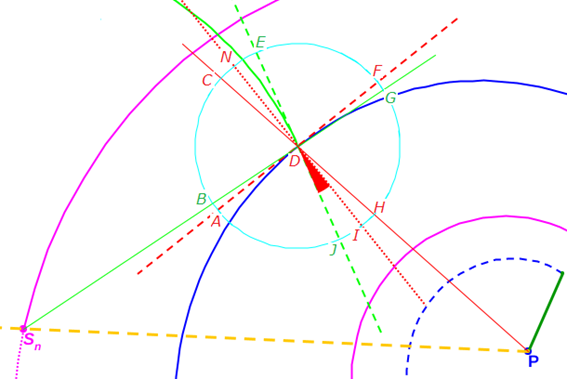

Fig. 43. Ángulo de incidencia entre septo y pared dorsal en el segundo y tercer verticilo.
Ecuaciones del modelo
Así pues, en estos dos verticilos los arcos de los septos tienen por ecuación (23), donde para cada n ≥ 8 (en el primer verticilo hay ocho septos y el octavo da inicio al segundo) tenemos que:
- d = 0,5.
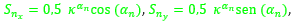 siendo
siendo 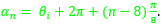
- ρ ∈ [ αn - γ, αn ], con γ = 2,5090...
Los puntos de tangencia son: Tn ( ![]() ) y los de intersección con la pared dorsal pueden escribirse:
) y los de intersección con la pared dorsal pueden escribirse:
- como punto de la pared dorsal: Dn (
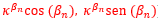 ), donde denotamos βn = αn - 2π - β con β = 0,6831.
), donde denotamos βn = αn - 2π - β con β = 0,6831. - como punto del arco de septo:
 ,
, 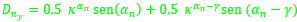 .
.
Síntesis
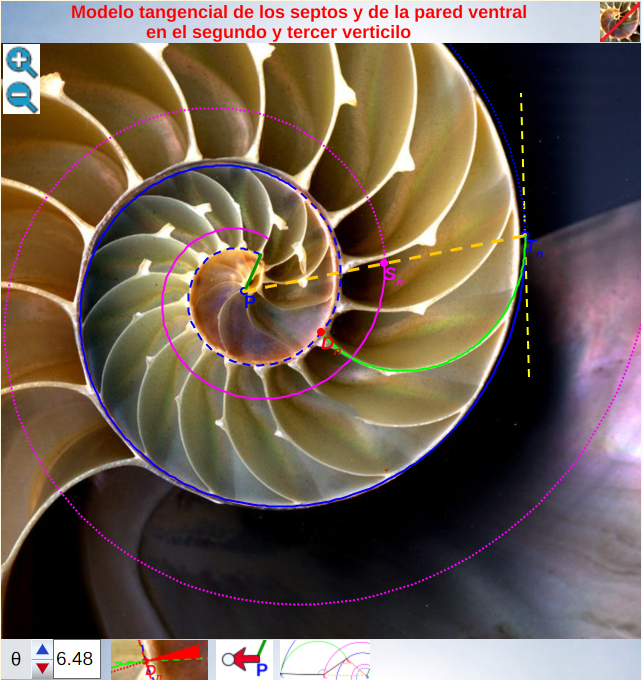
La introducción de la tangencialidad entre la pared ventral y los septos nos ha permitido lograr la modelación matemática de la sección sagital del Nautilus en el segundo y tercer verticilo y acentuar el caracter cordobés de sus elementos. En la escena interactiva 6, podemos observar e interactuar con este modelo.
Escena interactiva 6. Modelo tangencial de los septos y de la pared ventral en el segundo y tercer verticilo.
Pulse sobre la imagen para interactuar libremente con ella.
El camino seguido en el análisis anterior nos puede servir de guía para abordar el estudio de los septos en ese primer verticilo tan especial. Especial por ser la pared dorsal y la ventral espirales cordobesas con distinto polo y, como veremos, por ser ésta la causa esencial de esas cámaras diferentes y esos septos variables. Un estudio que considero es interesante y matemáticamente bonito. Pero siento dejarles con la miel en los labios ya que lo dejaré para un nuevo artículo... espero no tenerles en vilo mucho tiempo.
Bibliografía
Galo J.R., Cabezudo A. y Fernández I.(2016) : Sobre la forma y crecimiento cordobés del Nautilus Pompilius. Epsilon, 2016, Vol. 33 (3), nº 94.
Mutvei, H. and Doguzhaeva, L. (1997): Shell ultrastructure and ontogenetic growth in Nautilus pompilius L. (Mollusca: Cephalopoda). Palaeontographica Abteilung A Palaeozoologie–Stratigraphie, vol. 246, p. 33–52.
Ward, P. (1979). Cameral liquid in Nautilus and ammonites. Paleobiology, 5(1), pp. 40-49.
Ward, P., Greenwald, L., & Magnier, Y. (1981). The chamber formation cycle in Nautilus macromphalus. Paleobiology, 7(4), 481-493. doi:10.1017/S0094837300025537
[1] Al no tener una referencia temporal del crecimiento del Nautilus, sólo podemos señalar un mismo instante vital teórico mediante el uso de una amplitud angular común. De esta manera establecemos momentos, atemporales, en la que se han de dar coincidencias vitales. En este caso, para un valor fijado de θ, conocemos el punto de la pared ventral y el punto de la pared dorsal que están relacionados entre sí.
[2] En estos verticilos, en el modelo uniforme se detectó que e ≃ 0,5, que es un valor próximo al valor medio del factor correspondiente al sifúnculo y al del de la pared dorsal ―Galo et al., 2016―.
[3] Para conocer el proceso de formación de las cámaras de los nautilos podemos acudir a lo estudiado y analizado por Ward, Greenwald y Magnier (1981) en su artículo “The chamber formation cycle in Nautilus macromphalus”. Estos autores basan su estudio en la observación radiográfica (ver figura 26) de diferentes ejemplares en distintos momentos y, así, pueden analizar las variaciones que acontecen y realizar mediciones que llevan a plantear un crecimiento periódico que comprende tres fases:
- Formación de una cresta mural en la posición que ocupará el nuevo septo. Esta cresta es una delgada banda anular interna de carbonato cálcico.
- Desplazamiento hacia delante del manto septal para ubicarse a la altura de la cresta mural y ajustarse a ella. Inicio del proceso de calcificación del nuevo septo. También el sifúnculo comienza a calcificar un anillo de conexión en el interior de la nueva cámara uniendo el septo anterior y el nuevo. Durante esta fase la nueva cámara está llena de líquido cameral (Ward, 1979) y no acontece ningún vaciado de la misma, pero ese vaciado sí continúa en las cámaras anteriores.
- Vaciado del líquido de la nueva cámara, que se inicia cuando el nuevo tabique ha alcanzado de un tercio a dos tercios de su espesor final. Este vaciado se denomina acoplado pues el líquido está en contacto con el anillo de conexión sifuncular. En esta fase el tabique septal sigue construyéndose, engrosándose, finalizando este proceso cuando el volumen del líquido vaciado es aproximadamente el 50% y ya no está en contacto con el anillo sifuncular, momento en el que se pasa a un proceso de vaciado desacoplado y comienza la formación de una nueva cresta mural y, consecuentemente, un nuevo ciclo.
Durante el ciclo de formación de una cámara, el crecimiento de la concha exterior parece ser que es continuo, pero hay una correlación inversa entre el porcentaje de líquido que se ha vaciado en la última cámara construida y la amplitud angular de la cámara habitacional. A medida que la cámara septal está más vacía la cámara habitacional es mayor y viceversa. Esta relación logra mantener la flotabilidad ya que cuando la nueva cámara está más llena de líquido el peso de la concha en la zona habitacional es menor y a medida que decrementa el líquido aumenta la amplitud de la zona habitacional. El inicio de cada cámara representa un punto crítico para la flotabilidad global, pero esto se compensa con el vaciado desacoplado que sigue aconteciendo en las cámaras anteriores.
[4] También se apuntó la posibilidad de que ese valor correspondiera a la espiral intermedia entre la del sifúnculo y la pared dorsal, es decir, ![]() , pero en este caso d' ≠ e, es decir las dos espirales citadas son diferentes. De ahí que optemos por el valor e = 0.5.
, pero en este caso d' ≠ e, es decir las dos espirales citadas son diferentes. De ahí que optemos por el valor e = 0.5.

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Abierto el plazo de inscripción en la III Edición del Curso para el Diseño de Libros Interactivos
Escrito por José Antonio Salgueiro GonzálezSe encuentra abierto el plazo de inscripción en la III Edición del curso para el diseño de libros interactivos, acción que se enmarca en el programa de Educación Abierta desarrollado entre redes docentes de Colombia, México y España, fundamentalmente, aunque contamos con la participación de profesorado de otros países de habla hispana y portuguesa. Este curso tiene como objetivo principal abordar la conceptualización y el diseño, desarrollo y experimentación de nuevos recursos educativos abiertos en formato libro del s. XXI y basados en la interactividad, que permitan poner de manifiesto que es posible dar una respuesta positiva y asequible a los retos educativos intrínsecos al paradigma educativo emergente.
Está dirigido a docentes de cualquier etapa educativa, infantil, primaria, educación secundaria obligatoria, bachillerato, formación profesional, enseñanzas de régimen especial y universidad, y de cualquier materia o especialidad, en activo o no, así como a profesionales vinculados a la educación o formación, utilizando una metodología activa, pues desde la primera sesión cada participante comenzará a diseñar y editar su proyecto de libro interactivo, recibiendo sesiones quincenales por videoconferencia, que serán grabadas y compartidas con todos los participantes y asesorados por docentes de las redes mencionadas.
El curso comienza el día 25 de marzo y finaliza el 1 de julio de 2022, impartiéndose las sesiones de 7 AM a 8 AM en el horario oficial de Colombia, de acuerdo al siguiente calendario previsto y contenidos a tratar:

Según las necesidades y proyectos de cada participante, el producto final podrá ser como los mostrados a continuación:
- Libro digital interactivo: artes visuales, ciencias computacionales, ciencias administrativas y económicas, ciencias sociales y humanas, formación, matemáticas, física, química, ingeniería, lengua inglesa, literatura...
- Revista digital interactiva
- Revista digital RED Descartes - 1
- Revista digital RED Descartes - 2
También puedes ampliar información en el artículo titulado "El libro interactivo al alcance de cualquier docente, etapa educativa y materia".
| PLAZAS AGOTADAS. INSCRIPCIÓN CERRADA |
Recursos que utilizaremos:
- Descarga tu plantilla inicial
- Ejemplo básico de uso
- Descarga del libro de ejemplo básico de uso
- Ejemplo de libro interactivo con fórmulas con KaTeX, específico para el lenguaje científico
- Descarga del libro con fórmulas con KaTeX
- Tutorial para el diseño de libros interactivos
- Lista en Youtube con vídeos de apoyo
- Curso "Edición de libros interactivos" de la RED Descartes
Tras la magnífica acogida que la "Escuela de Alquimia" ha tenido entre el alumnado, hemos realizado ampliaciones en la "academia", de forma que se mantenga todo lo que hay y los objetivos del juego, pero aumentando el número de estancias y las opciones disponibles. Además introduce como parte de la mecánica del juego la realización de cuestionarios de preguntas. Comentamos a continuación las principales novedades.
En la sala de recaudación se pueden conseguir "tiradas mágicas" a través de cuestionarios de preguntas, además de la forma establecida en Alquimistas 1.
Desde la sala de alquimistas, los aspirantes además de pasar al laboratorio lo pueden hacer a las siguientes salas: cofres, conocimiento, retos, apuestas, ascensos y comercio. Mientras el participante tenga tiradas mágicas podrá ir pasando de una de estas salas a otra y decidir donde utilizarlas.
En la sala de cofres los aspirantes pueden utilizar sus tiradas mágicas para abrir cofres dentro de los cuales se encuentras premios muy similares a los del laboratorio. De igual forma podrán conseguir: ascensos, tiradas, gemas, X2 y cartas.
En la sala de conocimiento los participantes podrán gastar hasta 5 de sus tiradas mágicas para conseguir: oro, poción o conocimiento. Por cada tirada empleada el participante recibirá una pregunta. Según el número de respuestas correctas al final de la serie de preguntas se podrán canjear por los elementos conseguidos. Por un acierto 1 elemento, por dos aciertos 3, por tres aciertos 6, por cuatro aciertos 10 y por cinco respuestas correctas 15.
La sala de retos permite al jugador que está en su turno retar a otro participante. El duelo tendrá un máximo de 5 preguntas. Si ambos jugadores aciertan la cuestión planteada recibirán una tirada mágica, mientras que si ambos fallan la perderán. Si uno da la respuesta correcta y otro falla, el acertante ganará dos tiradas mágicas que perderá su oponente. Si alguno de los jugadores se queda sin tiradas mágicas el duelo finaliza.
En la sala de apuestas el participante que tiene el turno puede seleccionar hasta un máximo de 5 oponentes. A todos se les planteará hasta un máximo de 5 preguntas y para cada pregunta el retador decidirá el valor de la apuesta entre una y tres tiradas mágicas. Los que acierten ganarán el valor de la apuesta realizada y los que fallen la perderán. Los jugadores que se queden sin tiradas dejarán de participar. Si el retador se queda sin tiradas la ronda se termina.
La sala de ascensos es la estancia en la que pagando dos tiradas mágicas y respondiendo correctamente a cinco preguntas los aspirantes consiguen un ascenso. Tienen un comodín que les permite cometer un fallo. Si no superan la prueba descienden una posición en su rango.
La última sala nueva es la sala de comercio. En ella el aspirante que tiene el turno podrá pagar una tirada mágica para que, durante su turno, se establezca por sorteo una nueva tabla de precios. Además podrá comprar oro, poción o conocimiento al precio en tiradas mágicas que esté establecido.
Otra consideración es que se eleva a 10 el número máximo de oro, poción y conocimiento que cada aspirante puede acumular en su marcador.
El objetivo sigue siendo alcanzar el máximo rango dentro de la jerarquía alquimista del juego y superar al resto de los aspirantes.
SCORM de valor numérico de un polinomio
Escrito por Emilio Pazo NúñezEste mes voy a compartir un SCORM correspondiente al tema de polinomios de tercero de ESO. Se trata de un ejercicio sobre el valor numérico de un polinomio, que puede resultar adecuado desde segundo de ESO hasta cuarto.
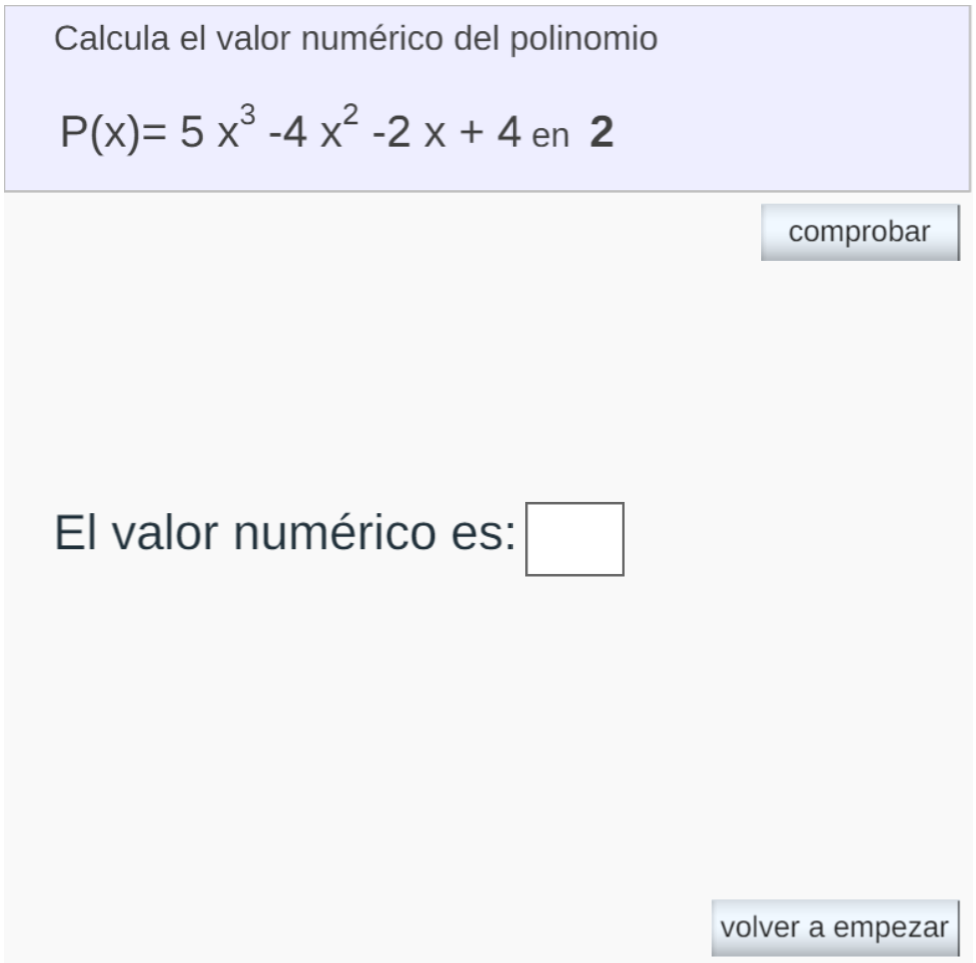
La escena original contiene 2 ejemplos y 3 ejercicios, mientras que en esta escena adaptada se han eliminado los ejemplos y los ejercicios deben realizarse por orden. Como es habitual, se añade un botón "enviar nota" que permite que se registre el resultado en la plataforma moodle en la que se inserta el SCORM. El primer ejercicio, más sencillo por ser el valor numérico para un número entero, se valora con un 30% de la nota, mientras que los dos restantes, un poco más complicados por ser el valor numérico para una fracción, se valoran con un 35%. Como en anteriores adaptaciones, también se añade un botón de "volver a empezar" que permite reiniciar el ejercicio sin tener que cerrarlo y volver a abrirlo, botón que desaparece si se alcanza la puntuación máxima.
Si algún lector está interesado en la adaptación de una escena en concreto, se agradece que lo indique en comentarios y se abordará en un próximo artículo.
Día Internacional de la Mujer y la Niña en la Ciencia con RED Descartes - 2022
Escrito por José Antonio Salgueiro GonzálezUn año más, desde RED Descartes queremos aportar nuestros recursos y colaboración para celebrar la efemérides del "Día Internacional de la Mujer y la Niña en la Ciencia", a la vez que animamos a programar y desarrollar actividades en el aula con nuestro alumnado para cumplir con los objetivos establecidos:
- Visibilizar el trabajo de las mujeres que se dedican a las áreas STEM (Science, Technology, Engineering and Mathematics), creando así referentes femeninos para la infancia que puedan contribuir a la elección de estas áreas como carreras profesionales.
- Conocer los diferentes factores que afectan a la situación actual de la mujer en las áreas STEM para fomentar prácticas que conduzcan a su eliminación y alcanzar la igualdad de género en el ámbito científico.

| JUEGO DIDÁCTICO SOBRE GRANDES CIENTÍFICAS |
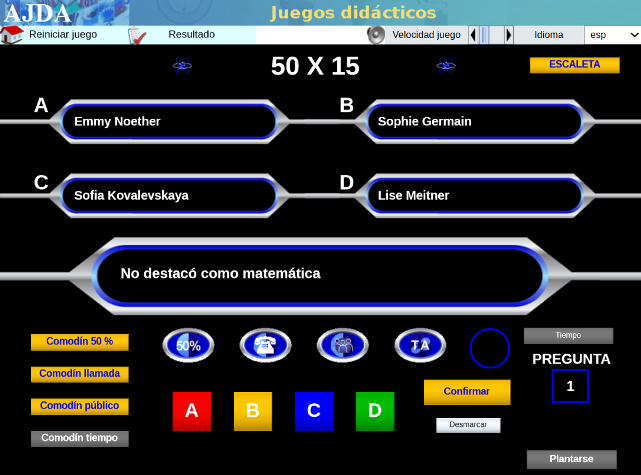
El juego es una de las estrategias didácticas de gran valor que motiva a nuestro alumnado y que se potencia con las tecnologías de la información y la comunicación. Así que os dejamos el que ha creado nuestro compañero Jesús M. Muñoz Calle, del proyecto Aplicación de Juegos Didácticos en el Aula, para difundir algunos de los decubrimientos y avances científicos gracias a la mujer, con algunas capturas de pantalla por si fueran necesarias. Es idóneo para organizar una pequeña competición en el aula proyectado desde la pizarra digital interactiva.
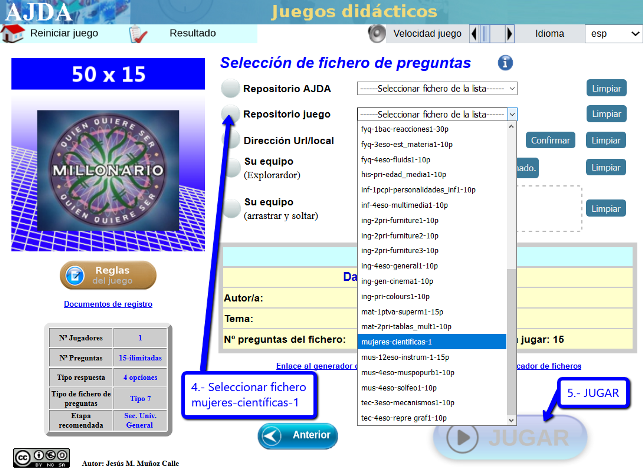
| LA MUJER EN LA CIENCIA |
"El personaje misterioso" es un programa de Radio Descartes conducido por Eva Perdiguero y Ángel Cabezudo con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Concretamente, tras la entrevista del invitado, que no se desvela, el escuchante debería conocer su nombre o bien tomar los datos que se aportan en la dramatización y tomarse un tiempo para averiguarlo consultando en la múltiple documentación que hoy día se encuentra disponible, principalmente en Internet o en libros divulgativos de Historia de las Matemáticas o de Matemáticos célebres, pasando a responder en un comentario del blog de nuestro portal. Pues bien, de este proyecto hemos seleccionado las siguientes entrevistas a grandes matemáticas de la historia, cuyas voces son interpretadas por científicas del ámbito educativo. Así, aportamos los siguientes recursos:
- Entrevista a Hipatia de Alejandría, interpretada por Eva Mª. Perdiguero Garzo, profesora de matemáticas.
- Entrevista a Sofía Kovalévskaya, interpretada por Marta Macho Stadler, matemática y divulgadora científica.
- Entrevista a Emmy Noether, interpretada por Elena Vázquez Abal, matemática y divulgadora científica.
- Entrevista a Ada Lovelace, interpretada por Montse Gelis Bosch, profesora de matemáticas.
- Entrevista a María Gaetana Agnesi, interpretada por Elena Ramírez Ezquerro, profesora de matemáticas.
Para descubrir al personaje misterioso, se publica un puzle creado con Descartes JS que incluye imágenes alusivas, alegóricas o de efemérides que descubren al personaje:
- Puzle dedicado a Hipatia de Alejandría
- Puzle dedicado a Sofía Kovalévskaya
- Puzle dedicado a Emmy Noether
- Puzle dedicado a Ada Lovelace
- Puzle dedicado a María Gaetana Agnesi
| CONTRIBUCIONES DE ALUMNAS A LA CIENCIA |
Son varios los proyectos difundidos desde el portal de RED Descartes donde las alumnas son protagonistas y divulgadoras de la ciencia, especialmente de la matemática. Así, hemos seleccionado con motivo del día 11 de febrero las siguientes contribuciones y aportaciones de alumnas a la ciencia, clasificadas por etapa educativa, con objeto de que puedan usarse en las pizarras digitales de las aulas, en los espacios virtuales de aprendizaje, abrir debates y plantear la actividad que cada docente determine.
| CIENTÍFICAS EN INFANTIL Y PRIMARIA |
- Color y cantidad. Pensamos juntos para resolver una situación
- Significado de perímetro
- Experiencia de pensamiento autónomo en resolver un problema. Alumna de 3 años
- Ángulo recto para construir un metro cuadrado en papel
- Alumnas de cuarto de primaria en la investigación y aprendizaje de capacidades y su expresión en lenguaje matemático
| CIENTÍFICAS EN SECUNDARIA |
- Antonia y Maite nos enseñan la aplicación de la maqueta en la semejanza de figuras
- Ángela y Cristina nos muestran la utilidad de la maqueta en el aprendizaje de la semejanza
- Alba y Ángela nos enseñan a discutir y resolver sistemas de ecuaciones con Descartes y herramientas tecnológicas
- Natalia y Celeste comunican y comparten ideas matemáticas con Descartes
- Carmen, divulga la simplificación de fracciones algebraicas y la suma de las mismas
- Rocío, divulga la resolución de una unidad liberada de PISA
- Virginia, María y Laura, divulgan una técnica de resolución de problemas
- María del Castillo e Irene, divulgan las operaciones con fracciones algebraicas
- María y Claudia entrevistan a Sofía Kovalévskaya, con su matrimonio de conveniencia para poder estudiar matemáticas.
- Mireia y María entrevistan y divulgan la obra de Sophie Germain, la primera mujer en acceder a la Academia de Ciencias de París.
- Antonia y Maite entrevistan y divulgan la vida y obra de Ada Lovelace, con su reflexión sobre la mujer en la ciencia y el techo de cristal.
- Clara, Ángela y Cristina, entrevistan y divulgan la vida y obra de Mary Cartwright, a quien conocí gracias a mis alumnas.
- María y Julia, entrevistan y divulgan la vida y obra de Mary Somerville, conocida como "La Reina de las ciencias del siglo XIX".
- Ángela y Alejandro, entrevistan y divulgan la vida y obra de Euclides
| CIENTÍFICAS EN BACHILLERATO |
- María, divulga la resolución de triángulos rectángulos
- Claudia y María, divulgan la simplificación de expresiones trigonométricas de cociente
- Margarita y María, divulgan la simplificación de expresiones trigonométricas de cociente
- Ángela y Alba, ponen a prueba tus conocimientos de Matemáticas-1
- Laura y Ángela, ponen a prueba tus conocimientos de Matemáticas-1
- Zuleima y Raquel, ponen a prueba tus conocimientos de Matemáticas-1
- Ana y Virginia, ponen a prueba tus conocimientos de Matemáticas-1
- María y Alba, ponen a prueba tus conocimientos de Matemáticas-1
- Lucía e Ismael, ponen a prueba tus conocimientos de Matemáticas-1
- Ángela y Laura y ponen a prueba tus conocimientos de Matemáticas-2
- Joana y Ana ponen a prueba tus conocimientos de Matemáticas-2
- Aurora, Alba, Ángela y Teresa recrean la importancia de la seguridad al desarrollar experiencias en el laboratorio
- Carmen, Joana, Beatriz y Ángela muestran, de forma desenfada, las normas en el laboratorio de Química.
| CIENTÍFICAS EN LA UNIVERSIDAD |
- Sofía, Marcos y Juan Luis nos enseñan a calcular el volumen de un cono por integrales triples.
- Daniela, Beatriz y Jonathan nos muestran algunas aplicaciones de las coordenadas esféricas.
- Tania y Samuel nos enseñan a cambiar de coordenadas cartesianas a polares y cilíndricas.
- Lucía y Alicia nos presentan el cálculo de áreas de figuras planas utilizando integrales dobles.
- Daniela, Beatriz y Jonathan calculan el aforo de un recinto para conciertos.
- Lucía y Alicia nos explican cómo calcular el volumen del Atomium de Bruselas.
- Almudena y Clara nos enseñan a calcular el gradiente de un campo escalar y el uso correcto del operador nabla.
- Clara y Almudena nos muestran el rotacional y la divergencia de un campo vectorial.
- Tania y Samuel nos presentan la resolución de ecuaciones diferenciales con variables separables.
- Andrea y Andrés nos enseñan la función delta de Dirac, sus propiedades y algunas aplicaciones.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)





 CONTACTO
CONTACTO
