| 1 |
 |
Modelo de la Tierra |
Introducción a la Geodesia como ciencia que estudia la forma del planeta Tierra (elipsoide, geoide y superficie topográfica). Conocer los tres tipos de coordenadas terrestres: geocéntricas, geodésicas y geográficas. |
|
||||
|
|
||||||||
| 2 |
 |
Esfera como superficie de revolución |
Una esfera puede obtenerse al girar una semicircunferencia alrededor de uno de sus diámetros. Consecuentemente se dice que es una superficie de revolución. Se amplia la situación al esferoide (caso particular de los elipsoides)toros, toros elípticos y toroides. Finalmente se exponen dos modelos de la Tierra. |
|
||||
|
|
||||||||
| 3 |
 |
Geodésicas en la esfera |
Se busca determinar cuál es el camino mínimo que hay que recorrer sobre una esfera para desplazarse entre dos puntos de ella. La distancia mínima se corresponde con la mayor circunferencia que une esos puntos. El radio y el centro de esa circunferencia máxima coincide con el radio y centro de la esfera. Al circulo determinado por dicha circunferencia se le denomina "circulo máximo". |
Escena: Determinación del círculo máximo como geodésica. | ||||
|
|
||||||||
| 4 |
 |
Loxódromas en la esfera |
Si se parte de un punto de la superficie de una esfera y se desplaza manteniendo un ángulo constante con los meridianos (rumbo fijo) se obtiene una trayectoria, una curva, denominada loxódroma (de loxos: inclinado y dromo: camino). Las loxódromas no coinciden con las geodésicas de la esfera, por tanto no proporcionan el camino de longitud mínima. |
|
||||
|
|
||||||||
| 5 |
 |
Ejemplos superficies revolución |
Se muestran diferentes ejemplos de superficies de revolución. Estas se obtienen al girar una curva plana alrededor de una recta o eje de revolución. Se obtienen los paralelos o intersección de la superficie con planos perpendiculares al eje y los meridianos o intersección con un haz de planos secantes de arista el eje. |
Escena: Algunas superficies de revolución. Meridianos y paralelos. Coordenadas | ||||
|
|
||||||||
| 6 |
 |
Construyo mis superficies de revolución |
Con este objeto se puede construir cualquier superficie de revolución sin más que definir su generatriz. Una misma definición permite construir diferentes superficies ya que se puede elegir el número de segmentos a considerar en la representación gráfica de la generatriz, así como el intervalo de definición y el rango de representación. |
Escena: Construye tu superficie de revolución. Meridianos y paralelos. Coordenadas | ||||
|
|
||||||||
| 7 |
 |
Triángulos en la Geometría Euclídea |
Se enuncian los cinco postulados de Euclídes. Se muestra tanto en el plano como en una superficie desarrollable (el cilindro) que en la Geometría euclídea los tres ángulos de un triángulo suman 180º. |
|
||||
|
|
||||||||
| 8 |
 |
Ángulo diedro |
Se busca mostrar que la medida del ángulo diedro es la medida del ángulo rectilíneo formado por dos semirrectas con vértice común en la arista del diedro y perpendiculares a ésta. |
|
||||
|
|
||||||||
| 9 |
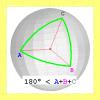 |
Triángulos en la Geometría Elíptica |
Se muestra que la suma de los ángulos de un triángulo esférico suman más de 180º y menos de 540º y que la suma de los lados de un triángulo esférico es menor de 2πR (o longitud de un círculo máximo), donde R es el radio de la esfera. Los triángulos esféricos son la porción de superficie esférica delimitada por tres geodésicas que se intersecan entre sí. |
|
||||
|
|
||||||||
| 10 |
 |
Geodésicas en el disco de Poincaré |
En este objeto se muestra la existencia de otra geometría no euclídea. El disco de Poincaré es un ejemplo de geometría plana hiperbólica. Sobre el círculo abierto unidad (no incluye la circunferencia frontera) se considera una métrica donde las geodésicas son diámetros o círculos ortogonales a la frontera. Se muestran las geodésicas, el paralelismo y cómo no se verifica el quinto postulado de Euclides. |
|
||||
|
| ||||||||
| 11 |
 |
Triángulos en el disco de Poincaré |
En este objeto se muestra como se define el ángulo determinado por dos curvas en un punto común y se determina la suma de los ángulos de un triángulo en el disco de Poincaré comprobándose que ésta es siempre inferior a 180º, lo cual contradice a lo conocido en la geometría Euclidea plana. Surge otra geometría que se denomina no euclídea . |
|
||||
|
|
||||||||
| 12 |
 |
Un patrón para medir |
Medir
es comparar una magnitud con otra, tomada como referencia,
denominada patrón y expresar cuántas veces la contiene. A lo largo de
la historia la comunidad internacional ha intentado ponerse de acuerdo
para obtener un patrón del METRO. Haremos un recorrido por la historia
y nos detendremos en un patrón peculiar, el PÉNDULO |
|
||||
|
|
||||||||
| 13 |
 |
El metro y el cuadrante de meridiano |
El sistema métrico decimal optó por definir el metro a partir de un elemento universal, propiedad de la Humanidad: La Tierra. El metro es la diezmillonésima parte del cuadrante de un meridiano terrestre. La alternativa de uso del péndulo no fue adoptada. |
Escena: El metro a partir del cuadrante terrestre. Kilómetros y millas | ||||
|
|
||||||||
| 14 |
 |
Sistema métrico decimal |
Aprendizaje de los Factores, Prefijos y Símbolos utilizados en el Sistema Internacional (S. I.) para designar múltiplos y submúltiplos. Orden de magnitud. Prácticas de cambio de unidades, paso de forma compleja a forma incompleja, ordenación de múltiplos y submúltiplos. |
|
||||
|
|
||||||||
| 15 |
 |
Unidades de longitud |
Aprendizaje de las unidades de longitud del Sistema Internacional (S.I.). Múltiplos y submúltiplos. Factores, Prefijos y Símbolos. Orden de magnitud. Prácticas de cambio de unidades, paso de forma compleja a forma incompleja, ordenación de múltiplos y submúltiplos. |
|
||||
|
|
||||||||
| 16 |
 |
Unidades de superficie |
Aprendizaje de las unidades de superficie del Sistema Internacional (S.I.). Múltiplos y submúltiplos. Factores, Prefijos y Símbolos. Orden de magnitud. Prácticas de cambio de unidades, paso de forma compleja a forma incompleja, ordenación de múltiplos y submúltiplos. |
|
||||
|
|
||||||||
| 17 |
 |
Unidades de volumen |
Aprendizaje de las unidades de volumen del Sistema Internacional (S.I.). Múltiplos y submúltiplos. Factores, Prefijos y Símbolos. Orden de magnitud. Prácticas de cambio de unidades, paso de forma compleja a forma incompleja, ordenación de múltiplos y submúltiplos. |
|
||||
|
|
||||||||
| 18 |
 |
Unidades de capacidad |
Aprendizaje de las unidades de capacidad. Múltiplos y submúltiplos. Factores, Prefijos y Símbolos. Orden de magnitud. Prácticas de cambio de unidades, paso de forma compleja a forma incompleja, ordenación de múltiplos y submúltiplos. |
|
||||
|
|
||||||||
| 19 |
 |
Unidades de masa |
Aprendizaje de las unidades de masa del Sistema Internacional (S.I.). Múltiplos y submúltiplos. Factores, Prefijos y Símbolos. Orden de magnitud. Prácticas de cambio de unidades, paso de forma compleja a forma incompleja, ordenación de múltiplos y submúltiplos. |
|
||||
|
|
||||||||
| 20 |
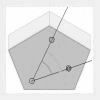 |
Medir ángulos |
Medición de ángulos. Comprender la definición de radián. Clasificación de ángulos. Utilización del goniómetro para estudiar las propiedades de los polígonos regulares y los ángulos diedros. |
|
||||
|
|
||||||||
| 21 |
 |
Medir longitudes |
La operatividad con números decimales y el concepto de error intrínseco a cualquier proceso de medida, constituyen objetivos fundamentales que deben consolidarse plenamente. |
Escena: Medición de longitudes. Errores | ||||
|
|
||||||||
| 22 |
 |
Medir superficies |
La triangulación constituye uno de las primeros y más sencillos métodos para medir superficies tanto regulares como irregulares. |
Escena: Medición de superficies. Errores. | ||||
|
|
||||||||
| 23 |
 |
Principio de Cavalieri |
Basándonos en el principio de Cavalieri simplificaremos tanto el cálculo del volumen de prismas y pirámides como el área de figuras planas. |
|
||||
|
|
||||||||
| 24 |
 |
Curvas de nivel |
Los mapas topográficos constituyen una herramienta sencilla y útil que conviene saber interpretar, al menos en sus aspectos fundamentales. El trazado de un determinado perfil ayuda de forma fundamental en el conocimiento real de una determinada geografía. |
Escena: Trazado de perfiles topográficos a partir de las curvas de nivel. | ||||
|
|
||||||||
| 25 |
 |
Proporciones |
El estudio de proporciones es de aplicación en la arquitectura, escultura, pintura y en el arte en general. Las proporcionalidad surge de la naturaleza. Entre las proporciones más significativas están las denominadas áurea o divina y cordobesa o humana. |
|
||||
|
|
||||||||
| 26 |
 |
Extremos condicionados. Áreas. |
Se plantean problemas de cálculo de extremos condicionados en áreas. |
|
||||
|
|
||||||||
| 27 |
 |
Extremos condicionados. Volúmenes. |
Se plantean problemas de cálculo de extremos condicionados en volúmenes de prismas y cilindros. |
|
||||
|
|
||||||||
| 28 |
 |
Paradoja superficies y volúmenes |
La Trompeta de Gabriel constituye uno de los ejemplos visuales más interesantes de figura con superficie infinita que encierra sin embargo un volumen finito. Históricamente ha supuesto un ejercicio matemático y filosófico interesante que muchos han catalogado de paradoja. |
Escena: Paradoja de superficie infinita y volumen finito.. | ||||
|
|
||||||||
| 29 |
 |
Regresión lineal |
El ajuste de una nube de puntos mediante una recta constituye un problema fundamental en un contexto de dependencia lineal entre una variable estadística bidimensional. Uno de los métodos empleados con más eficacia es el conocido como "ajuste mediante mínimos cuadrados". |
Escena: Regresión lineal de una nube aleatoria de puntos. | ||||
|
|
||||||||
| 30 |
 |
"Outlier" |
Uno de las primeras acciones que se realizan en cualquier estudio estadístico es la depuración de los datos, localizando y decidiendo si los elementos anómalos "outliers", deben tenerse en cuenta en la realización del estudio o no. En este objeto se analiza la influencia que puede tener la variación de un solo dato en un análisis estadístico. |
Escena: Influencia que puede tener la variación de un solo dato en un análisis estadístico. | ||||
|
|
||||||||
| 31 |
 |
Medidas estadísticas Sensibilidad. |
La sensibilidad o robustez de las medidas estadísticas clásicas frente a pequeños o no tan pequeños cambios de algún dato constituye un objeto de discusión con bastantes posibilidades de debate e incluso propuestas de pequeñas conjeturas. | Escena: Sensibilidad de las medidas estadísticas al variar un dato. | ||||
|
|
||||||||
| 32 |
 |
Medidas estadísticas Caso continuo |
La sensibilidad o robustez de las medidas estadísticas clásicas frente a pequeños o no tan pequeños cambios en la frecuencia de alguno de los intervalos constituye un objeto de discusión con bastantes posibilidades de debate e incluso propuestas de pequeñas conjeturas. | Escena: Sensibilidad de las medidas estadísticas al variar la frecuencia en un intervalo. | ||||
|
|
||||||||
| 33 |
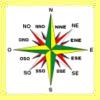 |
Rosa de los vientos |
Con este objeto se persigue la comprensión de los diferentes rumbos de navegación y uso de escalas sobre mapas, así como su aplicación para la resolución de determinados problemas de orientación y localización. |
|
||||
|
|
||||||||
| 34 |
 |
Proyección cilíndrica |
Se muestra como se efectúa la proyección cartográfica de una superficie esférica en una superficie plana. La utilización de una superficie desarrollable como el cilindro conduce a la denominada proyección cilíndrica. |
|
||||
|
|
||||||||
| 35 |
 |
Proyección de Mercator |
Se presenta la denominada proyección de Mercator. Este sistema de proyección, basado en la proyección cilíndrica, permite corregir en parte la alta distorsión que presentan las zonas situadas muy al norte o muy al sur. |
|
||||
|
|
||||||||
| 36 |
 |
Lóxodromas y Geodésicas en Mercator |
Con este objeto se comparan dos trayectorias con las que pueden unirse dos puntos situados sobre la esfera terrestre. El camino más corto no coincide con la loxódroma o camino a través de un rumbo (línea recta en la proyección Mercator) sino a través del círculo máximo que es la geodésica de la esfera. |
Escena: Comparación de loxódromas y círculo máximo | ||||
|
|
||||||||
| 37 |
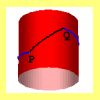 |
Geodésicas y loxódromas en un cilindro |
Se busca determinar cuál es el camino mínimo que hay que recorrer sobre la superficie lateral de un cilindro recto. Al ser una superficie desarrollable es posible reducir el problema tridimensional a uno bidimensional. |
|
||||
|
|
||||||||
| 38 |
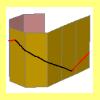 |
Geodésicas y loxódromas en un prisma |
Se busca determinar cuál es el camino mínimo que hay que recorrer para desplazarse entre dos puntos situados sobre la superficie lateral de un prisma recto regular. Al ser una superficie desarrollable es posible reducir el problema tridimensional a uno bidimensional. |
|
||||
|
|
||||||||
| 39 |
 |
Geodésicas en el cubo |
Se busca determinar cuál es el camino mínimo que hay que recorrer sobre un cubo para desplazarse entre dos puntos situados en sendas caras contiguas. Al ser una superficie desarrollable es posible reducir el problema tridimensional a uno bidimensional. |
|
||||
|
|
||||||||
| 40 |
 |
Cilindro como superficie de revolución |
Un cilindro puede obtenerse al girar un segmento rectilíneo alrededor de una recta paralela a él denominada eje. Consecuentemente se dice que es una superficie de revolución. Se analizan las propiedades, un posible sistema de referencia, la asignación de unidades a éste y un mapa del cilindro. |
|
||||
|
|
||||||||
| 41 |
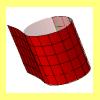 |
Generalización del cilindro |
El cilindro es un sólido generado por un segmento rectilíneo al girar sobre un eje, el extremo de ese segmento describe una circunferencia. Aquí se generaliza el concepto de cilindro al considerar que la generatriz puede describir cualquier curva plana. |
Escena: Generalización de un cilindro. Paralelos y meridianos. Desarrollo plano. | ||||
|
|
||||||||
| 42 |
 |
Ejemplos Cilindros generalizados |
Se muestran diferentes ejemplos de cilindros generalizados. Estos se obtienen al describir un segmento rectilíneo una curva plana. que puede ser tanto abierta como cerrada. |
Escena: Ejemplos de cilindros generalizados. Paralelos y meridianos. Desarrollo plano. | ||||
|
|
||||||||
| 43 |
 |
Construyo mis Cilindros |
Con este objeto se puede construir cualquier cilindro generalizado sin más que definir la curva base del mismo. Una misma definición permite construir diferentes cilindros ya que se puede elegir el número de segmentos a considerar en la representación gráfica de la base. |
Escena:
Construye tus cilindros generalizados. Paralelos y
meridianos. Desarrollo plano.
|
||||
|
|
||||||||
| 44 |
 |
Proyección Cónica |
En este objeto se explica el modelo de proyección cónica. La superficie del globo terrestre se proyecta sobre un cono tangente a la esfera en un determinado paralelo y se estudian las distorsiones producidas. |
|
||||
|
|
||||||||
| 45 |
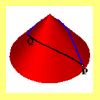 |
Geodésicas en un cono |
Se busca determinar cuál es el camino mínimo que hay que recorrer sobre la superficie lateral de un cono recto. Al ser una superficie desarrollable es posible reducir el problema tridimensional a uno bidimensional. |
|
||||
|
|
||||||||
| 46 |
 |
Loxódromas en el cono |
Si se parte de un punto de la superficie de un cono y se desplaza manteniendo un ángulo constante con los meridianos o generatrices del mismo, es decir si se mantiene un rumbo fijo, se obtiene una trayectoria, una curva, denominada loxódroma (de loxos: inclinado y dromo: camino). Las loxódromas no coinciden con las geodésicas en el cono. |
|
||||
|
|
||||||||
| 47 |
 |
Geodésicas en una pirámide |
Se busca determinar cuál es el camino mínimo que hay que recorrer para desplazarse entre dos puntos situados sobre la superficie lateral de una pirámide recta regular. Al ser una superficie desarrollable es posible reducir el problema tridimensional a uno bidimensional. |
|
||||
|
|
||||||||
| 48 |
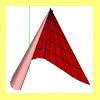 |
Conos generalizados |
El cono es un sólido generado por un segmento rectilíneo que mantiene uno de sus extremos fijo (vértice) y el otro describe una circunferencia (curva directriz). Aquí se generaliza el concepto de cono al considerar que la curva directriz puede ser cualquier curva plana. |
Escena: Generalización de un cono. Paralelos y meridianos. Desarrollo plano. | ||||
|
|
||||||||
| 49 |
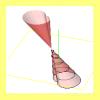 |
Ejemplos Conos generalizados |
Se muestran diferentes ejemplos de conos generalizados. Estos se obtienen al describir el extremo de un segmento rectilíneo una curva plana (directriz) mientras que el otro (vértice) queda fijo. La curva directriz puede ser tanto abierta como cerrada. |
Escena: Generalización de un cono. Paralelos y meridianos. Desarrollo plano. | ||||
|
|
||||||||
| 50 |
 |
Construyo mis conos |
Con este objeto se puede construir cualquier cono generalizado sin más que definir la curva directriz del mismo. Una misma definición permite construir diferentes conos ya que se puede elegir el número de segmentos a considerar en la representación gráfica de la directriz. |
Escena:
Construye tus conos generalizados. Paralelos y
meridianos. Desarrollo plano.
|
||||
|
|