En este artículo se describen y clasifican las superficies regladas desarrollables poniendo de manifiesto que éstas son cilindros, conos y superficies tangenciales. Y, mediante el uso de Descartes, se permite al usuario abordar la construcción virtual de "su" cilindro y cono personalizado, pero también se le da la posibilidad de convertirlo en un objeto tridimensional tangible sin más que proceder a la obtención automática de su desarrollo plano y, mediante su impresión en papel, proceder a su construcción.
Superficies regladas desarrollables
Una superficie es reglada si está constituida por una familia de rectas. Todas estas superficies se pueden parametrizar como:
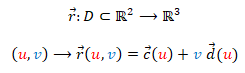 (1)
(1)
donde 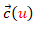 y
y 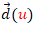 son curvas en el espacio tridimensional. La primera es la curva base o curva directriz y la segunda es el vector director de cada una de las rectas (generatriz). Efectivamente, fijado un valor del parámetro u puede observarse que la expresión obtenida es la ecuacion de una recta y, variando u, geométricamente lo que se puede interpretar es que se va recorriendo cada punto de la curva base
son curvas en el espacio tridimensional. La primera es la curva base o curva directriz y la segunda es el vector director de cada una de las rectas (generatriz). Efectivamente, fijado un valor del parámetro u puede observarse que la expresión obtenida es la ecuacion de una recta y, variando u, geométricamente lo que se puede interpretar es que se va recorriendo cada punto de la curva base 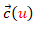 y por él pasa una recta cuya dirección viene dada por
y por él pasa una recta cuya dirección viene dada por 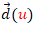 .
.
También puede expresarse de manera equivalente como:
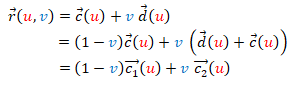 (2)
(2)
que algebraicamente representa, para cada valor de u, a una recta (o un segmento si consideramos 0 ≤ v ≤ 1), pero en este caso lo que se pone de manifiesto es que esa recta se apoya en un punto de la curva 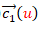 y en otro de la
y en otro de la 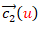 .
.
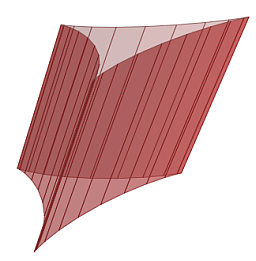
El ejemplo más simple de superficie reglada es un plano, pero entre otras, también lo son los cilindros, los conos, la banda de Moebius, el hiperboloide, etc.
 |
 |
| Cilindro generalizado | Cono generalizado |
 |
 |
| Banda de Möbius | Hiperboloide |
Una herramienta matemática que permite caracterizar la curvatura de cualquier superficie regular es la denominada curvatura de Gauss, y se verifica que dicha curvatura es invariante por isometrías. Todas las superficies regladas cumplen que su curvatura de Gauss es menor o igual que cero y, en particular, que la curvatura de Gauss de un plano es identicamente nula. En base a lo anterior, todas las superficies regladas que tienen curvatura cero son isométricas con el plano y son denominadas como superficies desarrollables ya que, consecuentemente, pueden construirse a partir de su desarrollo plano.
En la parametrización (1) la condición de curvatura nula equivale a que el denominado parámetro de distribución sea nulo, y éste viene dado por:
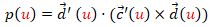 (3)
(3)
o en el caso de la parametrización (2) como:
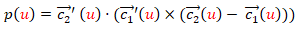 (4)
(4)
De (4) se observa que para que la superficie reglada sea desarrollable tiene que ocurrir que para todo u el vector tangente a la curva 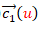 , el vector tangente a
, el vector tangente a 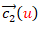 y el vector director de la recta que une a ambas curvas sean coplanarios al ser el producto mixto de los tres cero, o dicho de otra forma que el plano tangente es constante lo largo de cada recta generatriz.
y el vector director de la recta que une a ambas curvas sean coplanarios al ser el producto mixto de los tres cero, o dicho de otra forma que el plano tangente es constante lo largo de cada recta generatriz.
Pero un análisis más detenido de cuándo es identicamente nulo el parámetro de distribución nos puede permitir clasificar a las superficies desarrollables. Así en la expresión (3):
- Si
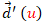 es identicamente nulo, entonces
es identicamente nulo, entonces 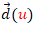 es un vector constante, es decir que todas las rectas tienen la misma dirección y la superficie es un cilindro generalizado de ecuación
es un vector constante, es decir que todas las rectas tienen la misma dirección y la superficie es un cilindro generalizado de ecuación 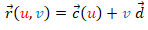 .
. - Si
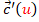 es idénticamente nulo, entonces
es idénticamente nulo, entonces 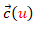 es el vector de posición de un punto V y la superficie desarrollable es un cono generalizado de vértice V, cuya ecuación sería
es el vector de posición de un punto V y la superficie desarrollable es un cono generalizado de vértice V, cuya ecuación sería 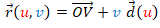 . También puede expresarse en función de una curva base como
. También puede expresarse en función de una curva base como 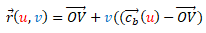 .
. - En cualquier otro caso se demuestra que es una superficie tangencial, que mediante un cambio de parámetro se puede expresar como
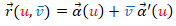 .
.
- Si
Superficies desarrollables con Descartes
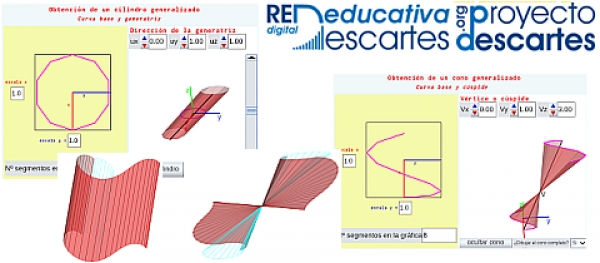
En el proyecto "El metro: patrón inexacto para medir exactamente", que en el año 2004 contó con una ayuda de la Junta de Andalucía (España) para la elaboración de materiales y recursos educativos digitales, desarrollamos con Descartes en su versión Java algunos objetos educativos interactivos sobre conos y cilindros generalizados incluyendo la posibilidad de obtener su desarrollo plano. En este año 2020 hemos procedido a adaptarlos a DescartesJS y a mejorar sus posibilidades, en particular en lo relativo a forma de obtener ese desarrollo plano, a incluir la posibilidad de su impresión y consecuentemente a la posibilidad de su reproducción tangible tridimensional. Estos recursos actualizados están publicados en el subproyecto "misceláneas" de la RED Descartes y los enlazamos a continuación aquí en dos triadas de imágenes que respectivamente se corresponden con cilindros y conos generalizados.
En la primera triada correspondiente a los cilindros tenemos:
- "Cilindro generalizado" donde se muestra la construcción de un cilindro tomando como curva base una elipse y en la que podemos cambiar la dirección de la recta generatriz. La escena permite reproducir la generación del cilindro mediante desplazamiento de la generatriz sobre la curva base; simular y obtener el desarrollo plano; imprimir dicho desarrollo y el de las bases del cilindro. Adicionalmente, dado el contexto en el que se desarrolló originalmente esta escena —el metro—, se puede obtener un sistema de referencia basado en meridianos y paralelos.
- "Ejemplos de cilindros generalizados" donde se puede elegir diferentes curvas base (circunferencia, elipse, parábola, rama de hipérbola, segmento, cardiode, deltoide, bifolium, astroide, bicircular) y reproducir las acciones indicadas en la escena anterior.
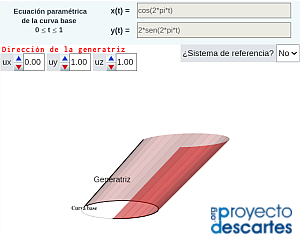
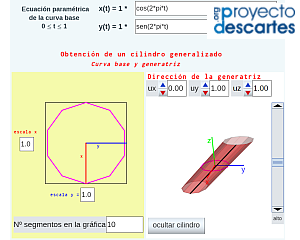
- "Construyo mis cilindros" que como indica el título permite al usuario definir la curva base en coordenadas paramétricas y la dirección de la generatriz que desee y con ellas construir su cilindro generalizado. De nuevo puede realizar de manera virtual interactiva las acciones ya indicadas, pero también procediendo a la impresión del desarrollo pasar a disponer de la versión tangible de "su" cilindro. Para cada curva base cambiando el número de segmentos que se desean considerar en la representación se obtienen diferentes cilindros, para simular el caso continuo basta seleccionar un número de segmentos suficientemente elevado.
 |
 |
 |
| Cilindro generalizado | Ejemplos de cilindros generalizados | Construyo mis cilindros |
De manera análoga en la triada correspondiente a los conos generalizados tenemos:
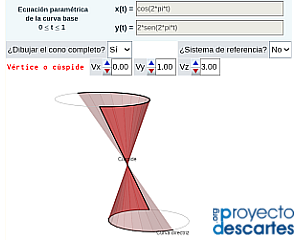
- "Cono generalizado" en el que se muestra la construcción de un cono tomando como curva base una elipse y en la que podemos cambiar su vértice. La escena interactiva permite reproducir la generación del cono mediante desplazamiento de la generatriz sobre la curva base; visualizar el cono completo; simular y obtener el desarrollo plano; imprimir dicho desarrollo y el de la base del cono. Adicionalmente, dado el contexto en el que se desarrolló originalmente esta escena —el metro—, se puede obtener un sistema de referencia basado en meridianos y paralelos.
- "Ejemplos de conos generalizados" donde se puede elegir diferentes curvas base (las mismas que en el caso de los cilindros) y reproducir las acciones indicadas en la escena anterior.
- "Construyo mis conos" que permite al usuario definir la curva base y el vértice y construir su cono generalizado tanto virtual como tangible..
 |
 |
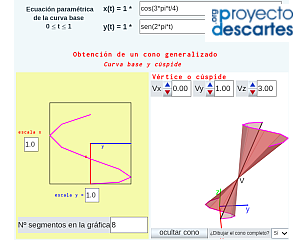 |
| Cono generalizado | Ejemplos de conos generalizados | Construyo mis conos |
En estos objetos interactivos se ha considerado que la curva base es una curva plana, así pues, he de ponerme la tarea de incorporar la tridimensionalidad de la curva base y presentarlo en un próximo artículo en este blog. Y, adicionalmente, este trabajo debería incoporar el caso de superficies tangenciales que implictamente, a priori, entraña cierta dificultad si se deja libertad de definición al usuario, pero sobre ello ya hablaremos.
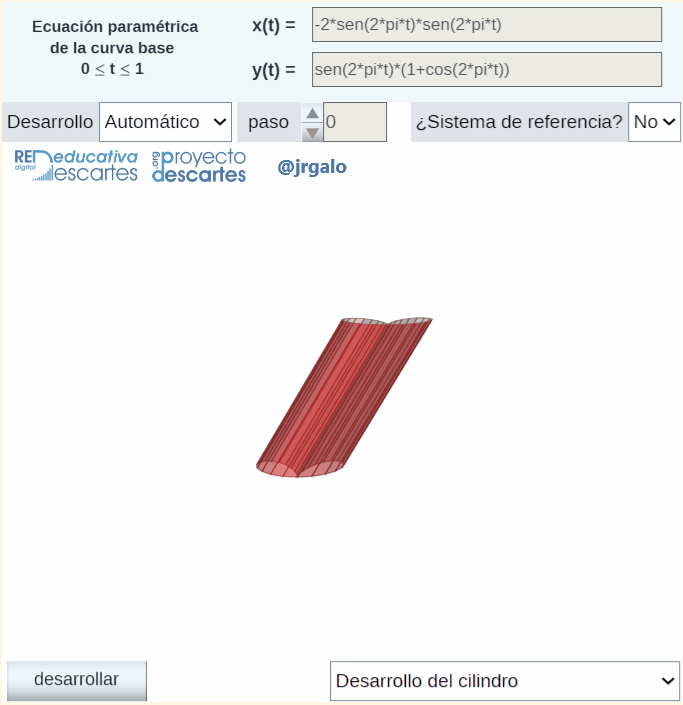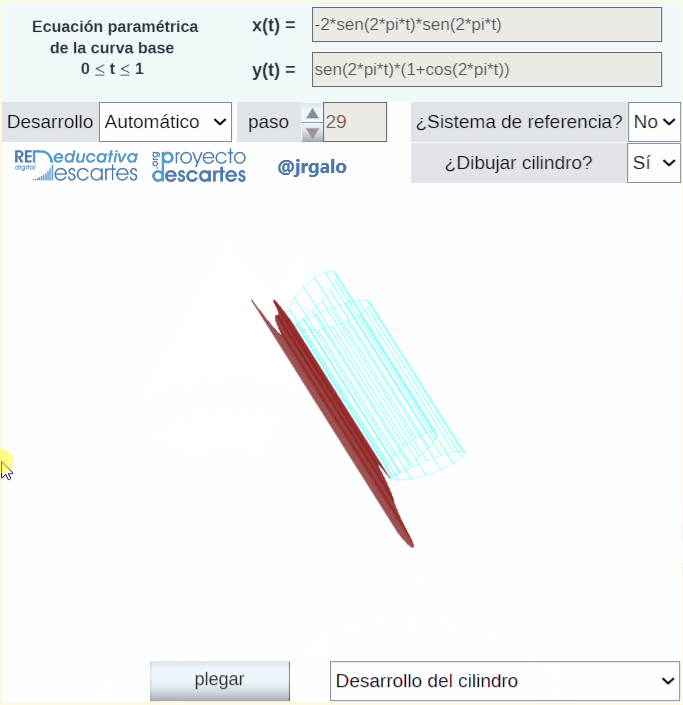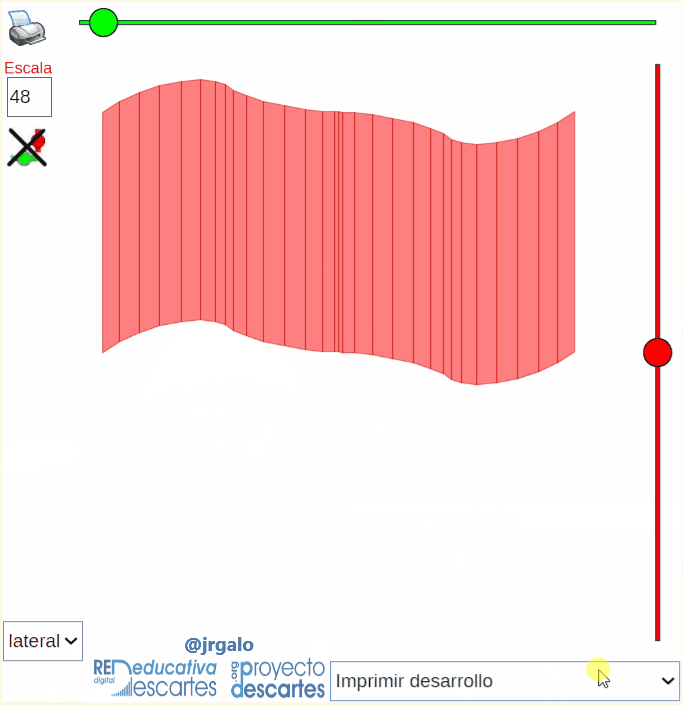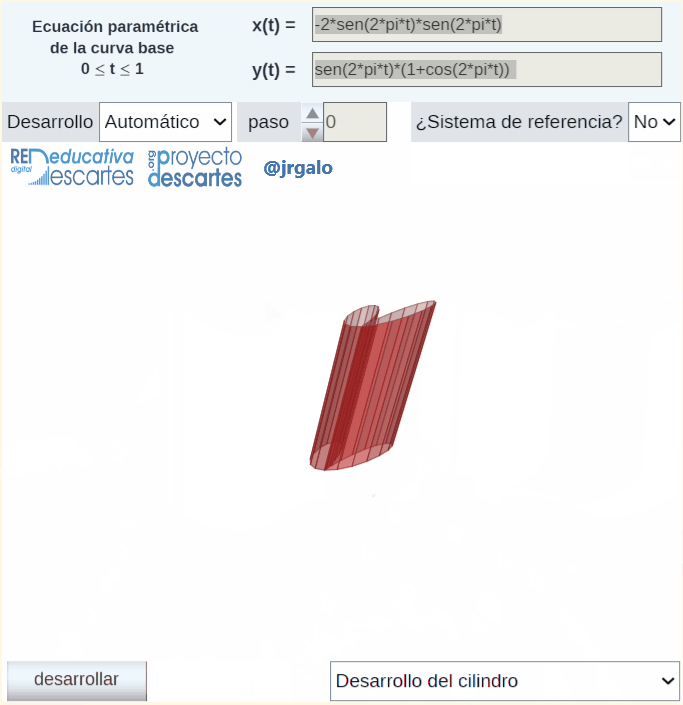
Finalizo reseñando que para la obtención automática y animada del desarrollo plano del cilindro y el cono se aplica la rotación de Rodrigues descrita en un artículo anterior de este blog. Lo que se hace es plantearlo como el desarrollo plano de un prisma o una pirámide que se ajuste suficientemente al cilindro o cono dado. En la animación siguiente se refleja el desarrollo plano de un cilindro generalizado en el que su base es la curva denominada bifolium.
Pulsa sobre la imagen para ampliarla
Bibliografía
Lucas, E. (2017). Superficies regladas [Trabajo fin de grado]. Universidad de Murcia.
Rosado, E (2010). Superficies regladas [Apuntes docentes]. Universidad Politécnica Madrid.


 CONTACTO
CONTACTO


