Amigos cartesianos
Fondo Editorial RED Descartes
Córdoba (España)
2023
Título de la obra:
Ildefonso Fernández Trujillo
¡in memoriam!
Autores:
Amigos cartesianos
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Imagen portada: Perfil de Ildefonso en la red social WhatsApp.
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-80-6
Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Ildefonso y colegas de la Red Educativa Digital Descartes.
Es aciago tener que escribir la "elegía" de un colega, de un compañero, de un amigo. ¡Ojalá fuéramos latinos clásicos y el motivo de ésta fuera por una causa placentera! Pero, ¡no! ¡no es así! y ni siquiera podemos imitar a Pablo Neruda y comenzar diciendo:
PUEDO escribir los versos más tristes esta noche...,
pues la rima se queda ahogada en la garganta.
Y al no poder hilar los sentimientos en palabras, sólo nos queda subir a las ondas armoniosas que fueron y siguen siendo agitadas magistralmente por nuestro excelso poeta Miguel Hernández, y leyendo pausada y detenidamente sus sentidos y bellos versos Acceso a la versión musical del cantautor Joan Manuel Serrat ., servirnos de ellos para portar nuestras aflicciones y penas. Y si acaso, modestamente, permitirnos parafrasear su dedicatoria:
En Móstoles, su pueblo adoptivo, se nos ha muerto como del rayo Ildefonso, con quien tanto queríamos
Nuestro recuerdo sólo puede abarcar un periodo corto de su vida, pues fue en 2008, hace quince años, cuando se incorporó al equipo de colaboradores del proyecto Descartes. No obstante, también podemos dar ciertas pinceladas anteriores que proceden del conocimiento adquirido sobre él, sobre su carácter y sobre su forma de ser y actuar, en el intercambio de correos electrónicos —soporte principal en la relación mantenida— y de esos contados momentos presenciales que pudimos manterner en reuniones esporádicas realizadas durante esos años. También su querida familia, su esposa Alicia Isabel y sus cinco hijos: Diego, Homero, Antonio, Carlos y Adora, han compartido con nosotros algunas pinceladas adicionales que nos han permitido aglutinar en un todo las facetas antes conocidas.
Por circunstancias familiares su trayectoria vital se inició en Teruel (Aragón), era mañico de nacimiento y, aunque allí solamente vivió su primer año y medio, ciertamente ese apelativo le impregnó dado que efectivamente fue magno, grande, y también era persona de buen querer Etimológicamente maño procede del lat. magnus y en Aragón maño se usa como expresión de cariño entre personas que se quieren bien..
Sus ascentros compartían alma cordobesa, de Montoro y de Priego, y al quedar huérfano a tan temprana edad regresó con su madre desde Teruel a tierras cordobesas, a un cortijo en la ciudad de Montilla.
Al cumplir ocho años partieron hacia Madrid donde estudió y desarrolló su vida laboral. Y en esa ciudad de acogida que es Madrid
y sus pueblos adláteres, entre ellos Móstoles donde residió, —que son todos lugares interculturales donde la vida te matiza, te hace, donde se diluyen las esencias, pero no se pierden—
terminó de conformar su característica personalidad que estaba impregnada de paciencia, humildad, sencillez, flexibilidad, generosidad, solidaridad, responsa-bilidad, tenacidad... esencialmente rebosante de afabilidad. Y teniendo que destacar que era ¡intensamente matemático!, no sólo por su formación en esta Ciencia, si no porque en él se hacía majestuosamente patente el significado etimológico del término μαθηματικος (mathematikós) Puede consultarse un detallado estudio etimológico en Godínez Cabrera, H. F. (1997), Una Relación Breve y Sumaria sobre el Origen y Evolución del Significado de la palabra Matemática Revista Educación Matemática, Vol. 9 No. 3, pp. 44-51. Aquí, Godínez indica:
"El texto de Platón recién citado, y otros que en su contexto tienen la palabra μαθηματικος, —así como el significado mismo del sufijo ικος, el cual es aptitud— nos dan elementos para afirmar que etimológicamente, la palabra española matemático significa el que tiene gusto por aprender, estudioso, el que se dedica fuertemente a la ciencia o a algún trabajo intelectual, aficionado al aprendizaje."
que podemos abreviar como: "Amante del conocimiento". Y esa pasión por el saber también la transmitía a su alumnado por el que, en todos sus escritos, en sus desarrollos de recursos educativos y en todas sus actuaciones docentes, manifestaba continuamente no sólo preocupación, sino principalmente ocupación al perseguir la preparación y disposición de recursos que contribuyeran al óptimo aprendizaje de los discentes presenciales de su aula y a los discentes virtuales que gracias a las tecnologías actuales pudo llegar a enseñar sin llegar a conocerlos, todos ellos le tendrán agradecidos en su corazón, pues todos para crecer y avanzar necesitamos subirnos a "hombros de gigantes", como gigante él lo fue. Nosotros, tus colegas, añorándote sin poder colmar el duelo, también agradecemos que nos permitieras apoyarnos en ti y el haber podido contar con tus enseñanzas y ayuda, para juntos construir y mejorar la educación y nuestra sociedad.
En el primer capítulo de este libro, "Semblanza", podrán encontrar algunas pinceladas ildefonsinianas de quienes le hemos conocido y
tratado y, sobre ellas, ustedes, con sus propios pinceles construirán su retrato personal y profundizarán en el conocimiento de su persona y ser.
resolver, en ese contexto, dichos problemas de diversa formas y entre ellas usando como herramientas a las espirales.
Porque las espirales, esas curvas hipnóticas que llaman la atención de cualquier profano, fueron otro de los centros de interés y saber de Ildefonso. Y entre los antiguos: Hipócrates, Hipias, Dinostrato, Arquímedes, Nicómedes, Diocles, Eratóstenes; y los nuevos: Dure-ro, Descartes, Bernoulli, Pascal, Cotes, Varignon, Cornu, Mac-laurin, etc. se sintió bien acogido y docto.
Y casual o, quizás más bien causalmente —nuestro ser, a la vez que avanza como brazo de una espiral, también actúa como el polo de la misma y nos atrae conduciéndonos a la raíz, al origen e intemporal esencia familiar, la densa herencia genética que actúa cual agujero negro— en sus últimos años, ya jubilado, topó con la proporción cordobesaEl trabajo de divulgación "Las matemáticas en la belleza y la belleza de las matemáticas" fue el punto de contacto con esta proporción cordobesa, que fue nombrada así por el arquitecto Rafael de la Hoz Arderius, y que también la denominó como proporción humana al confrontarla con la proporción divina (áurea). que resonó en sus genes y tintineó en sus neuronas. Y la sipnasis de estas ignotas células que son alentadas y agitadas por las esquivas musas, junto al trabajo colaborativo con otros colegas al que siempre estaba predispuesto y dispuesto, le llevó a plantear cómo sería la espiral que habría dibujado Durero si en lugar de apoyarse en el crecimiento gnomónico de un rectángulo áureo y en su cuadrado gnomon para dibujar un cuadrante de circunferencia, hubiera considerado el crecimiento gnomónico de un rectángulo cordobés y, sin la impuesta limitación clásica de la regla
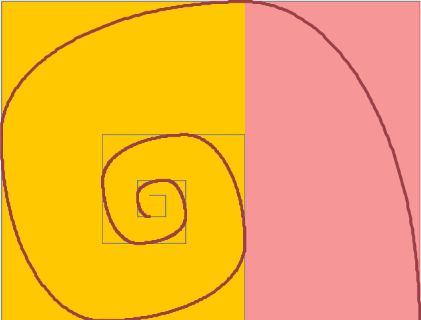
y compás, dibujara otras curvas en esos concatenados gnómones rectangulares. La espiral gnomó-nica cordobesa o espiral cordobe-sa de Durero tomó forma al considerar el dibujo de un cua-drante de elipse en cada gnomon y, con élla, la infinidad de espirales gnomónicas o espirales generali-zadas de Durero al considerar rectángulos con cualquier otra proporción. Tu satisfacción, nuestra complacencia, al visualizarla fue inmensa, pues la concreción de la inspiración que Martin Gardner denominó ¡Ajá! y la euforia arquimediana —¡Eureka!— que en ese momento se produce es bien conocida por quienes se han encontrado en alguna análoga situación. ¡Habrá que seguir escribiendo sobre estas espirales! ¿verdad, Ildefonso?, nos pasamos la vida recitando el ¡no tengo tiempo, no tengo tiempo! que Galois escribió en su última noche y en ello se nos pasa el tiempo. Las espirales generalizadas de Fibonacci quedaron también esbozadas... ¡Tendremos que retomarlas! ¿te parece, compañero?
Pero, es que en nuestro camino se cruzó un antiquísimo animalito, tanto que le llaman fósil viviente. Bueno, realmente lo que se interpuso fue su rastro vital, su bitácora cálcarea, su concha cuya forma ha atraído a todo el que observa a la Naturaleza y se pregunta sobre ella y, cómo no, es de especial atracción para los matemáticos porque su perfil tiene la forma y crece según una espiral. ¡Sí! ¿Cómo no vas a saber de qué hablo? Morfeo os ha abrazado juntos y aunque él es oriundo de lejanas tierras, del Indo-Pacífico, y tú fuiste turolense, ambos sois en esencia, en germen, paisanos, ¡sois cordobeses! ¡Qué subida de adrenalina! ¡Qué levitar! al descubrir que tu querido Nautilus, tanto tiempo encajonado en una proporción áurea que forzaba su frágil estructura calcárea, realmente para encuadrarlo, para
empaquetarlo adecuadamente necesitaba de un rectángulo más rechoncho, de ¡un rectángulo cordobés! Tu Nautilus era cordobéEn Córdoba (España) la pronunciación de las eses a final de palabra suele ser muy débil y para los oídos no habituados a esa tonalidad, éstas quedan como omitidas. La espiral que seguía, que sigue, el perfil de su concha era una espiral logarítmica cordobesa, el sifúnculo y los septos todos son arcos de espirales logarítmicas cordobesas.
¡Descansa en paz, compañero! Ya has superado la yocto-yotta realidad y Caronte te ha llevado al continuo matemático que tanto has estudiado, conocías bien cómo era y ahora, con seguridad, estarás feliz en él. Las limitaciones físicas que coartan el saber han caído, eras amante del conocimiento y ahora eres conocimiento puro.
¡Hasta siempre, amigo!
En este libro hemos recopilado tu producción durante los años que hemos compartido en RED Descartes. Los hemos organizado en varios
capítulos agrupándolos según los subproyectos de nuestra red: GEOgráfica, Evaluación formativa, Formación en competencias y Miscelaneas. Todos esos recursos, aunque los gestionamos y están en nuestro servidor proyectodescartes.org, los hemos ubicado en local para que formen un todo con el libro y no se vean afectados por la volatidad de la web y para que quienes lo deseen puedan volcarlos en un soporte personal y atesorarlo. También hemos incluido, localmente, los recursos de otros colegas que adaptaste a DescartesJS. Y, por supuesto, no hemos olvidado tus construcciones en GeoGebra que igualmente hemos descargado para que se vean localmente, pues esa web es ajena a nuestro proyecto y podría dejar de estar accesible o cambiar su direccionamiento. Y también tu web personal, alojada en el Ministerio, y a la que hemos aplicado igual criterio que en el caso anterior. Los artículos que publicaste en nuestro blog de RED Descartes han quedado descritos y enlazados, no te preocupes que cuidaremos que estén accesibles, si bien hay enlaces externos que no hemos podido recuperar, pues así es la web, una fuente de conocimiento voluble, donde se pierde fácilmente el conocimiento.
Con este libro queremos preservar la parte de tu saber y buen hacer que compartiste con nosotros y que divulgaste altruistamente durante tus años de colaborador del proyecto Descartes y socio de RED Descartes. En él volcamos todo nuestro cariño para ti y toda tu familia.
Desafortunadamente sólo nos queda tratar de mitigar el llanto con el que iniciamos este prefacio manteniendo tu recuerdo vivo y tratar de convivir con nuestra pena.
¡Te añoramos!
Los socios de la "Red Educativa Digital Descartes"
Imagen de portada del capítulo: foto de Ildefonso convertida en una pintura al óleo.
Imagen de esta página: Madrid Alex Azabache.
Ildefonso, en el contexto de un curso de formación, publica en un blog personal un artículo con el título Reflexiones, en el cual describe su Entorno Personal de Aprendizaje (Personal Learning Environment PLE). Lo transcribimos a continuación porque estimamos que de su lectura se pueden colegir algunos aspectos de su pensamiento, caracter y forma de ser:
Reflexión sobre mi red personal de aprendizaje
De ninguna manera pude prever el efecto clarificador que la realización de un esquema sobre mi Entorno Personal de Aprendizaje (Personal Learning Environment PLE) iba a tener sobre la percepción del camino seguido para obtener el bagaje que poseo y el camino a seguir para adquirir nuevos conocimientos, la realización de la tarea ha convertido procesos intuitivos, con una carga de incertidumbre importante, en procesos racionales perfectamente esquematizados, esto a pesar de las notables carencias que día a día descubro en el esquema PLE inicial y es que a veces los árboles no dejan ver el bosque.
Quizás la ausencia más notable en mi PLE inicial es la de los CAP (Centros de Apoyo al Profesorado), que si bien se han visto diezmados en su concepción inicial, los que quedan funcionan a pleno rendimiento (corregidme si no es así) y la ausencia del resto ha sido suplida satisfac-toriamente por el INTEF y otros organismos tal y como podemos observar en el gráfico siguiente:
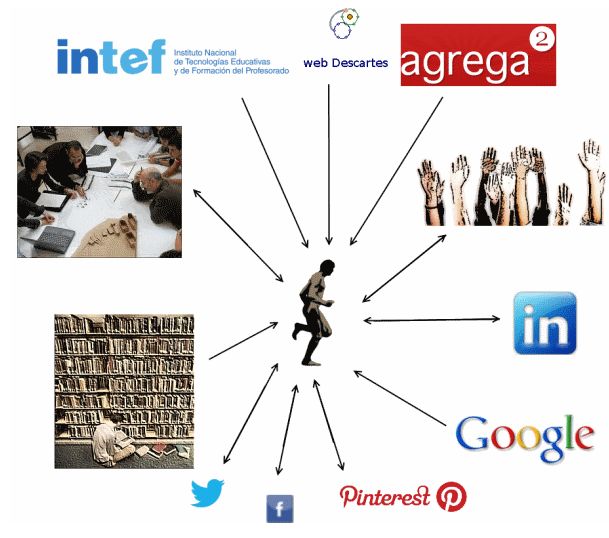
Por mi edad, puedo afirmar que gracias a los cursos realizados en los CAP, he mantenido un proceso de reciclaje continuo, en sintonía con las tendencias educativas del momento. En mi memoria guardo un grato recuerdo de los responsables de los diferentes CAP en los que he realizado cursos y de los responsables de dichos cursos.
Cierto que hay una notable diferencia entre los cursos presenciales, hasta no hace mucho todos lo eran, y los cursos a distancia como lo son la mayoría en la actualidad. Algunos compañer@s manifiestan la nostalgia
organizando “quedadas en la vida real” lo que me parece muy acertado, pues aunque el nivel, cantidad y calidad de los conocimientos que se adquieren en los cursos a distancia, técnicamente no ha disminuido, la capacidad y riqueza de la transmisión de conocimiento directa entre personas de un nivel intelectual similar y con unos intereses parecidos, reunidos por una temática concreta, es muy superior, según mi experiencia propia, y salvo excepciones, la satisfacción personal, también. Por lo que si se me diera la oportunidad de proponer algo propondría que los cursos fueran híbridos en una proporción de 6/4.
Desde siempre, en mi vida profesional, he tenido en mente que mi comunidad es la Comunidad Educativa y también que mis principales fuentes de información han sido mis compañer@s con quienes he interactuado muy satisfactoriamente aunque tengo tendencia a pensar que es mucho más lo que he recibido que lo que he aportado, cosa que por otra parte es normal, pues soy uno a dar y recibo de muchos. En la actualidad puede ser que cuando te preguntan ¿a qué comunidades perteneces? Te estén preguntando por las comunidades a las que estás suscrito en Internet o por las comunidades virtuales con las que interactúas. En este sentido las comunidades que me siguen aportando la posibilidad de reciclarme y de avanzar en el conocimiento son: EducaMadrid, INTEF, Proyecto Descartes, Proyecto Agrega y diferentes foros temáticos sobre Matemáticas en general, Geometría, Álgebra, Electrónica, Microelectrónica, programación, Mecánica y otros. En todas ellas, a excepción del espacio moodle que Educa Madrid ha asignado al IES Humanes, donde he sido usuario y administrador, soy usuario y para comunicarme con el resto de usuarios uso las herramientas que brinda la plataforma y en muy raras ocasiones la comunicación ha transcendido el entorno de la plataforma.
En cuanto a qué herramientas uso para conseguir reciclarme debo decir que además de la lectura de libros, la realización de cursos y la suscripción a revistas y organismos, uso el ordenador y, por lo tanto, Internet. Dentro de Internet uso Facebook, Twitter, Pinterest, LinkedIn y ocasionalmente otras.
Ahora bien, para mí, la mejor es Google, que no deja de encontrar lo que busco y de evolucionar aportando servicios adicionales de indudable valor.
Desde siempre, en mi vida profesional, he tenido en mente que mi comunidad es la Comunidad Educativa y también que mis principales fuentes de información han sido mis compañer@s con quienes he interactuado muy satisfactoriamente
El proyecto Descartes ha sido siempre un proyecto colaborativo de profesorado preocupado por su enseñanza, y también de su aprendizaje, interesado en trasladar su experiencia de aula en recursos educativos interactivos que ayuden a aprender a aprender y poniéndolos a disposición de la comunidad educativa, de manera altruista, en servidores de Internet para poder llegar a cualquier interesado en adquirir conocimiento. Tanto en el periodo en el que el proyecto estuvo patrocinado por el Ministerio de Educación español (1998 a 2012) como el periodo posterior como ong (a partir de 2013), los cursos de formación han sido la fuente principal de incorporación de nuevos miembros y socios.
Ildefonso realizó el curso de formación "Descartes 2" En ese momento se impartía el curso "Descartes básico" y "Descartes 2". El primero enseñaba los recursos de la web del proyecto, cómo localizar los contenidos deseados y un primer contacto con la herramienta de autor "Descartes". El segundo servía para el aprendizaje de la herramienta en sí, la elaboración de un recurso educativo con ella y una breve experimentación en el aula con ese recurso. El curso "Descartes 2" podía realizarse sin necesidad del haber hecho el básico. desde octubre de 2007 a enero del 2008". En él desarrolló un recurso educativo interactivo sobre el Teorema de Morley (ver el El recurso fue editado usando Descartes en su versión Java y posteriormente Ildefonso lo convirtió a DescartesJS, la fecha que figura actualmente al pie de la portada de este recurso es la de conversión. ). Él, nos indicaba que "El interés didáctico de este teorema es evidente ya que en su estudio y demostración se utilizan la mayor parte de los contenidos curriculares de los temas de Trigonometría, ecuación de la recta, distancias en el plano, resolución de sistemas de ecuaciones y otros" e indicaba en el apartado de enlaces de interés: "En la elaboración de este trabajo me han sido de gran ayuda..."
¡Siempre agradecido con los compañeros por el aprendizaje recibido!
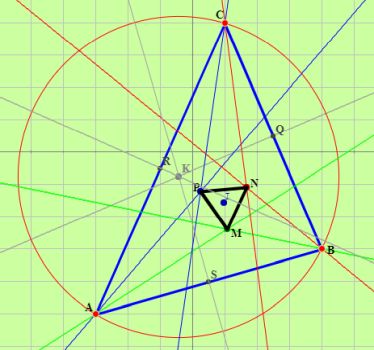
¡Haz clic sobre la imagen!
Su tutor en este curso fue nuestro socio Alfredo Pena Iglesias y él, con muy gran acierto, trasladó al coordinador del proyecto Descartes el interés y tesón que había mostrado Ildenso en el curso, así como el buen trabajo realizado y, por ello, recomendó que se le invitara a participar en nuestro proyecto.
Esa invitación se le cursó en junio de 2008, en el décimo cumpleaños de la herramienta Descartes y del proyecto Descartes.
Podemos acudir a la correspondencia electrónica mantenida con él y extraer algunos párrafos con el objetivo de conocer, a través de lo que escribía y cómo lo expresaba, un poquito cómo era Ildefonso.
21 de junio 2008
Para mí, ha sido un honor recibir tu invitación para participar en el proyecto Descartes, así que acepto gustoso.
Me ha gustado mucho el proyecto EDA Nota de los editores: Hemos enlazado la web de este proyecto de "Experimentación DidácTICa en el Aula" (inicialmente se denominó "Experimentación con Descartes en Andalucía", después "Experimentación con Descartes en el Aula" al ampliar la extensión geografica de la experimentación y finalmente el nombre antes citado al ampliar los ámbitos de conocimiento experimentados, siempre manteniendo el mismo acrónimo EDA). Puede que la introducción que citaba Ildefonso no fuera exactamente la que figura ahí ahora, pero en esencia trataría de la utilización de recursos TIC en el aula y de la necesaria planificación didáctica para su adecuado uso. , parecería que la introducción la había escrito yo, pues tal es mi experiencia personal. En cuanto proceda aportaré mi grano de arena.
Actualmente estoy trabajando, entre otras cosas en la Geometría clásica: Arquímedes, Pappus, Ptolomeo,…, con los programas: Geogebra, Cabri y otros y como bien sabes, pasar estos trabajos al nippe Descartes es casi inmediato, así que si ves alguna posibilidad por ese camino me lo dices y concretamos. Los aspectos curriculares que se repiten al trabajar con estos clásicos, son los de ángulos en la circunferencia, semejanza, Teoremas de Thales y Pitágoras etc.
Desde el primer correo Ildefonso manifiesta su interés en el uso didáctico de las TIC y de los recursos educativos centrándose en la práctica de Aula que no le es desconocida al incidir sobre su experiencia en ella.
También propone trasladar sus trabajos en GeoGebra a Descartes. Y siempre pensando en la enseñanza al citar los aspectos curriculares de los objetos interactivos que ha realizado y/o busca realizar.
22 de junio 2008
Ojalá pueda aportar algo. Así devolveré parte de las satisfacciones que el proyecto me ha procurado.
Las experiencias más satisfactorias que he tenido con el programa Descartes han sido con el uso de los trabajos de estadística y probabilidad que están en la miscelánea (carreras de coches y lanzamiento de dados) y con los temas de geometría relativos a los poliedros, desarrollos, áreas,… , eso desde el punto de vista del trabajo con los alumnos. Desde el punto de vista personal la lista es interminable y cada vez me satisface más que Google me envíe a una página del proyecto, lo que cada vez es más frecuente
En esta página: http://alerce.pntic.mec.es/~iferna14/ Está es su página personal en el servidor del Ministerio y está accesible y operativa a 8 de agosto de 2023. , puedes ver que, por operatividad, he situado el trabajo que hice para el curso Descartes.
Nos facilitó su página para ver lo que él tenía desarrollado y lo que podía servir de referencia para desarrollos a realizar con Descartes.
26 de junio 2008
Me preguntas sobre que me aporta Descartes frente a Geogebra, Cabri, Recta y Compás y otros. Pues que en Descartes ya están las unidades elaboradas, que esas unidades las han llevado a cabo profesores en activo con mis mismos problemas e idénticas necesidades de comunicación de conceptos, esto desde el punto de vista de uso de los materiales, desde el punto de vista de creación de los contenidos vuelve a ocurrir lo mismo, es evidente que el applet está creado por profesionales de la enseñanza y que su objetivo principal es el de servir para crear contenidos didácticos y aunque en esto último coincide con todos los demás programas, para mi, Descartes, tiene la cercanía de haberlo visto nacer, crecer y perfeccionarse y que al uso del programa me unen experiencias didácticas inenarrables por increíblemente satisfactorias, algo similar me ocurre con CLIC (y JCLIC), programa que para el primer ciclo es extraordinario y con el que he elaborado multitud de contenidos, gracias entre otras, a las ayudas de la web Averroes. Por otro lado, GeoGebra es tremendamente versátil y manipulativo y es muy adecuado para lanzarse en el camino de la creación y manipulación de objetos matemáticos.
Sobre las alternativas a la aspereza inicial de Descartes, ya las tenemos, afortunadamente, dentro del propio proyecto, creo que no es necesario que te mencione los nombres de los compañeros y compañeras que le dan a la presentación de sus unidades una apariencia, que cuesta hacerse a la idea de que estas proceden del mismo applet con el que uno mismo ha elaborado su unidad. Claro, no todos tenemos esa sensibilidad artística. Entonces quizás la alternativa pueda concretarse en ofrecer ciertas ayudas para las configuraciones estéticas de las escenas. En la práctica creo que el asunto no es trivial, ni mucho menos.
Nos detalla por qué le gusta Descartes y traslada que ha sido usuario del proyecto desde su nacimiento y reafirma su uso y el de otras herramientas en el aula. Comenta sobre las mismas destacando sus cualidades sin denigrar a ninguna de ellas. Traslada de manera sencilla y humilde, de manera natural, un conocimiento teórico y práctico que es extenso y profundo.
Disculpa que te reitere que estoy sinceramente entusiasmado en comenzar mis colaboraciones con el grupo
Respecto al proyecto PISA ¿qué decirte? He trabajado en este proyecto con auténtico entusiasmo dirigido por la catedrática de Álgebra de la Universidad Complutense Inés María Gómez Chacón, en unos cursos que hizo hace ya algún tiempo. Le hice un trabajo en el que usaba Flash. He visto algo de lo que habéis hecho y a falta de un análisis más detallado me ha gustado mucho.
En la fase inicial de ubicar los posibles trabajos con los que comenzara a contribuir a Descartes se le propuso usar preguntas liberadas de PISA para desarrollar recursos interactivos que se encuadraran en la evaluación formativa y, de nuevo, nos descubre, con agradecimiento a otra persona (siempre agradeciendo lo recibido por los demás), tener conocimiento sobre el tema y valorando positivamente el material que se le aportó como referencia, el cual estaba desarrollado con Descartes.
1 de agosto 2008...además de maravillado (sistema planetario) sorprendido (corrección sumativa de los ejercicios, series de ejercicios…) entusiasmado (modularización) y no se que otros adjetivos emplear pues según avanzo descubro que en los nuevos trabajos casi todo es novedoso para mi y más aprecio la increíble labor que estáis desarrollando hasta tal punto que la puesta al día se me hace imprescindible y que por lo tanto, ahora, me siento algo desbordado, además, en este sentido, me sería de gran utilidad poder disponer de la documentación sin conexión de la versión 3 de Descartes… bueno, tampoco me agobio demasiado, estamos yendo y quien va piano va lontano, dicen.
Si a la propuesta de centrar mi actividad en la creación de material para el aspecto sumativo y formativo (ASIPISA), si porque ya llueve sobre mojado en el tema, que ha sido objeto de debate, en un seminario que hemos hecho este mismo curso pasado, así pues, en cuanto tenga las instrucciones y la formación necesarias me pongo con la tarea.
...ahora estoy con las espirales que me ha resultado ser un tema muy rico en posibilidades aunque no para el currículo actual.
Te reitero que para mi tu llamada para invitarme a trabajar en vuestro grupo ha supuesto un aliciente adicional para aprovechar estas vacaciones, gracias, también gracias por tu gentileza y paciencia.
En espera de recibir tus gratas noticias, me despido de ti.
Al adentrarse en el material aportado como guía, descubre interioridades sobre la estructura interna del código que se utiliza en él, el cual va encaminado a facilitar el desarrollo de recursos encuadrados en un mismo subproyecto. A la vez de realizar una valoración positiva, como ya sabemos que era habitual en él, se ve algo desbordado, pero automáticamente pone el remedio al marcar la necesidad de ampliar su estudio de la documentación de la nueva versión de Descartes, la tercera, y pide su acceso a ella de forma local (nos comentó que en su lugar de vacaciones la conexión que disponía era en una biblioteca pública y también recordemos que en 2008 las velocidades de conexión a internet distaban bastante de las actuales).
También era habitual en él acudir a citas coloquiales, aquí escribe: "quien va piano va lontano".
Acepta trabajar en recursos sobre PISA desde el punto de vista no sólo evaluador o sumativo, sino formativo.
Y surge un tema que le apasionaba: ¡Las espirales!. Tema que como ya hemos indicado era una pasión y en el que nos adentró en el transcurso de los años.
5 de octubre de 2008
Solicité el curso de tutor porque me parece la mejor manera de recordar los contenidos y actualizarme, ojalá me encuentre una plaza.
Se refiere al curso de tutor a distancia de los cursos del CNICE. Siempre buscando formación...
19 de octubre de 2008
…acepto todas tus sugerencias y los cinco ejercicios voy a tratar de que sean tres…
Lola me ha apuntado para el curso de tutores en Enero, me ha dado una alegría.
Muestra su apertura a cualquier ayuda y sugerencia, se adapta a las necesidades y requisitos de un proyecto y colabora en la consecución de objetivos. Fue admitido en el curso de tutores a distancia que tanto interés tenía en cursar.
22 de noviembre de 2008
...entre los estrógenos, cocos, virus y demás bio-vocablos y los avatares propios de nuestra-materia-propia ando justo de energía y tiempo, pero mantengo intacta la ilusión de llevar a buen puerto nuestro proyecto y más ahora que, creo, hemos superado las dificultades iniciales.
Preocupado por lograr cuanto antes llegar a una producción de recursos y conseguir los objetivos que se le han ido indicando y salvadas las dificultades iniciales de profundización en su formación en Descartes transmite que está realizando la tarea acordada y con ilusión intacta. Reseñemos aquí que los colaboradores de Descartes somos profesores y que esta tarea adicional ha de realizarse en nuestro tiempo libre, por tanto la producción está condicionada a múltiples avatares laborales, familiares y personales. Los tiempos han de medirse de manera diferente.
13 de enero de 2009
Adjunto te envío la primera unidad con tres problemas. Puedo añadir, modificar o suprimir cualquier cosa, espero tu respuesta para hacerlo o para comenzar con otras, por ejemplo una dedicada a las progresiones Aritméticas y otra a las Geométricas con 3, 4 ó 5 ejercicios cada una, si te parece bien.
Logra completar su primera unidad de evaluación formativa. Nótese, por la fecha, que parte de las vacaciones de Navidad han servido para cerrar la entrega de este recurso. Se manifiesta atento a cualquier indicación que se le dé y apunta, una vez habituado al esquema y al código interno común que tienen los objetos de este proyecto, a iniciar otros dos recursos.
15 de febrero de 2009
Gracias por tu ofrecimiento, intentaré estar al tanto del foro y en cuanto vea la oportunidad colaboraré con mis aportaciones. Por ahora me enriquezco con las vuestras, por lo que os estoy agradecido, pero aún no tengo el nivel adecuado para entrar como actor.
Se refiere al foro privado de los colaboradores del proyecto en el que se la ha pedido presente sus ideas, opiniones y desarrollos, y aunque no rechaza participar pronto, su modestia le hace ver más interesante lo ajeno que lo propio y considera que su nivel es inferior a lo que en ese foro se está expresando, lo cual era algo más bien relativo.
13 de abril de 2009
Gracias por vuestro amable recibimiento en el foro, el tuyo y el de Navarro, estoy deseando saludaros personalmente. Parece que algún compañero empieza a valorar la dinámica de la evaluación formativa y estoy viendo, en el foro, participaciones que lo atestiguan, creo que el trabajo colaborativo es más productivo.
He finalizado el curso de Tutor e Internet y me ha gustado mucho, he tenido de tutor a Juan José Bermejo que me ha ayudado muy eficazmente.
Sin saber muy bien como he iniciado relaciones con personas responsables en la creación y uso de software libre para el área de Matemáticas y en particular de matemática dinámica, de universidades Argentinas y Españolas y con un proyecto de ayudas a la colaboración entre universidades de ambos lados del océano.
…posibilidad de integrar Descartes y Geogebra...
Finalmente interviene en el foro del grupo Descartes presentando su trabajo y manifiesta, de nuevo, gratitud por los comentarios recibidos.
Lo habitual entre nosotros es el trabajo a distancia y el conocimiento en persona se da en las reuniones anuales que solemos tener si puedes asistir. Pueden transcurrir muchos años de colaboración y trabajo conjunto y no conocernos presencialmente, pero ello no es óbice para establecer relaciones estrechas y amistades. Obviamente el tener alguna sesión de trabajo presencial y compartir mesa y mantel sirve para incrementar la cohesión grupal y personal.
Nos comenta las relaciones que ha establecido con otros grupos de trabajo en el ámbito de la herramienta GeoGebra. E incluye el deseo de integrar Descartes y Geogebra. Esta integración, o mejor dicho comunicación entre ambas herramientas, requirió una previa
comunicación entre las escenas de Descartes y el contenedor html que le da soporte, pero se logró en el desarrollo de la versión DescartesJS En el libro interactivo "Comunicación DescartesJs-GeoGebra (2.ª edición) se tiene una completa descripción del proceso y se cubren las diferentes necesidades que puedan surgir a los interesados en este tema. .
3 de mayo de 2009
Acumulo retardos porque me embarco en todo lo que me ofrecen y no escarmiento, año tras año, a pesar de los propósitos de enmienda. Ahora acabo de terminar un extraordinario curso de Historia de las Matemáticas a cargo de Mariano Martínez y José Manuel Rey, ambos de la Universidad Complutense.
Publicaré en el foro el enlace actualizado al proyecto Pisa y en cuanto consiga terminar los polinomios y funciones te los enviaré.
...no te he concretado más porque en realidad todo está un poco en el aire y no quiero aburrirte con pormenores que quizás luego sean otra cosa.
Una constante que se repite en los cartesianos y también en Ildefonso, la inmensa necesidad de ampliar el conocimiento que conduce a diversificar los focos de interés y que, a veces, conlleva inquietud y desasosiego al producirse ciertos retrasos en lo comprometido, sin que llegue a ser un incumplimiento.
31 de mayo de 2009
He estado creando unas páginas para mis alumnos de 3º de la ESO relativas a las cónicas y basándome en los trabajos de José Ireno sobre el Globo terráqueo, que he usado con los alumnos de diversificación, he pensado en el siguiente esquema:
— JavaScript, para dinamizar la interacción con el usuario y evaluación con formulario tipo test.
— Geogebra para la manipulación dinámica de los conceptos estudiados.
— ASIPISA para la consolidación y evaluación formativa de los conceptos
Sigo con satisfacción los avances del grupo y las aportaciones.
Desasosiego en días anteriores y nuevo proyecto en el que se embarca y que ejecuta y además planificando con diferentes herramientas según la necesidad didáctica planteada. Y satisfacción continua con los recursos aportados en el foro del grupo. Inquietud docente y personal continua.
Podríamos seguir, pero con lo reseñado en las páginas anteriores consideramos que hemos cubierto el objetivo de conocer un poco a Ildefonso a partir de sus correos.
Y hemos llegado a un momento difícil porque somos conscientes de que nuestra visión sobre su persona es parcial, si bien podría decirse que así ocurre sobre cualquier persona en cualquier circunstancia y momento. Por ello, desde aquí, sólo trataremos de trasladar nuestra percepción de Ildefonso en determinados aspectos de su personalidad acordes al tipo de relación mantenida y a los medios sobre los que ella se ha construido.
Ya hemos indicado con anterioridad que nuestro trabajo cooperativo y colaborativo en el grupo Descartes se desarrolla a distancia y en muchos casos sólo habiéndo cruzado algunos correos en los que se establecen lazos e intereses comunes educativos o de aprendizaje personal o bien meramente con fines muy concretos como desarrollar unos determinados objetos dentro de un subproyecto y, a partir de ello, se inicia la colaboración para conseguir ese objetivo común. Por tanto, digamos que se construye una relación virtual en lo personal, una relación que conoce sobre objetivos concretos y temas particulares y que, en principio, ignora las circunstancias del entorno vital diario de cada cual, entorno que se desarrolla de manera independiente a cientos de kilómetros, incluso a miles. Y si bien son posibles las conexiones síncronas de voz e imágenes lo usual es utilizar herramientas asíncronas como el correo eléctrónico, o análogas como WhatsApp, porque la comunicación no se establece en base a una disponibilidad simultánea de los interlocutores que siempre está sujeta a más inconvenientes y dificultades al tener que cuadrar el tiempo libre, que es el dedicado a la RED Descartes, con el laboral y familiar.
No obstante, es bien posible establecer vínculos que trascienden los meros aspectos laborales (en este caso dígamos lúdicos porque se hace de manera altruista, por afición y motivación personal o grupal)
e ir conociendo a una persona, en base a relaciones epistolares. De hecho en la sección anterior hemos tratado de mostrarlo y usted habrá elaborado su visión personal. No es nada nuevo, pues así ha acontecido en épocas en las que las comunicaciones eran más lentas y difíciles, y así puede acontecer en este momento en el que son casi instántaneas.
Todo lo anterior no es óbice para usar el teléfono o la video- conferencia cuando se estima necesario bien para agilizar un proyecto o bien para facilitar la resolución de dudas que se harían más díficiles por otros medios y en esas comunicaciones se amplian las sensaciones y las percepciones.
Y lo mejor, poder realizar reuniones presenciales en las que se incrementan esas relaciones directas y profundizar en el conocimiento mutuo y fomentar la amistad.
Consecuentemente, los que tuvimos que tratar y trabajar junto a Ildefonso, estamos de acuerdo en ciertos aspectos de su personalidad.
De apariencia sosegada trasmitía confianza, seguridad y sobre todo humanidad.
Creativo, interesado en aprender, sabio y humilde. Confiable, ordenado y cumplidor con sus compro- misos. Amable, cordial, respetuoso y cooperativo.
Ante todo fue un gran compañero y una excelente persona.
Y a nuestras pinceladas impresionistas queremos añadir algunas que son mucho más firmes y seguras, procedentes de su familia, de su esposa Alicia Isabel y de sus cinco hijos: Diego, Homero, Antonio, Carlos y Adora. Las hemos podido recabar a raíz de la comunicación que nos hicieron de su fallecimiento. En ellas nos transmiten las sensaciones respecto a las vivencias experimentadas y compartidas por Ildefonso en relación al proyecto Descartes, y respecto a su vida familiar.
Su hija Adora, su pequeña, es quien estableció contacto con nosotros para transmitirnos tan triste noticia. Ella ha sido el nexo comunicador, la portavoz de la familia, por lo que hay que reseñar que en los mensajes aparece su nombre, pero siempre ha de entenderse procedente de todos los miembros de su familia. Nos insistió en ello y que explícitamente se especificara.
La noticia de su deceso nos llegó a través del WhatsApp personal de Ildefonso. Un mes antes le habíamos escrito invitándole a que acudiera a Córdoba, a la Asamblea anual de RED Descartes conmemorativa del 25.º aniversario del proyecto y no habíamos tenido respuesta. Nos extrañó, pero a veces las circunstancias familiares y personales hace que no se puedan antender las comunicaciones de nuestra asociación y tampoco se puede crear una presión o desasosiego a los socios que bastante hacen con prestar su tiempo libre y altruismo para el bien de nuestra comunidad, como ya hemos indicado anteriormente. Esperábamos que fuese una respuesta a la invitación indicando la causa del retraso o un simple comentario al artículo del blog sobre la Asamblea o sobre un nuevo artículo que hubiera escrito para el blog y fuera a publicar, o un mero saludo veraniego... pero, lo que leímos tuvo un inesperado y noqueador contenido.
Tarde del 28 de julio de 2023 (viernes)
Buenas tardes, soy Adoración, la hija de Ildefonso. Mi padre ha fallecido la noche del jueves después de unos meses luchando contra el cáncer. Creo que eres compañero del proyecto Descartes y quería comunicartelo. Si queréis podéis poner algo en la web del proyecto para ponerlo en conocimiento de la comunidad. Gracias por haberle brindado tanta ilusión con el proyecto.
Depués de haber podido terminar de leer el mensaje, dado que una vez alcanzada la segunda frase no pudimos continuar con el resto, nos parecía estar leyendo y oyendo al propio Ildefonso, no sólo porque procediera de su mensajería personal, sino porque rezumaba el mismo verbo y tono, y ¡cómo no! el reiterado y eterno agradecimiento propio de sus escritos, impregnado de satisfacción personal por parte de quien lo envía y de reconocimiento a quienes le han acompañado en el aprendizaje.
Y una vez que ya pudimos darle respuesta y comentarle brevemente algún trabajo de su padre...
Él os tenía gran estima. Me alegra mucho lo que me dices, gracias. Le habéis dado mucha felicidad. Aquí tiene algunos Nautilus en su despacho. Muchas gracias por el cariño.
Este año he empezado el grado de matemáticas, Dios quiera que consiga terminarlo y seguir el relevo de mi padre. Si publicáis algo en la web, por favor házmelo saber.
En un posterior mensaje le dimos conocimiento de la comunicación del fallecimiento a los socios de la RED Descartes y que Ildefonso estaba incluido en dos grupos de WhatsApp uno de RED Descartes España y otro de cartesianos iberoamericanos y que en ellos se estaban manifestando las condolencias, de las cuales le facilitamos copia, y que si lo estimaba oportuno podía acceder y responder a las mismas en esos grupos.
Adora, representando a toda su familia, escribió estos dos mensajes:
Grupo de WhatsApp iberoamericano, 2 de agosto de 2023
Estimados compañeros de mi padre, soy Adora, hija de Ildefonso.
Agradeceros a todos por las oraciones y mensajes de cariño y apoyo a mi padre y a nuestra familia.
Mi padre era una persona extraordinaria, es inevitable no echarle de menos pero nos queda el consuelo de que sigue vivo en nuestros corazones, en el recuerdo y en su legado y en que confío que sienta paz, gozo y amor en la gloria de Dios.
Pertenecer a ésta, vuestra comunidad, le proporcionó desafíos, compañía, ilusión y alegría, por lo que no puedo estar más agradecida con todos vosotros por haberle aportado felicidad a mi padre.
Un abrazo.
Grupo de WhatsApp RED Descartes España, 2 de agosto de 2023
Estimados compañeros de mi padre, soy Adora, hija de Ildefonso.
Me gustaría agradeceros a todos por los mensajes de condolencias y apoyo que habéis enviado con motivo del triste acontecimiento.
Agradeceros también por toda la felicidad que habéis reportado a mi padre al formar parte de vuestra comunidad. Mi padre era una persona extraordinaria que será amada eternamente y seguirá viva en nuestros corazones y en el gran legado que ha dejado. Dios lo tenga en su gloria y quiera que sienta paz, gozo y amor cada segundo de la eternidad.
Un abrazo.
De los contactos que mantuvimos para recabar y poder verificar alguna información sobre su formación académica y laboral con objeto de poder reflejarla con certeza en el artículo que estábamos elaborando en memoria de Ildefonso, y de la previa revisión que pedimos a su familia que hiciera de nuestro borrador podemos reflejar algunos comentarios y algunos datos no incluidos en dicho artículo:
Hola, muchísimas gracias por el artículo.
En la primera lectura que acabo de realizar me ha parecido emotivo y mejor que bien.
Voy a revisarlo detenidamente, aprovechando que he encontrado distintas titulaciones de mi padre, por si pudiera sugeriros algún retoque como me pides.
Tardaré un ratito ¿vale?
Y al día siguiente...
Buenos días, ya he respondido a tu petición vía email para mayor comodidad al ser un texto extenso.
A las menciones de sus trabajos con vosotros, comentarte que para él fue muy especial y significativo un proyecto que realizó sobre la espiral de la concha del Nautilus y su relación con la razón humana o cordobesa, por si os pareciera adecuado mencionarlo ya que nosotros lo vinculamos mucho con él, tanto que ha sido enterrado con un Nautilus. Se esmeró mucho en conseguir multitud de ejemplares que a día de hoy sigue teniendo en su despacho.
Ciertamente era imperdonable que se nos hubiera olvidado incluir la referencia al análisis de la concha del Nautilus...
En cuanto a la frase de agradecimiento del final del artículo a la comunidad de Descartes, aunque os la he trasladado yo, os pediría que pusierais que es de parte de su familia, ya que a mi madre y hermanos también les gustaría participar del agradecimiento a todos vosotros por todo bueno lo que le habéis proporcionado a mi padre.
Reiterando mi más sincero agradecimiento y esperando que no resulte una molestia toda esta información.
Realizadas las modificaciones a la redacción del artículo y solicitada una nueva revisión...
Muchas gracias por adaptar el artículo.
Por mi parte no puedo sugerir nada más a esta nueva versión que encuentro muy bien, y desde luego, lo mejor es el detalle. No obstante, se lo he reenviado a mi madre y hermanos para que den su opinión.
Mi padre me hablaba mucho de los libros interactivos y quería que yo aprendiera, a ver si algún día… por lo pronto estoy deseando que llegue el día para ver el que estáis preparando, para nosotros va a ser un gran regalo.
Gracias y un abrazo.
Mi madre y hermanos elogian vuestro artículo. Es espléndido y muy simpático el comentario del Nautilus, ¡que es cordobés! 😄
Y el gentilicio da pie a otros comentarios...
Jejeje, supongo que sabes que mi padre era un cordobés nacido en Teruel ¿no? Creo que por eso le entusiasmó tanto esa investigación.
¿Padres cordobeses?
Así es, de Montoro y Priego.
Mi abuelo era guardia civil y le destinaron a un pueblecito de Teruel, allí le mataron en acto de servicio y no pudo regresar a su tierra.
Mi abuela regresó con mi padre siendo un niño y ya luego marcharon a Madrid donde pasó mi padre el resto de su vida.
Después con la edad conveniente se fue a estudiar a Madrid en el Colegio Infanta María Teresa para huérfanos de la Guardia Civil donde una vez licenciado trabajó un tiempo como profesor.
Con la información contrastada con la familia, con nuestras vivencias compartidas con él y con sus colaboraciones en el proyecto Descartes elaboramos el artículo "Ildefonso Fernández Trujillo, in memoriam".
Y Adora, en representación de su familia, nos decía...
Gracias. No puedo dejar de leerlo. Qué bonito detalle. Sois muy buenas personas y muy buenos compañeros ❤️
¡Gracias a toda tu familia, Ildefonso! ❤️
Algunas personas jamás nos dejan…
¡están para siempre!
Imagen de portada del capítulo: Ildefonso y un puzle.
Imagen de esta página: árbol bajo el cielo estrellado, en Namibia (Harry Cunningham).
Los antecedentes de este proyecto se ubican en una aplicación que hace años desarrolló en Visual Basic el promotor de este proyecto (Ildefonso Fernández Trujillo) y que, posteriormente, procedió a adaptar en HTML. Al observar en la documentación de Descartes un ejemplo, desarrollado por el presidente de la Red Educativa Digital Descartes Colombia –el Dr. Juan Guillermo Rivera Berrío— en el que muestra una aplicación de los ficheros y vectores de Descartes para la identificación de las capitales europeas, renació la inquietud anterior. Ello ha dado lugar a una colección de unidades didácticas cuyos objetivos fundamentales son: el entrenamiento de la memoria, el desarrollo de la agudeza visual y la competencia lectora y obviamente facilitar el estudio del nombre de las capitales, de los ríos y formaciones montañosas de los países de los cinco continentes y de su situación geográfica en un mapa mudo. Una colección que nace como germen o base sobre la que seguir construyendo, buscando conformar un equipo de interesados en esta temática y área de conocimiento.
Los objetos publicados se agrupan en cuatro bloques:
En ellos se trata de conjugar el carácter académico o curricular y el aprendizaje mediante el uso actividades lúdicas (lo que actualmente se encuadra en la "gamificación" o aprendizaje a través del juego).
El bloque de GEOcolor plantea el aprendizaje e identificación de países y estados, cuenta con dos versiones.
Se trata de un puzle en el que al desplazar las piezas sobre un mapa base y al quedar posicionada cada una de ellas, se refleja su nombre. Es un objeto que ayuda aprender los nombres y memorizarlos.
Ildefonso participó, en 2016, con el mapa de África:
¡Haz clic sobre la imagen!
En la página siguiente, hemos ajustado la escena a formato vertical.
Se presenta un mapa base en el que se debe marcar la región sobre la que se pregunta (clic sobre el punto correspondiente). Al marcar la correcta ésta se colorea y muestra su nombre. Es un objeto que permite repasar y comprobar nuestro saber sobre África.
También, en 2016, Ildefonso participa con el diseño de la escena interactiva correspondiente al mapa de África.
¡Haz clic sobre la imagen!
En GEOcapital se presentan los diferentes países agrupados por continentes y se busca identificar sus capitales. Se cuenta con tres versiones para seleccionar la capital del país sobre el que se está preguntando.
En estos objetos interactivos se geolocalizan las capitales y se pide al usuario que ubique aquella sobre la que se pregunta. Si su respuesta es errónea se marca con un círculo cual es la ubicación correcta.
Las escenas diseñadas utilizan la API de geolocalización de Google Maps. RED Descartes tiene la autorización de Google para su uso, pero restringido a nuestro dominio proyectodescartes.org. Así pues, sólo funcionan on line y por ello omitimos la posibilidad de descargarlos ya que no funcionarán en local.
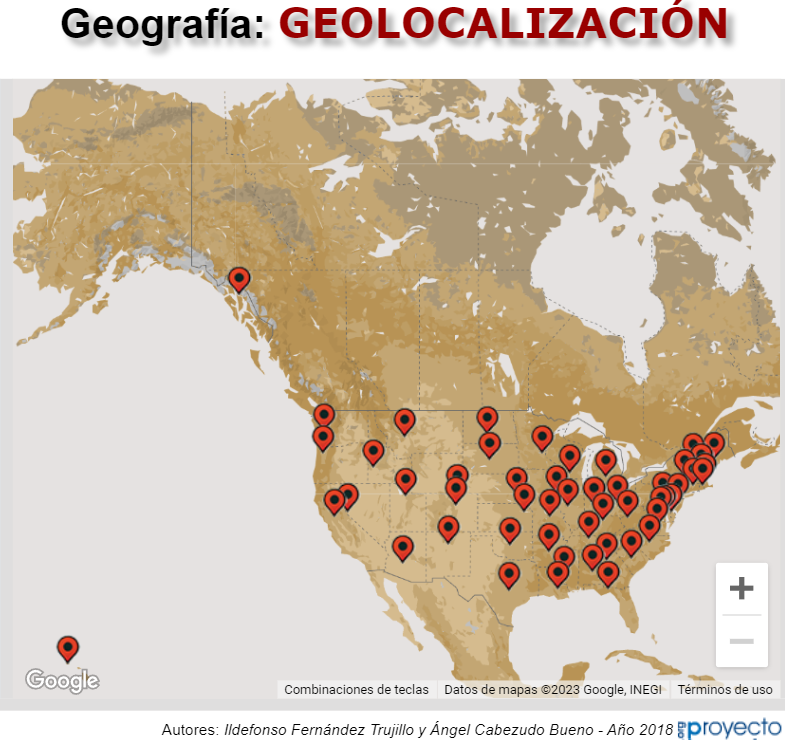
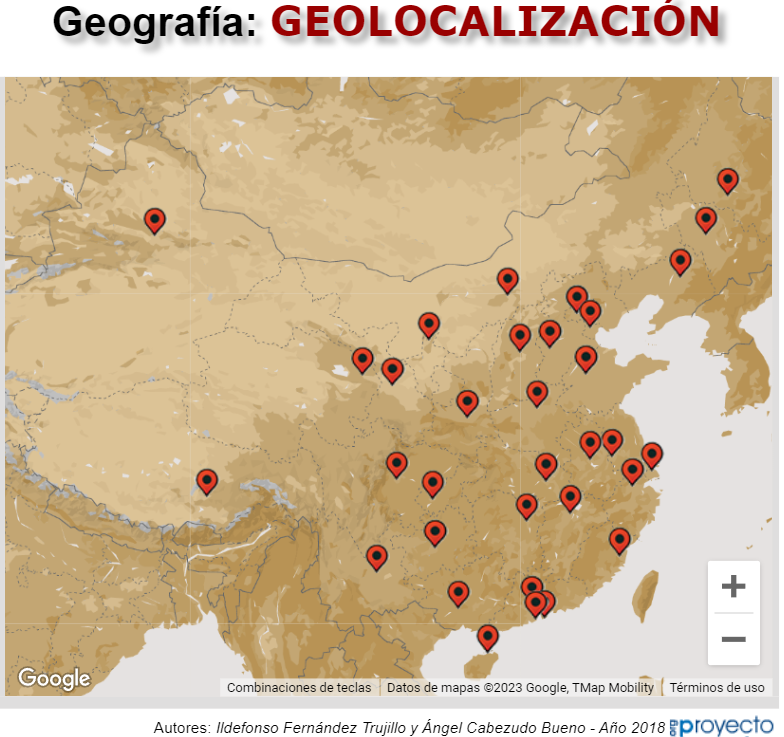
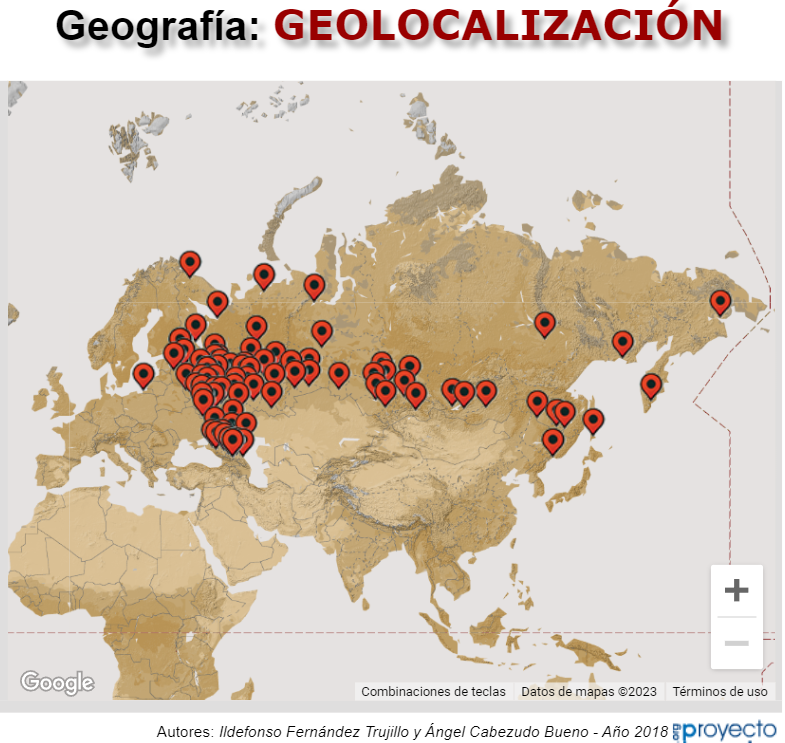
Ildefonso Fernández Trujillo y Ángel Cabezudo Bueno se unen, en 2018, para participar con cuatro escenas, que corresponden a:
|
|
|
|
Escena interactiva que mediante la elección de una opción dentro de las ofertadas en un menú desplegable, puede obtenerse la capital que corresponde a la pregunta.
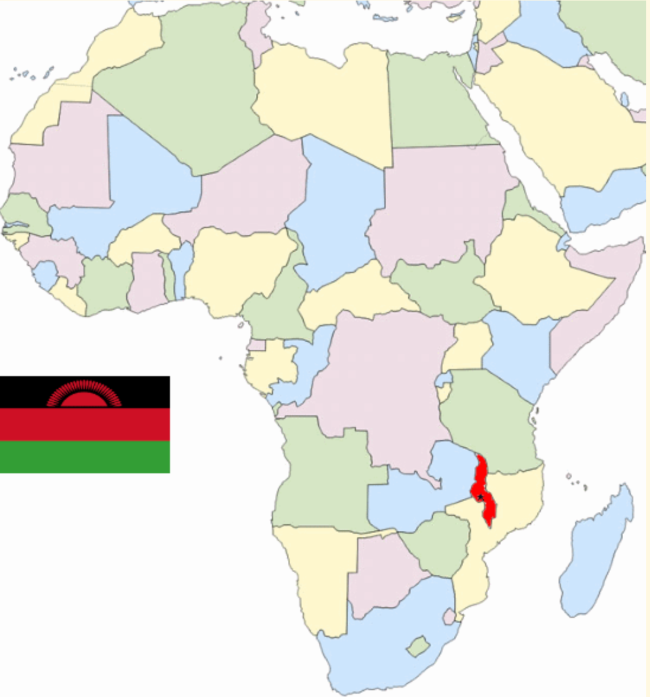
Las cinco escenas fueron diseñadas por Ildefonso en 2015, cuyo propósito es localizar, en una lista desplegable, la capital del país propuesto. La lista de capitales puede desordenarse para así facilitar a la vista una serie de ejercicios que redundarán en la adquisición de velocidad lectora. Haz clic sobre una de las siguientes imágenes o interactúa con la escena de la siguiente página:
|
|
|
|
Escena interactiva que mediante el posicionamiento con el ratón, o con el dedo en dispositivos táctiles, del punto que representa la capital, se obtiene la respuesta en un mapa clásico estático.
Las cinco escenas, cuyo propósito es localizar en un mapa mudo las capitales de los países, fueron diseñadas por Ildefonso en 2015. La interactividad hace que, después de un breve uso de la utilidad, mejoren los conocimientos del mapa político del continente y, por tanto, los resultados escolares. Haz clic sobre una de las siguientes imágenes o interactúa con la escena de la siguiente página:
|
|
|
|
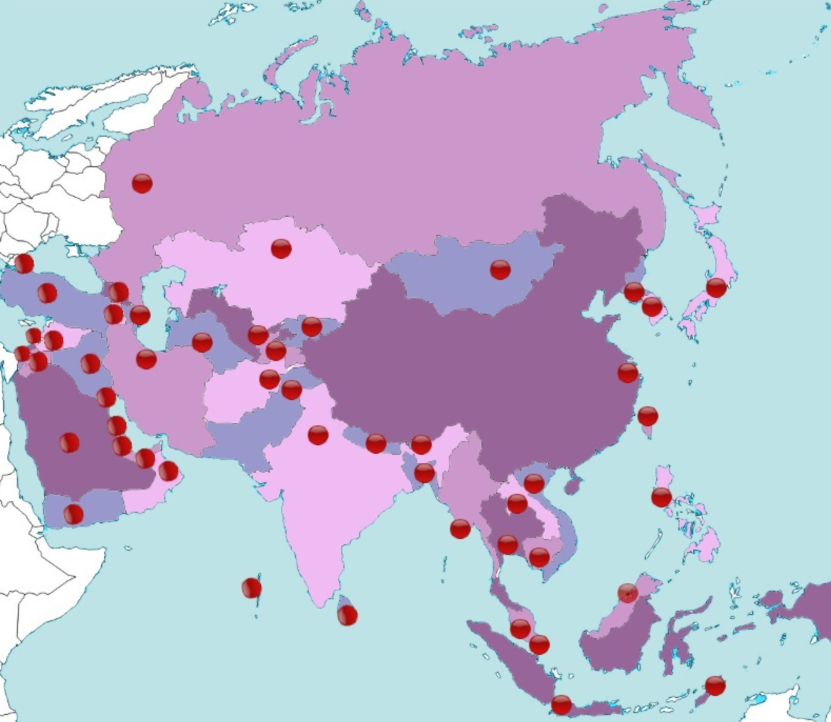
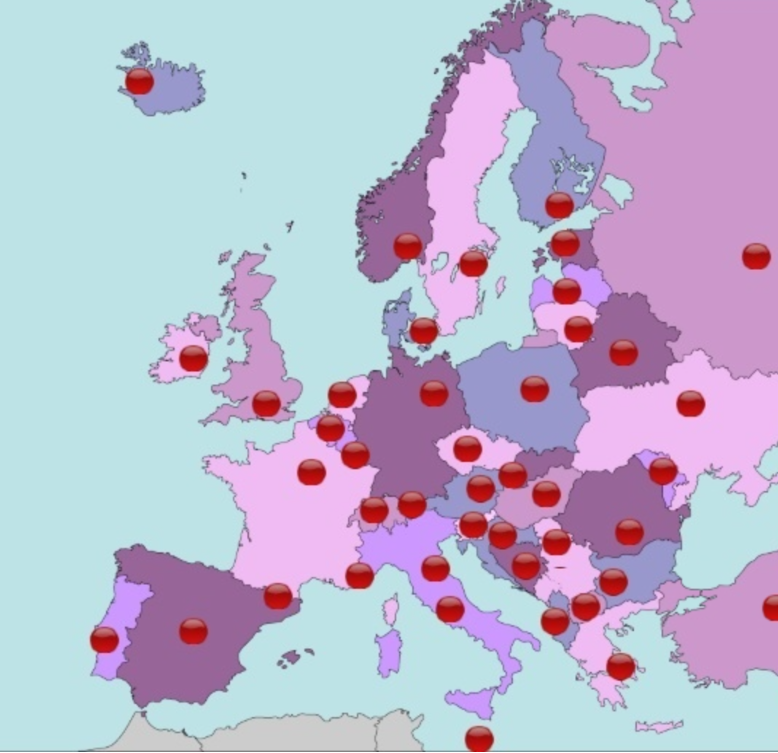
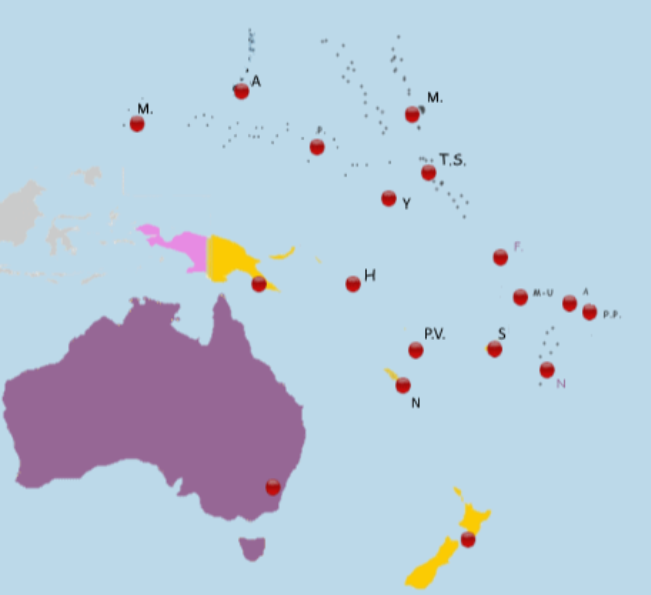
El bloque de GEOdiver se ha planteado como una biblioteca en la que cada libro agrupa un conjunto de actividades relacionadas con un tema, que es centro sobre el que se desarrolla la práctica y el aprendizaje.
La biblioteca GEOdiver contiene siete libros, diseñados con el segundo modelo de libros interactivos del proyecto iCartesiLibri. Cada libro contiene actividades lúdicas que pretenden, a través de la diversión y el entretenimiento, un acercamiento a los lugares geográficos de un continente o de algunos países
En cada libro se encuentran, entre otras actividades, puzles, sopas de letras, parejas escondidas y el juego del ahorcado.
El libro diseñado por Ildefonso corresponde al continenta africano, tal como se indica en la imagen animada de la página siguiente.
Haz clic en cualquiera de las imágenes, presentadas en estas dos páginas, para abrir el libro de Ildefonso
El libro de Ildefonso incluye las siguientes actividades: el juego del ahorcado, dos puzles de desplazamiento, un puzle memoriza, el juego de la "lupa cartesiana", dos puzles de intercambio de piezas, dos puzles giratorios y dos sopas de letras.
"Los niños y niñas no juegan para aprender, pero aprenden porque juegan"
Jean Piaget
En GEOevaluación los objetos son agrupaciones de actividades de diferente tipo: de selección, de agrupación, de clasificación, de asociación, de intercambio, de emparejamiento con textos e imágenes, con el objetivo de abordar un evaluación de conocimientos geográficos y culturales de forma amena y variada.
En este apartado del proyecto, se diseñaron seis GEOevaluaciones, tres de continentes (África, Suramérica y Asia) y tres de naciones (Estados Unidos, Francia y México). Ildefonso diseñó la GEOevaluación de África, a la cual puedes acceder haciendo clic en la siguiente imagen:
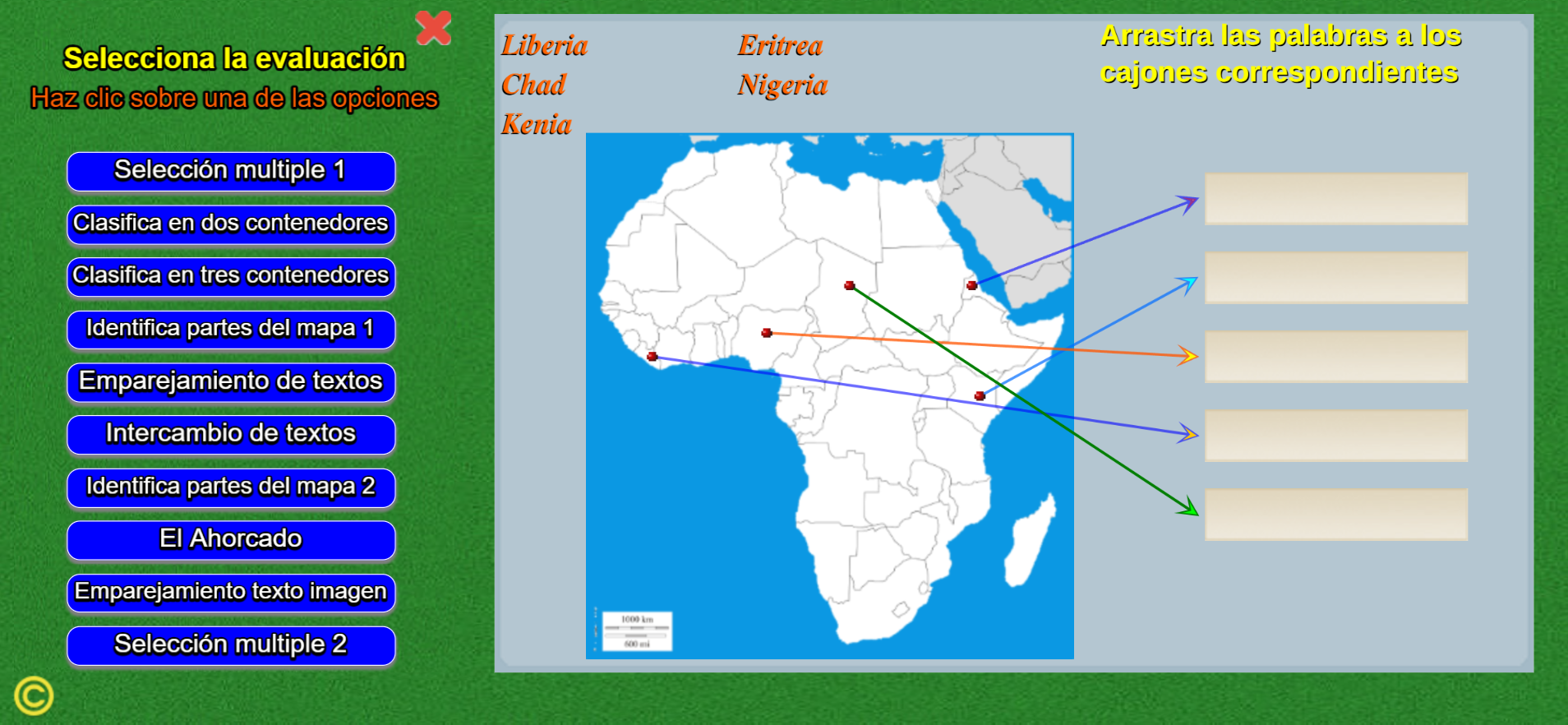
Ildefonso incluye 10 actividades evaluativas; entre ellas, el juego del ahorcado, que hemos adaptado al formato vertical, tal como se aprecia en la página siguiente ¡Haz clic sobre las letras, para que pruebes tus conocimientos sobre las capítales de las naciones africanas.
Imagen de portada del capítulo: Ildefonso y Proyecto Competencias.
Ermita de Nuestra Señora de los Santos en el pueblo de Móstoles, Madrid (Zarateman, CC BY-SA 4.0).
Las unidades PISA tienen como objetivo la realización de una evaluación sumativa, es decir, la obtención de una puntuación que permita la elaboración de los indicadores buscados en este Programa Internacional. Sin embargo la generación de números aleatorios permite introducir en una unidad PISA elementos que conducen a la posibilidad de realizar un tipo de ejercicio, pero de manera que, en cada instancia, muestre un aspecto diferente o presente datos distintos. Esta circunstancia hace que el discente pueda practicar con los conceptos inmersos en una unidad, posibilitando no sólo la evaluación sino también su aprendizaje. Recursos en los que se ha utilizado esta técnica los tenemos en el proyecto Competencias de RED Descartes en el que también participó Ildefonso.
En esta capítulo mostramos un conjunto de recursos en el que se aporta la posibilidad de realizar una evaluación formativa a partir de las unidades PISA, es decir, se busca la introducción de mecanismos que permitan de manera automática evaluar las respuestas que aporta el discente, pero no limitándose a aportar una corrección, sino acompañarla con orientaciones y una guía que permita el aprendizaje buscado. Guía que, incluso, puede producirse también aunque la respuesta aportada sea correcta, para verificar que ésta no ha sido elegida en un mero proceso de selección al azar.
También se enlaza con documentación complementaria que nos permite ubicar y profundizar en el concepto y en las competencias que se trabajan en la unidad PISA que se usa de modelo en cada uno de los recursos.
Todos los recursos interactivos guardan un diseño estructural uniforme:
En el proyecto curricular de la ESO se incluye el estudio de el Movimiento , introducirlo como tema inicial o como ejemplificación del Método Científico en 3º de la ESO tiene la doble finalidad de evaluar los conocimientos aquiridos sobre el tema, propiamente dicho y sobre la habilidad de cálculo con fracciones y simplificación de fórmulas, además de mostrar la explicación científica de los fenómenos que se observan frecuentemente en vivo y en las retransmisiones televisivas.
Esta unidad fue justificada teóricamente para la elaboración de las pruebas PISA de 2000 - 2003 en el área de las ciencias aplicadas y en los temas relacionados con el movimiento. Este trabajo es una interpretación libre de esas indicaciones, motivada por el auge de las retransmisiones de pruebas de competición en las que están presentes los conceptos de Espacio, Tiempo y Velocidad.
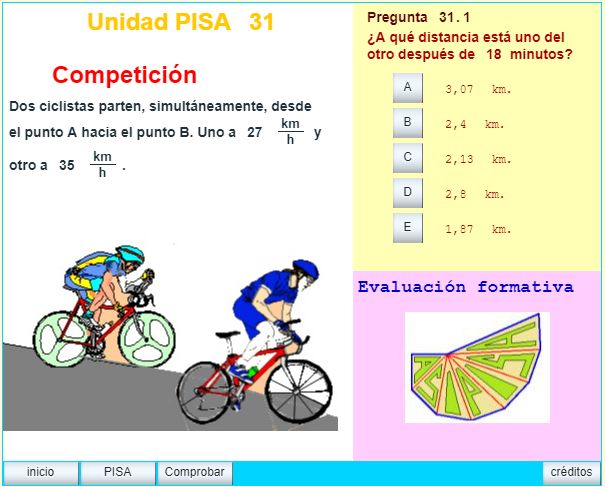
Clasificación PISA:
|
En esta unidad PISA se han introducido los siguientes niveles de aleatoriedad, que permiten profundizar en diferentes aspectos:
|
En el proyecto curricular de la ESO se incluye el estudio de las PROGRESIONES ARITMÉTICAS, introducirlo como tema inicial o como ejemplificación del Método Científico en 3º de la ESO tiene la doble finalidad de evaluar los conocimientos aquiridos sobre el tema, propiamente dicho y sobre la habilidad de cálculo las relaciones entre el Álgebra y la Geometría. Esta unidad fue justificada teóricamente para la elaboración de las pruebas PISA de 2000 - 2003 en el área de las ciencias aplicadas y en los temas relacionados con la forma y el cálculo.
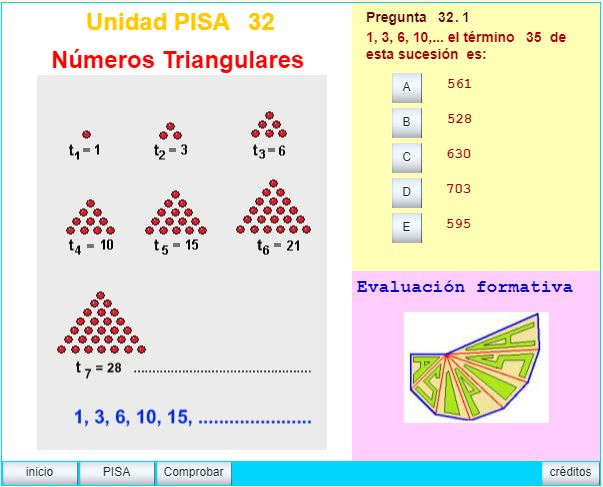
Clasificación PISA:
|
En esta unidad PISA se han introducido los siguientes niveles de aleatoriedad, que permiten profundizar en diferentes aspectos:
|
En el proyecto curricular de la ESO se incluye el estudio de las PROGRESIONES GEOMÉTRICAS, introducirlo como tema inicial o como ejemplificación del Método Científico en 3º de la ESO tiene la doble finalidad de evaluar los conocimientos aquiridos sobre el tema, propiamente dicho y sobre la habilidad de cálculo con fracciones y simplificación de fórmulas, además de mostrar las relaciones entre el Álgebra y la Geometría. Esta unidad fue justificada teóricamente para la elaboración de las pruebas PISA de 2000 - 2003 en el área de las ciencias aplicadas y en los temas relacionados con la forma, la interpretación de los fenómenos físicos y el cálculo.
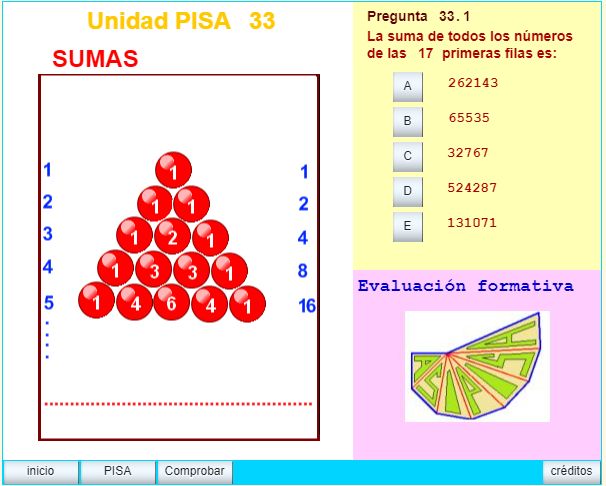
Clasificación PISA:
|
En esta unidad PISA se han introducido los siguientes niveles de aleatoriedad, que permiten profundizar en diferentes aspectos:
|
En el proyecto curricular de la ESO se incluye el estudio de los POLINOMIOS Y ECUACIONES, introducirlo como tema inicial o como ejemplificación del Método Científico en 3º de la ESO tiene la doble finalidad de evaluar los conocimientos aquiridos sobre el tema, además de mostrar la expresión científica (Matemática) de fenómenos que se observan en la vida real. Fue justificada teóricamente para la elaboración de las pruebas PISA de 2000 - 2003 en el área de las ciencias aplicadas en los temas relacionados con el conocimiento científico y la manipulación de expresiones matemáticas.
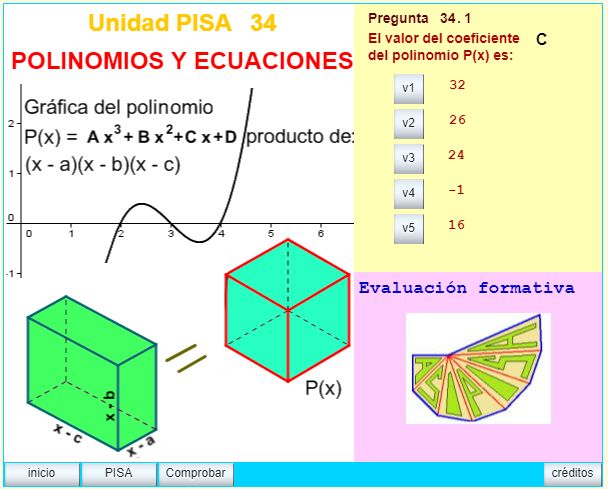
Clasificación PISA:
|
En esta unidad PISA se han introducido los siguientes niveles de aleatoriedad, que permiten profundizar en diferentes aspectos:
|
En el proyecto curricular de la ESO se incluye el estudio de los SISTEMAS DE ECUACIONES, introducirlo como tema inicial o como ejemplificación del Método Científico en 3º de la ESO tiene la doble finalidad de evaluar los conocimientos aquiridos sobre el tema, además de mostrar la explicación científica de los fenómenos que se observan frecuentemente en vivo. Fue justificada teóricamente para la elaboración de las pruebas PISA de 2000-2003 en el área de las ciencias aplicadas en los temas relacionados con la observación científica de situaciones reales y su traducción a lenguaje algebraico.
Clasificación PISA:
|
En esta unidad PISA se han introducido los siguientes niveles de aleatoriedad, que permiten profundizar en diferentes aspectos:
|
En el proyecto curricular de la ESO se incluye el estudio de las FUNCIONES Y GRÁFICAS (La función Cuadrática), introducirlo como tema inicial o como ejemplificación del Método Científico en 3º de la ESO tiene la doble finalidad de evaluar los conocimientos aquiridos sobre el tema, además de mostrar la explicación científica de los fenómenos que se observan frecuentemente en vivo. Fue justificada teóricamente para la elaboración de las pruebas PISA de 2000-2003 en el área de las ciencias aplicadas en los temas relacionados con el conocimiento científico y la manipulación de expresiones matemáticas.
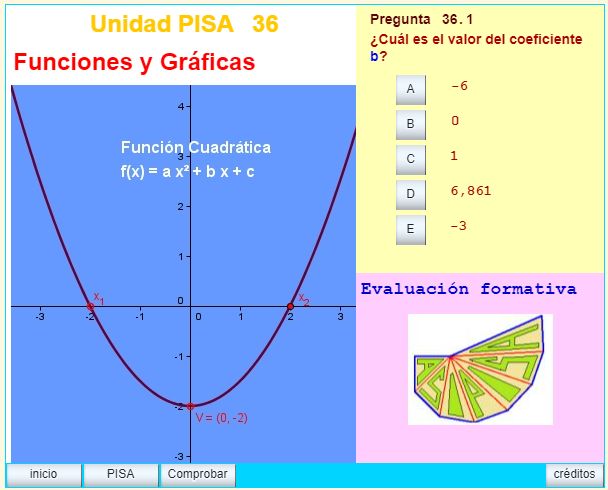
Clasificación PISA:
|
En esta unidad PISA se han introducido los siguientes niveles de aleatoriedad, que permiten profundizar en diferentes aspectos:
|
En el proyecto curricular de la ESO se incluye el estudio del Movimiento y las relaciones entre las distintas magnitudes que intervienen, así como las diferentes unidades usadas para medir esas relaciones. Fue justificada teóricamente para la elaboración de las pruebas PISA de 2000-2003 en el área de las ciencias aplicadas en los temas relacionados con el movimiento.
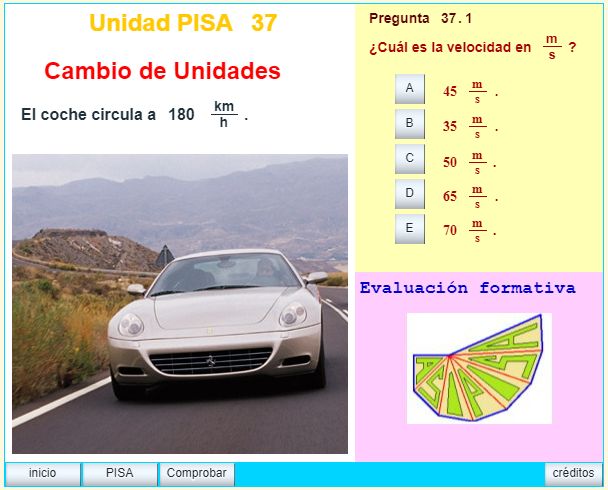
Clasificación PISA:
|
En esta unidad PISA se han introducido los siguientes niveles de aleatoriedad, que permiten profundizar en diferentes aspectos:
|
En el proyecto curricular de la ESO se incluye el estudio de el Movimiento circular y se introduce como tema inicial o como ejemplificación del Método Científico en 3º de la ESO. Fue justificada teóricamente para la elaboración de las pruebas PISA de 2000 - 2003 en el área de las ciencias aplicadas en los temas relacionados con el movimiento.
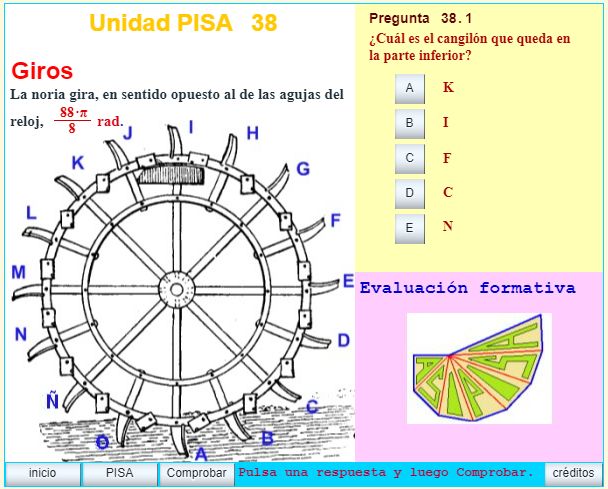
Clasificación PISA:
|
En esta unidad PISA se han introducido los siguientes niveles de aleatoriedad, que permiten profundizar en diferentes aspectos:
|
Ermita de Nuestra Señora de los Santos en el pueblo de Móstoles, Madrid (Rodelar, CC BY-SA 4.0).
Fuente de Los Leones restaurada en Priego de Córdoba, España (El Pantera, CC BY-SA 4.0).
El proyecto Competencias de RED Descartes comprende objetos de aprendizaje interactivos cuyo objetivo es la formación y evaluación competencial. Sus contenidos se basan en las unidades liberadas de PISA, en las de las Pruebas de Evaluación de Diagnóstico de diferentes Comunidades autónomas españolas de acuerdo a leyes educativas españolas. Aunque el objetivo inicial y único de dichas unidades es la evaluación también pueden usarse en el contexto formativo, pero con una gran limitación causada por el hecho de ser estáticas, es decir, constan de un planteamiento, enunciado, preguntas y datos que son fijos. Consecuentemente, una vez que el alumnado conoce la respuesta, éste no puede reutilizar dicha unidad para aprender, pues sería abordar una mera reproducción.
Pero con Descartes esas unidades se reconvierten y adquieren dinámismo e interactividad, permitiendo a sus usuarios la adquisición de competencias. Por tanto, pasamos de un recurso informativo a uno formativo y como complemento, si se desea, sigue sirviendo adicionalmente como un instrumento para la evaluación.
Este proyecto se desarrolló en varias fases y bajo diferentes patrocinios, el propio de RED Descartes, el del Instituto Nacional de Evaluación Educativa (INEE) del Ministerio de Educación de España y del Instituto Nacional de Tecnologías Educativas y Formación del Profesorado (INTEF), que es también otro organismo del Ministerio de Educación español.
En la web de este proyecto se puede consultar una descripción detallada del mismo, un manual de usuario y todos los recursos interactivos que lo conforman.
Ildefonso participó en este proyecto en un encargo que nos realizó el INTEF en 2017 y donde desarrollamos un total de 150 objetos interactivos (75 en versión original y 75 en versión aleatorizada con corrección automática y con descarga, envío por correo eléctronico y/o impresión de las respuestas dadas por el usuario junto a la corrección automática de las mismas). La fuente de los contenidos de estos recursos se sitúan en pruebas PISA liberadas correspondientes a diferentes ediciones de este programa internacional, algunas fueron diseñadas originalmente para la modalidad de evaluación con papel y otras en la modalidad de evaluación con ordenador.
Junto a Ildefonso participaron trece socios más de RED Descartes, y él se responsabilizó del desarrollo de diez de ellos (5 en versión original y 5 en versión aleatorizada con envío, descarga e impresión).
Cada uno de estos objetos interactivos cuentan con una página descriptiva a la que se accede pulsando el botón de información ubicado en la parte superior.
Pulse sobre la siguiente imagen para acceder al contenido informativo de este objeto:
La modalidad de este objeto etiquetada como "Versión original" no contiene aleatoriedad, se presenta fiel a la unidad original PISA y lo que añade es la corrección de las respuestas dadas por el usuario.
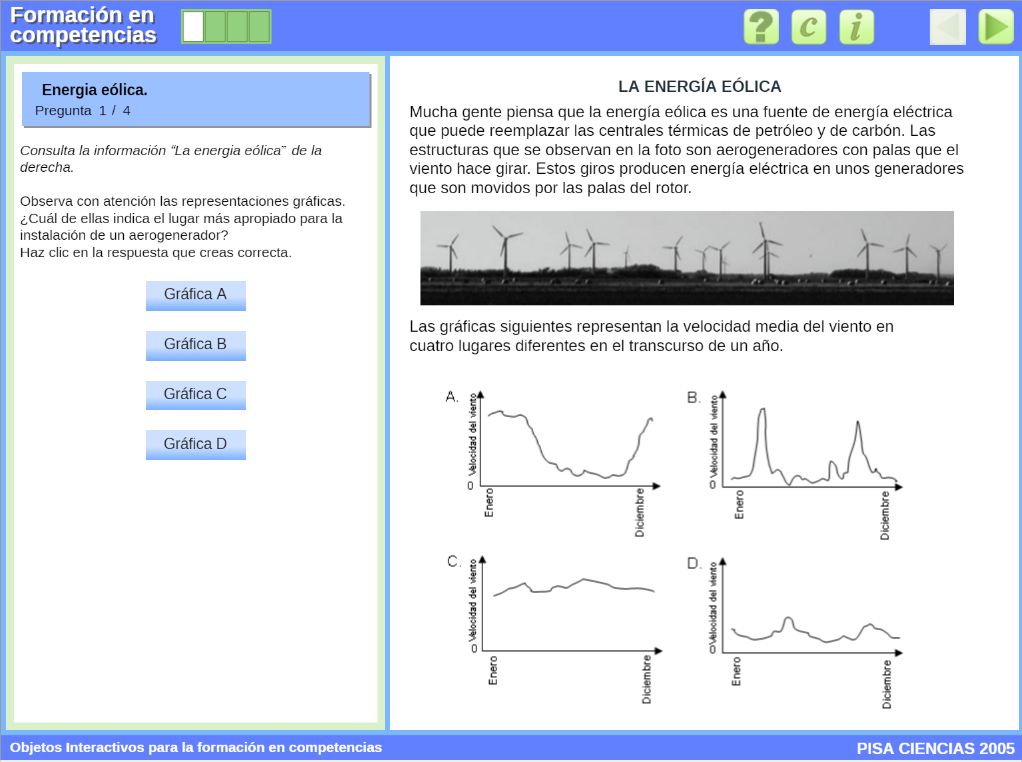
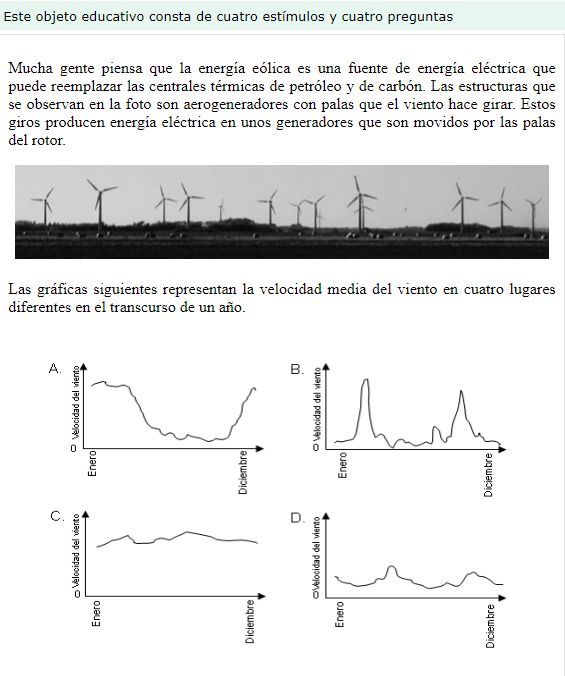
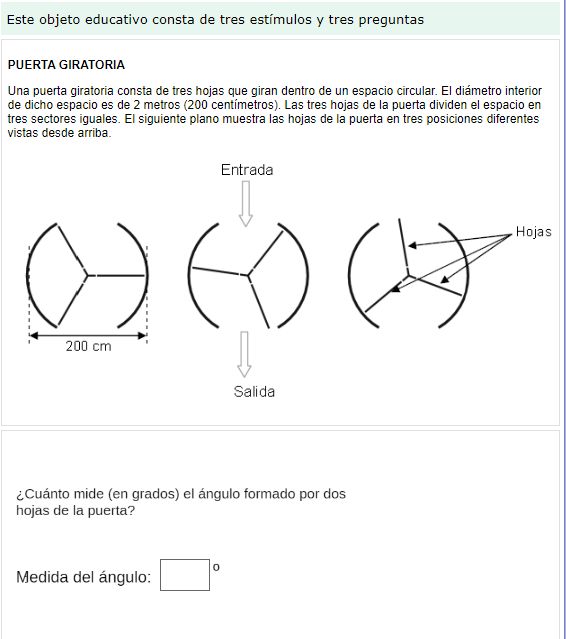
Y a continuación la versión original:
Fuente del rey en 1940, Priego de Córdoba (Rafael Linares Galisteo, CC0).
Imagen de portada del capítulo: Ildefonso y Proyecto Miscelánea.
Fuente en Plaza de la Cultura en el pueblo de Móstoles, Madrid (Zarateman, CC0).
Miscelánea es un subproyecto del proyecto Descartes que recoge escenas aisladas que tratan aspectos muy variados del currículo de Matemáticas y que pueden servir para que el profesorado las utilice directamente para ilustrar conceptos y técnicas básicas, o para que construyan con ellas actividades y propuestas de trabajo en el aula. Pretende ser una caja de herramientas matemáticas que el docente puede utilizar como apoyo y refuerzo al trabajo diario. El profesorado podrá disponer de escenas para crear sus propias lecciones, creando actividades para que el alumnado investigue, deduzca y llegue a conclusiones por sí mismo.
Todas las misceláneas tienen un diseño estructural muy similar: generalmente incluye una escena digital interactiva realizada en DescartesJS y un enlace de Indicaciones que permite abrir una página HTML con la documentación necesaria contenida en tres apartados:
Ildefonso aportó al subproyecto Miscelánea un total de veintidós títulos dedicados a la geometría y la probabilidad, con una excepción, que es la que presentamos en primer lugar en el apartado de "Materiales desarrollados" dedicada al desarrollo del cálculo mental.
Sin duda su tema favorito fue la geometría, bien desarrollando algunos problemas clásicos de la antigüdad (duplicación del cubo, trisección del ángulo y las cuadraturas), los lugares geométricos o las teselaciones del plano.
Dedicó varios trabajos al estudio de las espirales y entroncó con la proporción cordobesa que le condujo a trabajar colaborativamente en el estudio relativo al crecimiento cordobés del Nautilus Pompilius. Sobre todos estos temas iremos exponiendo a lo largo de este capítulo.
"Dos amigos transportaban 8 litros de agua. En el transcurso del camino perdieron su amistad y tuvieron que repartirse los 8 litros en partes iguales, cuatro para cada uno. Sólo disponían de la vasija de 8 litros y de otras dos de 5 y 3 litros. ¿Cómo lo hicieron?"
La escena simula esta situación de repartir en dos partes iguales el agua contenida en una vasija, utilizando junto con la primera otras dos vasijas vacías de distinta capacidad.
Esta miscelánea publicada en 2014, es de las primeras aportaciones de Ildefono al subproyecto y que tuvo a Ángel Cabezudo Bueno como coautor, representa una versión actualizada y muy reformada, en cuanto a diseño, codificación y actividades propuestas, de la original titulada "Trasvasando líquidos" de Salvador Calvo-Fernández Pérez
realizada en una versión Java, anterior, de Descartes. No se puede, por lo dicho, considerar que esta miscelána fue exclusivamente una adaptación a DescartesJS.
Su objetivo es practicar el cálculo mental y desarrollar la capacidad de elaborar estrategias para resolver problemas.
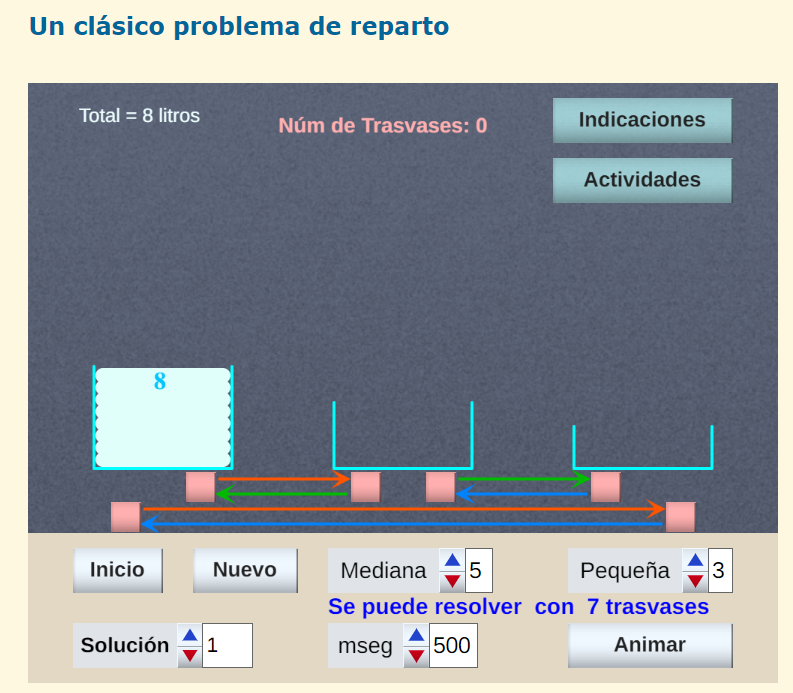
Clasificación:
Razón Cordobesa. El "Número Cordobés".
La proporción (razón) cordobesa es la razón (proporción) entre el radio de la circunferencia circunscrita al octógono regular y el lado de dicho octógono. Esta razón es el denominado número Cordobés
$$\theta = \frac{1}{\sqrt{2-\sqrt{2}}} \thickapprox 1.30656$$ que al igual que el número de Oro, el número de Plata, $\pi$, $e$, $\sqrt{2} $ y otros es también irracional.
Si se tiene interés en conocer la justificación del nombre de la proporción humana o cordobesa de forma pormenorizada, histórica y técnicamente fundamentada, debemos leer el apasionante documento del arquitecto Rafael de la Hoz Arderius, quien introdujo ésta en su artículo La proporción cordobesa de 1973. Puede también consultarse en este documento (Hoz Arderius, La proporción cordobesa, 1996). Un resumen del artículo está contenido en nuestra unidad didáctica Las Matemáticas en la Belleza y la Belleza de las Matemáticas.
En un triángulo isósceles con ángulo desigual de 45º, la razón entre el lado igual y el desigual es el número cordobés.
Un rectángulo se dice que tiene proporción Humana o Cordobesa, si la razón entre el lado mayor y el menor es el número cordobés.
La solución positiva de la ecuación bicuadrada $2x^4-4x^2+1=0$, es también el número cordobés.
Objetivos que se fijan en esta miscelánea:
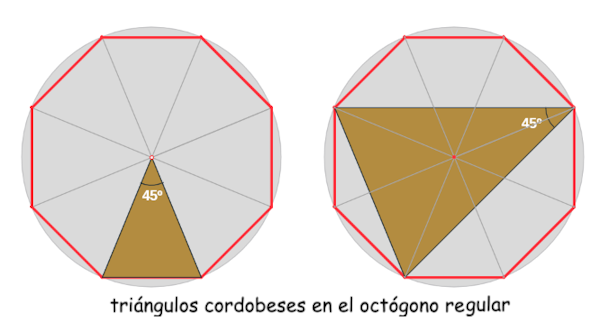
Clasificación:
Los objetivos de esta miscelána son, aprender a construir rectángulos con proporcionalidad Humana o Cordobesa e interesar por los cánones de belleza.
Se dan dos métodos paso a paso para obtener rectángulos con la proporción Humana o Cordobesa.
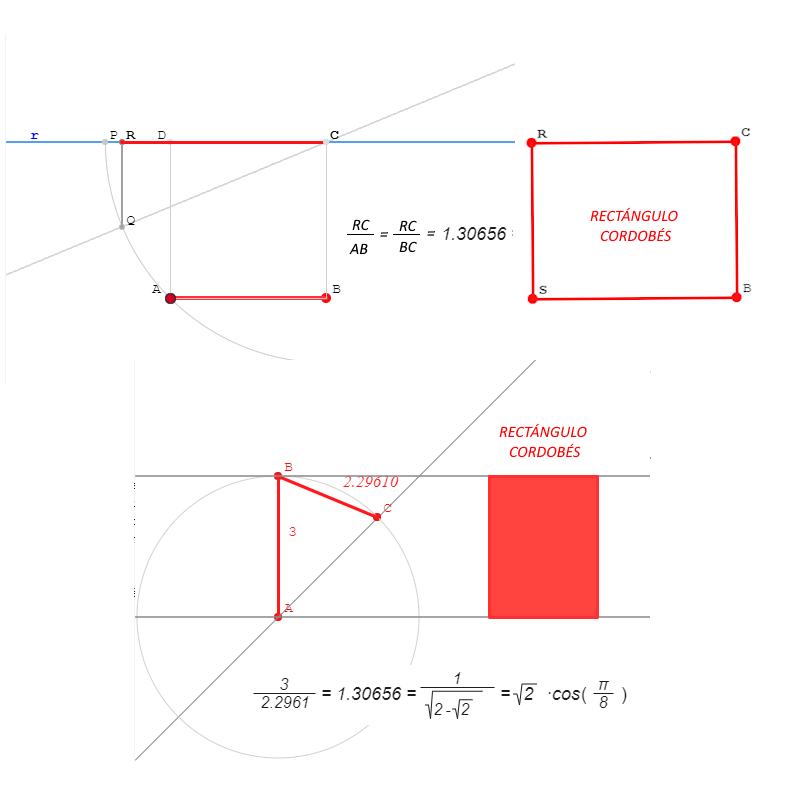
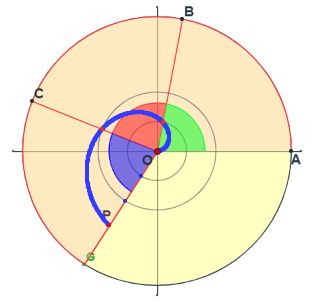
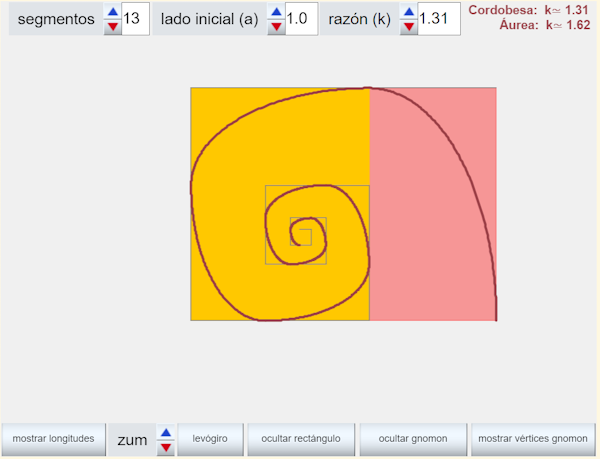
Dado un rectángulo cordobés inicial se añade su gnomon, otro rectángulo que se une al anterior por su lado mayor para obtener el siguiente rectángulo cordobés. Este proceso se repite con cada nuevo rectángulo cordobés obtenido. Los extremos de cada gnomon se enlazan con una línea continua y se construye una espiral.
La espiral que recorre los gnomones es la que hemos venido en considerar como espiral Humana o Cordobesa. La solución propuesta en la imagen se construye con trazas elípticas, una generalización de la espiral de Durero.
Se comprueba, finalmente, en este objeto interactivo que la razón entre el radio de la circunferencia que circunscribe a un octógono y el lado de éste es el número cordobés.
Clasificación:
El crecimiento gnomónico es el que se produce manteniendo la forma o proporción de un objeto (semejanza). Se manifiesta, por ejemplo, en los tejidos más consistentes de los animales como los huesos, los dientes, los cuernos o conchas.
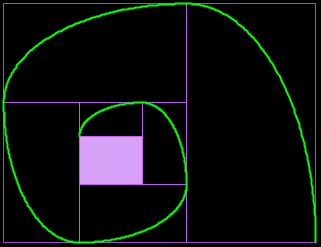
La espiral de Durero se basa en el crecimiento gnomónico discreto de rectángulos aúreos recíprocos y puede dibujarse con regla y compás al ser una concatenación de arcos de circunferencia.
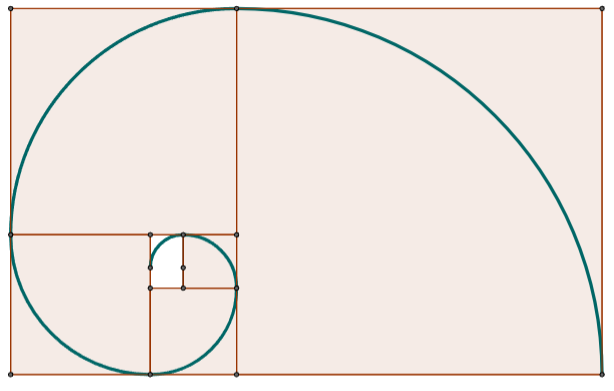
En la siguiente escena del presente objeto interactivo se muestra cómo puede generalizarse la espiral de Durero al considerar un crecimiento gnomónico discreto en base a una sucesión de rectángulos recíprocos, asociados a una determinada razón. En estos casos los gnomones son rectángulos y se concatenan arcos de elipses. Son espirales generalizadas de Durero ya que siguen una pauta de construcción análoga y cuando la razón considerada es la aúrea, entonces la espiral obtenida es la de Durero.
Hay que reseñar que ni la espiral de Durero, ni las generalizadas aquí descritas son espirales logarítmicas.
Los objetivos que se fijan en esta miscelánea son:
Clasificación:
La espiral de Arquímedes fue estudiada y descrita por éste en su libro "Sobre las espirales" en torno al 225 a.C. Esta es la definición que el mismo Arquimedes dió:
"Si una línea recta que permanece fija en un extremo, se la hace girar en el plano con velocidad constante y, al mismo tiempo, se mueve un punto sobre la recta con velocidad constante comenzando por el extremo fijo, el punto describe en el plano una espiral"
Puede definirse de manera dinámica como el resultado de la composición de un movimiento rectilíneo uniforme y de un movimiento circular uniforme. Este procedimiento constructivo es el que se expone en la escena de este recurso interactivo.
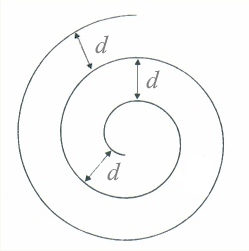
La característica de la espiral de Arquímedes es que entre dos espiras, la distancia es la misma, la expansión y la rotación tienen lugar a la misma velocidad, el vínculo entre ellas es lineal.
Un ejemplo de esta espiral lo encontramos al enrollar una cuerda sobre si misma. Es por tanto muy sencilla de construir y aparece también mucho en la cerámica popular.
A partir de la construcción dinámica o dependiente del tiempo, puede obtenerse la relación algebraica que verifican todos los puntos de esa curva. Ésta queda representada de una manera simple al usar coordenadas polares.
$$ \begin{equation} \begin{matrix} r \hspace{8pt}distancia\, polar\\ \theta \hspace{8pt}ángulo\, polar \hspace{12pt}& r=a+b\cdot\theta\\ a,\,b \in R \hspace{44pt} \end{matrix} \end{equation}$$Los objetivos que se fijan en esta miscelánea son:
Clasificación:
La espiral equiangular, logarítmica o geométrica fue estudiada por Descartes al plantearse la búsqueda de una curva con comportamiento análogo a la circunferencia, en el sentido de que en cada punto el ángulo que forme el radio vector con la tangente sea siempre constante. Bernouilli la denominó "Spira mirabilis" o espiral maravillosa. Puede definirse de manera dinámica como el resultado de la composición de un movimiento rectilíneo no uniforme (exponencial) y de un movimiento circular uniforme. Este procedimiento constructivo es el que se refleja en esta escena interactiva.
A partir de la construcción dinámica o dependiente del tiempo, puede obtenerse la relación algebraica que verifican todos los puntos de esa curva. Ésta queda representada de una manera simple al usar coordenadas polares.
$$ \begin{equation} \begin{matrix} r \hspace{8pt}distancia\, polar\\ \theta \hspace{8pt}ángulo\, polar \hspace{12pt}& r=a\cdot b^\theta\\ a,\,b \in R^+ \hspace{42pt} \end{matrix} \end{equation}$$El nombre de logarítmica se justifica porque es una expresión equivalente pues el ángulo queda determinado en función del logaritmo de la distancia polar, es decir del módulo del radio vector.
Los objetivos que se fijan en esta miscelánea son:
Clasificación:
¿La Naturaleza es matemática o matematizamos la Naturaleza? Lo que sí parece obvio es que basta observar nuestro entorno para reconocer atractivas formas naturales y asimilarlas a modelos matemáticos que se mimetizan con ellas.
El Nautilus pompilius (cefalópodo del género Nautilus) es un ejemplo de esa belleza matemática-natural.
Un cefalópodo del orden de los nautílidos (Nautilia) que lleva haciendo matemáticas desde el periodo Devónico (hace más de 400 millones de años) hasta nuestra actualidad, y que nos invita a matematizar. Hecho que es el objeto de esta miscelánea con Descartes: ¿Qué forma tiene la sección de la concha? ¿Por qué adopta esa forma y cómo se genera ésta? Abordemos un breve, pero explicativo, recorrido.
Algunos de los objetivos de esta miscelánea, que se exponen en las "Indicaciones" son:
Clasificación:
Se parte de un triángulo equilátero y se descompone en cuatro polígonos, tres cuadriláteros y un triángulo.
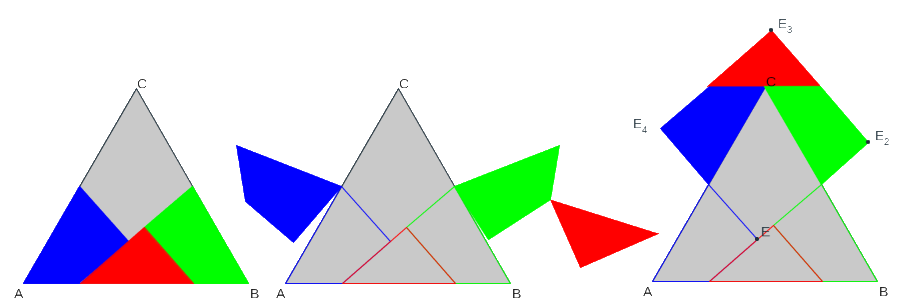
Precisamente esos cuatro polígonos generan la cuadratura del triángulo equilátero dado.
Se indica el proceso constructivo y se puede generar una animación que lleva desde la teselación a la cuadratura: al ir variando el valor del ángulo general del giro, alfa, se puede observar detenidamente como se modifica la situación de cada subpolígono de la teselación hasta formar la cuadratura del triángulo.
En la página de Ildefonso en GeoGebra encontramos una escena titulada Cuadratura de un triángulo cualquiera (método directo II) y en el proceso de construcción del cuadrado de igual área que el triángulo se observa como queda también teselado.
Se puede aplicar este método para el caso que nos ocupa: En el triángulo ABC se halla el punto medio de los lados $a$ y $b$, respectivamente $M_2$ y $M_3$. Se construye la circunferencia de centro $D$, punto medio de $M_2 M_3$. Se elige un punto $E$ en la semicircuferencia inferior y se obtiene su simétrico $E_4$ respecto de $M_3$. Se contruye el cuadrado de lado $EE_4$. Si el área de este cuadrado
coincide con la del triángulo ya tenemos la cuadratura buscada. Es facil dar con este punto pues trabajamos con un software matemático dinámico.
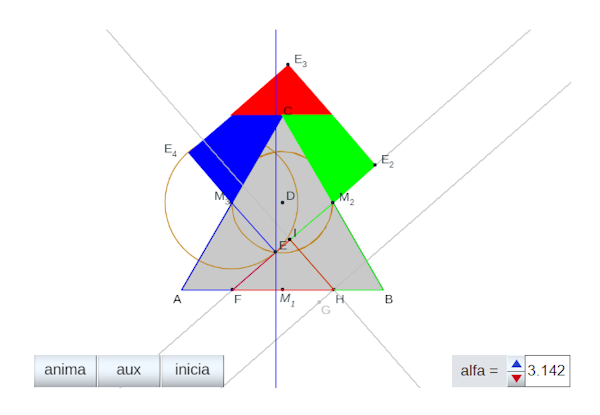
Objetivos
Conocer la existencia del método, practicar con la descomposición de un polígono en subpolígonos que lo teselen y profundizar en el conocimiento de las cuadraturas.
Clasificación:
Los problemas clásicos de la geometría griega son, por activa o por pasiva, fuente inagotable de inspiración. En esta ocasión el estudio de los lugares geométricos nos llevó a sus orígenes por ende a Hípias, Dinostrato, Arquímedes... e inevitablemente a la cuadratura dinámica del círculo, esto es, a la cuadratura de cualquier polígono, regular o no, con cualquier número de lados. Resultando que, aparentemente, en la base de este proceso está el cuadrado. Motivo por el cual decidimos estudiar este polígono.
Ahora bien, al intentar analizar el cuadrado, éste, en sí mismo, parece desaparecer mostrando como en su interior subyacen infinidad de polígonos: triángulos, cuadrados, rectángulos, trapecios, rombos… y una infinidad de otras formas inexistentes, virtuales, cuya proyección a la realidad tangible proporcionan, probablemente, los objetos y formas más útiles, en todos los sentidos, para el ser humano.
Puede comprobarse como el trazo de unas pocas líneas en un cuadrado y a continuación al realizar el teselado del plano con el mismo, aparecen, de manera dinámica, formas que son el resultado de la composición de una traslación y/o de un giro; u otros, y como la visión de conjunto, a veces un palíndromo geométrico bidimensional, sugiere formas, sensaciones y conceptos cambiantes.
Este procedimiento constructivo es el que estas escenas interactivas pretenden analizar aún cuando sea de forma visual.
Objetivos
Clasificación:
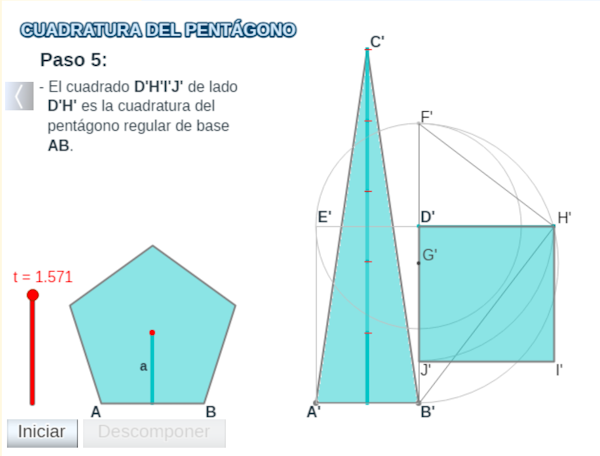
La cuadratura de un pólígono cualquiera y en particular la de un pentágono regular, consiste en determinar un cuadrado que tenga el mismo área que aquel.
Esta cuadratura, siguiendo el método clásico, se basa en que el pentágono, en este caso regular, de lado $AB$, puede descomponerse en cinco triángulos isósceles. La base de cada uno de los triángulos es un lado correspondiente del pentágono y la altura respectiva es la apotema a, de dicho pentágono. El área del pentágono es la suma de las áreas de estos cinco triángulos congruentes y coincide con el área del triángulo isósceles de base uno de los lados del pentágono, p.e. el $AB$ y de altura $5 \cdot a$. Es decir, cuadrar el pentágono de lado $AB$ coincide con cuadrar este último triángulo.
Como podemos observar, la cuadratura de un polígono regular se basa en el método de cuadrar un triángulo y para ello se descompone el polígono en triángulos congruentes con vértice común en el centro del polígono.
La cuadratura del triángulo pasa por cuadrar el rectángulo de área equivalente, con igual base y altura mitad.
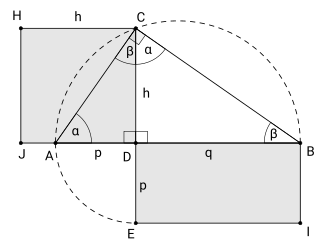
El paso final consiste en obtener el lado del cuadrado de igual área que el rectángulo, como media geométrica de su lado mayor y su lado menor, para ello se dibuja la altura del triángulo rectángulo inscrito en la circunferencia de diámetro suma los dos lados mayor y menor del rectángulo, Teorema de la media geométrica.
Objetivos
Clasificación:
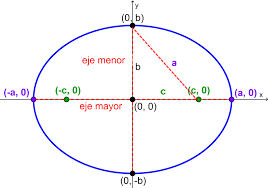
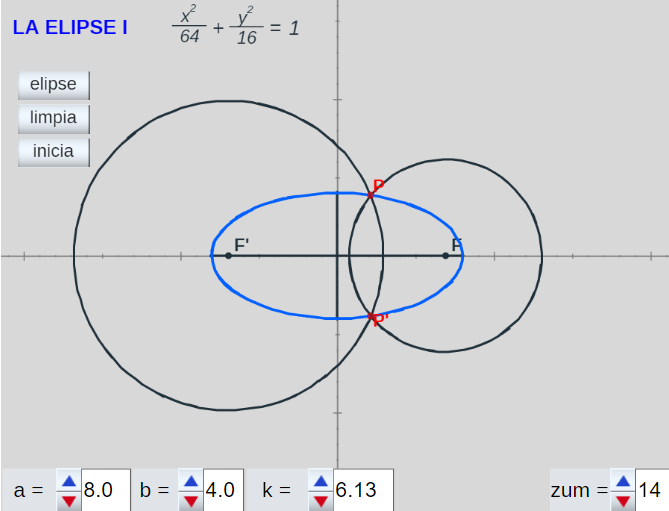
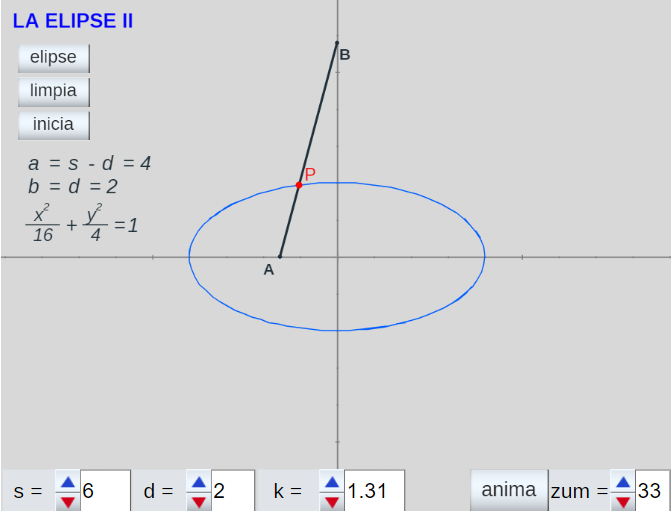
El segmento $AB$ , de longitud $s$, desliza por los ejes pependiculares: el extremo $A$ lo hace apoyado sobre el eje horizontal y el $B$ sobre el vertical. Podemos observar que el lugar geométrico de un punto $P$ de $AB$ que dista $d$ de $A$, cuando $A$ y $B$ realizan su movimiento oscilante sobre su eje correspondiente es una elipse de parámetros $a=s-d \,$ y $\, b=d$
Clasificación:
Objetivo: Conocer la existencia del método, practicar con la generación del lugar geométrico y profundizar en el conocimiento de la elipse.
Una ruleta cicloidal es una curva plana que describe la trayectoria de un punto vinculado a una circunferencia, llamada generatriz, que rueda tangencialmente sin deslizarse sobre otra curva plana llamada directriz. Según sea la curva directriz sobre la que rueda la circunferencia, la ruleta cicloidal recibe nombres diferentes. Se llama cicloide a la ruleta cicloidal que rueda sobre una recta. El punto vinculado a la circunferencia puede ser interior, exterior o estar en la circunferencia; en este último caso se dice que la cicloide es normal.
Objetivos
Si la curva directriz es otra circunferencia y seguimos la trayectoria del punto de contacto inicial entre ambas circunferencias podemos distinguir dos casos:
Objetivos
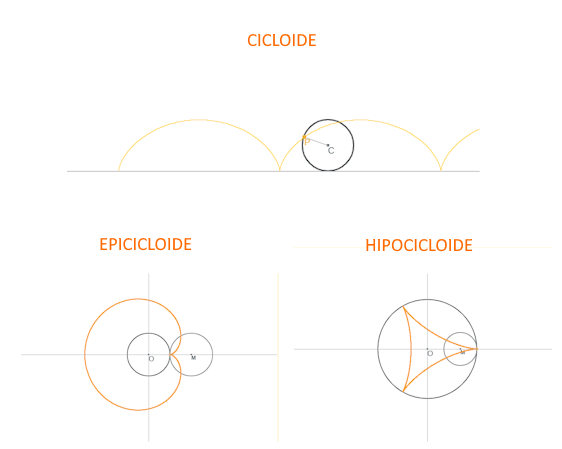
Clasificación:
Esta utilidad muestra de forma muy resumida y esquemática una introducción al estudio de algunas de las soluciones propuestas, en su día, por los geómetras griegos para resolver los problemas mencionados y que, por no cumplir con las normas de 'uso exclusivo de regla y compás', no fueron aceptadas oficialmente.
La concepción dinámica de las entidades geométricas elementales: punto, recta... y la abstracción del concepto de proporción hacen que aquellos geómetras manipularan el número pi (π) y sus partes con absoluta soltura.
Las siguientes escenas son un sincero reconocimiento y homenaje al prodigioso logro de los antiguos geómetras griegos y muestran como el desplazamiento de un punto, bajo ciertas condiciones, genera un lugar geométrico y gracias a las propiedades de este lugar puede trisecarse cualquier ángulo o encontrar la cuadratura de un círculo. Virtualmente los procedimientos son exactos e impecables según muestran las escenas de la miscelánea.
Podemos ver en este objeto interactivo dos aplicaciones de la espiral de Arquímedes: una para trisecar un ángulo y otra para cuadrar el círculo. Esta espiral ha sido tratada en el epígrafe anterior 5.2.5.
Objetivos
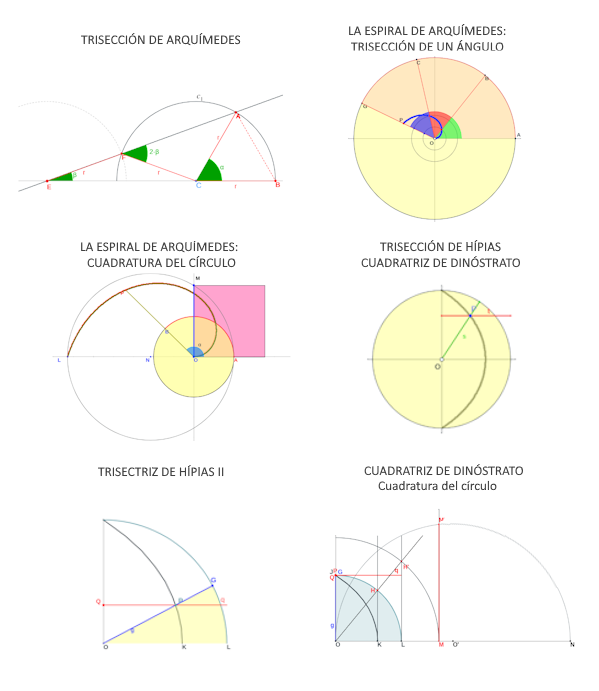
Clasificación:
Dado un cubo de arista $a$, el problema consiste en construir, usando sólo la regla y el compás, la arista $x$ de un cubo cuyo volumen sea el doble del volumen del cubo dado.
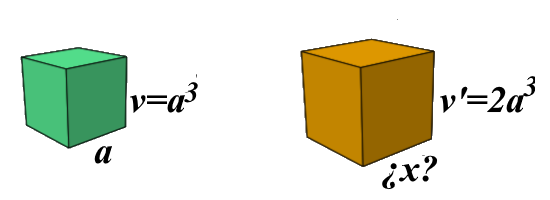
Éste es el enunciado clásico que no pudo ser resuelto por los matemáticos de la antigüedad griega pues la solución pasaba por obtener el valor de la raíz cúbica de $2$; esto no es posible con el método de la regla y el compás y requería el empleo de herramientas y técnicas diferentes.
Hipócrates de Chíos (470–410 aC) demostró que tal problema se reduce a encontrar dos medias proporcionales:
$$\frac{a}{x}=\frac{x}{y}=\frac{y}{2a}$$
pues en estas condiciones se cumplirá que $\; \displaystyle \frac{a^3}{x^3}= \frac{1}{2}$
Objetivos
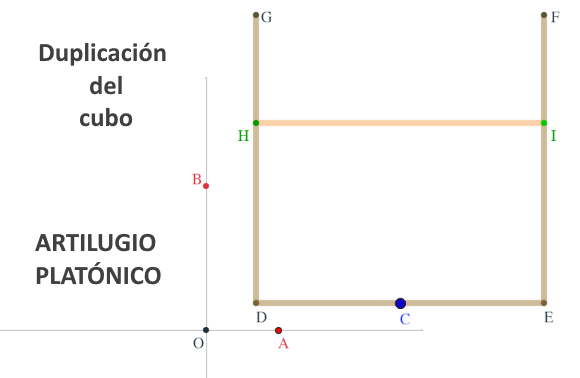
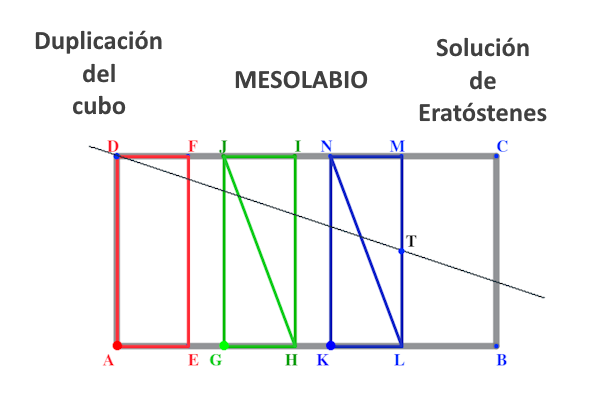
Clasificación:
Las escenas muestran el clásico problema de probabilidad matemática propuesto por el matemático francés Georges Louis Leclerc (1708-1788) conde de Buffon, donde se aplicó la Geometría para su resolución.
En la primera parte se escenifican los resultados del experimento, lanzando una cantidad de agujas determinada, tantas veces como queramos: $2,\, 3,\, 4,\,..., 500,\,..., 1000,\,...,\, 30000$. En las escenas siguientes se analizan los resultados y se justifica, geométricamente, por qué la probabilidad de que la aguja corte a una línea es $\displaystyle \frac{2}{\pi}$
Objetivos
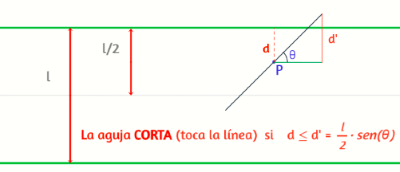
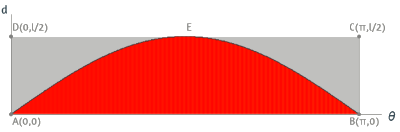
Clasificación:
En una escena inicial se explica como calcular la probabilidad total de un suceso aleatorio compuesto: Se elige al azar una urna entre dos idénticas que no permiten ver su contenido. En cada urna hay un número, en general diferente, de bolas de tres colores, rojo, verde y azul. Elegida una urna a continuación se extrae una bola aleatoriamente y se explica como calcular la probabilidad de que la bola sea de un determinado color. Esta probabilidad está condicionada a que se haya extraido de una u otra urna ya que la probabilidad es diferente para cada urna y de aquí que tengamos que hablar de probabilidad total.
A los efectos de hacer fácilmente un recuento de los distintos resultados del experimento nos valemos de tablas de contingencia y de diagramas de árbol. En la siguiente imagen vemos como serían estos esquemas para el experimento que nos ocupa
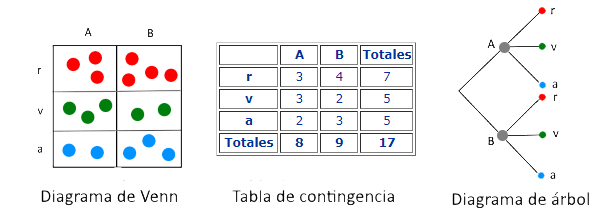
En una segunda escena se plantean distintos problemas de probabilidad total y se solicita su resolución siguiendo las pautas aprendidas.
Objetivos
Clasificación:
En una escena inicial se explica como calcular la probabilidad a posteriori de un suceso aleatorio: Se elige al azar una urna entre tres idénticas que no permiten ver su contenido. En cada urna hay un número, en general diferente, de bolas de tres colores, rojo, verde y azul. Elegida una urna a continuación se extrae de ella una bola aleatoriamente, se muestra su color y se pregunta la probabilidad de que proceda de una, en concreto, de las urnas, de aquí que tengamos que hablar de probabilidad a posteriori esto es del Teorema de Bayes.
En esta miscelánea aplicamos el Teorema de Bayes. Para poder entender y en consecuencia aplicar correctamente este importante teorema de la teoría de Probabilidades es necesario conocer lo que entendemos por probabilidad condicionada y qué es la probabilidad total de un suceso aleatorio. Para ello remitimos al lector a los conceptos aplicados incluidos en la miscelánea del mismo autor publicada en la web Red Descartes y titulada Ejercicios de probabilidad total (página 130 de este libro)
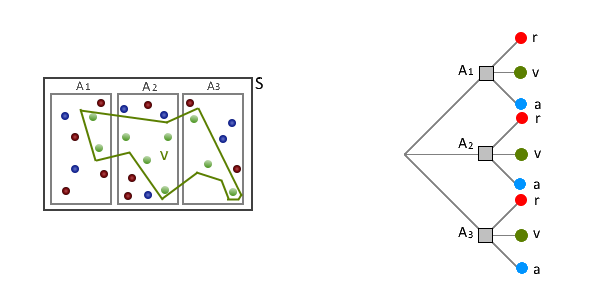
En una segunda escena se plantean distintos problemas de probabilidad a posteriori y se solicita su resolución siguiendo las pautas aprendidas.
Objetivos
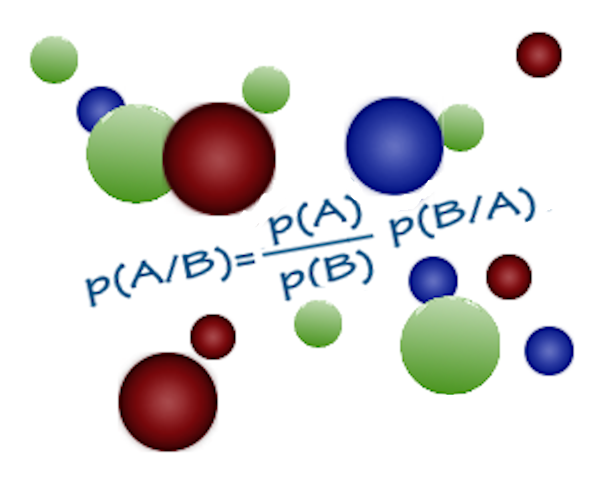
Clasificación:
La distribución normal de probabilidad es sin duda la más importante de las distribuciones continuas pues la mayoría de los fenómenos naturales se comportan básicamente de forma normal; su gráfica se reconoce como "campana de Gauss"
Una distribución Normal de media $\mu$ y desviación típica $\sigma$ se representa por $N(\mu , \sigma)$ y para calcular probabilidades bajo esta campana se procede a tipificar la variable aleatoria pasando a otra distribución Normal $N(0,1)$, cuyos valores ya están tabulados, pudiendo reducir a ésta los calculos de cualquier $N(\mu , \sigma)$ .
Dada una variable aleatoria normal $x → N(\mu , \sigma)$, se tipifica pasando a la variable aleatoria estandar $z → N(0 , 1)$, $\, \displaystyle z= \frac{x-\mu}{\sigma}$
La escena muestra, de forma directa e intuitiva, el valor aproximado (con cuatro cifras decimales) de $P(z≤k)$ donde:
Objetivos
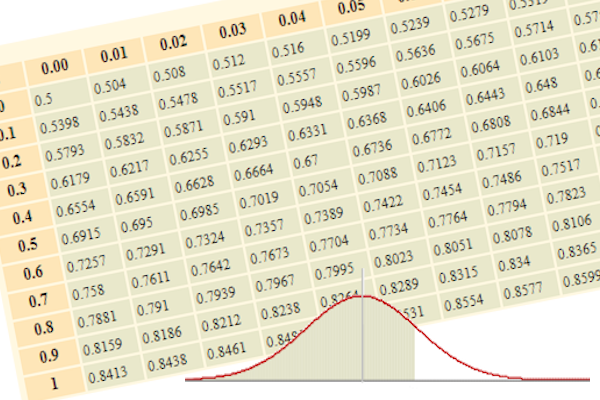
Clasificación:
Imagen de portada del capítulo: página de Ildefonso en GeoGebra.
Imagen de esta página: logo de GeoGebra (pngegg).
En el siguiente video, hacemos un recorrido de la página de Ildefonso en GeoGebra, que al 4 de agosto de 2023 aún está visible.
Son 200 escenas que Ildefonso publica en GeoGebra (versión HTML5), de las cuales presentamos 50 a continuación.
Primera escena publicada por Ildefonso en esta página (13 de noviembre de 2012). La cuadratura del rectángulo es una tarea que consiste en obtener un cuadrado con la misma área que un rectángulo dado (wikiwand).
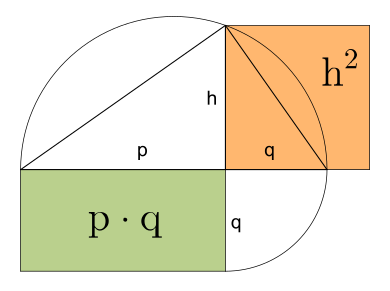
Ildefonso usa el método de las alturas, en el que se asume que un lado es la sección de la hipotenusa $p$ y el otro lado es la sección de la hipotenusa $q$ de un triángulo rectángulo. Luego, se pivota el lado más corto del ángulo recto y se obtiene la base de un triángulo rectángulo. Sobre esta base se aplica el teorema de Tales. La extensión del lado más corto del triángulo rectángulo interseca la circunferencia de Tales y proporciona la altura del triángulo rectángulo con las secciones de hipotenusa $p$ y $q$. Si ahora se construye un cuadrado (aquí naranja) por encima de esta altura, entonces tiene exactamente la misma área que el rectángulo dado.
¡Mueve los puntos $A, B$ o $C$!
Escena publicada por Ildefonso el 5 de junio de 2015. En geometría, la cadena Pappus es un anillo de círculos entre dos círculos tangentes. Fue investigada por Pappus de Alejandría en el siglo III dC. (wikiwand).
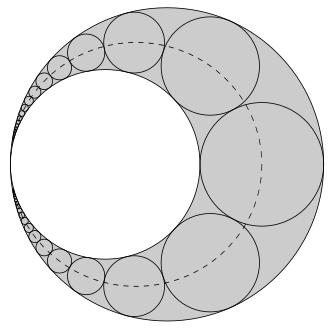
Un arbelos está definido por dos círculos, CU y CV, que son tangentes y donde CU está contenido por CV. Denótense los radios de estos dos círculos como rU y rV, respectivamente, y que sus centros sean los puntos D y F (ver objeto interactivo en la página siguiente). La cadena de Pappus consiste en los círculos en la región blanca, que son tangentes externamente a CU (el círculo interno) y tangentes internamente a CV (el círculo externo). El radio, el diámetro y el centro del enésimo círculo de la cadena Pappus se denotan respectivamente como rn, dn y Pn.
¡Mueve los puntos $A, B$ o $D$!
Un fractal es un objeto geométrico cuya estructura básica, fragmentada o aparentemente irregular, se repite a diferentes escalas. El término fue propuesto por el matemático Benoît Mandelbrot en 1975 y deriva del latín fractus, que significa quebrado o fracturado. Muchas estructuras naturales son de tipo fractal (wikiwand).
Si bien el término "fractal" es reciente, los objetos hoy denominados fractales eran bien conocidos en matemáticas desde principios del siglo xx. Las maneras más comunes de determinar lo que hoy denomi- namos dimensión fractal fueron establecidas a principios del siglo xx en el ámbito de la teoría de la medida.
La escena la puedes ver, haciendo clic sobre la siguiente imagen.
Fecha de publicación: 10 de junio de 2015
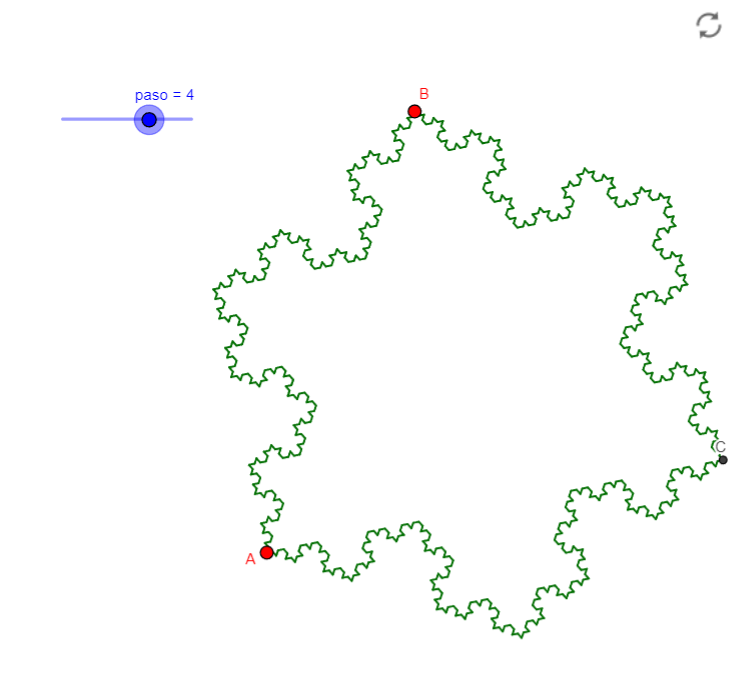
¡Haz clic sobre la imagen!
Entre el 10 y el 12 de junio de 2015, Ildefonso publica más de una decena de escenas relacionadas con el teselado, que él denomina "teselar", tres de ellas las presentamos en la siguiente página.
Los términos teselaciones y teselado hacen referencia a una regularidad o patrón de figuras que recubren o pavimentan completamente una superficie plana. Los teselados se crean usando copias isométricas de una figura inicial, es decir, copias idénticas de una o diversas piezas o teselas con las cuales se componen figuras para recubrir enteramente una superficie. Distintas culturas a lo largo de la historia han utilizado esta técnica para formar pavimentos o muros de mosaicos en catedrales y palacios (wikiwand).
Las escenas seleccionadas las puedes ver, haciendo clic sobre las siguientes imágenes.
|
|
|
|
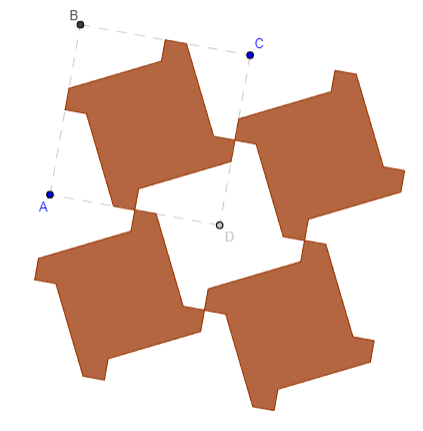
¡Haz clic sobre las imágenes!
El 15 de junio de 2015, Ildefonso publica una animación que simula el proceso automatizado de llenado, el cual hace parte de la producción en cadena o producción en serie, proceso revolucionario en la producción industrial cuya base es la cadena de montaje, línea de ensamblado o línea de producción, tal como se observa en este video:
¡Haz clic en Inicio!
El 15 de junio de 2015, Ildefonso publica la escena "Motor de explosión de un cilindro", que acompaña con otra denominada "Sincronización de Movimientos" Un motor de explosión es un tipo de motor de combustión interna que utiliza la explosión de un combustible, encendido de manera provocada mediante una chispa, para expandir un gas que empuja un pistón, el cual está sujeto al cigüeñal por una biela, esta hace las veces de manivela y transforma el movimiento lineal del pistón en rotativo en el cigüeñal. El ciclo termodinámico utilizado es conocido como ciclo Otto. Existen motores de explosión de dos tiempos y de cuatro tiempos (Wikipedia).. La segunda escena, Ildefonso la describe así:
El estudio del movimiento y en particular el de la transformación del movimiento rectilíneo en circular es una excusa extraordinaria para repasar y aplicar los conceptos curriculares referentes al estudio de los ángulos, de su medida, de las razones trigonométricas de dichos ángulos y de la aplicación, en la práctica, de todos estos conceptos.
En la siguiente página, haz clic sobre las imágenes para ver estas dos escenas.
|
|
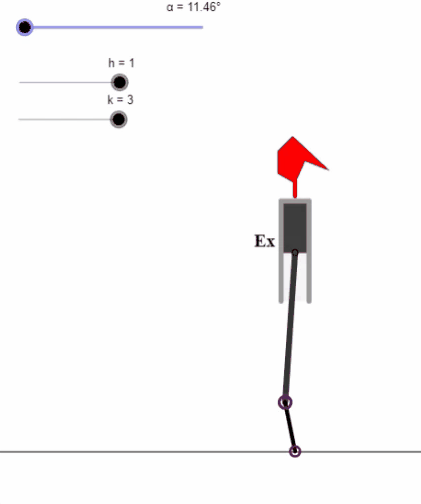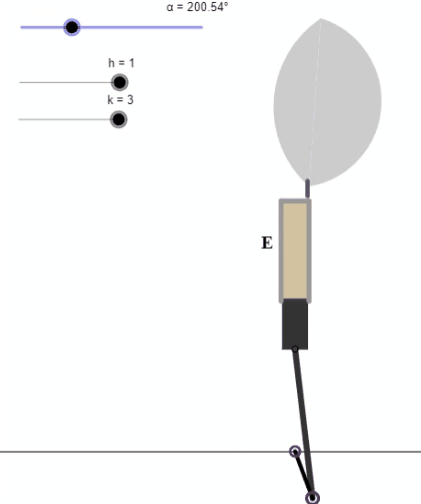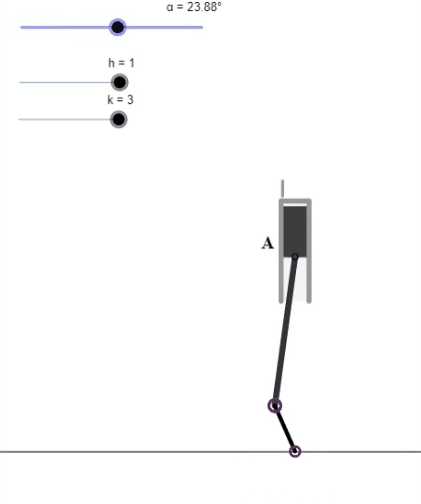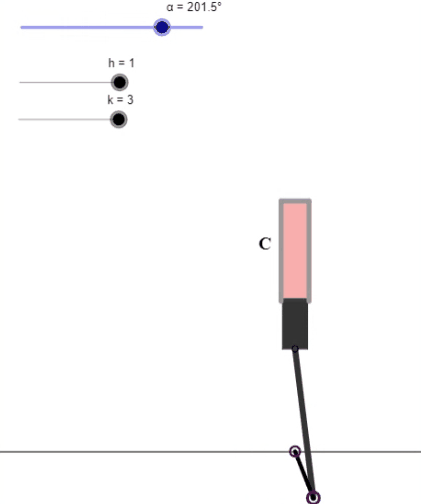
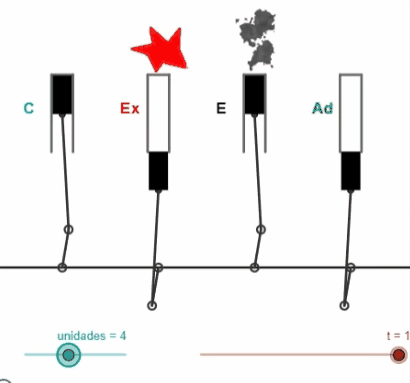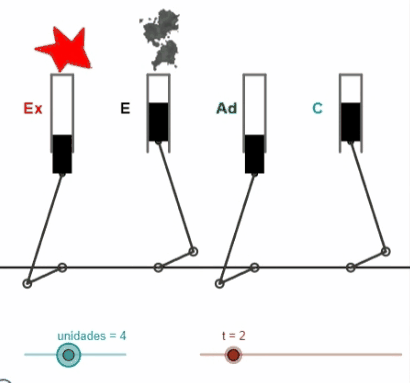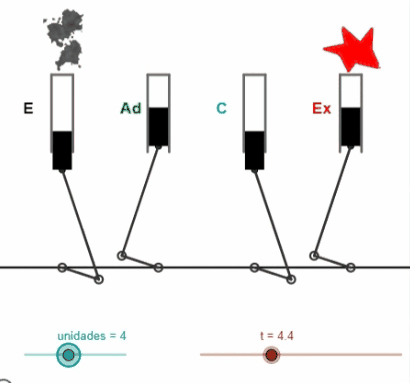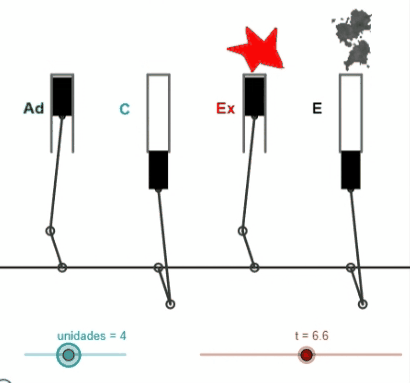
¡Haz clic sobre las imágenes!
Ildefonso establece como objetivo: "El estudio de los motores de explosión, de cuatro tiempos y de hasta 8 cilindros" Este motor, también llamado motor de gasolina o motor Otto, es junto al motor diésel, el más utilizado hoy en día para mover vehículos autónomos de transporte de mercancías y personas. El combustible que se usa tradicionalmente en un motor de explosión es la gasolina. Actualmente, algunos motores de explosión pueden funcionar también con etanol, gas natural comprimido, gas licuado del petróleo o hidrógeno, además de gasolina (Ibid.)..
Entre el 17 y 19 de junio de 2015, Ildefonso publica 10 escenas sobre los ángulos en la circunferencia, de las cuales hemos seleccionado cuatro.
En la siguiente página, haz clic sobre las imágenes para ver estas cuatro escenas.
|
|
|
|
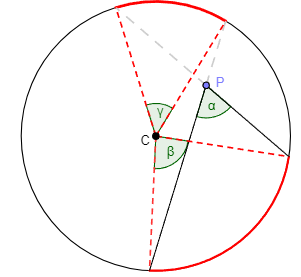
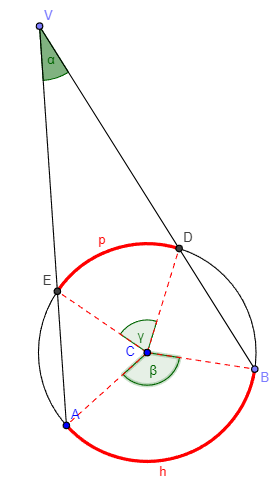
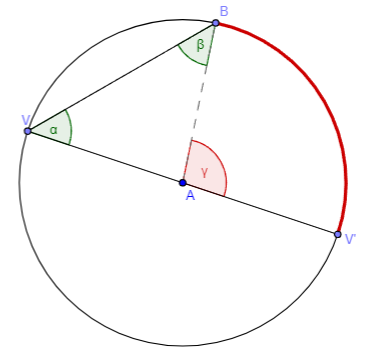
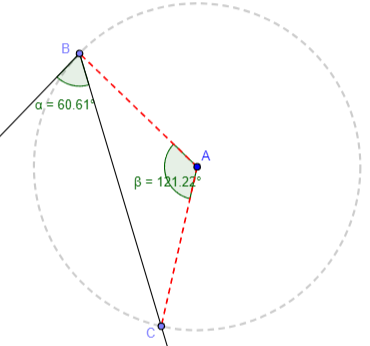
¡Haz clic sobre las imágenes!
Apolonio de Perge o Perga (Perge, c. 262 a. C. - Alejandría, c. 190 a. C.) fue un matemático y astrónomo griego famoso por su obra sobre las secciones cónicas. Él fue quien dio el nombre de elipse, parábola e hipérbola, a las figuras que conocemos. Logró solucionar la ecuación general de segundo grado por medio de la geometría cónica. También se le atribuye la hipótesis de las órbitas excéntricas o teoría de los epiciclos para intentar explicar el movimiento aparente de los planetas y de la velocidad variable de la Luna. Sus extensos trabajos sobre geometría tratan de las secciones cónicas y de las curvas planas y la cuadratura de sus áreas. Recopiló su obra en ocho libros y fue conocido con el sobrenombre de "El Gran Geómetra".
Entre el 20 y el 22 de junio de 2015, Ildefonso publica 10 escenas sobre "El Gran Geómetra", de las cuales presentamos cuatro.
|
|
|
|
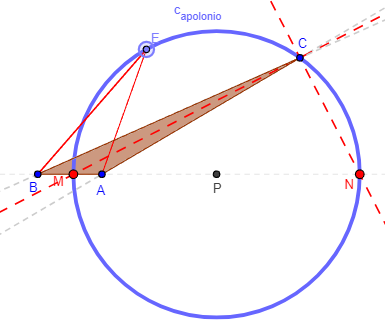
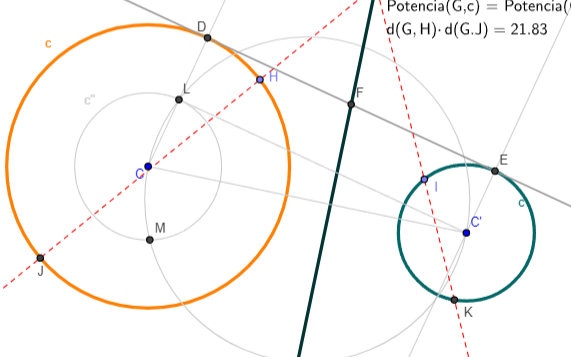
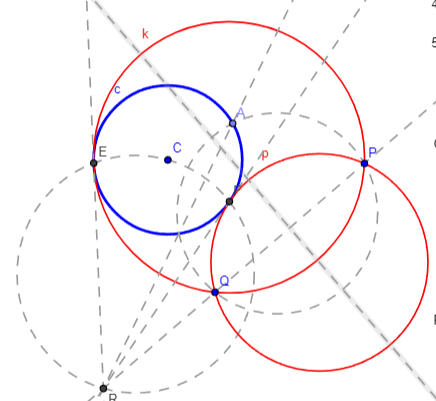
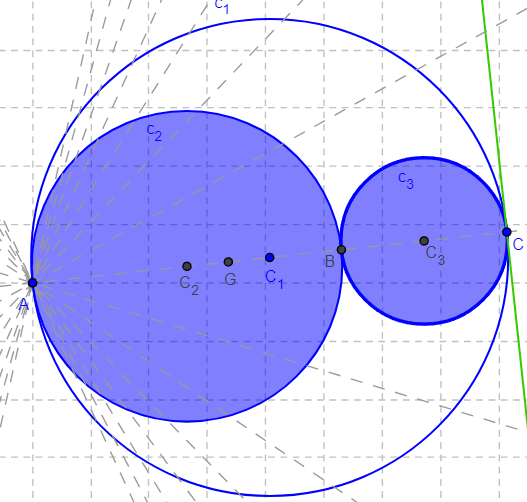
¡Haz clic sobre las imágenes!
El estudio de las espirales en la naturaleza tiene una larga historia que se remonta a Christopher Wren, quien observó que muchas conchas animales formaban una espiral logarítmica. En Sobre el creci- miento y la forma, D'Arcy Wentworth Thompson examina exhaustivamente estas espirales. Describe cómo las conchas se forman siguiendo una curva que rota en torno a un eje, de modo que la forma de la curva permanece constante pero su tamaño aumenta en progresión geométrica. En algunas conchas como nautilus y las amonites la curva generatriz gira en un plano perpendicular al eje y la concha se conforma como figura discoidal plana. En otras sigue un patrón espacial, con forma de hélice. La isla de Célebes, en el Pacífico, nos da una idea de figura en espiral (Wikiwand).
Entre el 22 de junio y el 27 de agosto de 2015, Ildefonso publica nueve espirales, que presentamos a continuación.
|
|
|
|
|
|
|
|
|
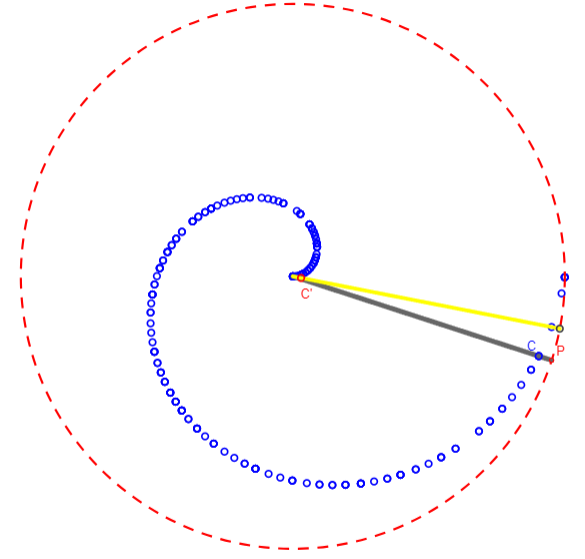
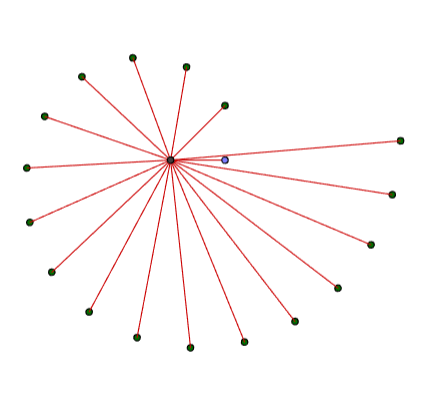
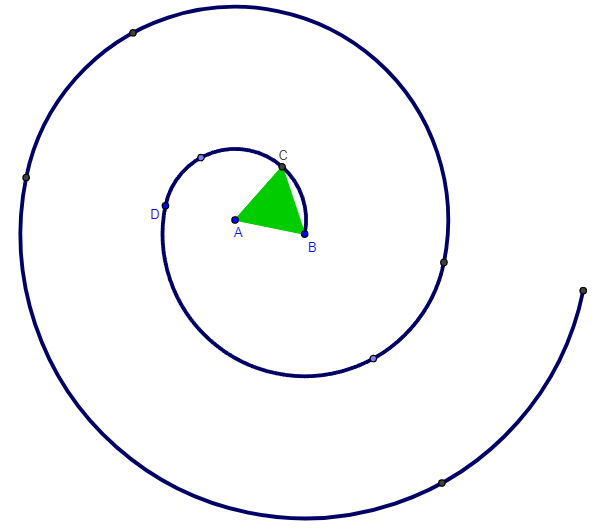
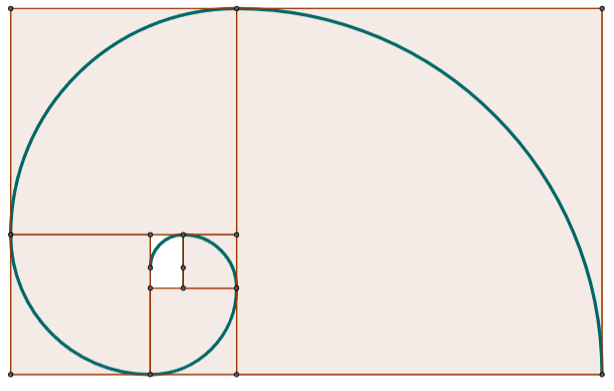
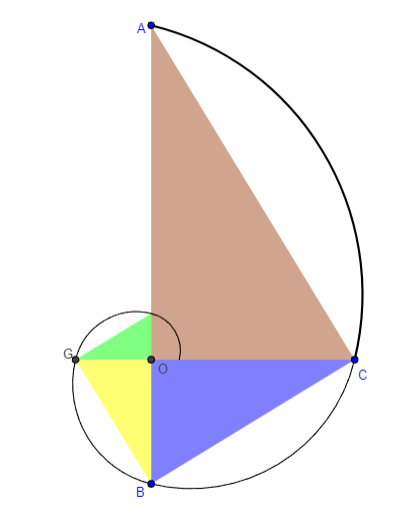
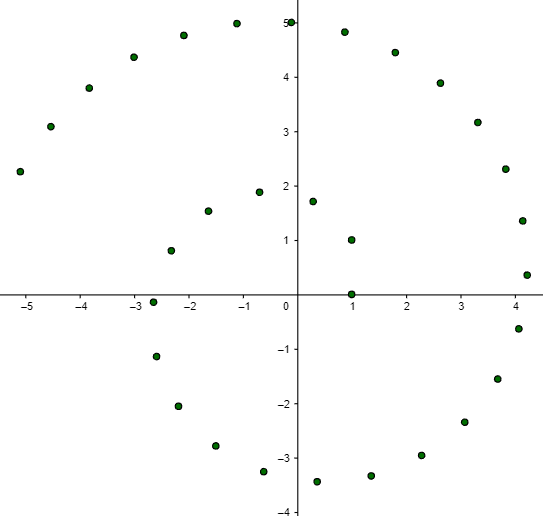
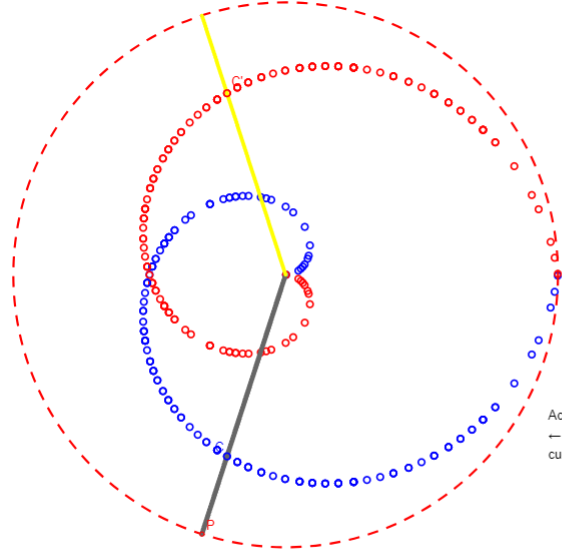
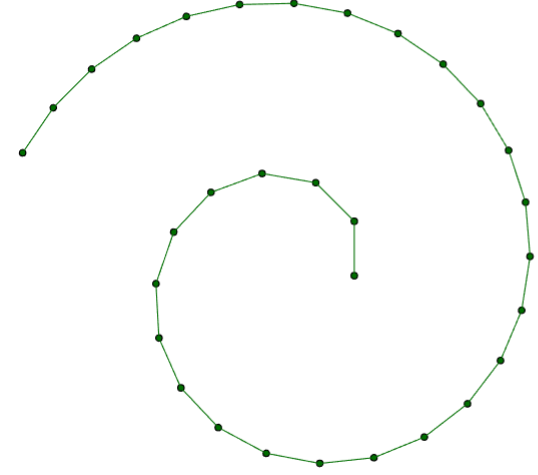
La concoide de Nicomedes es una curva plana ideada por el matemático griego Nicomedes, que vivió aproximadamente al mismo tiempo que Arquímedes en el siglo II a. C. El nombre de concoide, procedente de la palabra griega "κογχοειδής", hace referencia a que la forma de la curva recuerda al perfil de una concha. Es un tipo de concoide cuyos radios vectores trazados desde un punto fijo cortan a una recta (denominada "base") a una distancia constante. René Descartes incluyó en su obra "La Géométrie" (La Geometría) un método que permite dibujar la normal y, por lo tanto, la tangente de la concoide de Nicomedes .
El 14 de junio de 2016, Ildefonso publica la construcción dinámica de la Concoide de Nicomedes, que presentamos a continuación.
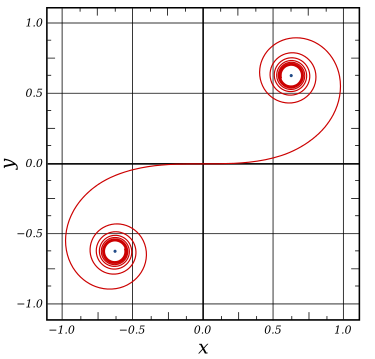
La clotoide, también denominada radioide de arcos o espiral de Cornú en honor de Marie Alfred Cornu, es una curva tangente al eje de las abscisas en el origen y cuyo radio de curvatura disminuye de manera inversamente proporcional a la distancia recorrida sobre ella. Es por ello que en el punto origen de la curva, el radio es infinito.
La expresión matemática usual es: $\displaystyle\;\rho\cdot s = C^2$
siendo: $\displaystyle\;\rho$ el radio de curvatura, $\displaystyle\; s$ el desarrollo o arco, y $\displaystyle\; C$ la constante de la espiral (Wikiwand).
El 11 de septiembre de 2016, Ildefonso publica la construcción de la espiral de Cornu con el objetivo de analizar las aproximaciones de las integrales de Fresnel mediante polinomios. Esta construcción la presentamos a continuación.
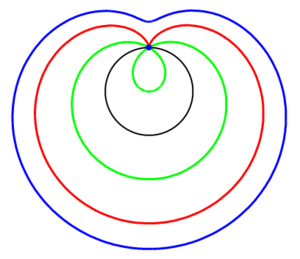
El caracol o «limaçon» de Pascal es la concoide de una circunferencia que pasa por el polo. Es un tipo de epitrocoide. La investigación formal más temprana en limaçons se atribuye generalmente a Étienne Pascal, padre de Blaise Pascal. Sin embargo, el artista renacentista alemán Alberto Durero ya había realizado anteriormente algunas investigaciones y su obra Underweysung der Messung (Instrucción de medición) tiene métodos geométricos específicos para la producción de limaçons. La curva fue nombrada por Gilles de Roberval cuando la utilizaba como un ejemplo para la búsqueda de líneas tangentes (Wikiwand).
Entre el 19 de noviembre y el 8 de diciembre de 2016, Ildefonso publica tres escenas acerca del Caracol de Pascal, que presentamos a continuación.
|
|
|
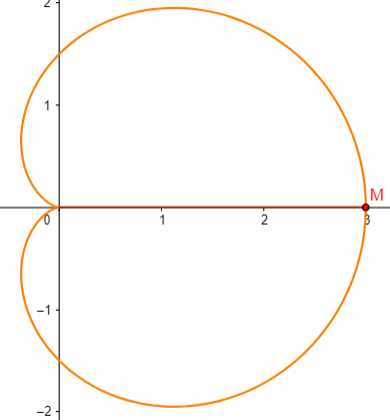
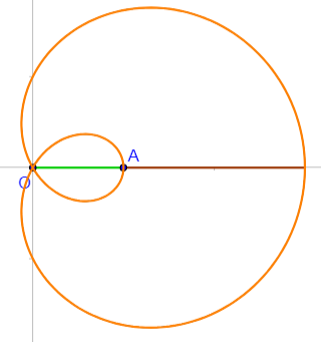
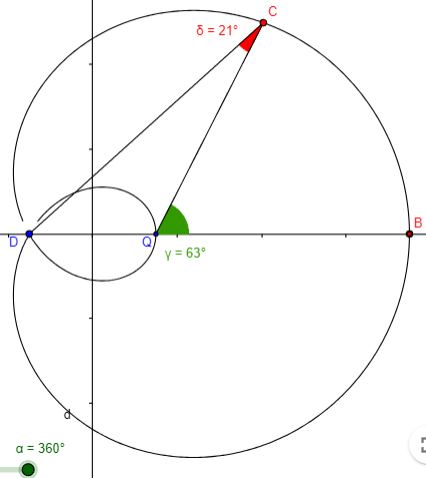
En la escena de la izquierda, se hace uso de la ecuación polar del Caracol de Pascal para su representación Gráfica
La escena del medio, presenta las ecuaciones del lugar geométrico "Caracol de Pascal", además de diferentes maneras de enfocar el estudio de este lugar geométrico.
La escena de la derecha, presenta el caracol de Pascal y su lazo interior, que para ciertos valores de los parámetros (a=b), pueden usarse como un trisector de ángulos.
En geometría, la trisectriz de Maclaurin es una curva cúbica notable por su propiedad de trisectriz, lo cual quiere decir que se puede usar para trisecar un ángulo. Se puede definir como el lugar geométrico de los puntos de intersección de dos rectas, girando cada una a una velocidad angular uniforme alrededor de puntos separados, de forma que la proporción de las velocidades de rotación sea de 1:3 y las líneas inicialmente coincidan con la línea entre los dos puntos.
Una generalización de esta construcción se denomina una sectriu de Maclaurin. La curva se denomina en honor al matemático escocés Colin Maclaurin, quien investigó la curva en 1742 (wikiwand).
En su página en GeoGebra, Ildefonso nos ofrece una escena interactiva, en la cual podemos mover el punto $A$ sobre la curva de Maclaurin y verificar que $\displaystyle\beta = \frac{\alpha}{3}$ (Ibid.).
La escena la puedes ver, haciendo clic sobre la siguiente imagen.
Fecha de publicación: 24 de diciembre de 2016
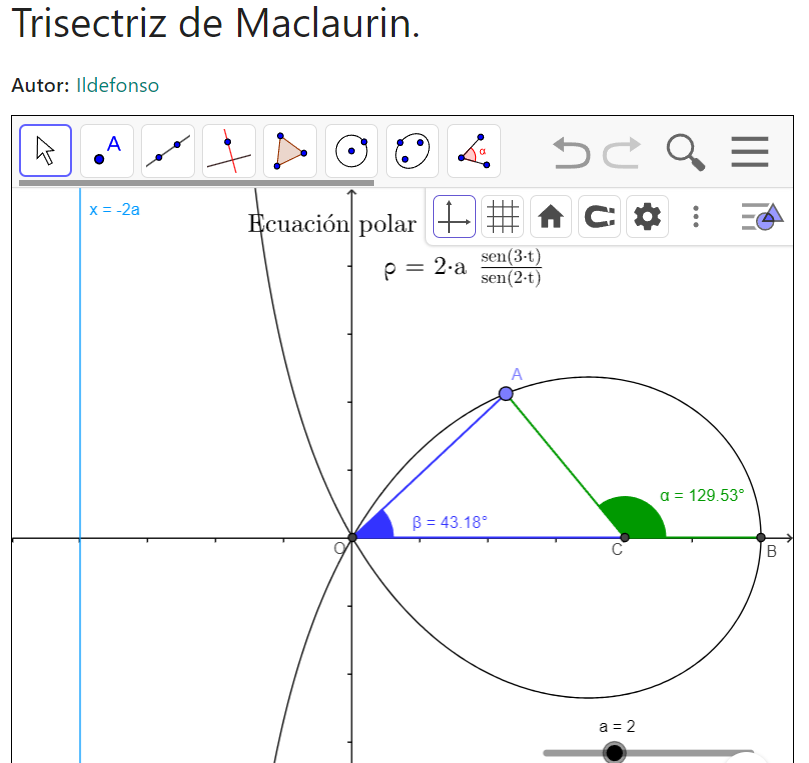
¡Haz clic sobre la imagen!
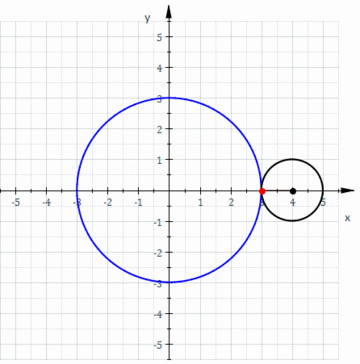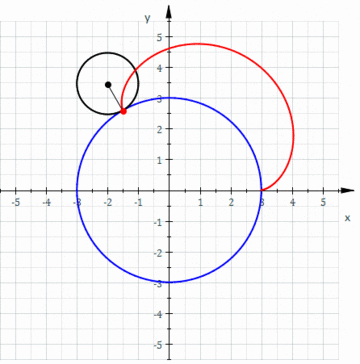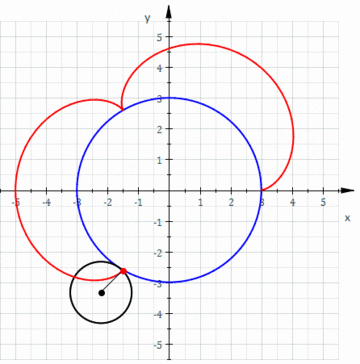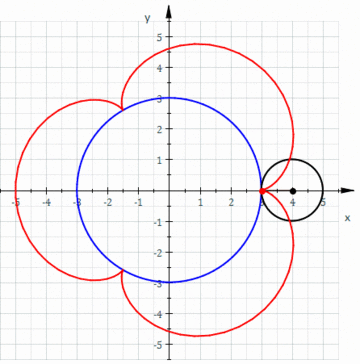
La epicicloide es la curva generada por la trayectoria de un punto perteneciente a una circun- ferencia (generatriz) que rueda, sin deslizamiento, por el exterior de otra circunferencia (directriz), es un tipo de ruleta cicloidalUna ruleta o curva cíclica se denomina a la curva plana que describe la trayectoria de un punto, vinculado a una curva generatriz $C_1$, que rueda sobre otra curva directriz $C_2$, tangencialmente, sin deslizamiento. Si la curva generatriz $C_1$ (la que rueda) es una circunferencia, se denomina ruleta cicloidal (Wikiwand).. En la animación de la derecha, la curva roja es una epicicloide trazada a medida que el pequeño círculo (radio r = 1) gira sobre la circunferencia de un círculo mayor de radio R = 3.
El 14 de enero de 2017, Ildefonso publica la siguiente escena, cuyo objetivo de este trabajo es servir de plantilla para el estudio de las Epicicloides (Wikiwand).
Arbelos (en griego ἄρβελος "cuchillo de zapatero") es una figura geométrica plana. Para dibujarla, se toman tres puntos A, B y C sobre la misma recta, y se construyen tres semicírculos con diámetros AB, BC y AC, ubicados en el mismo lado de la recta. A la figura limitada por estos semicírculos, se le llama arbelos.
La referencia más antigua conocida a esta figura se encuentra en el Libro de los Lemas (atribuido a Arquímedes por el geómetra árabe Thábit ibn Qurra), donde algunas de sus propiedades matemáticas se expresan como las Propuestas 4 a 8 (Wikiwand).
Entre el 17 y 19 de junio de 2018, Ildefonso muestra un gran interés por esta figura, llegando a publicar 12 escenas, de las cuales presentamos cuatro a continuación.
|
|
|
|
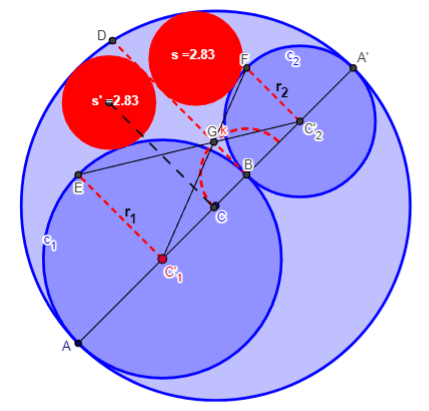
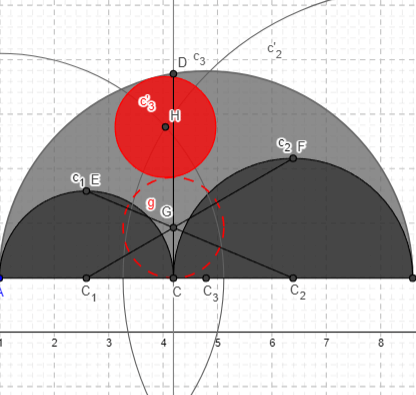
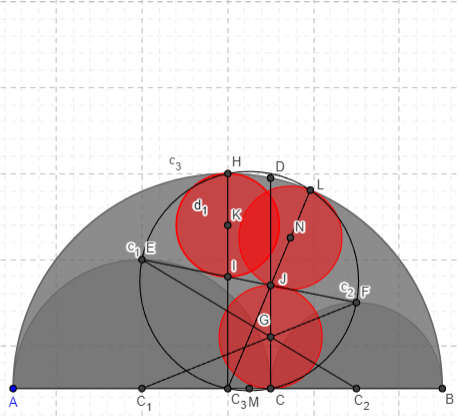
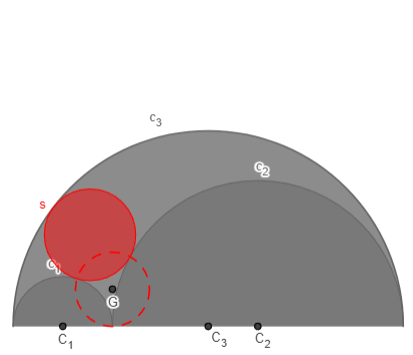
¡Haz clic sobre las imágenes!
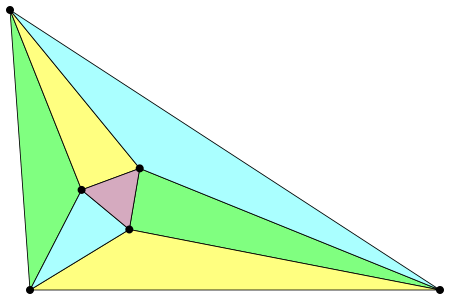
En geometría plana, el teorema de Morley establece que, en un triángulo cualquiera, los tres puntos de intersección entre trisectrices de ángulos adyacentes forman un triángulo equilátero, denominado triángulo de Morley. El teorema fue descubierto en 1889 por el matemático anglo- estadounidense Frank Morley. Tiene varias generalizaciones, en particular, si se intersecan todas las trisectrices, se obtienen otros cuatro triángulos equiláteros.
Cabe notar que, como no se puede trisecar un ángulo sólo con regla y compás, no se puede construir el triángulo de Morley con dichas limitaciones. Además, el teorema de Morley no se cumple en las geometrías esférica e hiperbólica (Wikiwand).
El 20 de junio de 2018, Ildefonso publica el triángulo de Morley, que presentamos a continuación.
Mueve los puntos $A, B$ o $C$
Entre el 20 y 22 de junio de 2018, Ildefonso publica 12 escenas dedicadas a los arcos, de las cuales presentamos cuatro.
|
|
|
|
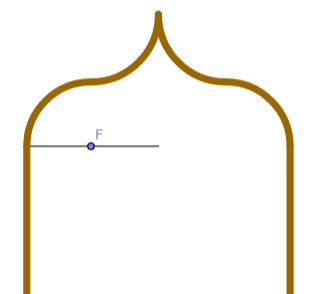
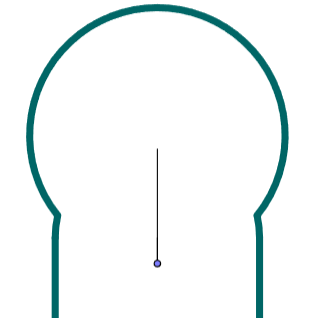
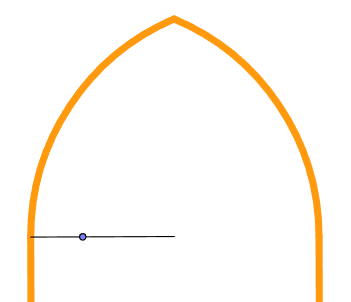
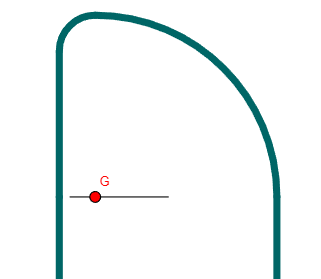
¡Haz clic sobre las imágenes!
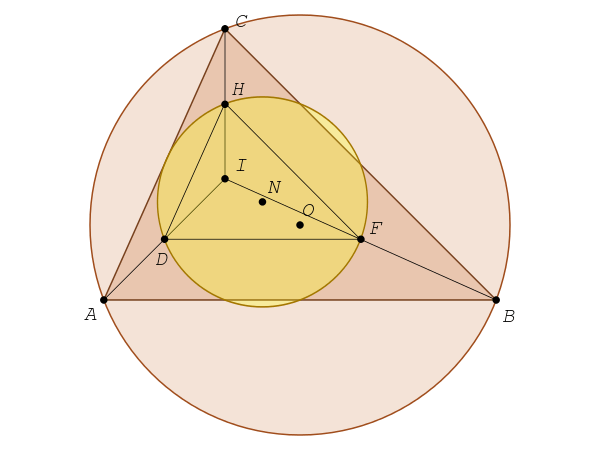
En geometría, se conoce como circunferencia de los nueve puntos aquella que se puede construir con puntos vinculados a cualquier triángulo propuesto. Su nombre deriva del hecho que la circunferencia pasa por nueve puntos notables, seis de ellos sobre el mismo triángulo (salvo que el triángulo sea obtusángulo aunque también existen). Generalmente, se adjudica al alemán Karl Wilhelm Feuerbach el descubrimiento de la circunferencia de los nueve puntos; sin embargo, lo que él descubrió fue la circunferencia de los seis puntos, reconociendo que sobre ella se encontraban los puntos medios de los lados de un triángulo y los pies de las alturas (en la figura, los puntos: M N P y E G J). (Wikiwand).
El 27 de junio de 2018, Ildefonso publica esta circunferencia, que presentamos a continuación.
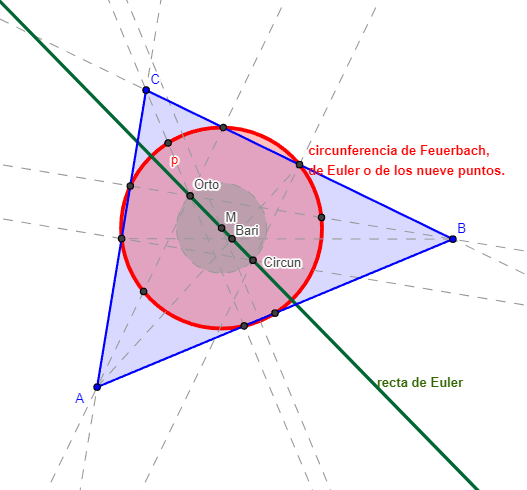
Haz clic sobre la imagen
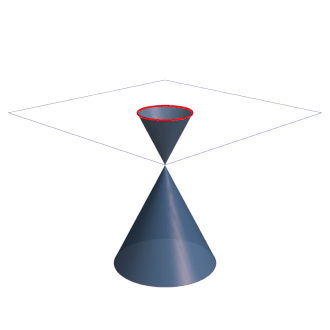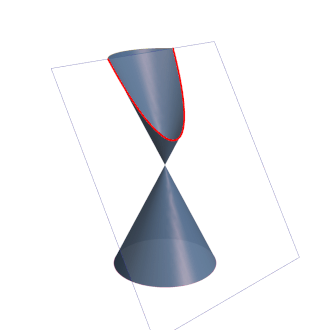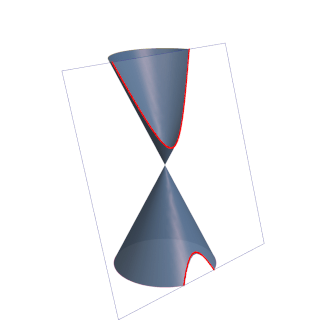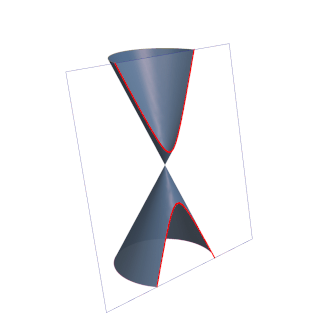
Se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas elipse, parábola, hipérbola y circunferencia. Una de las propiedades que define una cónica no circular es el conjunto de aquellos puntos cuyas distancias a algún punto en particular, llamado foco, y a alguna línea en particular, llamada directriz, están en una proporción fija, llamada excentricidad. El tipo de cónica viene determinado por el valor de la excentricidad (Wikiwand).
Entre el 2 y el 5 de julio de 2018, Ildefonso publica 10 escenas de cónicas, de las cuales presentamos cuatro.
|
|
|
|
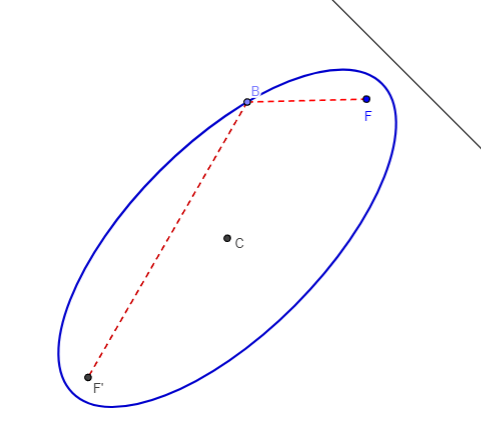
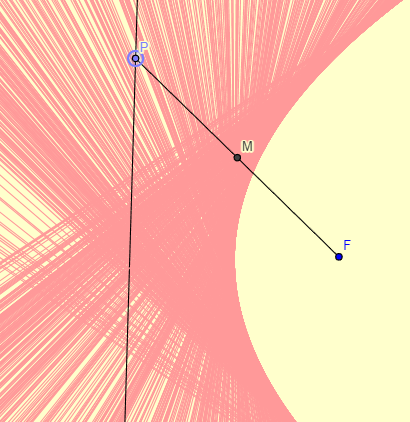
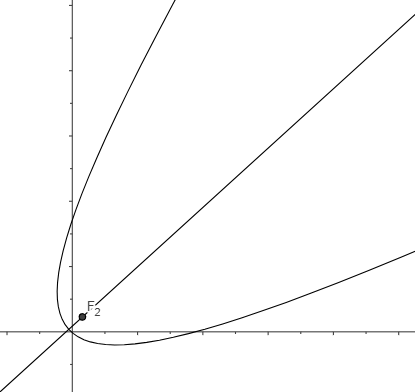
El tangram es un juego chino muy antiguo, que consiste en formar siluetas de figuras con las siete piezas dadas sin solaparlas. Las 7 piezas, llamadas "Tans", son las siguientes: 5 triángulos, dos construidos con la diagonal principal del mismo tamaño, los dos pequeños de la franja central también son del mismo tamaño y uno de tamaño medio ubicado en una esquina; un cuadrado y un paralelogramo. Normalmente los "Tans" se guardan formando un cuadrado. Una versión famosa es "grama" que significa escrito o gráfico. Otra versión dice que el origen del juego se remonta a los años 618 a 907 de nuestra era, época en la que reinó en China la dinastía Tang de donde se derivaría su nombre. (Wikiwand).
Esta fue una de las primeras escenas de Ildefonso, publicada en 2012, que luego incluye en el libro de GeoGebra "Geometría y razones".
La cuadratura de un polígono o la cuadratura de figuras lineales es una tarea que forma parte de las cuestiones estudiadas por la geometría clásica. Consiste en utilizar las herramientas euclidianas (regla y compás) para dibujar un cuadrado con un área del mismo tamaño que un polígono convexo o cóncavo dado. Johann Friedrich Lorenz describe en su libro Euklids Elemente, del año 1781, la solución de esta cuadratura "A partir de una figura rectilínea dada A, determinar un cuadrado de igual área". Los siguientes teoremas matemáticos de Euclides se utilizan para abordar la tarea (Wikipedia):
Esta escena fue la última publicación de Ildefonso en su página de GeoGebra (16 de diciembre de 2019).
Imagen de portada del capítulo: Ildefonso y otros autores.
Imagen de esta página: Torre, cimborrio y cúpulas de la catedral de Teruel (Turol Jones, CC BY 2.0).
Una de las tareas dispendiosas de la organización no gubernamental "Red Educativa Digital Descartes", fue recoger los materiales diseñados en Java y adaptarlos a JavaScript. Esta titánica tarea se inició en el mismo año que se crea la Red (2013), y continuó hasta el año 2015.
Eran muchos los materiales a adaptar y pocos los colaboradores, por lo que la carga de trabajo era más pesada. El 21 de octubre de 2013, Ángel Cabezudo informaba:
... con fecha de hoy tenemos publicados 361 títulos de Canals (96%) y 8 Misceláneas... A punto de finalizar esta primera fase y quedando un colaborador libre me propongo establecer las asignaciones y normas correspondientes de los siguientes materiales adaptados a JS y disponibles en la Web 1.0... ASIPISA Actualmente hay 30 objetos en la Web 1.0 y quedan pendientes de adaptar otros 8 que están ahora de la mano de Ildefonso Fernández Trujillo.
Ese mismo día, José Galo anota:
Muchas gracias por vuestras aportaciones y puntualizaciones. Enhorabuena Ángel y a tu equipo porque habéis cubierto rápidamente la producción actual. Comento algo: Las unidades de PISA de Ildefonso tienen particularidades adicionales a las de ASIPISA pues contemplan ¡evaluación formativa! por tanto rompe un poco en el esquema de ASIPISA y el formato. Por ello estimo que es conveniente publicarlas en miscelánea en el momento que Ildefonso termine de revisarlas y convertirlas a DescartesJS. Si el equipo se queda "ocioso" podemos planificar y distribuir misceláneas para convertirlas ¿no te parece Ángel?
Reitero mi enhorabuena y felicitación a todos. ¡Sois cartesianos hasta la médula! y personas de gran valía.
Lo de tarea titánica se comprende mejor al saber que eran miles de escenas interactivas a adaptar; por ejemplo, Ángel informaba sobre 361 títulos de Canals, cada título con cuatro escenas interactivas y Canals era sólo uno de los proyectos a adaptar. Pero, a la cantidad se sumaba la complejidad. El 8 de enero de 2014, Ildefonso envía el siguiente correo:
Hola. Feliz año 2014. He estado adaptando la unidad del transportador gráfico de Consolación Ruíz Gíl, que tiene una macro que hace girar el transportador según los valores de un contador con interfaz de barra. La macro contiene todos los elementos gráficos del transportador: texto, segmentos, puntos y arcos. Cuando el transportador gira para medir un ángulo todos sus componentes giran adecuadamente menos los arcos. He resuelto la adaptación sacando los arcos de la macro y creándolos en el espacio general adaptándolos al contador, pero lo suyo sería que pudieran permanecer en la macro. ¿Alguien puede ayudarme con esto? Gracias por vuestra atención. Saludos.
El problema de la escena con el transportador, es solucionado meses más tarde. Pero, los problemas unieron más a los miembros de la Red. Una continua comunicación, no por WhatsApp sino por correo, permitía que aprendiéramos unos de otros... ¡había mucho que aprender! Nos animamos, incluso, a diseñar y desarrollar talleres que enriquecieran nuestros conocimientos, para mejorar nuestros contenidos digitales puestos al servicio de la aldea global. En uno de esos talleres, el 19 de mayo de 2014, Ildefonso se presenta:
Hola. Mi nombre es Ildefonso Fernández Trujillo y soy profesor de Matemáticas de enseñanza media, ya jubilado. En la actualidad colaboro con el proyecto Descartes adaptando materiales propios y de otras compañeras y compañeros, y creando vídeos y artículos para el Blog del proyecto Descartes.
He visto el vídeo de presentación y ya he comenzado a conocer cosas nuevas y a intuir nuevas posibilidades de aplicación en la práctica docente, así que entro en el taller con el mismo interés con que entré en el taller de puzles y con la garantía de no quedar defraudado gracias al tallerista que lo dirige, a quien sigo y admiro, por su ingente y buen quehacer, desde hace ya varios años.
Un saludo cordial. Ildefonso Fernández Trujillo.
Del taller de puzles, que indica Ildefonso, presentamos una de sus tareas, en el que se destacan imágenes de Madrid y Móstoles, sus lugares de residencia y de trabajo.
Ildefonso adapta dos unidades didácticas, una de ellas con 11 escenas interactivas (en 2015) y la otra con 30 (en 2017).
Esta unidad, diseñada por Antolina Muñoz Huertas y adaptada por Ildefonso, se trata el concepto de proporcionalidad en su vertiente geométrica. En la introducción, Antolina destaca:
Uno de los siete sabios de Grecia, Thales de Mileto, habiendo oído hablar de la sabiduría de los egipcios monta en una nave y se dirige al Nilo. Estando en el desierto, un sacerdote le pregunta cuál será la altura de la pirámide del rey Khufú (pirámide de Keops). Thales se tumba en la arena y determina la longitud de su propio cuerpo. El sacerdote atónito le pregunta qué hace y él le contesta: "Me pondré en un extremo de la línea que marca mi cuerpo en la arena hasta que mi sombra sea igual de larga. En ese instante, la sombra de la pirámide, medirá tantos pasos como la altura de ésta.".
Esta es la primera idea de proporcionalidad geométrica.
Pocos conceptos han influido tanto a lo largo de las creaciones artísticas como la que conocemos como Proporción de Oro, y que Luca Pacioli, allá por el año 1500 y en pleno renacimiento italiano, identifica con el nombre de la Divina Proporción.
En la siguiente página, haz clic sobre la imagen para acceder a la unidad didáctica. En la parte inferior, hemos puesto la espiral de Fibonacci, adaptada al editor actual de DescartesLas espirales fueron de mucho interés para Ildefonso..
Esta unidad es diseñada por Antonio Caro Merchante y adaptada por Ildefonso. Parte de introducción a la unidad, es la siguiente:
Se llaman curvas cónicas a todas aquellas que se obtienen cortando un cono con un plano. Debido a su origen las curvas cónicas se llaman a veces secciones cónicas.
El matemático griego Menecmo (350 A.C.) descubrió estas curvas y fue el matemático griego Apolonio (262-190 A.C.) de Perga el primero en estudiar detalladamente las curvas cónicas y encontrar la propiedad plana que las definía. Apolonio descubrió que las cónicas se podían clasificar en tres tipos a los que dio el nombre de: elipses, hipérbolas y parábolas.
Quizás las propiedades más interesantes y útiles que descubrió Apolonio de las cónicas son las llamadas propiedades de reflexión. Si se construyen espejos con la forma de una curva cónica que gira alrededor de su eje, se obtienen los llamados espejos elípticos, parabólicos o hiperbólicos. Apolonio demostró que si se coloca una fuente de luz en el foco de un espejo elíptico, entonces la luz reflejada en el espejo se concentra en el otro foco. Si se recibe luz de una fuente lejana con un espejo parabólico de manera que los rayos incidentes son paralelos al eje del espejo, entonces la luz reflejada por el espejo se concentra en el foco. Esta propiedad permite encender un papel si se coloca en el foco de un espejo parabólico y el eje del espejo se apunta hacia el Sol. Existe la leyenda de que Arquímedes (287-212 A.C.) logró incendiar las naves romanas durante la defensa de Siracusa usando las propiedades de los espejos parabólicos. En la actualidad esta propiedad se utiliza para los radares, las antenas de televisión y espejos solares. La propiedad análoga, que nos dice que un rayo que parte del foco se refleja paralelamente al eje sirve para que los faros de los automóviles concentren el haz en la dirección de la carretera o para estufas. En el caso de los espejos hiperbólicos, la luz proveniente de uno de los focos se refleja como si viniera del otro foco, esta propiedad se utiliza en los grandes estadios para conseguir una superficie mayor iluminada.
En el siglo XVI el filósofo y matemático René Descartes (1596-1650) desarrolló un método para relacionar las curvas con ecuaciones. Este método es la llamada Geometría Analítica. En la Geometría Analítica las curvas cónicas se pueden representar por ecuaciones de segundo grado en las variables x e y. El resultado más sorprendente de la Geometría Analítica es que todas las ecuaciones de segundo grado en dos variables representan secciones cónicas y se lo debemos a Jan de Witt (1629-1672).
Haz clic sobre la siguiente imagen, para acceder a la unidad didáctica:
Del Proyecto Misceláneas, Ildefonso adapta 26 de ellas.
Miscelánea adaptada por Ildefonso en 2014. En el juego se trata de adivinar un número comprendido entre 1 y 1000 en diez intentos, o menos. Para acceder a la miscelánea, haz clic en este enlace o interactúa, a continuación, con el juego.
En la siguiente página, presentamos la miscelánea.
Ildefonso adapta esta miscelánea en 2014, en la que se puede practicar el cálculo de áreas de recintos limitados por dos curvas. Haz clic en la siguiente imagen, para acceder al recurso:
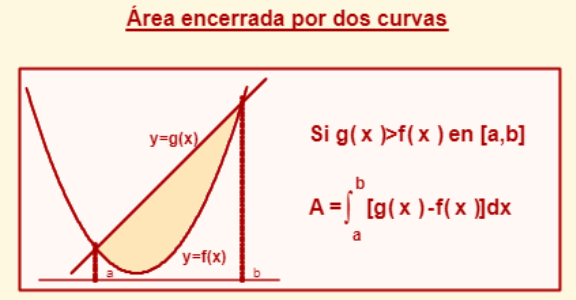
Miscelánea adaptada por Ildefonso en 2015, en la que se puede practicar los conceptos de: gráfica de una función definida a trozos, continuidad de una función en un punto, límites laterales y límite.
Miscelánea adaptada por Ildefonso en 2014, en la que se pueden realizar ejercicios de cálculo de áreas y perímetros de polígonos
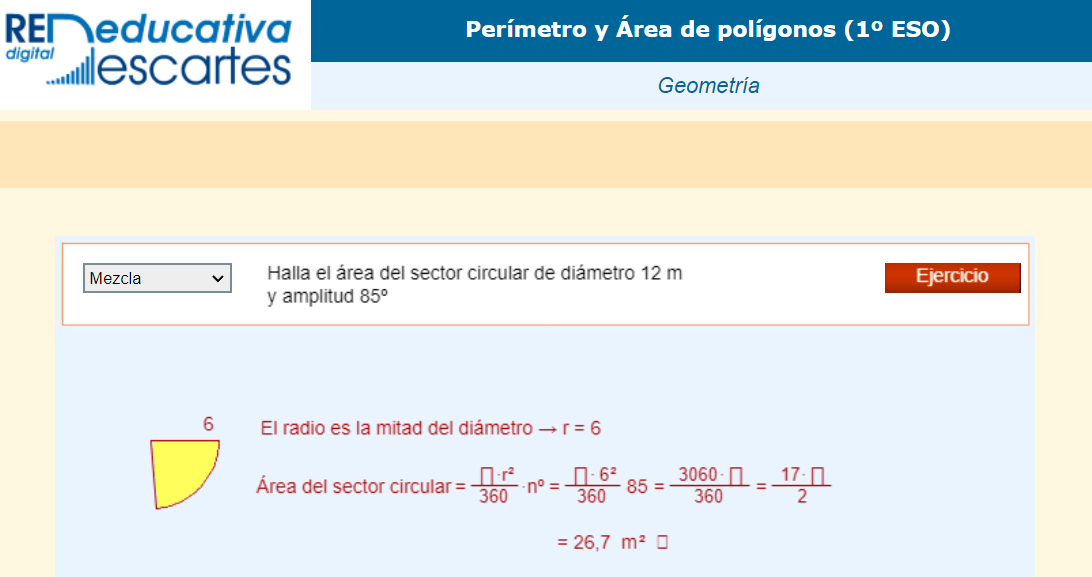
Adaptada por Ildefonso en 2014. Haz clic en la siguiente imagen, para acceder al recurso:
Adaptada por Ildefonso en 2014. Haz clic en la siguiente imagen, para acceder al recurso:
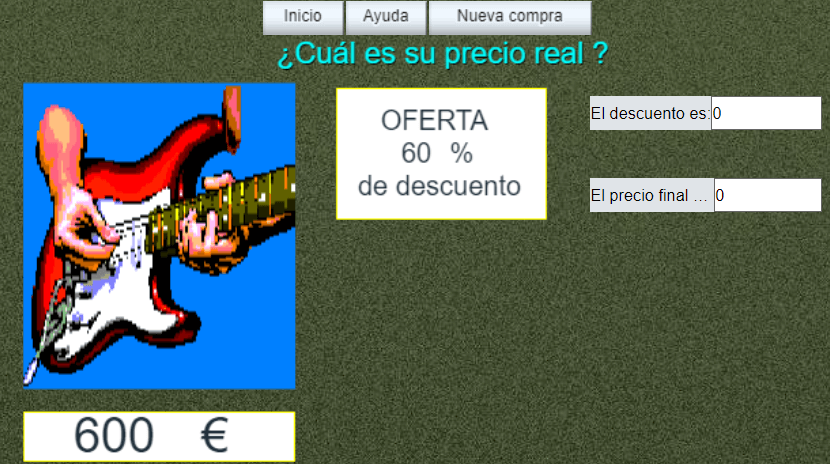
Adaptada por Ildefonso en 2013. Haz clic en la siguiente imagen, para acceder al recurso:
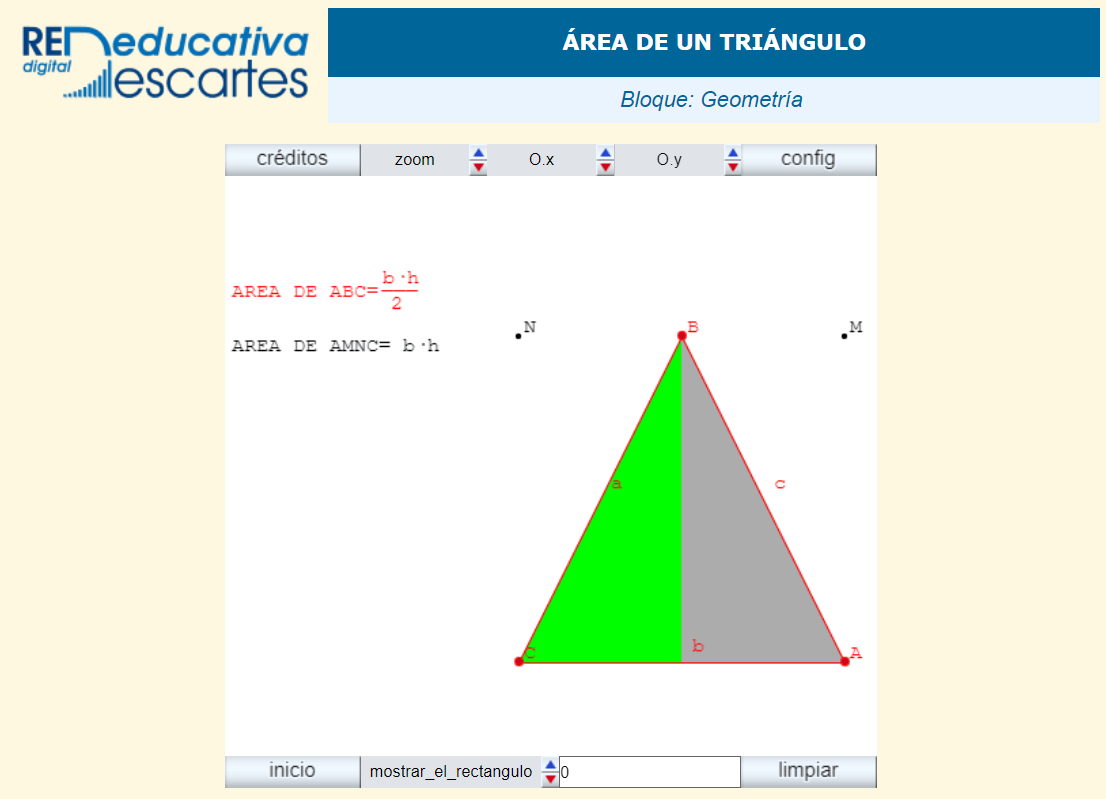
Adaptada por Ildefonso y Ángel Cabezudo Bueno en 2014. Puedes acceder al recurso haciendo clic en este enlace, o interactuar en esta escenaA partir de un polígono regular convexo de N lados se puede obtener un polígono estrellado. Para ello se unen los vértices no consecutivos, según un salto establecido de M vértices, de tal forma que se recorran todos los vértices del polígono.:
Esta miscelánea, diseñada por Consolación Ruiz Gil, la adaptan Ildefonso y Ángel Cabezudo en 2015. La escena nos permite ver las coordenadas de un punto en una base cualquiera de $\Reals^3$, se puede practicar con los conceptos de: Representación gráfica del espacio de tres dimensiones, semejanza y escala, coordenadas tridimensionales y visión espacial. Con el color se distingue la orientación de la base. Haz clic en la siguiente imagen, para acceder al recurso:
En la siguiente página, hemos puesto la escena en la que debes introducir valores en cada cuadro de texto, observando la reacción del programa.
Ildefonso y Ángel Cabezudo adaptan esta miscelánea en 2015. Haz clic en la siguiente imagen, para acceder al recurso:
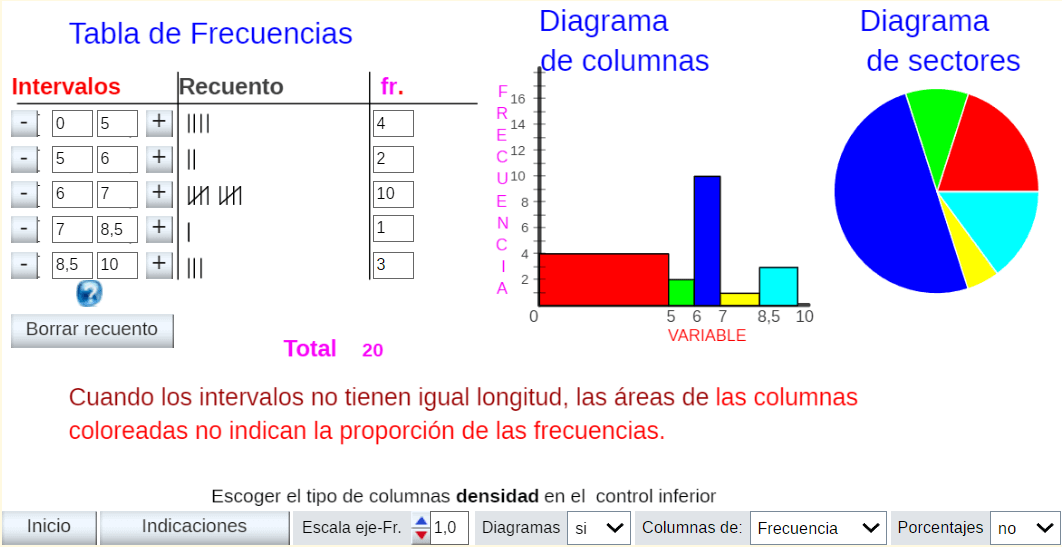
Miscelánea adaptada por Ildefonso en 2014, en la que al disponer ordenadamente los números en una tabla se pueden observar ciertas regularidades que permiten realizar divisiones, obtener divisores, calcular múltiplos, etc..
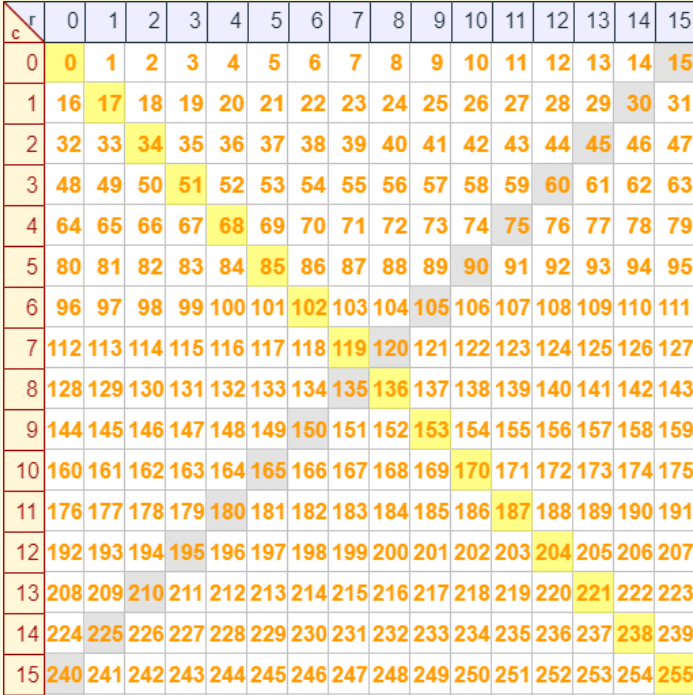
Miscelánea adaptada por Ildefonso en 2014, en la que mediante el método de arrastrar y soltar se colocan cada uno de los triángulos de la izquierda en la franja que le corresponde en la parte derecha de la nueva pantalla.
Puedes acceder al recurso haciendo clic en este enlace, o practicar en la siguiente escena:
Ildefonso adapta esta miscelánea en 2014. Se busca hallar la ecuación vectorial de la recta determinada por dos planos o la ecuación vectorial de un plano. Haz clic en la imagen de la derecha, para acceder al recurso:
Miscelánea adaptada por Ildefonso en 2014 con escenas dinámicas e interactivas para reforzar la identificación de un triángulo según sus ángulos.
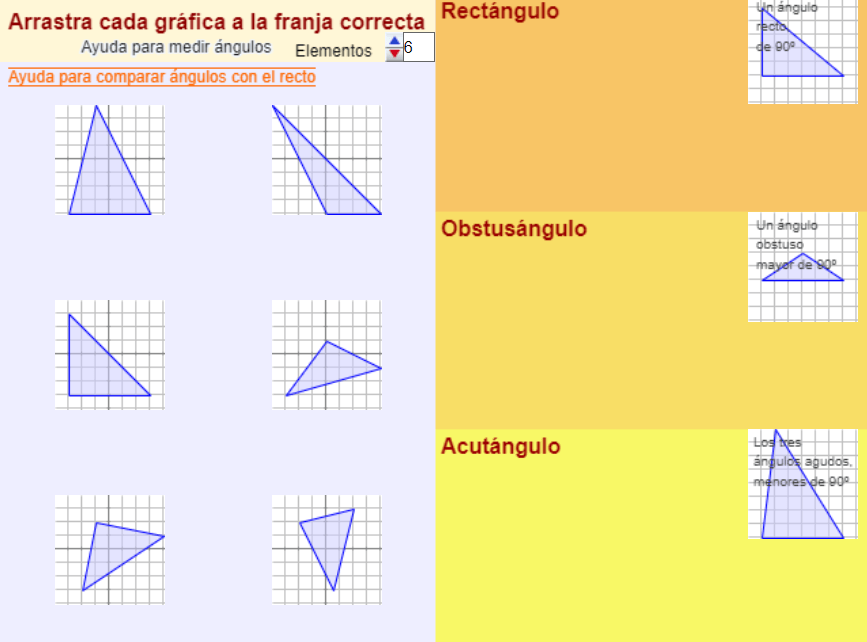
Ildefonso y Ángel Cabezudo adaptan esta miscelánea en 2015. Se muestra una foto del instituto José María Pereda. Siguiendo las indicaciones, podemos medir algunos de los recorridos, con ayuda de la regla y calcular la escala de la foto. Haz clic en la imagen de la izquierda, para acceder al recurso:
Miscelánea adaptada por Ildefonso y Ángel Cabezudo en 2015, en la que se debe medir la pendiente de la tangente a distintas curvas en algunos puntos para calcular el valor de la derivada en ellos.
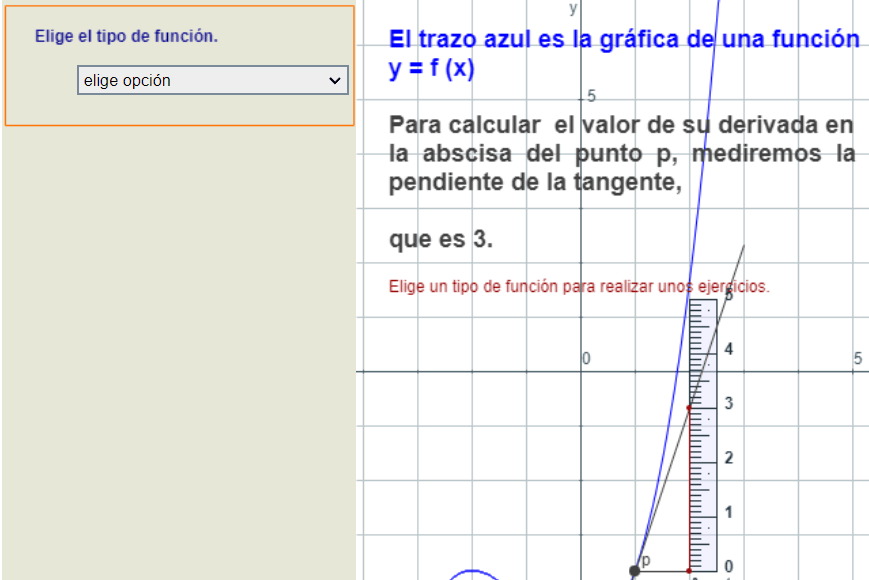
Adaptada por Ildefonso y Ángel Cabezudo Bueno en 2014, luego de haber solucionado el problema de la macro descrita en la introducción de este capítulo. Puedes acceder al recurso haciendo clic en este enlace, o interactuar en esta escena:
Ildefonso adapta esta miscelánea en 2013, en la que se construyen triángulos con ayuda del geoplano virtual; para ello, se mueven los puntos A, B, C, pinchando sobre ellos y arras- trando para conseguir el triángulo que indica el ejercicio. Incluye hoja de trabajo en formato PDF. Haz clic en la imagen de la derecha, para acceder al recurso:
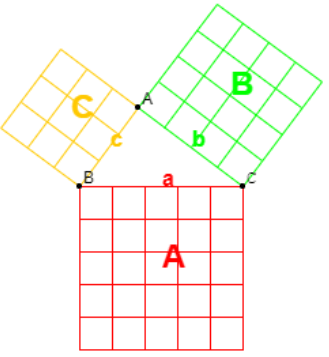
Miscelánea adaptada por en 2014 Ildefonso, en la que se clasifican triángulos, conocidos los lados y atendiendo a los ángulos, apoyada por diez ejercicios secuenciales y auto- explicativos. Incluye hoja de trabajo en formato PDF.
Ildefonso adapta esta miscelánea en 2013, en la que se calcula el IVA. Haz clic en la siguiente imagen, para acceder al recurso:
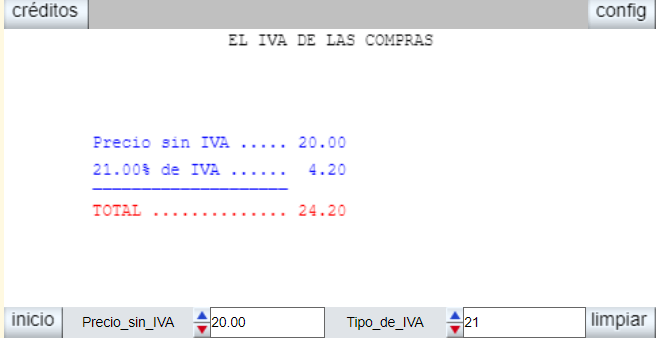
Miscelánea adaptada por Ildefonso en 2013, en la que se muestran, gráficamente, los cuadrados de números naturales.
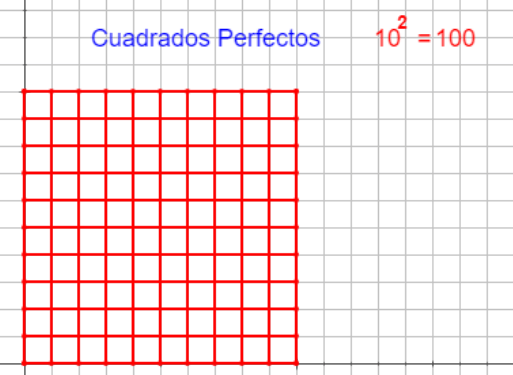
Adaptada por Ildefonso en 2017, en la escena se muestran unos parámetros que ajustan la posición y tamaño de la elipse. Mueve el punto rojo situado sobre la elipse y comprueba que en cualquier caso la suma de las distancias del punto a cada uno de los focos, F y G, siempre da 10. Puedes acceder al recurso haciendo clic en este enlace, o interactuar en esta escena:
Ildefonso adapta esta miscelánea en 2014, es una escena animada con DescartesJS. Haz clic en la siguiente imagen, para acceder al recurso:
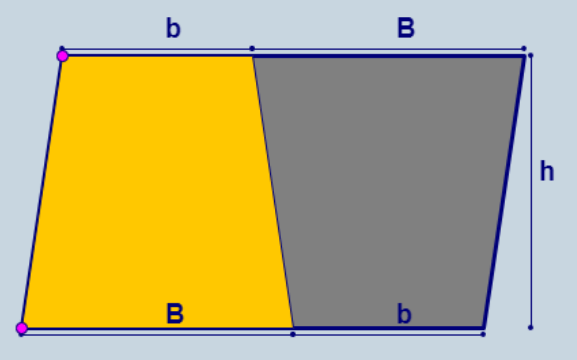
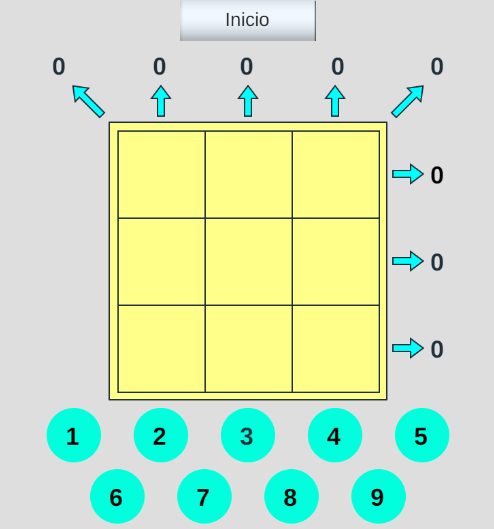
Miscelánea adaptada en 2014 por Ildefonso, en el que se debe rellenar las celdas del cuadrado, sin repetir número y de forma que la suma de las cifras de cada fila, de cada columna, de la diagonal principal y de la diagonal secundaria sea igual.
Ildefonso adapta esta miscelánea en 2014. Los autores, hacen la siguiente introducción: Cualquier vector $A$ del plano $\Reals\times\Reals$ se puede expresar, de forma única, como combinación lineal de otros dos $U$ y $V$ que tengan distinta dirección.
$$A = a\cdot U + b\cdot V$$
Dos vectores $U$ y $V$ no colineales constituyen una base de representación de los vectores del plano. Los coeficientes $a$ y $b$ reales por los que hay que multiplicar los vectores de la base $\lbrace U, V\rbrace$ son las coordenadas del vector $A$. Si cambia el vector $A$ en esa base o cambia la propia base $\lbrace U, V\rbrace$ cambiarán las coordenadas de $A$. La escena muestra esta situación facilitando la observación del cambio dinámico de los componentes y las coordenadas.
Haz clic en la siguiente imagen, para acceder al recurso:
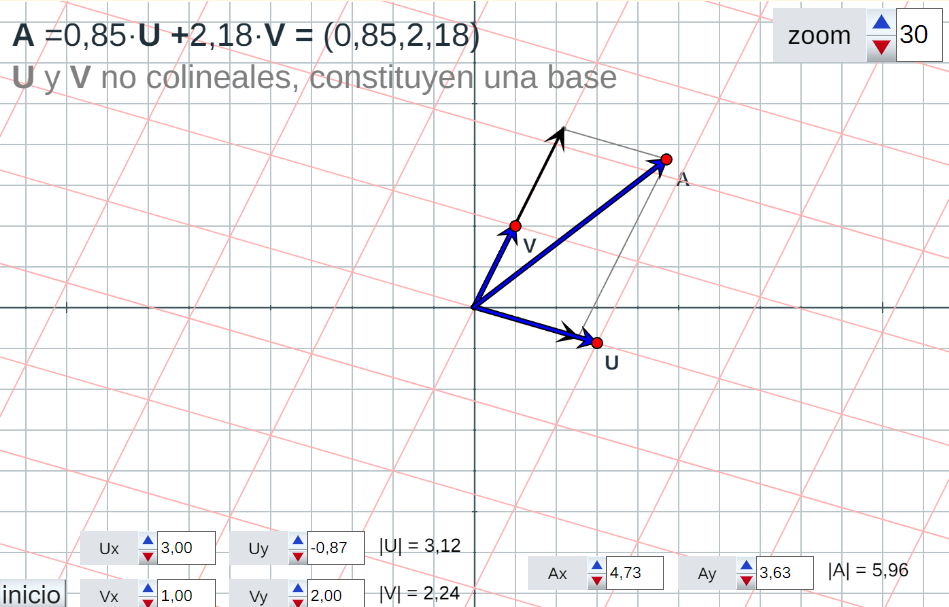
Torre mudéjar de la Iglesia de El Salvador, Teruel (Zarateman, CC0).
Una vez que se constituyó la organización no gubernamental "Red Educativa Digital Descartes" en junio de 2013 se comenzó a diseñar la web de la asociación. Inicialmente se elaboró una web 1.0 en la que se fueron publicando los recursos de los diferentes subproyectos del proyecto Descartes a medida que se iban convirtiendo a DescartesJS. Pero, paralelamente, se planificó ir desarrollando una web 2.0, un servidor de contenidos en el que se pudiera introducir cierta retroalimentación por parte de los usuarios y entre las secciones a incluir surgió un blog que sirviera como elemento divulgador de noticias de la asociación, de experiencias de aula, de vídeos explicativos o demostrativos o en los que se hablara o explicara con detalle el contenido de escenas o recursos en general.
Este blog lo coordinó y dirigió en sus primeros años nuestra socia Eva María Perdiguero Garzo y pasó a formar un equipo de colaboradores que se encargaran de diferentes temas e hicieran publicaciones periódicas de manera que hubiera movimiento y cambios en la portada de nuestro servidor, mostrando la vitalidad interna del proyecto. Idelfonso se incorporó como colaborador del blog y publicó su primer artículo el 30 de mayo de 2014.
Con posterioridad Eva, por circunstancias personales —ya hemos indicado que no es fácil compaginar el altruismo de nuestra RED con la vida laboral, familiar o personal—, tuvo que desconectarse de la primera línea de la asociación y pasó a coordinar el blog Ángel Cabezudo Bueno. Ildefonso siguió colaborando y publicó su último artículo el 10 de septiembre de 2022.
En el periodo del 30 de mayo de 2014 hasta el 28 de septiembre de 2018, Ildefonso publicó un total de cincuenta y dos artículos, uno cada mes. Y posteriormente publicó tres en el mes de septiembre de 2020, de 2021 y 2022 sobre la planificación didácTICa y de recursos de Bachillerato al inicio de cada curso escolar.
En los contenidos que incluía en cada artículo a menudo combinaba diferentes estrategias divulgadoras y, a veces, planteaba una mezcolanza de noticias de la asociación, de planteamientos de contenidos matemáticos apoyándose en recursos interactivos propios o ajenos, el detalle del código interno de las escenas de Descartes para enseñar a desarrollar con DescartesJS, muestras de trabajos personales elaborados en cursos internos de nuestra asociación y, en general, saberes que consideraba de interés personal y que eran dignos de compartir con los demás. Un totum revolutum en el que se puede encontrar numerosas sorpresas que, a veces, no son esperadas si nos ceñimos exclusivamente a lo indicado en el título del artículo.
Para poder integrar todos esos artículos en este libro es obvio que no podemos extendernos en su descripción, ni embeberlos directa-mente aquí, sería elevado el número de páginas que comprendería. Por ello, hemos optado por aportar al lector un breve resumen o guía del contenido y enlazarle extenarmente el artículo tal y como lo escribió él Puede que algún enlace de los que incluyera Ildefonso externo a nuestra web, ya no esté accesible. Es el precio que pagamos por la intrínseca dinámica de las web. , y como está actualmente en nuestro servidor de RED Descartes. Pulsando sobre cada imagen accederá al contenido del artículo.
26 de septiembre de 2014.
Ildefonso aborda la necesidad de seguir una adecuada estrategia para resolver problemas. Se ubica en el problema de construir un cuadrado mágico 3x3 y da pautas para lograr su resolución. Con ayuda de una escena interactiva invita al usuario a aplicar dicha estrategia.
Posteriormente aborda la extensión de esa estrategia a seguir con cuadrados 4x4 enlazando un vídeo explicativo que también nos puede ayudar a su ampliación a cuadrados mágicos de orden superior.
Finalmente aporta una hoja de cálculo con la que construir cuadrados mágicos hasta de orden 11.
También hace referencia a otra escena de Elena Álvarez que integra más de 400 comandos de acceso desde Descartes al cálculo simbólico de GeoGebra.
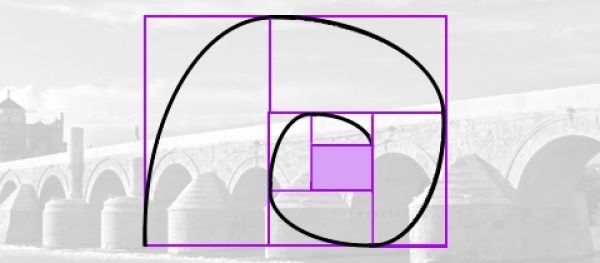26 de febrero de 2016.
Comunica el trabajo colaborativo de crear breves libros interactivos dentro del proyecto GEOgráfica y de un nuevo tipo de puzle con vídeos, es decir imágenes dinámicas en lugar de imágenes estáticas.
En la escena compendio de espirales incluye en esta ocasión la espiral gnomónica cordobesa o espiral generalizada de Durero cordobesa.
25 de marzo de 2016.
Ildefonso nos comunica nuevos recursos publicados en RED Descartes que en este caso se centran en la división del proyecto GEOgráfica en varias secciones para tener clasificados los ya numerosos objetos interactivos que se han desarrollado, junto a un taller de curvatura y nuevos cuadernos interactivos para el aprendizaje de los números enteros.
Finalmente integra la espiral de Durero en la escena compendio de espirales y de ella nos presenta el detalle de su construcción gnomónica.
En el bloque de espirales enlaza dos misceláneas. Una correspon-diente a la espiral de Arquímedes y otra a la logarítmica. Y para finalizar incorpora la espiral de Fibonacci a la escena de espirales.
Esta vez nos presenta la espiral hiperbólica y también la incorpora a la escena de espirales. Y continúa con una construcción en la que la trisección del ángulo se realiza usando la espiral de Arquímedes y otra que muestra de nuevo la cuadratura del círculo. Finalmente reitera las construcciones de trisección y cuadratura en GeoGebra.
22 de julio de 2016.
Los subproyectos TELEsecundaria, GEOevaluación y Plantillas son de nuevo referenciados e incluye un ejemplo del avance obtenido en cada uno de ellos.
Como lugar geométrico podemos observar la Concoide de Nicómedes.
La espiral que se incluye en este caso a la escena de espirales es la logarítmica.
En GeoGebra muestra también la Concoide y cómo puede usarse para la trisección de un ángulo.
25 de noviembre de 2016.
Se exponen varias escenas, en el estudio de los lugares geométricos y sus aplicaciones, que están relacionadas con el "Caracol de Pascal". La primera obtiene el caracol como la podaria de una circunferencia respecto a un punto, la segunda en base a la cuerda de una circunferencia y la tercera al rotar una circunferencia sobre otra sin deslizamiento entre ellas (cuando estas circunferencias son iguales se obtiene la cardiode).
En las construcciones de GeoGebra se ha incluido también el caracol de Pascal.
27 de enero de 2017.
En este artículo se describe y muestra la "Trisectriz de Maclaurin" y cómo el lazo de esa curva sirve también para la trisección de un ángulo.
Ambas escenas se desarrollan también en construcciones de GeoGebra.
Ildefonso invita a sus lectores a elaborar una miscelánea de Descartes que agrupe los lugares geométricos que se van estudiando, de manera análoga a lo realizado con la miscelánea de "Las espirales".
24 de marzo de 2017.
Se desarrolla una aproximación al conocimiento genérico de los lugares geométricos conocidos como "Epicicloides" e "Hipocicloides" que son un tipo de Epi/Hipo Trocoides que a su vez son una clase de las Ruletas.
Se adapta como plantilla de desarrollo de las escenas una procedente de los cartesianos mejicanos.
28 de abril de 2017.
La "Trisectriz (Cuadratriz) de Hipias" y la "Concoide (Trisectriz) de Nicomedes" son las curvas resultantes del trabajo de estos sabios griegos para resolver el problema de la trisección de un ángulo.
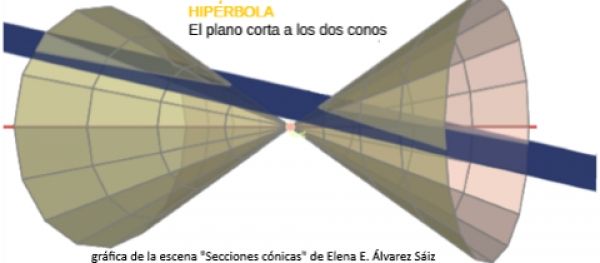
23 de junio de 2017.
En este artículo nos centramos en la hipérbola y observamos dos construcciones de la misma como lugar geométrico y otras realizadas con escenas desarrolladas con DescartesJS.
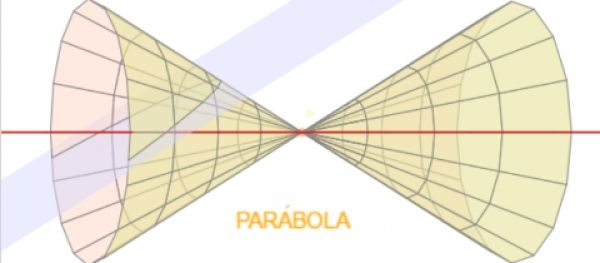
31 de julio de 2017.
Siguiendo con la serie de artículos sobre las cónicas nos adentramos en la parábola que de nuevo se analiza con escenas interactivas de Descartes y construcciones de GeoGebra.
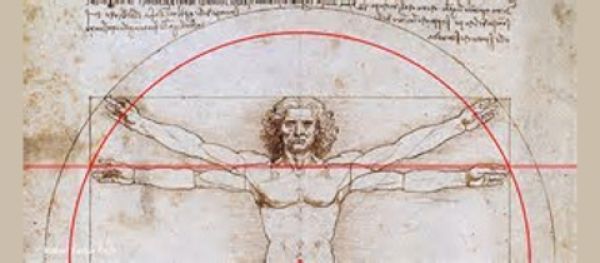
25 de agosto de 2017.
Inicia otra serie de artículos sobre cuadraturas. Continúa la aproximación al conocimiento genérico de los lugares geométricos analizando aspectos de las Cuadraturas y su relación con las teselaciones.
Comienza con la cuadratura de un octógono regular usando un metodo que es generalizable para todo polígono regular y un segundo método por descomposición en otros polígonos. También pone dos ejemplos de teselaciones.
26 de enero de 2018.
Con la ayuda de escenas que había desarrollado con anterioridad, Ildefonso aborda la cuadratura del círculo.
27 de febrero de 2018.
Ildefonso, en este artículo, hace un recorrido sobre las últimas escenas interactivas que se habían incorporado al subproyecto Misceláneas, de algunas de ellas es autor aunque no lo indica explícitamente.
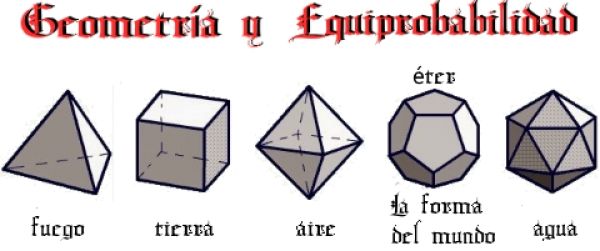22 de junio de 2018.
Se introduce la inferencia estadística referenciando recursos educativos desarrollados con Descartes.
Aborda el problema de la aguja de Buffon y enlaza una miscelánea codificada junto a Ángel Cabezudo.
Nota bene: A partir de este momento, Ildefonso deja su colaboración mensual y su intervención en el blog pasa a ser de una colaboración anual con motivo del inicio del curso escolar. Ya hemos reiterado que el altruismo de nuestra RED Descartes no siempre puede ser asumido y las circunstancias personales o familiares limitan en determinados momentos. No obstante, continuó participando en otras labores esporádicas que durante esos años fueron surgiendo.
1 de septiembre de 2020.
El contenido de este artículo es análogo al anterior, pero en la parte final se centra en las circunstancias que acontecieron en el último trimestre del curso anterior (cierre de aulas por la pandemia) y enlaza la experiencia de nuestro socio José Antonio Salgueiro.
16 de septiembre de 2021.
Ildefonso realiza pocos cambios al contenido del artículo anterior.
10 de septiembre de 2022.
Último artículo de Ildefonso en nuestro blog. En este caso incluye y referencia libros interactivos del proyecto iCartesiLibri junto a los contenidos tratados en los artículos anteriores.
Playa de la Renegà- Oropesa del Mar - Castellón - España.
Foto: Angel Cabezudo Bueno (2021) - COO
En capítulos anteriores ya han surgido referencias al Nautilus, al atractivo matemático de su concha y al interés que Ildefonso manifestó por su estudio y comprensión. Por ello, aun siendo conscientes de que hemos de evitar ser repetitivos, estimamos necesario dedicar un capítulo al estudio colaborativo que Ildefonso hizo con Ángel Cabezudo y José R. Galo y que quedó detallado y plasmado en el artículo "Sobre la forma y crecimiento cordobés del Nautilus pompilius" Épsilon - Revista de Educación Matemática 2016, Vol. 33 (3), nº 94, 81-110.
No siempre es fácil establecer el porqué, cuándo y cómo del inicio de un proyecto y, en este caso, cuáles fueron las motivaciones que condujeron a Ildefonso y a sus dos colegas a plantearse el estudio o análisis de la concha del Nautilus, pero es obvio que si estaban trabajando con la proporción cordobesa y con espirales gnomónicas —según hemos podido constatar en capítulos anteriores— es que ya habían acudido a la llamada de Aristóteles que estableció el concepto de crecimiento gnomónico cuando afirmó:
«Hay ciertas cosas que cuando crecen no sufren alteración salvo en magnitud»
Y definió el gnomon como
Toda figura cuya yuxtaposición a otra figura dada produce una figura resultante que es semejante a la inicial.
En la imagen animada de la puede observarse cómo crece gnomónicamente el Nautilus y también es obvia la aparente forma espiral que adopta en ese crecimiento, digamos aparente porque todo es apariencia mientras no se fundamente. Pero al menos desde 1838 ya tenemos referencias en las que se afirma el crecimiento del Nautilus siguiendo una espiral y en concreto una espiral logarítmica H. Moseley (1938). On the geometrical forms of turbinated and discoid shells, Phil. Trans. 1838, Pt. i, pp. 351-370. cuyo factor de crecimiento o pulsación radial La espiral logarítmica verifica que el cociente entre las longitudes de dos radios vectores que se diferencian en 2π radianes es constante —por ello se le denomina también como espiral geométrica—, este valor es la denominada pulsación radial o factor de crecimiento. es 3. También se detalla en el bien conocido libro de D'Arcy Thompson Thompson, D. (1917). On Growth and Form. Cambridge University Press. indicando que su ángulo característicoLa espiral logarítmica también se denomina equiangular porque en cualquier punto de ella el ángulo que forma la recta tangente con el radio vector es constante. Este ángulo se denomina ángulo característico de la espiral. es de 80º 5’.
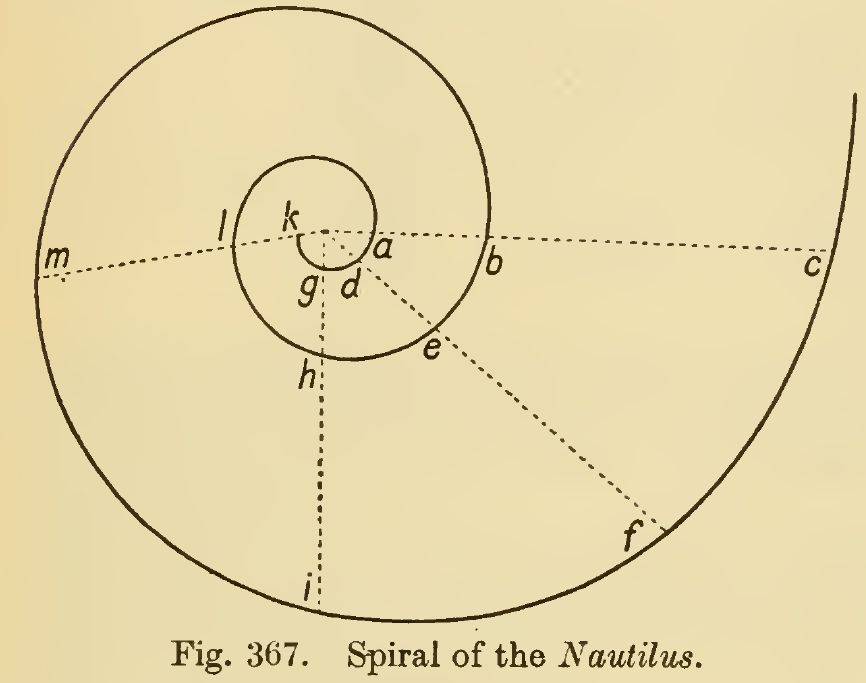
Así pues, no es de extrañar, que al igual que otros muchos más lo han hecho con anterioridad, Ildefonso, Ángel y José procedieran a cotejar el crecimiento del Nautilus. Pero a diferencia de la medida que pudo realizar Moseley (ver la ) que fueron medidas locales de radios vectores que están ligadas y son dependientes de la fijación previa del polo de la espiral buscada y, por tanto, con una imprecisión que se traslada a todo el estudio, tal y como lo señala Thompson (1945, p. 771), ellos disponían de la herramienta Descartes con la que podían abordar un contraste global consistente en dibujar sobre la sección de la concha del Nautilus una espiral logarítmica a la que podían variar su factor de crecimiento y cambiar la ubicación de su polo y de esta manera comprobar cuál de todas ellas se ajustaba mejor (interactuar con el ). Una comparativa global dado que se están ajustando todos los puntos de la espiral a la vez.
Con esa escena interactiva de Descartes el ajuste fue sencillo —en todo trabajo la disponibilidad de una herramienta adecuada es fundamental— y la espiral logarítmica hallada era aproximadamente Para que la expresión de la espiral obtenida fuese la más simple posible se ubicó la imagen del Nautilus de manera que el polo fuese $(0, 0)$ y se escaló esa imagen para que el factor de escala de la espiral obtenida fuese 1. En general la ecuación de una espiral logarítmica de polo $(0,0)$ es $r=a b^\theta=b^{\theta_0+\theta}$ donde $a$ es el factor de escala de la misma que equivale a realizar un giro de la espiral de centro el polo y ángulo $\theta_0$ sin más que expresar $a=b^{\theta_0}$ . Obviamente la posición de la imagen y su escala no introduce ningún cambio en la forma y en el análisis realizado, es un cambio de posición y giro de la espiral que la ajusta. Sólo es una simplificación para un trabajo funcional más simple. $$r=1,186^\theta$$ con un factor de crecimiento $$\frac{r_{\theta+2\pi}}{r_\theta}=1,186^{2\pi}=2,92...$$ y ángulo característico de $80,32º$. Estos valores son próximos al factor 3 indicado por Moseley y al ángulo $80º$ $ 5'$ dado por Thompson, pero podemos observar que la espiral logarítmica correspondiente a este factor, cuya base cumpliría que $b^{2\pi}=3$, es decir, $b=1,191...$ se ajusta peor que la espiral detectada por Ildefonso y sus colegas (ver ). El ajuste global aplicado aquí mejora al local realizado en su momento. Este es un primer logro de esta investigación.
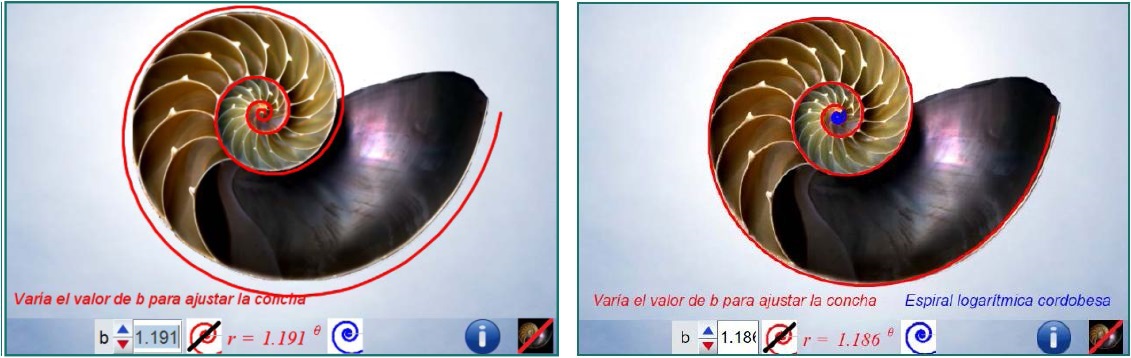
Y lo que es obvio es que esos valores eran muy diferentes de los valores de la espiral logarítmica áurea cuya ecuación es $$r=1,358456...^\theta$$ con factor de crecimiento $1,358456...^{2\pi}=6,854...$ y ángulo característico de $72,97º$ (ver ).
Obviamente el Nautilus ni era, ni es áureo, algo conocido por cualquier instruido en este tema, pero como se indica en el resumen del artículo que es objeto de análisis aquí (ver ) parece que lo bello y perfecto ha de ser áureo y si no, ha de posicionarse en una categoría inferior, tanto que muchos doctos transmiten de manera subeptricia la idea errónea de la divinidad nautilianaLa proporción áurea, extrema y media razón euclidiana, fue denominada por Luca Pacioli proporción divina en su libro "Divina Proportione" donde aportó hasta trece propiedades que la caracterizan. Entre ellas realizó semejanzas con Dios e indicó efectos no naturales sino divinos y en la decimotercera propiedad detuvo su descripción por reverencia a Nuestro Salvador Jesucristo y sus doce apóstoles, tratando de evitar poder condenarse. y de ahí el mito mal transmitido y divulgado. Pero no, el Nautilus no es áureo, no, no es divino.
Entonces, ¿habría que definir una proporción nautiliana caracterizada por el Nautilus, encuadrándolo en otro canon? ¡No sería mal motivo para dignificar a tan bello ejemplar! Y en ese objetivo pusieron empeño los tres investigadores.
Pero antes, quizás, habría que indicar por qué la espiral logarítmica áurea se llama así y cómo se puede asociar toda espiral logarítmica a una proporción. Detengámonos un instante en ello.
Antes hemos indicado que toda espiral logarítmica es equiangular, es decir, el ángulo que forma el radio vector de cualquier punto con la recta tangente en él es siempre constante. De hecho, Descartes fue quien quiso generalizar la propiedad de la circunferencia donde el radio y la recta tangente en todo punto es constante e igual a 90º y se planteó cuál sería la curva que cumpliera esa propiedad, pero para un ángulo dado cualquiera. Jakob Bernoulli también la estudió y la denominó "Spira mirabilis” o espiral maravillosa. Esa curva es la espiral logarítmica. Para profundizar en el conocimiento de esta familia de curvas y sus propiedades puede consultarse el artículo "El grillo y la espiral logarítmica" y la miscelánea que se enlaza en él.
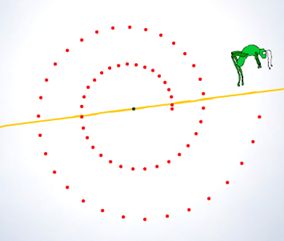
Por ser equiangular las rectas tangentes de cualquier cuarteto de puntos consecutivos que difieren $\frac{\pi}{2}$ radianes, en cordenadas polares, determinan un rectángulo y todos esos rectángulos tienen la misma proporción. Esa proporción es la proporción característica de cada espiral logarítmica y queda determinada unívocamente por ella.
Gráficamente significa que si quisieramos enmarcar un arco de espiral logarítmica en un rectángulo, el que se ajustaría de manera tangencial, el que mejor se ajustaría, sería el rectángulo que tuviera como proporción la característica de esa espiralPueden encontrarse artículos donde se le asigna a las espiral del Nautilus otras proporciones donde, cómo no, interviene el número áureo $\Phi$ en concreto $\frac{1}{\sqrt{\Phi}}$. Todo es fruto, consecuencia errónea, de enmarcarla en rectángulos que no son tangenciales a la espiral. . Esta proporción se demuestra que coincide con el cociente de las longitudes de cualquier pareja de radios vectores que se diferencian en $\frac{\pi}{2}$ radianes, es decir,
$$\frac{r_{\theta+\frac{\pi}{2}}}{r_\theta}=b^{\frac{\pi}{2}}$$ y se denomina pulsación cuadrantal (es el factor de crecimiento en cada cuarto de vuelta)También se utiliza la denominada pulsación diametral $\frac{r_{\theta+\pi}}{r_\theta}=b^{\pi}$ (factor de crecimiento cada media vuelta) y la radial que es el factor de crecimiento $\frac{r_{\theta+2\pi}}{r_\theta}=b^{2\pi}$ (cada vuelta)..
Todo lo especificado en esta sección puede observarse en el .
Si en el campo de texto $b$ de ese objeto ponemos el valor $1,358456...$ obtendremos que la proporción característica de esa espiral es $$1,358456...^{\frac{\pi}{2}}=1,618033...=\Phi$$
donde $\Phi=\frac{1+\sqrt{5}}{2}$ es el número áureo. De ahí que a esa espiral se le denomine espiral logarítmica áurea.
Y si ponemos el valor obtenido por nuestros colegas en el ajuste global que realizaron del Nautilus, es decir, $b=1,186$ obtenemos que la proporción asociada a esta espiral es: $$1,186^{\frac{\pi}{2}}=1,307...$$
Número que para quienes estaban trabajando con la proporción cordobesa contenía ¡un feliz parecido! ¡una feliz coincidencia!, pues el número cordobés es: $$\zeta=\frac{1}{\sqrt{2-\sqrt{2}}}=1,306562…$$
Por tanto, la espiral logarítmica cordobesa es aquella que cumple que $b^{\frac{\pi}{2}}=\zeta$, luego $b=1,185580...$, siendo su factor de crecimiento $$1,185580...^{2\pi}=\zeta^4=2,914214...$$ y ángulo característico (no describimos aquí su obtención) $80,32º$.
Con lo analizado en la sección anterior, Ildefonso y sus dos colegas, pudieron saltar al mundo matemático desde la yocto-yotta realidad en la que detectaron cuál era la espiral que globalmente se ajustaba a la sección de la concha del Nautilus y concluir que no era necesario definir ningún nuevo canon nautiliano porque el Nautilus se había decantado y ubicado desde hace tiempo en el canon cordobés, que estaba ligado a la proporción cordobesa, al número cordobés. La sección sagital de la concha del Nautilus se ajusta a una espiral cordobesa, el Nautilus es cordobés.
Éste es un segundo logro de la investigación. No obstante, más que logro, podría decirse que es una mera coincidencia, quizás banal. Pero hay coincidencias en las investigaciones que marcan a quienes investigan y alegran y motivan la continuidad de la investigación. Si se hubiera detectado otro valor tendría igual importancia, pero el que fuera en concreto aquél en el que habían estado trabajando, que no hubiera que inventarse un nuevo canon, sino que éste ya existiera, seguro que les dió mayor satisfacción. Y además si se juega con el hecho de que la proporción cordobesa se ha catalogado como humana, la dualidad se refuerza en este caso, pues después de haberse perseguido y promovido la divinidad del Nautilus, el que éste se muestre humano, de nuestro entorno vital, no deja de ser una paradoja graciosa.
Esa motivación les llevaría a conseguir los logros que podemos destacar como más importantes de este análisis, los relativos a la modelación de otros elementos característicos de la concha del Nautilus: el sifúnculo o canal sifuncular y los septos y las cámaras septales.
En el podemos determinar el coeficiente de retardo o factor de escala (etiquetado como "$a$" en la escena) de la espiral que
ajusta el canal sifuncular. El valor obtenido verifica aproximadamente $0,65 \le a \le 0,7$. Y si se considera que el sifúnculo es el eje medio del fragmacono, se obtiene el valor teórico $$a=\frac{1,185580...^{-2\pi}+1}{2}=0,6715...$$
De nuevo el Nautilus se mostraba cordobés, pues el sifúnculo es una espiral cordobesa En el interactivo, al pulsar sobre el botón con la espiral en color azul claro se activa un pulsador que permite visualizar una aproximación gnomónica discreta de paso $\frac{2\pi}{16}.$ apoyándose en los puntos del sifúnculo.. Y, en general todo punto de la sección sagital del fragmacono está situado en una espiral logarítmica cordobesa $$r=a b^\theta$$ $1,185580...^{-2\pi} \le a \le 1$, es decir, en el intervalo $0,3431... \le a \le 1$.
Ese ajuste del sifúnculo fue un tercer logro no citado, o al menos no visto con anterioridad, en la literatura sobre este tema.
Pero, aunque los avances en investigación se suelen presentar esquivos, pues el desconocimiento actúa como una lente que ciega o que aporta miopía o astigmatismo, también a veces suele acontecer que una vez alcanzado un avance aparecen otros más encadenados, dado que el conocimiento facilita la creación de nuevo conocimiento. Y esto les debió ocurrir, pues consiguieron modelar un elemento básico en la estructura de la concha del Nautilus, un elemento que le aporta la flotabilidad, nos referimos a los septos o tabiques de sepación, los arcos calcáreos ocultos que aportan tanta belleza y atractivo a todo aquel que ve en algún momento la sección del Nautilus.
En el disponemos de las herramientas suficientes para reproducir el trabajo realizado por Ildefonso, Ángel y José encaminado a la modelación de los arcos septales. Le invitamos a hacerlo. Para ello dispone:
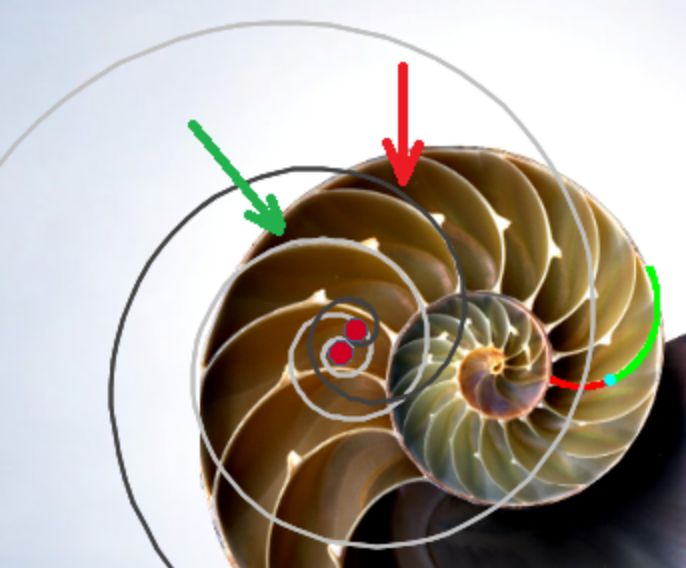
Así pues, consiguieron un cuarto y un quinto logro en la modelación de la concha nautiliana: Los septos son arcos de espirales cordobesas y los polos de estas espirales son puntos de en una espiral cordobesa.
Y añadieron un sexto logro: Todo punto del fragmacono de la concha del Nautilus está determinado por dos espirales cordobesas, una longitudinal semejante a la del perfil de la concha y otra transversal semejante a la de un arco septal.
E indicaron y afinaron bastante más en este modelo... pero nosotros, aquí, vamos a parar porque de manera análoga a que Luca Paccioli no quiso poner en peligro su salvación al citar propiedades de la proporción divina, nosotros no queremos tampoco poner en peligro su atención en esta descripción cansándoles con detalles matemáticos más engorrosos. Aquellos interesados pueden profundizar en el artículo original y en las misceláneas "La espiral logarítmica y el crecimiento gnomónico" y "Sobre el crecimiento cordobés del Nautilus Pompilius".
Es obvio que Ildefonso y sus dos colegas y amigos, como ellos decían y en este libro ya hemos escrito, pusieron la atención suficiente y supieron oír lo que el Nautilus les susurraba:
¡Qué no soy áureo! ¡Qué soy Cordobés!
Imagen de portada del capítulo: La web personal de Ildefonso.
Vía Verde - Oropesa del Mar. Castellón. España (Foto: COMUNITAT VALENCIANA)
Ildefonso editó y mantuvo una web personal que alojó en los servidores del Ministerio de Educación español. Este organismo facilitó, en su momento, que el profesorado pudiera elaborar sus páginas web personales y las divulgara.
En la fecha que escribimos esta reseña, el día 8 de septiembre de 2023, dicha web está operativa tal y como la dejó Ildefonso. En ella hay recursos de diferentes tipos y formatos: textos, escenas de Descartes, construcciones de GeoGebra, presentaciones PowerPoint, hojas de cálculo, un aula virtual con actividades php, etc.
También en la web de la herramienta GeoGebra Ildefonso mantenía una página personal que con la misma fecha anterior está operativa y contiene doscientos recursos, algunos de estos recusos están direccionados desde la web personal citada en el párrafo anterior.
Desde RED Descartes queremos tratar de mantener su contenido, evitando que decisiones ajenasEl Ministerio de Educación hizo un intento de dejar de prestar este servicio e incluso anunció la supresión de los contenidos subidos a ese servidor, sin embargo la resistencia manifestada por el profesorado usuario logró que ello no ocurriese. Pero nunca se está ajeno a esa posible pérdida por decisiones que puedan tomarse en el futuro.
En la web de GeoGebra también hubo un momento en que la introducción de cambios técnicos y organizativos produjo la no visualización de recursos desarrollados en versiones anteriores de esta herramienta y la ubicación y localización de los recursos también cambió. Por ello todos los recursos de Ildefonso en su página web de GeoGebra y los enlaces que realizaba desde su web personal a ésta los hemos ubicado localmente en este libro interactivo, preservándolos de otros posibles cambios venideros.
a nuestra organización puedan dejarlas inaccesibles y para conseguir este objetivo las hemos trasladado a nuestro servidor y también todo lo que puede ubicarse localmente lo hemos incluido en este libroHemos de pedir disculpas por los errores que hayamos podido cometer en este proceso, pues son muchos los recursos y acciones técnicas realizadas para conseguirlo.
.
Todas las direcciones web que hemos enlazado en las dos páginas anteriores son externas a RED Descartes y son los enlaces originales de Ildefonso. Aquí, la hemos ubicado localmente en este libro en el directorio denominado iferna14.
A primera vista, esta página principal, puede interpretarse que es una página de prueba y de aprendizaje de instalación del servidor Apache en los sistemas informáticos del Ministerio y de enlace de contenidos dentro de él. Esta interpretación surge al ver que hay contenidos diversos, pero poco estructurados y únicamente aparece destacado un epígrafe "Taller" que al acceder a él sí se observa que tiene una estructura definida, además lo ubicó en un directorio "nw" que podría interpretarse quizás como "nueva web" y que contiene parte de los contenidos de la página inicial. Podría ser que este "Taller" fuera su futura página principal, pero que quedó pendiente de direccionar como la página de inicio.
De los contenidos que incluye esta página destacamos:
Otros enlaces son:
Como indicábamos antes, por el contenido descrito, la página recoge contenidos de proyectos y cursos y finaliza incluyendo fotos con un presentador html5, posiblemente de otra práctica de un curso con este tema. Adicionalmente indica que la página "está en proceso de creación..."
Esta página de la web personal de Ildefonso (ver imagen en la , donde al pie se enlaza la web original externa) la hemos ubicado localmente en el directorio iferna14/nw/ y en ella se recogen diversos contenidos estructurados en siete secciones:
En el capítulo sexto de este libro "El GeoGebrero" hemos descrito y enlazado localmente cincuenta recursos de un total de doscientos desarrollados por Ildefonso con GeoGebra. En esta sección hemos reproducido la web original de Ildefonso en GeoGebra y la hemos ubicado localmente en el directorio webGeoGebra enlazando los doscientos recursos localmente, pero aquí no vamos a profundizar en la descripción de los mismos.
Pulsando sobre la imagen de la accederá a la versión local de esta web y pulsando sobre cada una de las tarjetas lo hará a cada uno de los recursos.
Podrá observar que la mayoría de estos objetos también estan enlazados en la página personal de Ildefonso en el Ministerio.
Y "Mutatis mutandis" hemos alcanzado el objetivo que nos marcamos al iniciar la redacción de este libro interactivo. En esencia, aglutinar la obra de Ildefonso durante el periodo que colaboró con RED Descartes y así poder mitigar su partida, la de un amigo del que
aunque la vida murió,
nos dexó harto consuelo
su memoria.
Estrofa XL de las "Coplas a la muerte de su padre" de Jorge Manrique
Versión musical interpretada por Paco Ibañez
Sit tibi terra tevis, requiescat in pace.
