Subproyecto Misceláneas.

El subproyecto Misceláneas está de enhorabuena, que se recuerde, pocas veces, en tan poco tiempo, un grupo tan reducido de personas ha aportado tanta cantidad de objetos de tan elevada calidad y tan alto potencial educativo a cualquiera de los subproyectos de la Red Descartes. Y no es la intención desmerecer al resto, muy al contrario; si no la de dar merecida notificación de un hito tan memorable. La excepcionalidad se justifica a si misma nada más visualizar cualesquiera de las últimas escenas incorporadas al subproyecto, lo que ya ha sido posible gracias a las reseñas que tanto José R. Galo Sánchez como Ángel Cabezudo Bueno han expuesto recientemente en el apartado Últimos materiales del blog y al artículo que el primero de ellos acaba de publicar, también en este blog, donde justifica el proceso de creación, creando a su vez nuevas escenas relacionadas con el tema de proporcionar una ayuda inestimable a la capacidad de visualización de las transformaciones dinámicas en el espacio tridimensional. Por otro lado la buena salud del subproyecto también se debe a la infatigable tarea de adaptación de materiales obsoletos, al nuevo editor DescartesJS, de las profesoras Elena E. Álvarez Sáiz y María José García Cebrian, los profesores ya mencionados y otros/as que aunque no se indican están en la mente de todos los usuarios del portal. Relativo a las aportaciones más recientes caben destacar:

• De la profesora Rita Jiménez Igea, quien nos ha sorprendido con un nuevo diseño de las escenas, más funcional, interactivo, armonioso y desde luego con un potencial instructivo y didáctico encomiable, seleccionamos una muestra de sus aportaciones:
  • Geometría del triángulo I
  • Geometría del triángulo II. Cálculo de rectas y puntos notables
  • Juego de Notación Científica
  • Jugando con Matemáticas
  • Matemáticas y joyería: una aleación de lujo
  • Ejercicios de mezclas
  • Bancos. Interés simple y compuesto

De las que destacamos:

Matemáticas, joyería y mezclas. 

• Seleccionar parte de las aportaciones del profesor José R. Galo Sánchez al subproyecto Misceláneas o casi a cualquier otro subproyecto es una tarea ardua, así que seleccionaré cronológicamente las siete últimas aportaciones relacionadas con el desarrollo del cubo y de entre ellas destacaré las tres más recientes; no obstante quisiera aprovechar la ocasión para documentar la génesis de la creación de las siete últimas y extraordinarias aportaciones de nuestro presidente para dar valor al ejercicio de la colaboración entre socios a tenor de los frutos obtenidos.
  
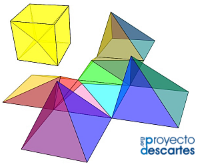
  En el año 2001 la profesora Ángela Nuñez Castaín publicó la miscelánea Partición de un cubo en seis pirámides triangulares iguales, en el año 2017 se adaptó a DescartesJS dicha miscelánea, la adaptación fué realizada conjuntamente por la profesora y nuestro presidente. A continuación se muestra el resultado obtenido.

  
  descomposición del cubo

  Las misceláneas más recientes que se han publicado sobre el tema han sido:
  • Partición de un cubo en pirámides de base cuadrada. Caso general.
  • Partición de un cubo en 4 pirámides cuadradas iguales dos a dos
  • Partición de un cubo en seis pirámides triangulares congruentes
  • Partición de un cubo en cinco pirámides triangulares
  • Partición de un cubo en seis pirámides cuadradas iguales
  • Partición de un cubo en cinco pirámides cuadradas
  • Partición de un cubo en tres pirámides cuadradas iguales
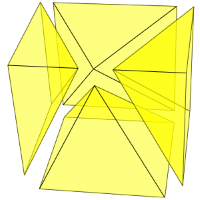
  • A la hora de cerrar este artículo nos vemos sorprendidos por una nueva y brillante aportación del profesor José R. Galo Sánchez que aunque aún no hemos tenido tiempo de analizar en profundidad consideramos de interés prioritario su exposición. Partición no prismática de un cubo en seis pirámides triangulares equivalentes
  
  De las anteriores destacamos:
  

  
  
  Descomposiciones del cubo

• A continuación, también a modo de resumen, exponemos tres misceláneas: la primera, que muestra la cuadratura de un polígono regular, elaborada por el profesor Ángel Cabezudo Bueno y el autor de este artículo y las otras dos, de este último, relativas a los patrones de teselación tipo mitad del cuadrado.
  • Pentágono regular: Cuadratura. Método clásico
  • Teselas del plano. Patrones: Mitad del cuadrado
  • Teselas del plano. Patrones: Mitad del cuadrado II
  
  

  
  
  Cuadraturas y Teselas

En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra una presentación de los cuerpos platónicos diferente a lo habitual.

Ildefonso Fernández Trujillo. 2018