Proporcionalidad. Espirales Aritméticas

Afortunadamente continúan las innovaciones en las posibilidades operativas y de uso de los materiales y Escenas de la Red Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS para intentar estar al día de las mismas, fundamentalmente a estos, que llevan a la información sobre cómo comunicar las escenas con el HTML y viceversa, y las escenas entre si y a estos otros que ilustran la manera de integrar el cálculo simbólico en las escenas.

También queremos animar a colaborar con los compañeros que están trabajando en el proyecto ed@d en moodle. El material que se está elaborando puede suponer una mejora extraordinaria en la labor educativa con un aumento significativo en la cantidad y calidad de la información expuesta y en la comunicación alumno-alumno, profesor-alumno y viceversa.

En este artículo nos vamos a centrar en la creación de una miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirá, estudiará y representará alguna de las siguientes espirales:  

• Espiral Aritmética o de Arquímedes
• Espirales arquimedianas. Envolventes Uniformes de: 2, 3, 4, ..., n centros. (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
• Espiral de litius
• Espiral de Fermat
• Espiral de Pitágoras (de Teodoro, de caracol...)
• Espilral de Ulam
• Espiral de Cornu
• Espiral de Durero
• Espiral de Fibonacci (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
• Espiral Hiperbólica (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
• Espiral Logarítmica (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
• Espiral de Parker (del viento solar)
• Espiral Cordobesa

Cada elemento de la lista anterior enlaza con una página que puede contener o enlazar a: la definición, la ecuación en polares, las ecuaciones paramétricas, la gráfica y otras características de cada espiral, por lo que la miscelánea que vamos a elaborar estará enfocada a mostrar el proceso de planificación y realización de dicha miscelánea teniendo en cuenta que los objetivos didácticos de cara al alumnado son: las aplicaciones de la proporcionalidad y el potencial de uso de las funciones trigonométricas elementales, logarítmicas y exponenciales.

Aprovecharemos este artículo, los siguientes y la miscelánea que elaboraremos, para la presentación de la espiral Cordobesa, particularización de las espirales gnomónicas y fruto de un largo y laborioso trabajo colaborativo, aún vigente, que nuestro compañero, Ángel Cabezudo Bueno, ha concretado, provisionalmente, con éxito.

No debe olvidarse que estamos estudiando una de las aplicaciones del concepto de Proporcionalidad siguiendo algunos de los materiales que están disponibles en el Proyecto Descartes y, eventualmente, algún otro contenido que por su indudable interés lo merezca.

LAS ESPIRALES ARITMÉTICAS

Al escenario donde va a desarrollarse la acción (E1) le hemos asignado unas dimensiones de 800x612 y dentro de este espacio general definiremos tres espacios rectangulares según muestra la siguiente imagen.

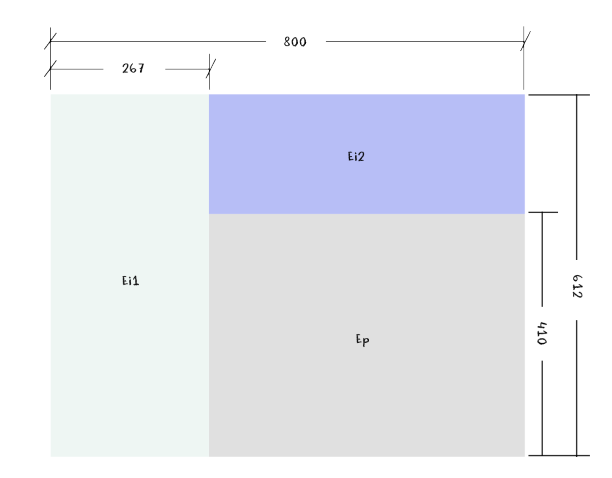
Los espacios Ei1 y Ei2 son, fundamentalmente, informativos aunque, eventualmente, pueden alojar algún elemento interactivo como un botón o un campo de texto. En el espacio Ep es donde se desarrollarán las acciones principales de la primera escena que está dedicada a la espiral Aritmética (de Arquímedes) y al grupo de espirales uniformes de 2, 3,...,n centros.

Comenzaremos trabajando de una forma peculiar, crearemos un solo espacio, el Ep, de dimensiones: 533x410 (conviene observar que 533 y 410 son, aproximadamente, el 67% de 800 y de 612 respectivamente) desarrollaremos todas las acciones de la primera escena que tienen lugar en este espacio con sus interrelaciones y, una vez finalizado este proceso, añadiremos los espacios Ei1 y Ei2, los dotaremos de contenido, y sincronizaremos la acción.

La base teórica de todo el trabajo para esta primera escena va a ser la observación de Arquímedes que originó la espiral que lleva su nombre:"Imaginaos una línea que gira con velocidad constante alrededor de un extremo, manteniéndose siempre en un mismo plano, y un punto que se mueve a lo largo de la línea con velocidad lineal constante: ese punto describirá una espiral"

Creamos el espacio Ep de 533x410 y en él vamos a representar lo descrito en la definición de tres maneras diferentes con objeto de practicar con las funciones seno y coseno y el concepto de proporcionalidad.

• Partiendo de dos segmentos horizontales superpuestos. Uno que gira a derechas y otro que gira a izquierdas.
• Partiendo de dos segmentos horizontales unidos por el punto fijo que giran en el sentido opuesto a las agujas del reloj.
• Partiendo de dos segmentos verticales superpuestos. Uno que gira a derechas y otro que gira a izquierdas.

Consideramos las dos opciones posibles de giro del segmento y algunas de las composiciones que seguramente son conocidas por todos pues son de uso habitual.
También, en esta primera escena, vamos a mostrar la construcción de las espirales uniformes de dos y tres centros lo que unido a las explicaciones informativas que se incluirán en su momento bastará para aprender a construir una espiral uniforme de cualquier número de centros. Esto hace que para mantener el carácter didáctico del código convenga añadir un nuevo espacio, que superpuesto al anterior se hará visible cuando el primero esté oculto.
Para conseguir lo expuesto necesitaremos definir algunos controles de distinto tipo, algún vector, varias funciones, diversos algoritmos de cálculo y bastantes gráficos.

Vamos a mostrar lo que queremos conseguir y luego veremos, paso a paso como lo hemos realizado.

El siguiente vídeo muestra como se ha realizado la escena anterior.

En próximas entradas continuaremos con el paso a paso de la escena, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.

Respecto al trabajo de investigación sobre las espirales gnomónicas en general y sobre la Cordobesa, en particular, que se está desarrollando, queremos mostrar los siguientes avances y animar a aportar alguna ayuda en el proceso de generalización emprendido.

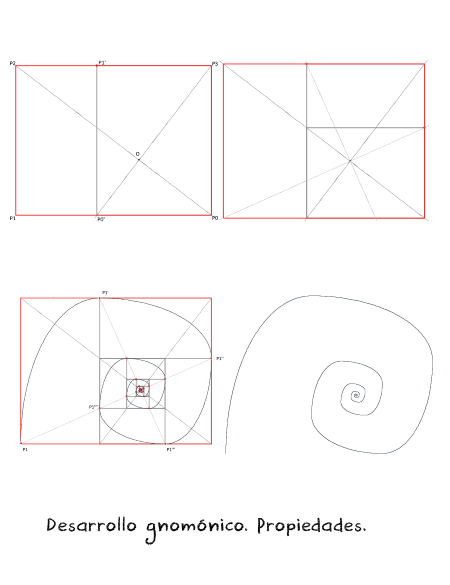
La siguiente escena muestra el avance realizado respecto a las iniciales.Espirales. Proceso de generalización

Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.

Ildefonso Fernández Trujillo