Misceláneas: Probabilidad. Inferencia.

Geometría y Probabilidad.

En los diferentes subproyectos que conforman la organización no gubernamental RED Descartes hay profusión de contenidos relativos a la Estadística y la Probabilidad que prácticamente cubren las exigencias curriculares de Primaria, ESO y Bachillerato. La particularidad de estos contenidos es que son: dinámicos, interactivos, formativos y en algunos casos, además, evaluativos. Ya en la anterior entrada en este blog señalamos algunos de esos recursos y siguiendo en esa línea y teniendo en cuenta que nuestro objetivo es el análisis de los errores de tipo I y II en los contrastes (tests) de hipótesis hemos seleccionado los siguientes contenidos:

• La Unidad Didáctica "El azar y la probabilidad." de la profesora Ángela Nuñez Castaín (2001) posteriormente adaptada a DescartesJS por ella misma y José R. Galo Sánchez (2017). La unidad es un primer acercamiento a los conceptos del azar y la probabilidad mediante ejemplos interactivos elementales ideales para conocer/recordar los fundamentos teóricos del estudio del azar.

  
  Carrera de coches controlada por dados.

 
• Si ya se conocen los fundamentos básicos de la Estadística y la Probabilidad el libro digital "Estadística, Combinatoria y Probabilidad" de Juan Jesús Cañas Escamilla y José R. Galo Sánchez, es la siguiente fuente de donde extraer la consolidación teórica rigurosa de los principios elementales y la justificación de los procesos operativos relacionados con los cálculos probabilísticos además de las técnicas organizativas de la información numérica en tablas y gráficos. Todo ello de forma gradual y apoyado en multitud de escenas interactivas de alto nivel educativo.

  
  Libro digital interactivo.

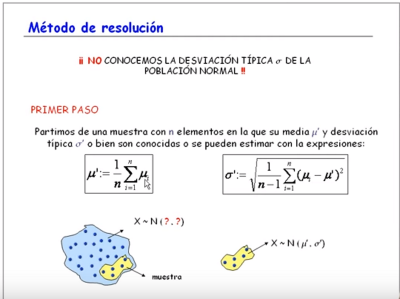
• En tercer lugar enlazamos el extraordinario libro digital interactivo "Estadística, Probabilidad e Inferencia", también de los autores Juan Jesús Cañas Escamilla y José R. Galo Sánchez, que hace un completo recorrido por los conceptos relativos a: la Estadística Unidimensional, Bidimensional, la Combinatoria, la Probabilidad, las variables estadísticas discretas y continuas y sus respectivas distribuciones de probabilidad y termina con un espléndido y documentadísimo análisis de la teoría del muestreo probabilístico y la inferencia estadística, todo ello acompañado de una batería de ejemplos, escenas interactivas, vídeos relativos a los contenidos y enlaces que hacen que el nivel de profundización en el estudio de la materia quede en manos de la persona interesada. Un ejemplo de escena interactiva, de las muchas que contiene el libro, es el que mostramos a continuación que apoya los conceptos teóricos de la introducción al estudio de los Intervalos de Confianza.
  
  

También enlazamos la excelente unidad didáctica, dinámica e interactiva, creada con DescartesJS por la profesora Mª José García Cebrian (2001) y revisada y adaptada por ella misma (2017)   INFERENCIA ESTADÍSTICA

Unidades Didácticas.

El problema de la aguja de Buffon - Laplace

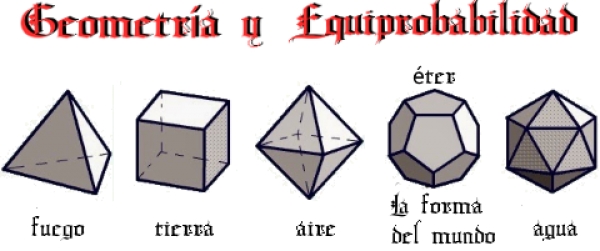
Desde la generalización del uso del astrágalo (taba) para dilucidar todo tipo de cuestiones relacionadas con la incertidumbre o sencillamente como elemento lúdico para ejercitar la habilidad mezclada con la suerte, la Geometría y el Azar comenzaron a ir de la mano. De hecho el gráfico de los cuerpos platónicos que mostramos en la cabecera de esta entrada es probablemente una de las mejores definiciones de equiprobabilidad que podamos ver. El hecho tangible de manipular cualquiera de estos cuerpos transmite una sensación de equilibrio, perfección y equidad, amén de otras, difícilmente igualable.

Los motivos por los que, primero el conde de Buffon y más tarde Pierre-Simón Laplace, conde del Imperio, atendieron este problema no están claros. El efecto inmediato si, a partir de entonces la utilidad del uso de la Geometría en cuestiones de probabilidad estaba comprobada así como el uso de métodos estadísticos y probabilísticos para aproximar valores de constantes geométricas.

Con el objetivo de rememorar el establecimiento formal de la relación entre la Estadística-Probabilidad con la Geometría y también por la idoneidad del experimento con la introducción al estudio de la Inferencia Estadística que estamos desarrollando se ha elaborado la miscelánea "Experimento: La Aguja de Buffon". En esta miscelánea se recrea dicho experimento con las siguientes particularidades:

• La escena simula el lanzamiento de 2 a 30000 agujas (o el lanzamiento de una aguja de 2 a 30000 veces).
• Cada lanzamiento de k agujas puede repetirse n veces así puede analizarse, en cada muestra, el comportamiento de los estadísticos estudiados, la influencia del tamaño de las muestras en el comportamiento de los estadísticos, el cumplimiento de  la ley de los grandes números y otros.
• Si el número de lanzamientos es menor o igual a 500 se representa cada una de las agujas lanzadas; si el número de agujas es mayor se muestra únicamente el punto medio de cada aguja.
• Con cada lanzamiento la escena expone un breve resumen de los resultados, así como el valor aproximado de π y la probabilidad de tocar línea en la muestra.
• El botón Indicaciones explica los objetivos y funcionalidad de la miscelánea.
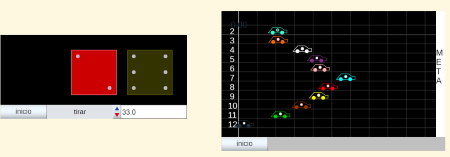
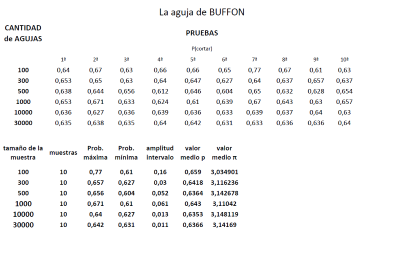
• La escena posibilita que en pocos minutos puedan realizarse experimentos como el que muestra el siguiente documento.

  
  

Experimento de Buffon. Lanzamiento de agujas.

En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra una clase sobre la estimación de la media poblacional mediante intervalos de confianza. Este vídeo es uno de los enlazados en el libro digital interactivo "Estadística, Probabilidad e Inferencia".

Acerca de los cuerpos platónicos.

• MATEMÁTICA Y FÍSICA EN EL TIMEO DE PLATÓN. POLIEDROS REGULARES Y ELEMENTOS NATURALES
• Los poliedros regulares y la esfera de: Javier Abia Llera (Adaptación a DescartesJS: José R. Galo Sánchez)
  • *"El dodecaedro es la forma que los dioses emplean para disponer las constelaciones en los cielos." Platón

  
  Unidades Didácticas. Materiales

Ildefonso Fernández Trujillo. 2018