Proporcionalidad. Las Espirales IX
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca el subproyecto TELESECUNDARIA.
En palabras del encargado de la presentación del subproyecto en el Blog, Ángel Cabezudo Bueno, "Telesecundaria es una modalidad de los estudios de educación secundaria en el Sistema Educativo de México dirigido a estudiantes adolescentes de 12 a 15 años que viven en comunidades dispersas que carecen de escuela de secundaria.
Se utilizan para ello los avances en tecnologías de la información y comunicación (TIC) como recurso para acercar esta formación a los jóvenes y puedan concluir su educación básica.
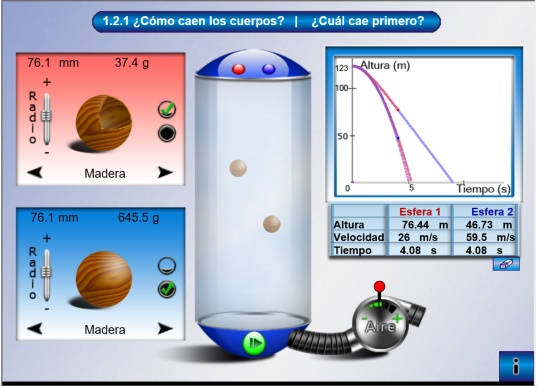
En este subproyecto de RED Descartes se han recogido objetos de la Telesecundaria desarrollando los correspondientes materiales con la herramienta Descartes. Las asociaciones de Colombia y España han sido las encargadas de preparar la adaptación a DescartesJS y en consecuencia todos podrán ser consultados en cualquier dispositivo con sistema operativo que admita un navegador compatible con HTML5." los primeros materiales pueden verse y descargarse siguiendo el enlace gráfico siguiente.
Dentro de nuestro ámbito local queremos destacar, entre otros, los siguiente materiales:
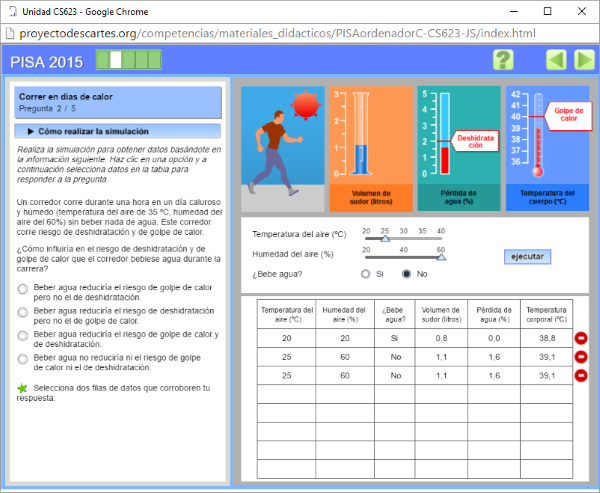
- Todos los creados para el subproyecto COMPETENCIAS. Debido a la creciente internacionalización de nuestro sistema educativo, progresiva integración en la comunidad europea, conviene que la manera de evaluar competencias en los ámbitos externos sea conocido con objeto de participar en igualdad de condiciones. Un acercamiento a estos procedimientos lo ofrecen los materiales del proyecto Competencias.
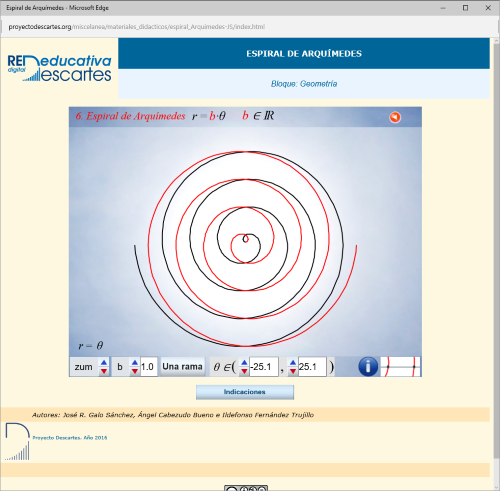
- La Miscelánea sobre la espiral de Arquímedes que sigue la corriente de mostrar los conceptos complicados, composición de movimientos, mediante la visualización del hecho de forma que es posible intervenir en la escena modificando los parámetros que la definen, con lo que la comprensión del concepto se facilita sobremanera, por lo tanto la miscelánea que se presenta es, por derecho propio, un objeto educativo lúdico e interactivo con un potencial formativo sobresaliente; no obstante en esta ocasión queremos enfocar el proceso de creación de la espiral desde el punto de vista de la definición de un lugar geométrico.
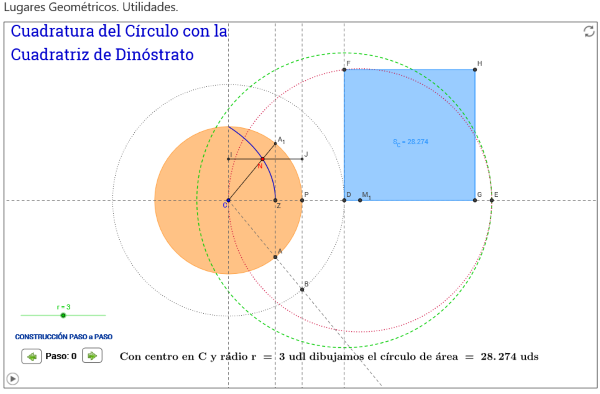
La miscelánea anterior muestra, paso a paso, la creación de un lugar geométrico (l.g.) por un punto que se mueve linealmente en un segmento mientras este gira alrededor de uno de sus extremos. Existen otros muchos lugares geométricos, entre los clásicos y más conocidos destaca la Trisectriz de Hipias que junto con la espiral de Arquímedes se ha usado, además de para otras utilidades, para la trisección de cualquier ángulo. A la Trisectriz de Hipias también se la llama Cuadratriz de Dinóstrato debido a que este geómetra usó el l.g. para la cuadratura del círculo. La Trisectriz (o Cuadratriz) es el l.g. generado por el punto común a dos segmentos uno de los cuales gira alrededor de uno de sus extremos y el otro se desplaza horizontalmente según muestran las siguientes escenas:
- La Trisectriz de Hipias que muestra, mediante una animación, la definición de la curva
- La trisección de un ángulo mediante la Trisectriz de Hipias. También se basa en una animación, en la primera parte se dibuja la curva y a continuación se muestra y explica, de forma dinámica, la trisección de un ángulo. La animación puede detenerse/reanudarse en cualquier instante.
- La cuadratura del círculo mediante la Cuadratriz de Dinóstrato (Primera Parte). Esta escena se basa en un pulsador que muestra, según se pulsa, la explicación del proceso para cuadrar el círculo. También tiene una animación que vuelve a construir la curva. La animación puede activarse/detenerse en cualquier instante.
Conviene analizar las escenas anteriores, reproducirlas y/o mejorarlas y ver la forma de integrarlas en la miscelánea sobre las espirales.
En próximas entradas en el Blog completaremos el estudio de uso de la Cuadratriz y veremos la manera de trisecar un ángulo y cuadrar el círculo con la espiral de Arquímedes.
En esta ocasión, en la sección de vídeo, hemos elegido uno muy particular que muestra la manera de dibujar la Trisectriz de Hipias (Cuadratriz de Dinóstrato) con ¿regla y compás? con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa. Buscando en internet se pone de manifiesto el enorme interés que suscitan, aún hoy en día, los problemas clásicos de la Geometría Griega.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Fermat" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral de Fermat
- Inclusión del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Y desde este enlace descargar el proyecto con la espiral de Fermat incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades hemos incluido dos trabajos, realizados con el programa GeoGebra, uno muestra el uso de la espiral de Arquímedes para la trisección de un ángulo y en el otro, enlazado en la imagen que sigue a la trisección, se lleva a cabo la cuadratura de un círculo de forma dinámica.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Bibliografía.- Para la realización de esta entrada y siguientes ha sido de gran ayuda la siguiente información:
- El trabajo sobre las TRISECTRICES de Pedro González Enríquez.
- Cuadratura de un círculo con la Cuadratriz de Dinóstrato
- Cuadratura de un círculo
Ildefonso Fernández Trujillo. Blog ReDescartes 2016



 CONTACTO
CONTACTO


