Lugares geométricos: Trisectriz de Maclaurin.

Continuamos con el estudio de los lugares geométricos y en esta entrada vamos a desarrollar una aproximación al conocimiento del l.g. conocido como "Trisectriz de Maclaurin". Este l.g. resuelve, en el siglo XVIII, el problema clásico de la trisección de un ángulo pero no como pretendían los antiguos sabios griegos; aunque sí de una forma muy elegante y funcional.

Para profundizar en el estudio del lugar geométrico y en el de uso del editor DescartesJS, hemos elaborado, de forma muy esquemática, las pequeñas utilidades que se muestran a lo largo del capítulo. Son escenas basadas en la obra del profesor Pedro González Enríquez, trabajo que está en proceso de adaptación a las nuevas versiones del editor DescartesJS.

La primera de las escenas genera la Trisectriz de Maclaurin de la siguiente manera:

• Establecido un sistema de referencia y considerada una distancia cualquiera, por ejemplo a = 1 se crean los siguientes elementos:
  • Con centro en el punto (4·a,0) y radio 4·a se traza una circunferencia.
  • Dibujar la recta vertical x = -2·a
  • Se considera un punto cualquiera, A, de la circunferencia. Este punto es importante pues hará posible la creación del lugar geométrico.
  • Trazar la cuerda que pasa por el origen de coordenadas y por el punto A. Esta cuerda cortará a la recta  x = -2·a  en un punto que hemos llamado B que variará según A se desplaza por la circunferencia.
  • Se considera el punto medio del segmento AB al que llamaremos C y que, solidario con la cuerda se desplaza por el plano. Este es el punto fundamental ya que es el que genera, en su desplazamiento, el l.g. en estudio.
• Cuando el punto A recorre la circunferencia, el punto C define la Trisectriz de Maclaurin
• Para observar la generación del l.g. basta con pulsar el botón "anima/para" de la escena.
• Conviene ver la generación del l.g. con la curva oculta.
• El botón "curva" oculta/muestra la gráfica de la curva:
  x·(x² + y²) = a·(3·x²-y²)   - ecuación cartesiana del l.g.

lugar geométrico

Para los lectores menos familiarizados con el proceso de creación de escenas DescartesJS indicamos que:

• Si se observan trazos o gráficas, generalmente de color rojo, no justificados, o se desea volver a ver la generación del l.g. es suficiente con pulsar el botón limpia, que quitará de la escena los trazos indeseados.
• El botón zum ajusta el tamaño de la parte visible. Este botón al ser activado limpia, de forma predeterminada, la escena.
• El pulsador a controla el tamaño del lazo de la trisectriz y el botón inicio reinicia la escena.

Como en anteriores ocasiones indicamos que la utilidad es fácilmente adaptable y admite las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.

La escena que exponemos a continuación muestra como el lazo de la trisectriz es en realidad un trisector de ángulos. Esto se evidencia de la siguiente forma:

• En esta ocasión el punto A, que pertenece al l.g., es un control gráfico que puede desplazarse por la parte superior de la curva. Conviene que este desplazamiento se haga lentamente para así observar la formación del ángulo principal BCA y su trisección COA (o COA').
• El vértice del ángulo principal es el punto C (2·a,0)
• El punto B (3·a,0) define con el C el lado CB de dicho ángulo principal. El otro lado del ángulo es el segmento CA o en su caso, A en el 2º cuadrante, CA'. La trisección del ángulo BCA es el ángulo COA (COA'). Observar la definición gráfica de los ángulos al desplazar el control A.
• Cuando el ángulo principal se aproxima a 180º la secante OA, o bien OA', tiende a ser la tangente del l.g. en 0⁺ que en este punto tiene de ecuación   y = 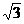x  por lo tanto la trisección de 180º es el ángulo que dicha tangente forma con la parte positiva del eje horizontal, esto es 60º.

Lazo trisectriz de Maclaurin.

En los siguientes trabajos presentamos una recreación de las escenas anteriores realizadas con el programa GeoGebra con los propósitos de ahondar en el conocimiento de ambas plataformas: GeoGebra y DescartesJS de forma paralela para lograr los objetivos señalados en entradas anteriores.

La siguiente utilidad genera la trisectriz al desplazar el punto A por la circunferencia.

creación del l.g.

En la siguiente escena se usa el lazo de la curva de Maclaurin como trisector de ángulos.

Lazo trisector de Maclaurin

Proponemos al lector el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.

En la sección de vídeo, hemos elegido uno que trata sobre lugares en el mundo conocidos, fundamentalmente, por sus características geométricas. El objetivo  es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Los Lugares Geométricos".

Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.

En próximas entradas continuaremos el estudio de los lugares geométricos y analizando el subproyecto Misceláneas.

Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.

Bibliografia:

• Parte de la Unidad creada por el profesor Pedro González Enríquez que se encuentra en fase de adaptación a DescartesJS.
• Caracol de Pascal
• Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
• Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
• La abundante información encontrada en la Wikipedia

Ildefonso Fernández Trujillo. 2017