Proporcionalidad. Las Espirales III

Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes caben destacar, entre otras, la creación del subproyecto Pisa con ordenador por parte de Mª José García Cebrian y José R. Galo Sánchez, documentado en este Blog por Santos Mondéjar López y la herramienta creada por el profesor Ángel Cabezudo Bueno que nos ha dotado de la posibilidad de analizar un crecimiento espiral y hallar la expresión matemática que mejor lo ajusta. La siguiente imagen enlaza con la miscelánea que explica el proceso de creación de dicha herramienta y el uso de la misma.

En el proceso de recuperación y adaptación de materiales de la Red Descartes que habían quedado obsoletos y en el de creación de nuevos recursos son varios los trabajos que merecen mención especial que ya está reflejada en el Blog, no obstante animamos a los socios y visitantes de nuestra web a usar y estudiar dichos trabajos y emprender tareas de adaptación-creación de: Unidades, Misceláneas, Discursos... para recuperar todo el esfuerzo e ilusión que en su día se invirtió y dotar a la aldea global de herramientas útiles para la enseñanza y el aprendizaje.

Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información de las funciones matemáticas disponibles para la construcción de escenas.

Antes de comenzar con el análisis de los gráficos incluidos en la escena en estudio vamos a mostrar un vídeo que relaciona los fractales y las espirales con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.

Los siguientes enlaces nos llevan a páginas donde puede ampliarse el conocimiento de las espirales y el concepto, significado y enfoque del estudio de las mismas.

• Espirales de Antonio Pérez Sanz
• Real Sociedad Matemática Española
• Espirales, fractales, Fibonacci,...
• Visión más espiritual
• Espirales y Laberintos

Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.  

En el artículo anterior nos quedamos estudiando los gráficos introducidos en la escena: puntos, segmentos, líneas, polígonos, textos... etc. Para lo cual abrimos la opción de menú Gráficos y observamos los 26 objetos creados y que muestra la siguiente imagen.

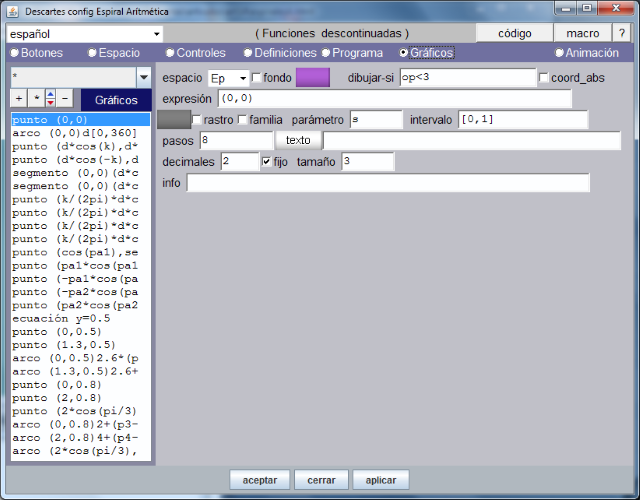
Insistimos en la conveniencia de descargar la escena, abrirla con el editor DescartesJS y analizar detenidamente las propiedades de cada gráfico. Si en este punto se tiene alguna duda el autor o la administración del Blog atenderán las consultas.

El código que corresponde a los gráficos se puede examinar y modificar, abriendo el archivo descargado "espiralesA.html", con un editor de texto plano. Las líneas que corresponden a dichos gráficos son las que comienzan por: <param name="G_x" que en nuestro caso llegan hasta <param name="G_26". Recordamos que se debe tener mucha precaución al editar directamente el código.

Observando la imagen vemos que, en primer lugar, se ha definido un punto en el origen de coordenadas (0,0) que, en esta ocasión, está centrado en la escena. Conviene, si no se tiene práctica, estudiar y probar las diferentes maneras de situar el origen de coordenadas de un espacio y el espacio en si mismo, dentro de la escena. También vemos el espacio donde se representará el punto, su color, tamaño y otra serie de parámetros autoexplicativos y de facil uso.
De los parámetros que ayudan a manejar un punto en la escena uno muy interesante es el de 'familia' que mediante un parámetro (variable) que se introduce en la/s coordenada/s y que se declara en el cuadro de texto "parámetro" (o se acepta el ofrecido por el editor 's') permite introducir simultáneamente tantos puntos como se precise en los lugares definidos por las coordenadas.
La siguiente imagen muestra como se han definido la colección de puntos azules que dibujan la espiral de Aquímedes según la definió el geómetra griego, donde se usa el parámetro global 'familia' con el parámetro o variable 'k '. Recordamos que en su momento definimos el control 'k ' y le asignamos un valor inicial y un valor final. Esta manera de proceder hace que la escena sea interactiva ya que el conrol k puede manipularse al estar presente en la escena en forma de pulsador.

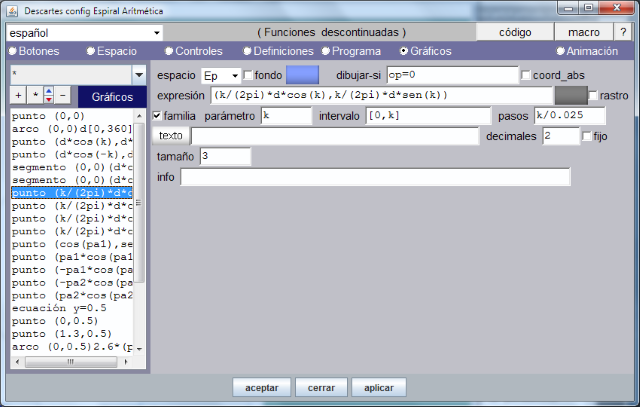
Puesto que disponemos de la escena podemos analizar cada uno de los gráficos cambiando los valores de sus parámetros y observando el efecto de las modificaciones para así aprender a configurar escenas con el editor de código.

Con objeto de practicar con los condicionales hemos elaborado la siguiente escena para su análisis. Es una pequeña aplicación donde se hace una breve introducción al estudio de la distribución de la proporción humana en superficies lisas mediante triángulos, rectángulos, rombos y otras figuras derivadas.

También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como obtener dos triángulos cordobeses a partir de un folio DIN A4.

Acceso al recurso en GeoGebra

En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral de Teodoro entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.

Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.

Ildefonso Fernández Trujillo