Proporcionalidad. Las Espirales II
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes cabe destacar el impresionante impulso que ha tenido el estudio generalizado de las espirales logarítmicas y la particularización al caso de las gnomónicas entre las que se han destacado las de proporción Divina y Humana. En esta línea el profesor Ángel Cabezudo Bueno ha dotado a la espiral humana de una nueva envoltura aproximándola gnomónicamente mediante funciones exponenciales. Estas son, con sus propias palabras, las razones que aporta para llevar a cabo la acción a la vez que ofrece unas instrucciones de uso de la escena que ha creado.
Espiral gnomon-exponencial y su correspondiente espiral logarítmica
Aparte de la proporción áurea o divina hemos venido trabajando con la proporción cordobesa por ser más natural o humana.
Nos llamó la atención la proporción cordobesa e investigamos de ella algunas cuestiones:
- ¿Cuál es su espiral obtenida al modo con que se obtiene la espiral de Durero en relación a la proporción Áurea?
- El gnomon áureo es un cuadrado y la espiral puede construirse fácilmente con regla y compás, pues basta dibujar un cuadrante de circunferencia haciendo centro en un vértice y conectando los dos vértices opuestos. Repitiendo este proceso sobre los sucesivos gnómones podemos obtener una versión muy aproximada de la espiral logarítmica correspondiente.
Queriendo hacer extensivo este procedimiento con el gnomon cordobés de lados desiguales nos fijamos en la elipse como curva que nos aproxima a la logarítmica correspondiente. El único inconveniente es que no se puede construir fácilmente, aunque sea de forma aproximada, con regla y compás. Además, piénsese que hay que dibujar cuatro arcos de elipse para cada vuelta de espiral. No obstante pudimos ver su dibujo utilizando DescartesJS, nuestra habitual herramienta matemática. - Otras espirales basadas en el modelo gnomon-elipse se han podido así mismo dibujar y aunque su estética no nos ha disgustado además de cumplir con la condición de ser derivables en los puntos de enlace de los arcos de elipse, hemos querido probar otras aproximaciones.
Pensando que el modelo gnomon-exponencial, que consiste en trazar arcos de exponencial en vez de arcos de elipse, debería de dar resultados mejores me he puesto a hacer unos cálculos y al ver que la cosa iba saliendo bien pasé a programar una escena con Descartes.
Debo advertir que esta escena ha estado orientada a hacer algunas averiguaciones en relación con este modelo gnomo-exponencial y hacer algunas comparaciones con lo que ya teníamos, es decir la construcción con el modelo gnomon-elipse y la espiral logarítmica. Por tanto he descuidado, en esta ocasión, la utilización de recursividad para obtener vértices y longitudes de los lados de los sucesivos gnómones dado que este problema ya lo tenemos resuelto (sendas escenas una del profesor José Galo Sánchez y otra mía) y queriendo ver enseguida resultados he trabajado con los valores de estos elementos en los cuatro primeros gnómones (de 0 a π/2, de π/2 a π , de π a 3π/2 y de 3π/2 a 2π), completando así una vuelta de espiral. Bien es cierto que han bastado estos cuatro gnómones para observar la recurrencia al calcular los parámetros de la exponencial en cada gnomon:
![]()
A esta, en coordenadas polares, que formalmente es la misma que la de la correspondiente espiral logarítmica, le aplicamos las condiciones de contorno al gnomon donde va a ser trazada. Es decir para un gnomon de lados a y b cuyo radio vector debe de rotar entre Θ y Θ+Π/2 le imponemos las siguientes dos condiciones:
- Para el ángulo Θ se debe cumplir que r = a
- Para el ángulo Θ+π/2, se debe cumplir que r = b
Con estas dos condiciones podemos determinar los parámetros m y n. Resulta que
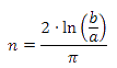
es una constante para todos los gnómones puesto que 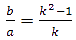 para cualesquiera a y b siendo k=razón de proporcionalidad (k=1,307 para la cordobesa, k=1,618 para la áurea, etc.)
para cualesquiera a y b siendo k=razón de proporcionalidad (k=1,307 para la cordobesa, k=1,618 para la áurea, etc.)
Los valores de m siguen esta ley de recurrencia: 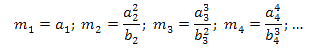 .......
.......
O bien teniendo en cuenta que 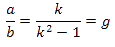 podemos escribir
podemos escribir![]() ........
........
La curva resultante es derivable en los puntos de empalme.
Un cambio de base c ≠ e en la exponencial es posible
r= m0·cn0·θ (2)
verificándose que ![]()
Para el caso k=1,618 (áurea), tenemos a = b (gnomon cuadrado) y la exponencial se convierte en circular pues ![]() con lo que la ecuación polar ahora es
con lo que la ecuación polar ahora es
r = m (3)
Con el modelo gnomon-elipse la traza circular era un caso de elipse y con el modelo gnomon-exponencial la traza circular es un caso de exponencial.
Veamos algunas imágenes captadas de la escena que nos permite hacer algunos comentarios y de paso explicar algo de la funcionalidad de la misma:
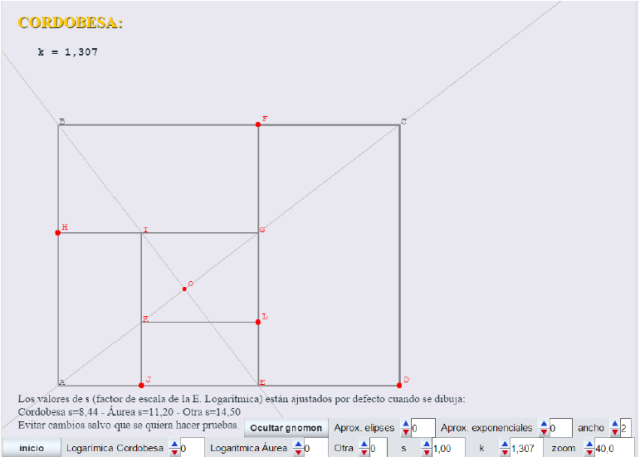
- EDCF (polo en E)
- GFBH (polo en G)
- IHAJ (polo en I)
- FJEL (polo en F)
-
-
- El control k proporciona sucesivamente K=1,307 (cordobesa), k=1,618 (áurea), k=1,929 (otra).
- Las correspondientes espirales logarítmicas a estos tres valores de k se obtienen poniendo a 1 su control que excluye al resto: Logarítmica Cordobesa, Logarítmica áurea y Otra logarítmica
- Se pueden representar para cierto valor de k, sus aproximadas espirales gnomónica-con-elipses y gnomónica-con-exponenciales.
- Las espirales para cierto k se pueden superponer para hacer comparaciones.
-
- Se representan sólo cuatro gnómones a partir del rectángulo ABCD:
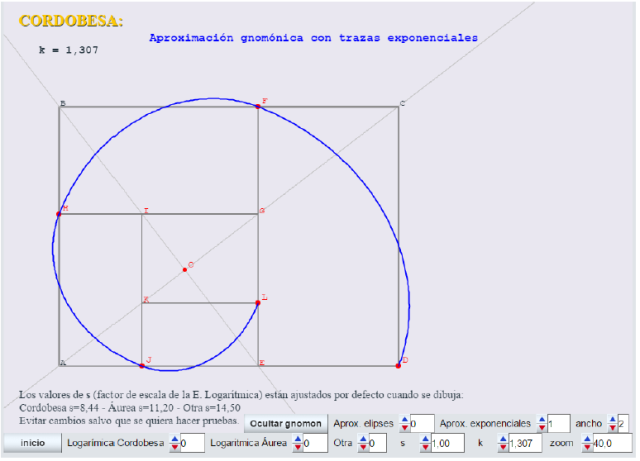
-
-
- El control ancho permite tres anchos de punto (1, 2, 3) de las curvas aproximadas. El ancho de la logarítmica es 1 fijo (se observa mejor la diferencia con ancho 1).
- El parámetro s es un factor de escala de la espiral logarítmica, que facilita el ajuste a los vértices de los gnómones. Están fijados por defecto para cada una de las tres espirales.
-
Observar la buena aproximación que se consigue con el modelo gnomon-exponencial para la cordobesa.
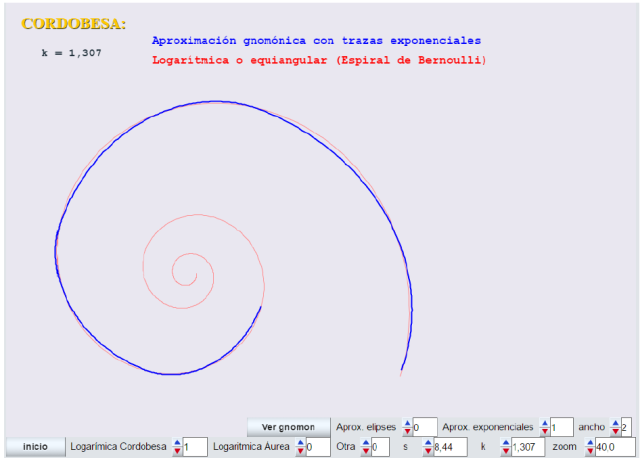
El modelo gnomon-elipse para valores de k menores que 1,618 (áurea) no es muy bueno. Este es el caso de la cordobesa.
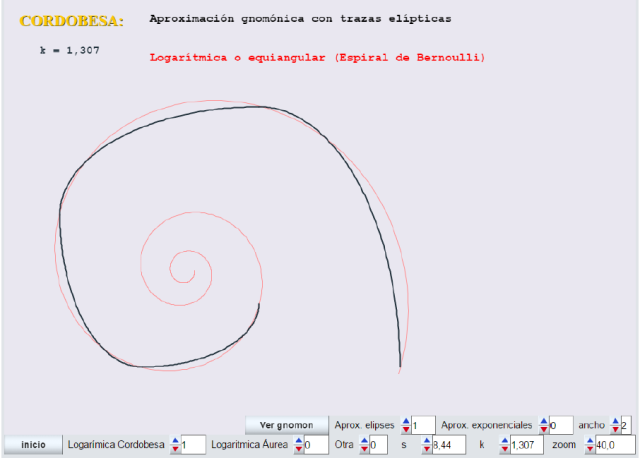
En la siguiente imagen podemos ver una comparativa de las tres espirales para el caso k=1,307 (cordobesa) al dibujarlas juntas.
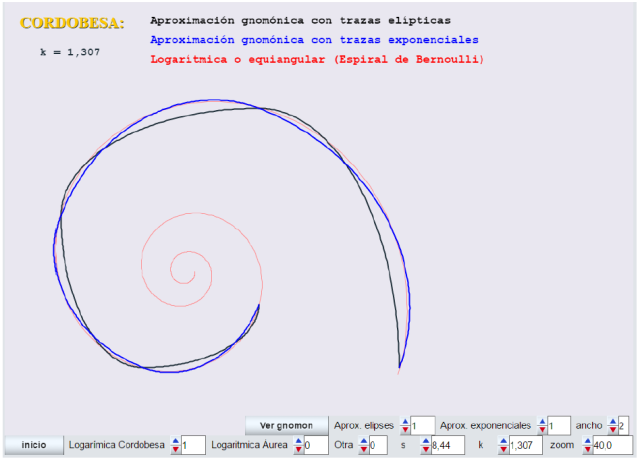
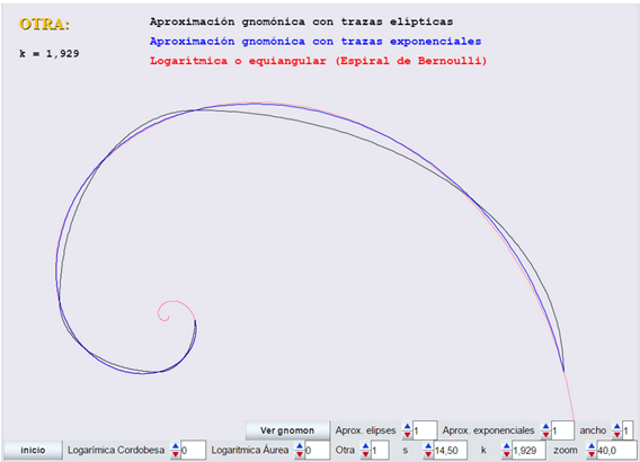
Ver el buen acoplamiento de las trazas exponenciales para k=1,929 (otra)
Animamos a colaborar con los compañeros que están trabajando en el proyecto ed@d en moodle. El material que están elaborando puede suponer una mejora extraordinaria en la labor educativa con un aumento significativo en la cantidad y calidad de la información expuesta y en la comunicación alumno-alumno, profesor-alumno y viceversa.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos que llevan a la información de cómo crear animaciones y juegos interactivos para el aula.
Antes de comenzar con el desarrollo de las aplicaciones de la Proporcionalidad vamos a mostrar el vídeo que el profesor Antonio Pérez Sanz elaboró para el programa + por - de TVE.
Los siguientes enlaces nos llevan a páginas donde puede ampliarse el conocimiento de las espirales y el concepto, significado y enfoque del estudio de las mismas.
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales:
Recordamos que la miscelánea que vamos a elaborar estará enfocada a mostrar el proceso de planificación y realización de dicha miscelánea teniendo en cuenta que los objetivos didácticos de cara al alumnado son: las aplicaciones de la proporcionalidad, el potencial de uso de las funciones trigonométricas elementales, logarítmicas y exponenciales, las ecuaciones paramétricas de una curva, la ecuación polar, las aplicaciones de la derivada y cualquier otro relacionado con el tema de estudio.
No debe olvidarse que estamos estudiando una de las aplicaciones del concepto de Proporcionalidad siguiendo algunos de los materiales que están disponibles en el Proyecto Descartes y, eventualmente, algún otro contenido que por su indudable interés lo merezca.
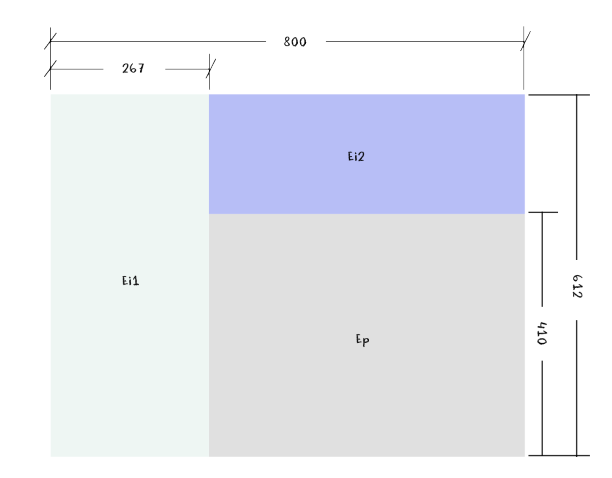
También recordamos que al escenario donde va a desarrollarse la acción (E1) le hemos asignado unas dimensiones de 800x612 y dentro de este espacio general definiremos tres espacios rectangulares según muestra la siguiente imagen.
En el artículo anterior se mostró la manera en que se había realizado la siguiente escena
hasta la creación, configuración y posicionamiento del control de tipo menú y de nombre "Espiral". La siguiente imágen muestra todos los controles necesarios para hacer que la escena funcione.
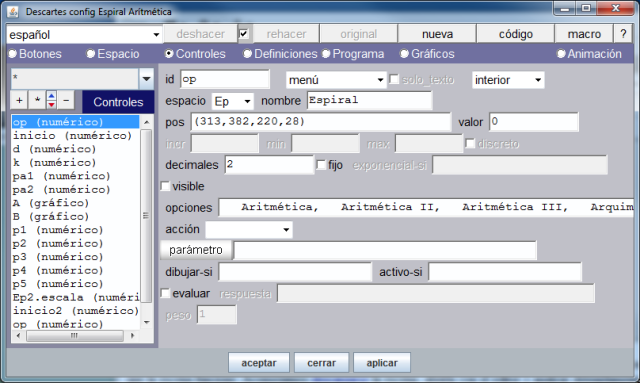
Aconsejamos descargar la escena, abrirla con el editor DescartesJS y analizar detenidamente las propiedades de cada control. Si en este punto se tiene alguna duda el autor o la administración del Blog atenderán las consultas.
El código que corresponde a los controles se puede examinar, y modificar, abriendo el archivo descargado "espiralesA.html", con un editor de texto plano. Las líneas que corresponden a dichos controles son las que comienzan por: <param name="C_x" que en nuestro caso llegan hasta <param name="C_16". Recordamos que se debe tener mucha precaución al editar directamente el código.
Ahora, seleccionando en el editor de código la opción Definiciones, observamos
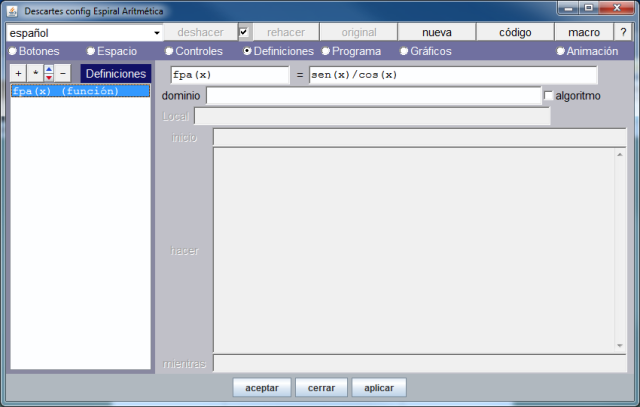
Se ha definido la función fpa que calcula la tengente de un ángulo dado en radianes para facilitar el dibujo de las familias de puntos.
En la opción Programa aún no se ha definido nada y en Gráficos se han definido varios puntos, segmentos etc... como puede comprobar el lector si abre dichas opciones de menú. En el próximo artículo explicaremos cada uno de los gráficos definidos.
Más adelante, cuando la primera fase esté completa, implementaremos los espacios informativos con los detalles de cada espiral y veremos la manera de sincronizar las distintas partes de la información.
Queremos adelantar, por si el lector desea hacer prácticas por su cuenta y luego comprobar los resultados, que una vez analizada la escena tal como está ahora, vamos a integrar en ella esta otra.
dedicada a la espiral de Teodoro

Pitágoras
En próximas entradas continuaremos con el paso a paso de la escena, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo


 CONTACTO
CONTACTO


