Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal
cuadratura del círculo - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II
- Páginas en GeoGebra de Vicente Martín Torres López
En particular la referente al Octógono regular
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Currículo para ESO y Bachillerato.
Ambos trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
- Estudio de la CUADRATURA I. La cuadratura del Octógono regular (método I).
A partir de un octógono regular de lado AB, controlable con el pulsador "lado" (ver imagen), calculamos el apotema a y área (paso = 0 de la escena) del mismo. En este paso es interesante observar la secuencia de ángulos que intervienen: π/8, π/4 y π/2. El resto de pasos de la escena están autojustificados y de ser precisa más información esta se encuentra en los pdf enlazados anteriormente y otros documentos de facil acceso en la red.
cuadratura del octógono
El método expuesto para la cuadratura del Octógono regular es el método estándar para cuadrar cualquier polígono regular. - Estudio de la CUADRATURA II. En esta ocasión descomponemos el octógono regular en cinco polígonos que lo recubren y con ellos formamos, a continuación, un cuadrado que, por lo tanto, es de igual área que el octógono.
Es trivial comprobar que lo dicho anteriormente es cierto basta con desplazar el pulsador k lentamente, a poder ser activandolo y usando las flechas de desplazamiento.
Cuadratura del Octógono II
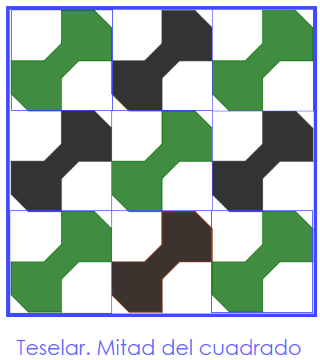
Enlazamos a continuación otros ejemplos de teselación relacionados con una razón o proporción o con el cuadrado.
teselas
Del tablero de ajedrez al hueso Nazarí. Transformación dinámica
teselas del cuadrado
Como en anteriores ocasiones notamos que las utilidades mostradas son fácilmente adaptables y admiten las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
Las siguientes imágenes enlazan con pequeñas herramientas realizadas con el programa GeoGebra en las que se recrean los procesos de generación de la Cuadratura del Octógono, primero por el método de descomposición en polígonos más pequeños con los que formar un cuadrado y a continuación por el método estándar o clásico.
Los trabajos siguientes son adaptaciones de otros muchos que hemos analizado en los materiales de la web de GeoGebra.
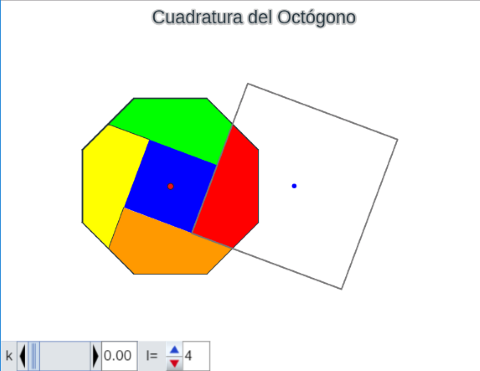
Cuadratura del Octógono. Método de descomposición.
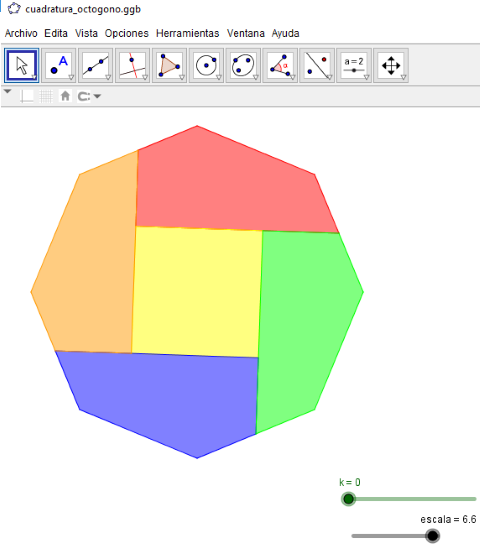
hoja de trabajo de la Cuadratura del Octógono (I)
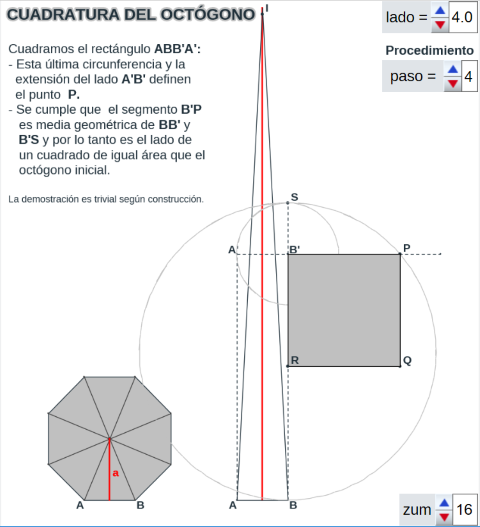
La siguiente imagen es el vínculo a la utilidad que muestra la generación de la Cuadratura del Octógono por el segundo método.
Cuadratura del Octógono. Método clásico.
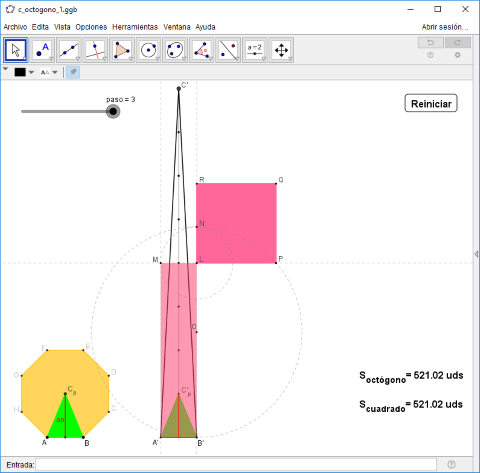
Cuadratura del Octógono (método II)
Proponemos el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido uno que muestra la deducción, paso a paso, de la cuadratura del círculo usando el número de oro. Conviene visualizar los tres vídeos que el autor dedica al tema. Como corolario deducimos la necesidad de dar a conocer, de forma divulgativa, la proporción humana o cordobesa.
La cuadratura del círculo
Continuando con la creación de la miscelánea "Las Espirales sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
CONTACTO
Código para embeber
