Proporcionalidad. Las Espirales IV

Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes y gracias al convenio de colaboración con la Facultad Regional Santa Fe de la Universidad Tecnológica Nacional de Argentina, está la miscelánea: Simulador de Sistemas diferenciales autónomos y no autónomos creada por la profesora Valeria Bertossi. La siguiente imagen enlaza con la miscelánea.

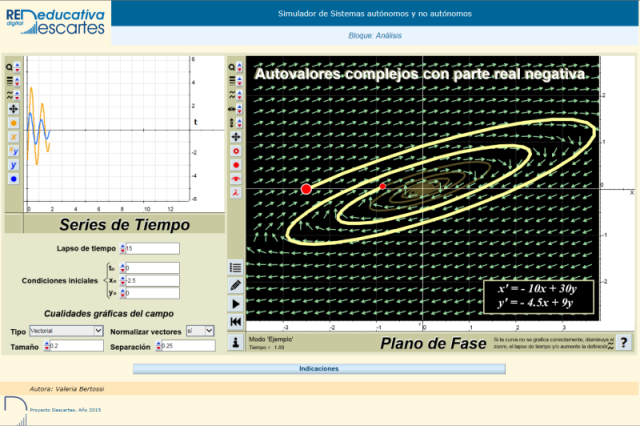
También cabe destacar la aportación del profesor José R. Galo Sánchez con su trabajo sobre Geometría tridimensional, también disponible en catalán gracias a la profesora Monserrat Gelis Bosch, que enlazamos a continuación.

En próximos artículos comentaremos y/o enlazaremos la espléndida colección de libros dinámicos, interactivos y multimedia del subproyecto iCartesiLibri que los profesores: Juan Jesús Cañas Escamilla, José R. Galo Sánchez, Juan Guillermo Rivera Berrío, Irma Manuela Benitez, Alicia Elena Carbonell y María Alicia Gemignani han creado sobre algunos temas de Estadística y Análisis. Por su indudable interés se aconseja visitar dicho subproyecto al igual que el recientemente elaborado por: José Luis Abreu León (Instituto de Matemáticas), Joel Espinosa Longi (Instituto de Matemáticas), Deyanira Monroy Zariñán (LITE) y equipo para Primaria, y que con el nombre @prende proporciona a los alumnos un material lúdico e interactivo que facilitará de forma notable la asimilación de conceptos matemáticos.

Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información sobre las familias 3D, elaborada por el profesor Juan Guillermo Rivera Berrío.

Antes de comenzar con el análisis de la escena de la espiral de Teodoro para incluirla en la miscelánea sobre las espirales en estudio, vamos a mostrar un vídeo que relaciona la música y las espirales con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.

Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.  

En el artículo anterior terminamos de estudiar el proyecto de miscelánea tal como está en la actualidad, indicando que íbamos a integrar en el mismo el contenido de la escena de la espiral de Teodoro.

La escena de la espiral de Teodoro, que vemos a continuación

Está formada por:

• dos controles tipo pulsador
• un texto
• un punto rojo de referencia
• una familia de 139 puntos
• otra de 138 segmentos.

Los pulsadores controlan, respectivamente, la cantidad de puntos y segmentos que están presentes en la escena. Inicialmente son visibles 0 segmentos y 29 puntos.
Con objeto de que puedan verse varias vueltas de la espiral, la escala del espacio donde se representa tiene un valor de 15 en lugar de 48 que es el que viene por defecto.
Para poder dibujar la colección de puntos, y posteriormente los respectivos segmentos, hemos definido:

• Un vector de 140 de tamaño para albergar los arcos que los segmentos que unen los sucesivos puntos con el de referencia forman con la horizontal.
• Una función, x1, para controlar la abscisa de los puntos.
• Otra función, y1, para controlar la ordenada de los puntos.

Los gráficos siguientes muestran como se ha hecho lo anterior.

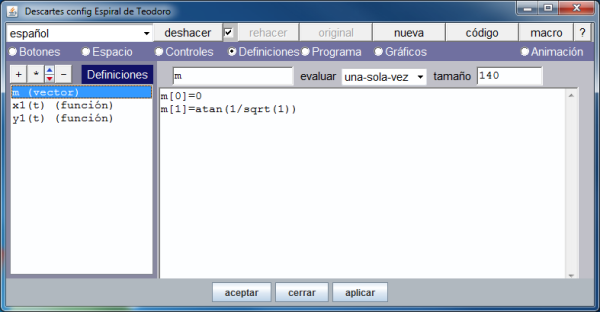
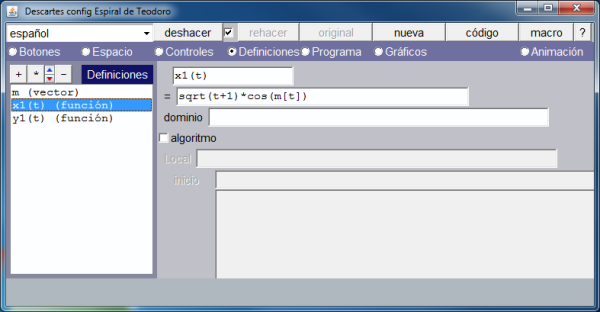
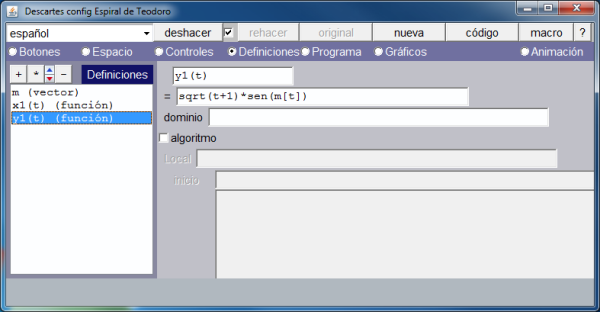
En la imagen que muestra la definición del vector se ve que únicamente se asignan valores a sus dos primeras componentes. Activando la opción de menú: Programa, vemos, en la siguiente imagen, como se han definido el resto de los arcos.

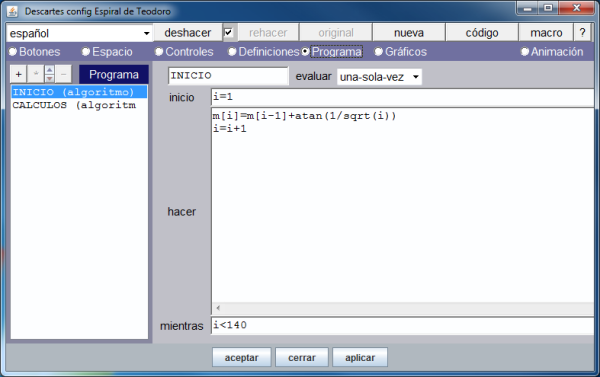
La siguiente imagen muestra los gráficos de la escena, en concreto despliega la forma en que se ha definido la colección de puntos.

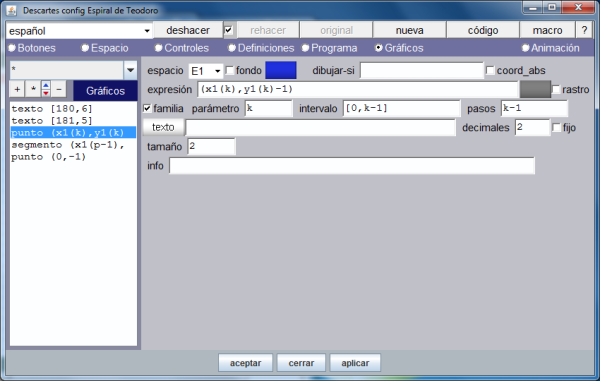
Observamos que los 139 puntos de la espiral se han definido mediante una familia que depende del parámetro k (identificador del pulsador de nombre: puntos presente en la pantalla).
La cantidad de puntos en pantalla depende del valor de este pulsador, el cual podemos manipular a nuestra conveniencia.

Analizada la escena de la espiral de Teodoro podemos pasar a incluirla en la miscelánea que estamos elaborando, acción que dejamos para el siguiente artículo. Aunque, insistimos, es conveniente que, para practicar con el editor de escenas, cada cual lo intente por su cuenta ya que disponiendo de las escenas se puede analizar cada uno de los cambios que se hagan y observar el efecto de cualquier modificación y así aprender a configurar escenas con el editor.

Como aplicación de la proporción Humana hemos elaborado la siguiente escena donde se hace una breve introducción al estudio del Triángulo Cordobés.

También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como teselar un cuadrado con triángulos cordobeses.

Acceso al recurso en GeoGebra


Conviene desplazar el deslizador tesela con las flechas del teclado.

En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral Cordobesa entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.

Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.

Ildefonso Fernández Trujillo