Proporcionalidad. Las Espirales X

Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades al subproyecto TELESECUNDARIA.

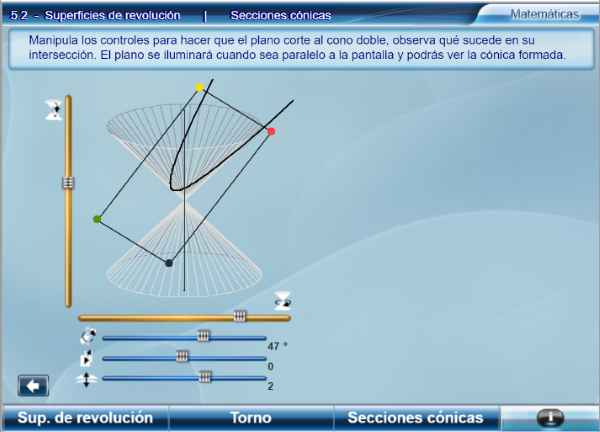
Como muestra, enlazamos la unidad sobre superficies de revolución

También es continuo el flujo de aportación de unidades al apartado GEOevaluación del subproyecto GEOgráfica

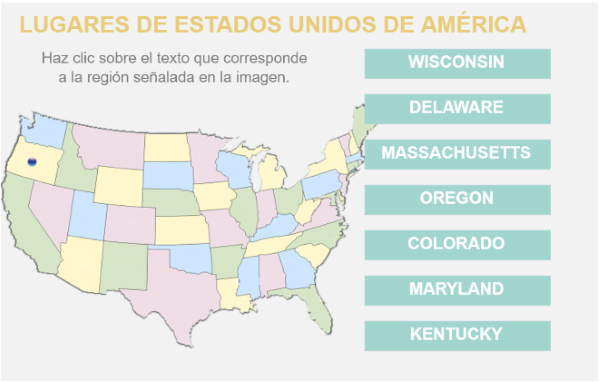
En esta ocasión enlazamos la Evaluación de los Estados Unidos de América

Dentro de nuestro ámbito local destacan, entre otras, las Misceláneas sobre las espirales, todas ellas de indudable valor en cuanto establecen un hito en el estudio de estos lugares geométricos aunque, en particular, es de especial interés la creada por Ángel Cabezudo Bueno ya que, además de ser la primera de la serie actual, entronca directamente con la fuente origen de dicha serie, el trabajo de José R. Galo Sanchez sobre las proporciones, la belleza en las Matemáticas y la espiral Cordobesa y es consecuencia de la acertada propuesta de espiral gnomónica Cordobesa, ambas: propuesta y miscelánea se muestran y/o enlazan a continuación.

El artículo anterior mostraba, paso a paso y exhaustivamente escenas interactivas con la creación de un lugar geométrico (l.g.) por un punto común a dos segmentos y por un punto que se mueve linealmente en un segmento mientras este gira alrededor de uno de sus extremos, el actual vuelve a construir la espiral de Arquímedes y también paso a paso e interactivamente muestra como trisecar un ángulo cualquiera y como hallar la cuadratura de cualquier círculo.

A continuación se exponen las escenas interactivas.

• Generación del lugar geométrico conocido como espiral de Arquímedes.
  

  
  
  

• Trisección de un ángulo mediante la espiral de Arquímedes.

  
  
  

• La cuadratura del círculo mediante la espiral de Arquímedes.

  
  
  

En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la relación de la espiral con la orografía y la interpretación de las señales cosmológicas por las diferentes culturas con objeto de apreciar distintas formas de enfocar el tema que nos ocupa.

Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral Hiperbólica" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:

• Hemos creado la siguiente escena: Espiral Hiperbólica

  
  
  

• Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto. Dejamos para los lectores interesados la inclusión total y/o personalizada de esta opción. 

La escena del proyecto puede verse a continuación:

Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Hiperbólica incluida.

También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades, hemos incluido los siguientes trabajos realizados con el programa GeoGebra: en el primero se muestra el uso de la espiral de Arquímedes para la trisección de un ángulo y en el segundo para la cuadratura del círculo.

En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.

Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.

Ildefonso Fernández Trujillo